
A major part of the planning of any investigation is the estimation of an appropriate sample size. In line with the move towards confidence intervals in data analysis, a number of sample size estimation methods based on that philosophy have been proposed as alternatives to the more traditional methods based on hypothesis testing. These newer methods just require a pre-specification of a target confidence interval width and are much easier to understand.
If the sole purpose of an investigation is to obtain an estimate for a non-comparative measure (for example, in a descriptive prevalence study where no comparisons are planned) then sample size calculations based on confidence interval width are perfectly acceptable. In this chapter, however I argue that for comparative studies, the confidence interval width approach, though appearing to have many advantages, leads to unacceptably small sample sizes. For such studies the traditional sample size formulae should always be employed. These formulae can, however, be made fully compatible with a confidence interval approach to data analysis with an appropriate change in the wording and interpretation of the specification.
The discussion is illustrated using the comparison of both means and percentages in two independent equal-sized groups using difference measures. The arguments, however, extend to unequal sample sizes, to the use of other measures (for example, ratios of means or relative risks) and to within-subjects designs such as crossover trials.
A large proportion of medical research involves the comparison of two groups, each of which may be considered a sample from a larger population in which we are interested. The hypothesis testing approach to statistical analysis determines if some appropriate comparative measure (such as a difference between means or percentages or a relative risk) is significantly different from its null value (for example a mean difference of zero or a relative risk of unity). The confidence interval approach, however, concentrates on an estimate of the comparative measure together with its confidence limits. The confidence interval gives an indication of the degree of imprecision of the sample value as an estimate of the population value. It is important to note that hypothesis testing and confidence intervals are intimately connected. If a 95% confidence interval does not include the null value of the hypothesis test then we can infer a statistically significant result at the two-sided 5% level. If the null value of the comparative measure lies inside the confidence interval then the result is not statistically significant (see chapter 3).
Suppose we are planning a randomised controlled trial to compare an antihypertensive agent with a placebo and that suitable hypertensive patients are to be randomised into two equal-sized groups. We take two cases. The first is where the treatment effect is to be evaluated by examining the difference in mean systolic blood pressure between the groups after a period of, say, six weeks. As an alternative endpoint, to illustrate the comparison of percentages, we also take the case where the treatment effect is evaluated by examining the difference in the percentage of patients in each group who have severe hypertension (say a systolic pressure above 180 mmHg).
To determine the sample size required for such a two group comparison several quantities must be considered:1,2
Table 12.1 Sample size in each group for an independent two-group comparison of mean blood pressures, pre-specifying power to detect a smallest worthwhile difference (at a two-sided significance level of 5%). The population standard deviation is 20 mmHg

Given levels for the significance, power and smallest difference (of means or percentages) to be detected and, as appropriate, a standard deviation or a percentage in controls, standard formulae, tables and graphs are available to enable calculation of the required sample size. These are reviewed by Lachin.2 To illustrate the method, Table 12.1 gives required sample sizes, in each group of our clinical trial, for three different levels of the smallest worthwhile difference in mean blood pressure to be detected (5, 10, and 15mmHg), and powers of 50%, 80%, and 90%. A two-sided 5% significance level, and a population blood pressure standard deviation of 20 mmHg are assumed. The required sample size increases with the power, but decreases for higher levels of the difference to be detected. For the same levels of power and significance, Table 12.2 gives sample sizes for detecting differences in the percentage with severe hypertension of 10%, 20% and 25% from a control level of 50%. The appendix gives the equations from which these figures are calculated.
Table 12.2 Sample size in each group for an independent two-group comparison of the percentage with severe hypertension, pre-specifying power to detect a smallest worthwhile difference (at a two-sided significance level of 5%). The percentage with severe hypertension in the controls is 50%

Most of the confidence interval approaches to sample size estimation are based on the expected width of the confidence interval for the comparative measure (difference between means or percentages) being analysed. (The width of a confidence interval is a measure of the imprecision of the sample estimate and is the difference between the upper and lower confidence limits. For example, if a confidence interval were determined to be from 90 to 170, its width would be 80.) All else being equal, the larger the sample size the narrower the width of the confidence interval. Once the width has been pre-specified, the only additional requirements for a sample size determination using this approach are the confidence level (95% or 99%) and an estimate of the variability of the means or an estimate of the percentages in the groups. These specifications are clinically understandable and the difficult concepts of power, the null value and a smallest difference to be detected seem to be avoided altogether. In addition, concentration on the precision of the estimate seems to fit in fully with an analysis that is to be performed using confidence intervals. Tables and formulae using this approach are available for various comparative measures in journals4–7 and textbooks.8 (A further refinement is to estimate sample sizes on the basis that the width of the confidence interval, rather than being fixed, is a percentage of the actual population value.4,5,9) Some simple formulae for sample size determination based on confidence interval width are given in the appendix.
Although the specifications of confidence level and confidence interval width for a sample size calculation are easy to understand, estimates of sample size based on this approach can be misleading. The consequences of employing such estimates do not seem to be clearly understood and in general the published work does not consider the problems explicitly. One distinction between hypothesis tests and confidence intervals is important in this regard.10,11 Hypothesis tests are essentially asymmetrical. Emphasis is on rejection or non-rejection of the null hypothesis based on how far the observed comparative measure (in our example, the difference between means or percentages) is from the value specified by the null hypothesis (a zero difference). On the other hand, confidence intervals are symmetrical and estimate the magnitude of the difference between two groups without giving any special importance to the null value of the former approach. It seems mistaken, however, to conclude that this null value is irrelevant to the interpretation of confidence intervals even though it plays no part in their calculation. Irrespective of precision, there is a qualitative difference between a confidence interval which includes the null value and one which does not include it. In the former case, at the given confidence level, the possibility of no difference must be accepted, while in the latter situation some difference has been demonstrated at a given level of probability. Herein lies the crux of the problem. In a comparative study can we ever say that the primary goal is just estimation and ignore completely the qualitative distinction between a “difference” and “no difference”, or in hypothesis testing terms, between a significant and a non-significant result? The answer is clearly “no” and I argue that the null value must have a central role in the estimation of sample sizes—even with a confidence interval approach—and that the position of the confidence interval is as relevant as its actual width.
The role of the smallest clinically worthwhile difference to be detected (as specified by the alternative hypothesis) has also been questioned in the context of sample sizes based on confidence intervals. Beal states: “With estimation as the primary goal, where construction of a confidence interval is the appropriate inferential procedure, the concept of an alternative hypothesis is inconsistent with the associated philosophy, even when used as an indirect approach to hypothesis testing. Thus one should not, in this situation, determine sample size by controlling the power at an appropriate alternative.”12 This viewpoint is untenable. For a sample size determination it seems inappropriate to specify the precision of an estimate without any consideration of what the real differences between the groups might be. Unfortunately, though the problem has been recognised by some,10,13 others make a correspondence between the precision of the confidence interval and the smallest difference to be detected. In the clinical trial example, we might decide that a confidence interval width for blood pressure difference of just under 10 mmHg would be sufficient to distinguish a mean difference of 5 mmHg from that of a zero difference. If the confidence interval were centred around the observed difference, the expected interval of 5 it 5 mmHg (that is, from 0 to 10 mmHg) would just exclude the null value. Similarly a confidence interval width of 20% for a difference between percentages should allow detection of a 10% difference.
Table 12.3 Sample size in each group for an independent two-group comparison of mean blood pressures, pre-specifying confidence interval width (95% confidence interval). The population standard deviation is 20 mmHg
| Confidence interval width | Sample size required |
| 5 mmHg | 123 |
| 10 mmHg | 31 |
| 15 mmHg | 14 |
Tables 12.3 and 12.4 give the sample size requirements in each group of our clinical trial to achieve confidence interval widths of 10, 20, or 30 mmHg for the difference in mean blood pressures between the groups, and to achieve confidence interval widths of 20%, 40%, and 50% for the difference in the percentage with severe hypertension. A comparison with the sample sizes based on the hypothesis test approach given in Tables 12.1 and 12.2 shows that those based on confidence intervals would have only 50% power to detect the corresponding smallest worthwhile differences. Thus even if the real difference were as large as postulated, with the confidence interval-based sample sizes there would be a 50% chance of the confidence interval overlapping zero. This would mean a statistically non-significant result and a consequent acceptance of the possibility of there being no real difference.
Table 12.4 Sample size in each group for an independent two-group comparison of the percentage with severe hypertension, pre-specifying confidence interval width (95% confidence interval). The table assumes that the width is equal to twice the difference between the population percentages, one of which is specified at 50%. See appendix
| Confidence interval width | Sample size required |
| 20% | 189 |
| 40% | 45 |
| 50% | 27 |
There are two reasons for this apparent anomaly. Take the comparison of means and assume the real population blood pressure difference was in fact 5 mmHg and that, based on a pre-specified confidence interval width of 10 mmHg, a sample size of 123 was used in each group. Firstly, this width is only an expected or average width. The width we might obtain on any actual data from the study would be above its expected value about 50% of the time. Thus, the confidence interval, if centred around 5 mmHg, would have a 50% chance of including zero. Secondly, the sample value of the blood pressure difference calculated on the study results would be as likely to be above the population value of 5 mmHg as below it. If our sample estimate were, for instance, 4 mmHg, then a confidence interval, with the expected width of 10 mmHg, would run from – 1 mmHg to +9 mmHg and would include zero difference as a possible true value. Thus specification of the expected width of a confidence interval as described above does not consider the possible true values of the difference and the power of detecting them (with a confidence interval excluding the null value of zero); nor does it consider what confidence interval width might actually be achieved. Consequently the approach leads to unacceptably small sample sizes with too low a power (only 50%) to detect the required effect.
Beal and Grieve propose sample size estimations based on a confidence interval width specification together with a probability (somewhat akin to power) that the width be less than a given value.12,14–16 This overcomes the problem related to expected width discussed above but does not account for the true location of the parameter of interest. Sample sizes based on this approach are still much lower than traditional estimates.
In planning any investigation, the question of power to detect the smallest clinically worthwhile difference must predominate over that of precision. In practice, of course, estimates based on samples large enough to detect small differences will have a high degree of precision. It is only when we are trying to detect large differences (not often found in medical research) that an imprecise estimate will result. In this latter situation it would in any case be possible to calculate a sample size based on precision also and use the larger of the two sizes so calculated. In line with this view, Bristol11 gives tables and formulae relating the width of the interval to the power for detecting various alternatives when comparing differences of means and proportions. However, if these factors have to be considered at all, why should sample size estimates not explicitly specify power to detect the smallest worthwhile difference in the first place, rather than concealing the specification in a vaguer requirement for confidence interval precision?
I propose that sample size requirements, which explicitly consider power, null values and smallest worthwhile differences, can easily be put into a confidence interval framework without the consideration of hypothesis tests in either design or analysis. Although the discussion has been in the context of employing the difference between means or percentages as a comparative measure, this proposal has general applicability. For calculation of a sample size based on a confidence interval approach we should specify (1) the confidence level (usually 95% or 99%), (2) the minimum size of the comparative measure we wish to estimate unambiguously (that is with the confidence interval excluding the null value), and (3) the chance of achieving this if the measure actually had this minimum value (in the population). These correspond, of course, to the traditional requirements of (1) the significance level, (2) the smallest worthwhile difference to be detected, and (3) the power of the study. Thus with only a slight change of wording the standard procedures based on hypothesis testing can be used to estimate sample sizes in the context of a confidence interval analysis.
In our example, we might have specified that the trial should be big enough to have an 80% chance that, if the real difference in blood pressure were 5 mmHg or greater, the 95% confidence interval for the mean difference would exclude zero. This would result in a sample size requirement of 251 in each group (see Table 12.1).
It is essential to note that this approach allows for the sampling variability of both the location and width of the confidence interval. The width of the interval, however, is not explicitly pre-specified. It is instead determined by the more important criterion that we are unlikely to miss a difference we wish to detect.
Greenland comes nearest to this view in terms of confidence intervals and sample size.10 The proposal outlined in this chapter is based on distinguishing between a particular difference, if it exists, and the null value. Greenland, however, in a subtle modification of this approach, also suggests that the sample size be large enough to distinguish between the null value and this difference, if the groups are in fact the same. In most situations this extra requirement does not result in an increase of sample size and it seems an unnecessary refinement.
There is no doubt that the whole topic of traditional sample size calculation tends to be complex and misunderstood and many studies are carried out with inadequate numbers.17,18 Estimating an appropriate sample size is a vital part of any research design and it is important that the current emphasis on using confidence intervals in analysis and presentation does not mislead researchers to employ sample sizes based on confidence interval width. Though apparently much simpler, such calculations can result in studies so small that they are unlikely to detect the very effects they are being designed to look for.
Examination of precision may well be a useful adjunct to the traditional estimation of sample size,13 but unless we place our primary emphasis on the question of power to detect an appropriate effect, we could be making a serious mistake. The use of confidence intervals in analysis, however, must be encouraged and this chapter has indicated how a realistic rewording of the usual specifications allows standard approaches to be used for sample size calculations in a confidence interval framework.
There is no need to throw out our old sample size tables in this era of confidence intervals. In fact we should guard them with care. Inadequate sample size has been a major problem in medical research in the past and we do not want to repeat those mistakes in the future. “However praiseworthy a study may be from other points of view, if the statistical aspects are substandard then the research will be unethical.”19 If we depart from the tried and tested approach for sample size calculations we are in danger of disregarding this principle.
This Appendix gives the formulae on which the sample size calculations in this chapter are based. Though percentages are used in the text the formulae given here, as in the rest of this book, are in terms of proportions. Significance, confidence and power levels are also expressed as proportions. All relevant quantities should be converted from percentages to proportions by dividing by 100 prior to using the formulae.
The following notation is employed:
| n | Sample size in each of the two groups (the value for n given by the formulae should be rounded up to the next highest integer) |
| σ | Population standard deviation (assumed equal in the two groups) |
| μ1, μ2 | Population means in each group |
| π1, π2 | Population proportions in each group |
| Δ | A Smallest worthwhile difference to be detected (μ1 – μ2 or π1 – π2) |
| α | Two-sided significance level |
| 1 – α | Confidence level |
| 1 – β | Power of test to detect the smallest worthwhile difference Δ |
| zk | 100kth percentile of Normal distribution |
Values of zk for values of k commonly used in sample size calculations are shown below:

The sample size per group, given a specification for significance, power and the smallest difference to be detected, is
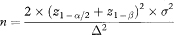
The expected 100(1 – α)% confidence interval for the difference between means (using the Normal approximation) is
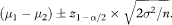
(Note that the actual confidence interval for a given set of study data would use the sample means rather than the population means, the pooled estimate of the sample standard deviation rather than σ, and the appropriate critical value of the Student’s t distribution rather than z1–α/2—see chapter 4.)
The expected width of the confidence interval, W, is thus
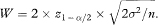
Rearranging this equation, the sample size per group, based on confidence interval width, is obtained as
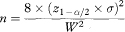
which, if W is set equal to 2Δ, reduces to
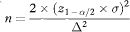
Sample size based on confidence interval width is thus equal to the conventional calculation when z1–β = 0, implying that β = 0·5 and the power is 50%.
The sample size per group, given a specification for significance, power and the smallest difference to be detected, is
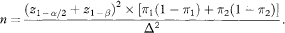
The expected 100(1 – α)% confidence interval for a difference between proportions (using the traditional method of chapter 6) is
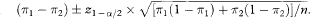
(Note that the actual confidence interval for a given set of study data would use the sample proportions rather than the population values. Also, chapter 6 presents more accurate formulae.)
The expected width of the confidence interval, W, is thus
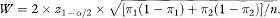
Rearranging this equation, the sample size per group, based on confidence interval width, is obtained as
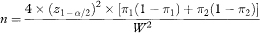
which, if W is set equal to 2Δ = 2(π1 – π2), reduces to
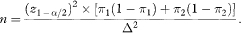
Sample size based on confidence interval width is thus equal to the conventional calculation when z1–β = 0, implying that β = 0·5 and the power is 50%.
1 Donner A. Approaches to sample size estimation in the design of clinical trials – a review. Stat Med 1984;3:199–214.
2 Lachin JM. Introduction to sample size determination and power analysis for clinical trials. Controlled Clin Trials 1981;2:93–113.
3 Spiegelhalter DJ, Freedman LS. A predictive approach to selecting the size of a clinical trial, based on subjective clinical opinion. Stat Med 1986;5:1–13.
4 McHugh RB, Le CT. Confidence estimation and the size of a clinical trial. Controlled Clin Trials 1984;5:157–63.
5 O’Neill RT. Sample sizes for estimation of the odds ratio in unmatched case-control studies. Am J Epidemiol 1984;120:145–53.
6 Day SJ. Clinical trial numbers and confidence intervals of pre-specified size (Letter). Lancet 1988;ii:1427.
7 Gordon I. Sample size estimation in occupational mortality studies with use of confidence interval theory. Am J Epidemiol 1987;125:158–62.
8 Machin D, Campbell MJ, Fayers PM, Pinol APY. Sample size tables for clinical studies. 2nd ed. Oxford: Blackwell Science, 1997.
9 Lemeshow S, Hosmer DW, Klar J. Sample size requirements for studies estimating odds ratios or relative risks. Stat Med 1988;7:759–64.
10 Greenland S. On sample-size and power calculations for studies using confidence intervals. Am J Epidemiol 1988;128:231–7.
11 Bristol DR. Sample sizes for constructing confidence intervals and testing hypotheses. Stat Med 1989;8:803–11.
12 Beal SL. Sample size determination for confidence intervals on the population mean and on the difference between two population means. Biometrics 1989;45:969–77.
13 Goodman SN, Berlin JA. The use of predicted confidence intervals when planning experiments and the misuse of power when interpreting results. Ann Intern Med 1994;121:200–6.
14 Beal SL. Response to “Confidence intervals and sample sizes”. Biometrics 1991;47:1602–3.
15 Grieve AP. Confidence intervals and trial sizes (Letter). Lancet. 1989;i:337.
16 Grieve AP. Confidence intervals and sample sizes. Biometrics 1991:47:1597–602.
17 Moher D, Dulberg CS, Wells GA. Statistical power, sample size, and their reporting in randomized controlled trials. JAMA 1994;272:122–4.
18 Thornley B, Adams C. Content and quality of 2000 controlled trials in schizophrenia over 50 years. BMJ 1998;317:1181–4.
19 Altman DG. Misuse of statistics is unethical. In: Gore SM, Altman DG. Statistics in practice. London: British Medical Association, 1982:1–2.