Chapters 4 to 11 contain formulae for calculating confidence intervals. Repeated use is made of the mathematical notation explained below.
 |
the mean of a sample of observations, where the individual observations are denoted by x or xi; it is pronounced “x bar”. In some chapters we use y and d to denote sets of observations and 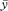 and and 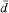 to denote their means. to denote their means. |
| p |
the proportion with a certain characteristic in a sample of individuals. |
| SD (or s) |
the standard deviation of a set of observations. It is a measure of their variability around the sample mean. s2 is known as the variance. |
| SE |
the standard error of the sample mean or some other estimated statistic. It is a measure of the uncertainty of such an estimate and is used to derive a confidence interval in most of the chapters in this book.
(The distinct uses and interpretation of the SD and SE are discussed in appendix 1 of chapter 3. Note that the notation SE(b) means “the standard error of b.”) |
| ∑ x |
the Greek capital letter sigma, denoting “sum of.” Thus ∑x means the sum of all the values of x. A more correct notation is 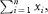 which means the sum of the n values of xi; that is, x1 + x2 + x3 + … + xn. The simpler notation ∑x is used when it is clear which items are being added together. which means the sum of the n values of xi; that is, x1 + x2 + x3 + … + xn. The simpler notation ∑x is used when it is clear which items are being added together. |
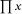 |
the Greek capital letter pi, denoting “product of.” Thus 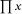 means the product of all the values of x. As with ∑x above, a fuller notation is means the product of all the values of x. As with ∑x above, a fuller notation is 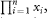 which is equal to x1 × x2 × x3 × … ×xn, but the shorter notation is used when the meaning is clear (see chapter 9). which is equal to x1 × x2 × x3 × … ×xn, but the shorter notation is used when the meaning is clear (see chapter 9). |
| (…) |
brackets are used in formulae to clarify the structure and to indicate the correct method of calculation. The quantity inside brackets must always be calculated first. If there are brackets within brackets the inner quantity is evaluated first. |
| logex |
the logarithmic function giving the value y such that x = ey, where e is the constant 2·718 281 … logex is sometimes known as the natural logarithm of x, and an alternative notation is ln x.
A key feature of the logarithmic transformation is that it is often successful in converting a non-Normal skewed distribution into an approximately Normal distribution (see chapter 4). Calculations, such as those to derive a confidence interval, can be performed using the log data and the results back transformed using the function ex (see next entry). |
| ex |
the exponential function denoting the inverse procedure to taking natural logarithms. It is sometimes called an antilogarithmic transformation. An alternative notation is exp(x). |
| n or N |
the sample size. |
| ni or Ni |
the sample size in the ith group of subjects. |
z1–α/2;
α;
100(1 – α) |
z1–α/2 represents a value from the “standard Normal distribution,” which is the theoretical Normal distribution with mean 0 and standard deviation 1 (see Figure 3.5). The subscript 1 – α/2 represents the proportion of the distribution below the value z1–α/2 Thus z0·975 is the value from the standard Normal distribution below which lies the bottom 0·975 (or 97·5%) of the distribution. For this example, α = 0·025 or 2·5%).
The central 1 – α, or 100(1 – α) %, of the distribution lies between zα/2 and z1–α/2. Because of the symmetry of the Normal distribution zα/2 = –z1 – α/2, so that the central 100(1 – α)% of the distribution lies between –z1–α/2 and z1–α/2.For example, the central 0·95 (or 95%) of the Normal distribution lies between –z0·975 and z0·975; that is, between –1·96 and +1·96. See also appendix 2 of chapter 3.
(Note that in the first edition we used the notation N1–α/2 rather than z1–α/2). |
| t1 – α/2 |
For some estimates, such as means and regression coefficients, the distribution of values from repeated sampling has a t distribution rather than a Normal distribution. For large samples the t distribution becomes nearly the same as the Normal distribution, but for small samples it has longer tails. As the tails of the distribution are relevant when calculating a confidence interval it is important to use the t distribution when appropriate. The logic behind the notation t1 – α/2, however, is exactly as for the Normal distribution described in the preceding entry.
The t distribution, and hence the value of t1 – α/2, is different according to the size of the sample(s) of data and is characterised by the “degrees of freedom”. The method for calculating the relevant degrees of freedom is given in those chapters which make use of the t distribution.
In many cases, both confidence intervals and hypothesis tests are calculated on the same data. It is important to remember that the value of the theoretical t distribution should be used for calculating a confidence interval, and not the observed value of the t statistic calculated in the hypothesis test. |
| P |
the probability value (or significance level) obtained from a hypothesis test. P is the probability of the data (or some more extreme data) arising by chance—that is, due to sampling variation only—when the null hypothesis is true. Hypothesis testing is discussed in chapters 3, 13, and 14, but methods are not covered in detail in this book. |

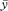 and
and 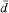 to denote their means.
to denote their means.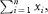 which means the sum of the n values of xi; that is, x1 + x2 + x3 + … + xn. The simpler notation ∑x is used when it is clear which items are being added together.
which means the sum of the n values of xi; that is, x1 + x2 + x3 + … + xn. The simpler notation ∑x is used when it is clear which items are being added together.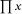
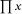 means the product of all the values of x. As with ∑x above, a fuller notation is
means the product of all the values of x. As with ∑x above, a fuller notation is 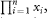 which is equal to x1 × x2 × x3 × … ×xn, but the shorter notation is used when the meaning is clear (see chapter 9).
which is equal to x1 × x2 × x3 × … ×xn, but the shorter notation is used when the meaning is clear (see chapter 9).