 of O2 gas.
of O2 gas.ammonia, ammonium nitrate, iron(III) chloride, calcium carbonate, and aluminum hydroxide.
Ammonia (NH3), ammonium nitrate (NH4NO3), iron(III) chloride (FeCl3), calcium carbonate (CaCO3), and aluminum hydroxide (Al(OH)3).
Do you know?
• The empirical formula (EF) of a compound is a representation of the simplest whole number ratio of the different atoms that made up the compound.
• The molecular formula (MF) of a compound is a representation of the actual whole number ratio of the different atoms that made up the compound. Thus, MF = n × EF, i.e., an empirical formula is a fraction of the molecular formula.
| Q | Is there any difference between the chemical formula of a covalent compound and an ionic compound? |
A: Certainly! The chemical formula of a simple molecular compound, such as H2O, tells us the number and type of elements present in a molecule. But for a macromolecular/giant covalent compound, such as SiO2, it is actually an empirical formula. It does not represent the actual number of atoms in the compound. As for an ionic compound, the chemical formula, such as KCl, is also an empirical formula, telling us the number of cations and anions present in one electrically neutral formula unit for the ionic compound.
(a) When the ozone molecule decomposes, it forms oxygen molecules. Give the balanced equation for this decomposition.
2O3(g) → 3O2(g).
| Q | Why must a chemical equation be balanced? Does this mean that all the reactants have completely been converted to the products in a balanced chemical equation? |
A: A balanced chemical equation does not mean that all the reactants have been converted to the products! Take for instance, two molecules of hydrogen gas (H2) react with one molecule of oxygen gas (O2) to produce two molecules of water (H2O):
2H2(g) + O2(g) → 2H2O(l).
If we have three molecules of H2 and only one molecule of O2, there would still be one molecule of H2 left unreacted. Why? Because the balanced equation tells us that! A chemical equation needs to be balanced simply because when matter reacts, the mass or amount of matter is the same before and after the reaction. You cannot destroy or create new matter and this is the basis for the Law of Conservation of Mass. But a balanced chemical equation does not guarantee that whatever you have put into the system would all react. Importantly, take note that matters react in specific proportions in accordance to the balanced chemical equation.
| Q | So, does it mean that O2 is the limiting reagent here? |
A: Yes, this would mean that O2 is the limiting reagent or H2 is the excess reagent. Hence, the actual amount of product, in this case H2O, is dependent on the actual amount of H2 that has reacted but not on the initial amount of H2 that is put into the system.
Do you know?
— Stoichiometry shows the relative quantities of reactants and products in a chemical reaction or the relative quantities of elements in a compound. In a balanced chemical reaction, which is represented by a balanced chemical equation, the relationship between quantities of reactants and products typically form a ratio of positive integral numbers. For example, two molecules of ozone gas (O3) decompose to produce three molecules of oxygen (O2).
— This particular kind of stoichiometry — describing the quantitative relationships among substances as they participate in chemical reactions — is known as reaction stoichiometry. Stoichiometric ratio of a reactant depicting the optimal ratio in which the reactant is needed for the complete reaction.
— For a compound such as H2O, the ratio of H:O = 2:1 is known as the composition stoichiometry. That is, it simply tells you how many atoms of each element are present in the compound. You can say that it is similar to the concept of molecular formula!
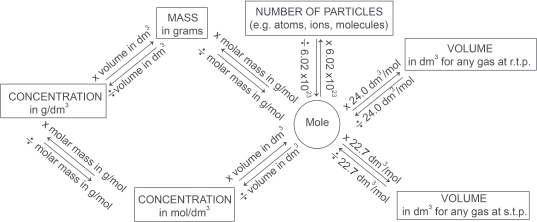
— The unit of measurement for the quantities of reactants or products in a chemical reaction is the mole. One mole of particles contains 6.022141 × 1023 mol−1 of particles.
(b) Calculate the volume of oxygen formed when 60 cm3 of ozone decompose at the same temperature and pressure.
According to the equation: 2O3(g) → 3O2(g), 60 cm3 of O3 would produce  of O2 gas.
of O2 gas.
| Q | In a balanced chemical equation, the coefficient in front of the chemical formula indicates the amount of particles in moles, so how can we simply calculate the volume of O2 just by using the volume of another gas? |
A: The basis behind the calculation of the volume of O2 gas is Avogadro’s Law, which states that: “equal volumes of all gases under the same conditions of temperature and pressure, contain the same number of molecules.” With this, for a chemical equation that involves only gas particles, the chemical equation gives the mole ratio as well as the volume ratio of the gaseous reactants and products.
Do you know?
— The molar volume of one mole of any gas occupies 24.0 dm3 at room temperature (20°C) and pressure (101,325 Pa or 1 atm) and 22.7 dm3 at standard temperature (0°C) and pressure (105 Pa or 1 bar).
| Q | Why is the molar volume of a gas smaller at a lower temperature? |
A: Easy! Remember that when temperature is lower, the kinetic energy of particles is lower? At a lower K.E., the particles move slower, thus the intermolecular forces between the particles would be able to pull the particles closer together, resulting in a contraction in volume.
| Q | Can we talk about molar volume for a liquid? |
A: No! This is because the intermolecular forces for different liquids vary in strength quite greatly. As a result, the “closeness” of the particles in the liquid state varies from liquid to liquid quite significantly. Unlike for gases, as long as the temperature and pressure are constant, the distance of separation between the gaseous particles do not vary too much.
| Q | So, the molar volumes for different types of gas are actually not the same? |
A: Yes, in fact there is a variation. If you are interested, you can refer to Understanding Advanced Physical Inorganic Chemistry by J. Tan and K.S. Chan for more details.
(c) Determine the amount of oxygen molecules in part (b) under s.t.p.
At s.t.p., one mole of gas occupies a volume of 22.7 dm3.
Hence, amount of oxygen molecules 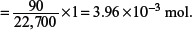
| Q | Can we write “mols” instead of “mol”? |
A: No! “Mol” is a unit for the amount of particles just like “kg” is the unit for mass. There is no plurality for units!
(d) Determine the volume of hydrogen gas that is needed to react with oxygen in part (c) if 4 cm3 of hydrogen reacts with 2 cm3 of oxygen. Give the balanced chemical equation based on the given information if the product formed is water.
If 4 cm3 of hydrogen reacts with 2 cm3 of oxygen, then 90 cm3 of oxygen would need:
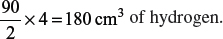
Since 4 cm3 of hydrogen contains twice the amount of particles than in 2 cm3 of oxygen, the balanced chemical equation is
2H2(g) + O2(g) → 2H2O(l).
3. Determine the mass of copper that can be obtained from 65.2 g of CuSO4·5H2O. Hence, determine the percentage by mass of oxygen in CuSO4·5H2O.
The molar mass of
CuSO4 · 5H2O = 63.5 + 32.1 + 4(16.0) + 5(18.0) = 249.6 g mol−1.
Amount of
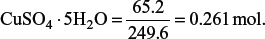
Since there are 0.261 mol of Cu in 0.261 mol of CuSO4·5H2O, the mass of copper that can be obtained = 0.261 × 63.5 = 16.6 g.
1 mol of CuSO4 · 5H2O contains 9 mol of oxygen atoms, hence the percentage by mass of oxygen in
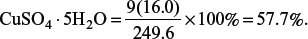
Do you know?
— Molar mass is the mass of one mole of a substance and is numerically equal to the relative atomic mass or the relative molecular mass of the substance expressed in grams. The unit for molar mass is g mol−1.
4. An unknown compound is found to have a molar mass of 194.19 g mol−1. From elemental analysis, its percentage composition by mass is found to contain: 49.48% C, 5.19% H, 28.85% N, and 16.48% O. Determine both the empirical and molecular formulae of the compound.

The empirical formula of the unknown compound is C4H5N2O.
Since molecular formula = n × empirical formula,
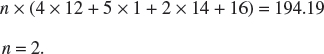
Hence, the molecular formula is C8H10N4O2.
BaCO3(s) + 2HNO3(aq) → CO2(g) + Ba(NO3)2(aq) + H2O(l).
In an experiment, 25.0 g of barium carbonate was completely reacted.
(a) Determine the amount of carbon dioxide evolved in terms of the number of moles and its mass.
Molar mass of BaCO3 = 137.3 + 12.0 + 3(16.0) = 197.3 g mol−1.
Amount of BaCO3 in 25.0 g 
One mole of BaCO3 gives one mole of CO2, hence the amount of CO2 evolved = 0.127 mol.
Molar mass of CO2 = 12.0 + 2(16.0) = 44.0 g mol−1.
Mass of CO2 = 0.127 × 44.0 = 5.59 g.
(b) What is the concentration of HNO3 that is needed if 50 cm3 of the acid were used to completely react with the barium carbonate?
One mole of BaCO3 reacts with two moles of HNO3, hence the amount of HNO3 used = 2 × 0.127 = 0.254 mol.
50 cm3 is equivalent to 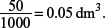
Concentration of 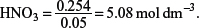
(c) What would be the concentration of sulfuric(VI) acid that is needed if only 32 cm3 of sulfuric acid were used?
The reaction equation between BaCO3 and H2SO4 is
BaCO3(s) + H2SO4(aq) → CO2(g) + BaSO4(s) + H2O(l).
One mole of BaCO3 reacts with one mole of H2SO4, hence the amount of H2SO4 used is 0.127 mol.
32 cm3 is equivalent to 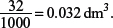
Concentration of 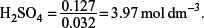
(d) Determine the mass of barium sulfate (BaSO4) that would be completely precipitated out by the sulfuric(VI) acid in part (c).
One mole of BaCO3 gives one mole of BaSO4, hence the amount of BaSO4 precipitated out is 0.127 mol.
Molar mass of BaSO4 = 137.3 + 32.1 + 4(16) = 233.4 g mol−1.
Mass of BaSO4 precipitated out = 0.127 × 233.4 = 29.6 g.
6. 5.77 g of white phosphorous and 5.77 g of oxygen were mixed and the following reaction to form phosphorous(III) oxide occurred:
P4(s) + 3O2(g) → P4O6(s).
In excess oxygen, the phosphorous(III) oxide can further react to produce phosphorous(V) oxide in accordance to the following equation:
P4O6(s) + 2O2(g) → P4O10(s).
(a) Determine which reactant is the limiting reagent. Hence, calculate the mass of P4O6 formed.
Amount of P4 in 
Amount of O2 in 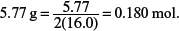
One mole of P4 reacts with three moles of O2; 4.65 × 10−2 mol of P4 would react with 3 × 4.65 × 10−2 = 0.1395 mol of O2.
P4 is the limiting reagent!
One mole of P4 gives one mole of P4O6; 4.65 × 10−2 mol of P4 would give 4.65 × 10−2 mol of P4O6.
Molar mass of P4O6 = 4(31.0) + 6(16.0) = 220.0 g mol−1.
Mass of P4O6 formed = 4.65x10−2 × 220.0 = 10.23 g.
Do you know?
— Phosphorous exists as simple discrete molecules, P4, and not in the monoatomic form.
(b) Determine the volume of oxygen at r.t.p. that is needed to convert the phosphorous(III) oxide to phosphorous(V) oxide.
One mole of P4O6 reacts with two moles of O2; 4.65 × 10−2 mol of P4O6 would react with 2 × 4.65 × 10−2 = 9.30 × 10−2 mol of O2.
At r.t.p., one mole of gas occupies volume of 24.0 dm3.
Hence, volume of O2 gas needed = 9.30 × 10−2 × 24.0 = 2.23 dm3.
(c) Calculate the mass of P4O10 that is produced.
One mole of P4O6 gives one mole of P4O10; 4.65 × 10−2 mol of P4O6 would give 4.65 × 10−2 P4O10.
Molar mass of P4O10 = 4(31.0) + 10(16.0) = 284.0 g mol−1.
Mass of P4O10 produced = 4.65 × 10−2 × 284.0 = 13.21 g.
P4O10(s) + 6H2O(l) → 4H3PO4(s).
Determine the number of moles of Ca(OH)2 that is needed to completely react with all the H3PO4 formed. Hence, calculate the concentration of the Ca(OH)2 solution that is needed if 50 cm3 of it was used, in both the mass and molar concentrations.
One mole of P4O10 gives four moles of H3PO4; 4.65 × 10−2 P4O10 would give 4 × 4.65 × 10−2 = 0.186 mol of H3PO4.
One mole of a tribasic acid would react with three moles of OH− ions to produce three moles of H2O.
Hence, two moles of H3PO4 would react with three moles of Ca(OH)2:
2H3PO4 + 3Ca(OH)2 → Ca3(PO4)2 + 6H2O.
Amount of Ca(OH)2 needed to react with 0.186 mol of
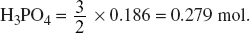
50 cm3 is equivalent to 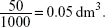
Concentration of Ca(OH) solution 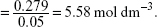
Molar mass of Ca(OH)2 = 40.1 + 2(16.0 + 1.0) = 74.1 g mol−1.
Concentration of Ca(OH)2 solution in g dm−3 = 5.58 × 74.1 = 413.5 g dm−3.