![]()
Although we’ll show you which mathematical concepts are most important to know for the SAT, this book relies on your knowledge of basic math concepts. If you’re a little rusty, this chapter is for you. Read on for a quick review of the math fundamentals you’ll need to know before you continue.
As you go through this book you might discover that you’re having trouble with stuff you thought you already knew—like fractions, or square roots. If this happens, it’s probably a good idea to review the fundamentals. That’s where this chapter comes in. Our drills and examples will refresh your memory if you’ve gotten rusty, but if you have serious difficulty with the following chapters, even after reviewing the material in this chapter, then you should consider getting extra help. For this purpose, we recommend our own Math Workout for the SAT, which is designed to give you a thorough review of all the fundamental math concepts that you’ll need to know on the SAT. Always keep in mind that the math tested on the SAT is different from the math taught in school. If you want to raise your score, don’t waste time studying math that ETS never tests.
Let’s talk first about what you should expect to see on the test.
Three of the nine scored sections on the SAT are Math sections. Two of the scored Math sections will last 25 minutes each; the third will last 20 minutes.
The math questions on your SAT will be drawn from the following four categories:
The math questions on your SAT will appear in two different formats:
Each of the three scored Math sections on your SAT will begin with the same set of instructions. We’ve reprinted these instructions, just as they appear on the SAT, in the Math sections of the practice tests in this book. These instructions include a few formulas and other information that you may need to know in order to answer some of the questions. You should learn these instructions ahead of time so you don’t have to waste valuable time referring to them during the test.
Still, if you do suddenly blank out on one of the formulas while taking the test, you can always refresh your memory by glancing back at the instructions. Be sure to familiarize yourself with them thoroughly ahead of time, so you’ll know which formulas are there.
Before moving on, you should be certain that you are familiar with some basic terms and concepts that you’ll need to know for the math sections of the SAT. This material isn’t at all difficult, but you must know it cold. If you don’t, you’ll waste valuable time on the test and lose points that you easily could have earned.
There are three rules regarding the multiplication of positive and negative numbers.
Integers are the numbers that most of us are accustomed to thinking of simply as “numbers.” Integers are numbers that have no fractional or decimal part. They can be either positive or negative. The positive integers are:
1, 2, 3, 4, 5, 6, 7, and so on
The negative integers are:
–1, –2, –3, –4, –5, –6, –7, and so on
Zero (0) is also an integer, but it is neither positive nor negative.
Note that positive integers get bigger as they move away from 0, while negative integers get smaller. In other words, 2 is bigger than 1, but –2 is smaller than –1. This number line should give you a clear idea of how negative numbers work.
![]()
You should also remember the types of numbers that are not integers. Here are some examples:
![]()
Basically, integers are numbers that have no fractions or decimals. So if you see a number with a fraction or non-zero decimal, it’s not an integer.
Even numbers are integers that can be divided by 2 leaving no remainder. Here are some examples of even numbers:
–4, –2, 0, 2, 4, 6, 8, 10, and so on
You can always tell at a glance whether a number is even: It is even if its final digit is even (divisible by 2). Thus 999,999,999,994 is an even number because 4, the final digit, is an even number.
Odd numbers are integers that have a remainder when divided by 2. Here are some examples of odd numbers:
–5, –3, –1, 1, 3, 5, 7, 9, and so on
You can always tell at a glance whether a number is odd: It is odd if its final digit is odd. Thus, 444,444,444,449 is an odd number because 9, the final digit, is an odd number.
Several rules always hold true with odd and even numbers:
even + even = even
odd + odd = even
even + odd = odd
even × even = even
odd × odd = odd
even × odd = even
You might see problems on the SAT that mention “distinct numbers.” Don’t let this throw you. All ETS means by distinct numbers is different numbers. For example, the set of numbers 2, 3, 4, and 5 is a set of distinct numbers, whereas 2, 2, 3, and 4 would not be a set of distinct numbers because 2 appears twice. Easy concept, tricky wording.
There are ten digits:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
All integers are made up of digits. In the integer 3,476, the digits are 3, 4, 7, and 6. Digits are to numbers as letters are to words.
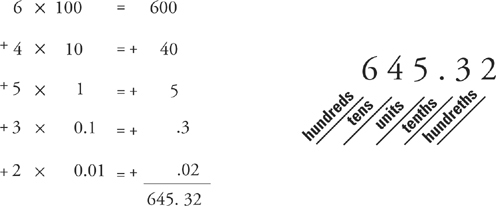
The integer 645 is called a “three-digit number” for obvious reasons. Each of its digits has a different name depending on its place in the number:
5 is called the units digit.
4 is
called the tens digit.
6 is called the
hundreds digit.
But what if we didn’t use an integer? If we had a number such as 645.32, which contains decimal places, we would know that it’s a little bit bigger than 645. Each decimal place tells us how much bigger.
3 is called the tenths digit.
2 is
called the hundredths digit.
Thus the value of any number depends on which digits are in which places. The number 645.32 could be rewritten as follows:
The factors of an integer are all of the integers that divide into it evenly. For example, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
A multiple of a number is any product of an integer and the given number. For example, 10, 20, 50, 180, and 370 are all multiples of 10. Make sure you know the difference between a factor and a multiple.
If an integer cannot be divided evenly by another number, the integer left over at the end of the division is called the remainder. Decimals cannot be remainders.
The best way to figure out a remainder is to actually do the long division. For example, if you want to find the remainder when 25 is divided by 3, set up and start solving a long division problem. Here’s what it would look like:
The 1 that is left over after you subtract the 24 is the remainder.
Consecutive integers are integers listed in increasing order of size without any integers missing in between. For example, –1, 0, 1, 2, 3, 4, and 5 are consecutive integers; 2, 4, 5, 7, and 8 are not. Nor are –1, –2, –3, and –4 consecutive integers, because they are decreasing in size.
A prime number is a positive integer that is divisible only by itself and by 1.
Here are a few important facts about prime numbers:
The following standard symbols are used frequently on the SAT:
| SYMBOL | MEANING |
| = | is equal to |
| ≠ | is not equal to |
| < | is less than |
| > | is greater than |
| ≤ | is less than or equal to |
| ≥ | is greater than or equal to |
There are only six arithmetic operations that you will ever need to perform on the SAT:
If you’re like most students, you probably haven’t paid much serious attention to these topics since junior high school. You’ll need to learn about them again if you want to do well on the SAT. By the time you take the test, using them should be automatic. All the arithmetic concepts are fairly basic, but you’ll have to know them cold. You’ll also have to know when and how to use your calculator, which will be quite helpful.
In this chapter, we’ll deal with each of these six topics.
You should know the following arithmetic terms:
Very often, solving an equation on the SAT will require you to perform several different operations, one after another. These operations must be performed in the proper order. In general, the problems are written in such a way that you won’t have trouble deciding what comes first. In cases in which you are uncertain, you need to remember only the following sentence:
Please Excuse
My Dear
Aunt Sally;
she limps
from left to right.
That’s PEMDAS, for short. It stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subtraction. First, you clear the parentheses; then you take care of the exponents; then you perform all multiplication and division at the same time, from left to right, followed by addition and subtraction, from left to right.
The following drill will help you learn the order in which to perform the six operations. First, set up the equations on paper. Then, use your calculator for the arithmetic. Make sure you perform the operations in the correct order.
Solve each of the following problems by performing the indicated operations in the proper order. Answers can be found here.
1. 107 + (109 – 107) = _____________
2. (7 × 5) + 3 = _____________
3. 6 – 3 (6 – 3) = _____________
4. 2 × [7 – (6 ÷ 3)] = _____________
5. 10 – (9 – 8 – 6) = _____________
Using parentheses to regroup information in SAT arithmetic problems can be very helpful. In order to do this, you need to understand a basic law that you have probably forgotten since the days when you last took arithmetic—the distributive law. You don’t need to remember the name of the law, but you do need to know how it works.
If you’re multiplying the sum of two numbers by a third number, you can multiply each number in your sum individually. This comes in handy when you have to multiply the sum of two variables.
If a problem gives you information in “factored form”—a (b + c)—then you should distribute the first variable before you do anything else. If you are given information that has already been distributed—(ab + ac)—then you should factor out the common term, putting the information back in factored form. Very often on the SAT, simply doing this will enable you to spot ETS’s answer.
For example:
Distributive: 6(53) + 6(47) = 6(53 + 47) = 6(100) = 600
Multiplication first: 6(53) + 6(47) = 318 + 282 = 600
You get the same answer each way, so why get involved with ugly arithmetic? If you use the distributive law for this problem, you don’t even need to use your calculator.
The drill on the following page illustrates the distributive law.
Rewrite each problem by either distributing or factoring, whichever is called for, then solve. Questions 3, 4, and 5 have no numbers in them; therefore, they can’t be solved with a calculator. Answers can be found here.
1. (6 × 57) + (6 × 13) = ____________
2. 51(48) + 51(50) + 51(52) = ________
3. a(b + c – d) = _____________
4. xy – xz = _____________
5. abc + xyc = _____________
The expression ![]() is
exactly the same thing as x ÷ y. The expression
is
exactly the same thing as x ÷ y. The expression
![]() means
nothing more than 1 ÷ 2. In the fraction
means
nothing more than 1 ÷ 2. In the fraction ![]() ,
x is known as the numerator (hereafter referred to as
“the top”) and y is known as the denominator (hereafter
referred to as “the bottom”).
,
x is known as the numerator (hereafter referred to as
“the top”) and y is known as the denominator (hereafter
referred to as “the bottom”).
To add two or more fractions that all have the same bottom, simply add up the tops and put the sum over the common bottom. For example:
![]()
Subtraction works exactly the same way:
![]()
In school you were taught to add and subtract fractions with different bottoms, or denominators, by finding a common bottom. To do this, you have to multiply each fraction by a number that makes all the bottoms the same. Most students find this process annoying.
Fortunately, we have an approach to adding and subtracting fractions with different bottoms that simplifies the entire process. Use the example below as a model. Just multiply in the direction of each arrow, and then either add or subtract across the top. Lastly, multiply across the bottom.
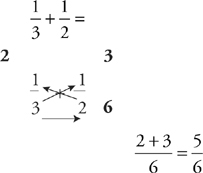
We call this procedure the Bowtie because the arrows make it look like a bowtie. Use the Bowtie to add or subtract any pair of fractions without thinking about the common bottom, just by following the steps above.
Multiplying fractions is easy. Just multiply across the top, then multiply across the bottom.
Here’s an example:
![]()
When you multiply fractions, all you are really doing is performing one multiplication problem on top of another.
You should never multiply two fractions before looking to see if you can reduce either or both. If you reduce first, your final answer will be in the form for which ETS is looking. Here’s another way to express this rule: Simplify before you multiply.
To divide one fraction by another, flip over (or invert) the second fraction and multiply. Doing this is extremely easy, as long as you remember how it works.
Here’s an example:
Be careful not to cancel or reduce until after you flip the second fraction. You can even do the same thing with fractions whose tops and/or bottoms are fractions. These problems look quite frightening but they’re actually easy if you keep your cool.

When you add or multiply fractions, you will very often end up with a big fraction that is hard to work with. You can almost always reduce such a fraction into one that is easier to handle.
To reduce a fraction, divide both the top and
the bottom by the largest number that is a factor of both. For
example, to reduce ![]() ,
divide both the top and the bottom by 12, which is the largest
number that is a factor of both. Dividing 12 by 12 yields 1;
dividing 60 by 12 yields 5. The reduced fraction is
,
divide both the top and the bottom by 12, which is the largest
number that is a factor of both. Dividing 12 by 12 yields 1;
dividing 60 by 12 yields 5. The reduced fraction is ![]() .
.
If you can’t immediately find the largest number
that is a factor of both, find any number that is a factor of both
and divide both the top and bottom by that. Your calculations will
take a little longer, but you’ll end up in the same place. In the
previous example, even if you don’t see that 12 is a factor of both
12 and 60, you can no doubt see that 6 is a factor of both. Dividing
top and bottom by 6 yields ![]() . Now
divide by 2. Doing so yields
. Now
divide by 2. Doing so yields ![]() . Once
again, you have arrived at ETS’s answer.
. Once
again, you have arrived at ETS’s answer.
A mixed number is a number such as ![]() . It
is the sum of an integer and a fraction. When you see mixed numbers
on the SAT, you should usually convert them to ordinary
fractions.
. It
is the sum of an integer and a fraction. When you see mixed numbers
on the SAT, you should usually convert them to ordinary
fractions.
Here’s a quick and easy way to convert mixed numbers.
For example, let’s convert ![]() to a
fraction. Multiply 2 (the integer part of the mixed number) by 4
(the bottom of the fraction). That gives you 8. Add that to the 3
(the top of the fraction) to get 11. Place 11 over 4 to get
to a
fraction. Multiply 2 (the integer part of the mixed number) by 4
(the bottom of the fraction). That gives you 8. Add that to the 3
(the top of the fraction) to get 11. Place 11 over 4 to get ![]() .
.
The mixed number ![]() is
exactly the same as the fraction
is
exactly the same as the fraction ![]() . We
converted the mixed number to a fraction because fractions are
easier to work with than mixed numbers.
. We
converted the mixed number to a fraction because fractions are
easier to work with than mixed numbers.
Try converting the following mixed numbers. Answers can be found here.
Joe Bloggs has trouble with fractions because
they don’t always behave the way he thinks they ought to. For
example, because 4 is obviously greater than 2, Joe Bloggs sometimes
forgets that ![]() is
less than
is
less than ![]() . He
becomes especially confused when the top is some number other than
1. For example,
. He
becomes especially confused when the top is some number other than
1. For example, ![]() is
less than
is
less than ![]() .
.
Joe also has a hard time understanding that when you multiply one fraction by another, you will get a fraction that is smaller than either of the first two. For example:
![]()
![]()
![]()
Throughout this section we’ve given you some hints about your calculator and fractions. While you should understand how to work with fractions the old-fashioned way, your calculator can be a tremendous help if you know how to use it properly. Make sure that you practice with your calculator so that working with fractions on it becomes second nature before the test.
Work these problems with the techniques you’ve read about in this chapter so far. Then check your answers by solving them with your calculator. If you have any problems, go back and review the information just outlined. Answers can be found here.
Fractions can be expressed as decimals. To find a fraction’s decimal equivalent, simply divide the top by the bottom. (You can do this easily with your calculator.) For example:
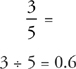
Manipulating decimals is easy with a calculator. Simply punch in the numbers—being especially careful to get the decimal point in the right place every single time—and read the result from the display. A calculator makes these operations easy. In fact, working with decimals is one area on the SAT where your calculator will prevent you from making careless errors. You won’t have to line up decimal points or remember what happens when you divide. The calculator will keep track of everything for you, as long as you punch in the correct numbers to begin with. Just be sure to practice carefully before you go to the test center.
Answers can be found here.
Some SAT problems will ask you to determine whether one decimal is larger or smaller than another. Many students have trouble doing this. It isn’t difficult, though, and you will do fine as long as you remember to line up the decimal points and fill in missing zeros.
Here’s an example:
Problem: Which is larger, 0.0099 or 0.01?
Solution: Simply place one decimal over the other with the decimal points lined up, like this:
![]()
To make the solution seem clearer, you can add two zeros to the right of 0.01. (You can always add zeros to the right of a decimal without changing its value.) Now you have this:
![]()
Which decimal is larger? Clearly, 0.0100 is,
just as 100 is larger than 99. (Remember that 0.0099 = ![]() ,
while 0.0100 =
,
while 0.0100 = ![]() . Now
the answer seems obvious, doesn’t it?)
. Now
the answer seems obvious, doesn’t it?)
Joe Bloggs has a terrible time on this problem. Because 99 is obviously larger than 1, he tends to think that 0.0099 must be larger than 0.01. But it isn’t. Don’t get sloppy on problems like this! ETS loves to trip up Joe Bloggs with decimals. In fact, any time you encounter a problem involving the comparison of decimals, you should stop and ask yourself whether you are about to make a Joe Bloggs mistake.
Many numbers are the product of the same factor multiplied over and over again. For example, 32 = 2 × 2 × 2 × 2 × 2. Another way to write this would be 32 = 25, or “thirty-two equals two to the fifth power.” The little number, or exponent , denotes the number of times that 2 is to be used as a factor. In the same way, 103 = 10 × 10 × 10, or 1,000, or “ten to the third power,” or “ten cubed.” In this example, the 10 is called the base and the 3 is called the exponent. (You won’t need to know these terms on the SAT, but you will need to know them to follow our explanations.)
When you multiply two numbers with the same base, you simply add the exponents. For example, 23 × 25 = 23+5 = 28.
When you divide two numbers with the same
base, you simply subtract the exponents. For example, ![]() =
23+5 = 28.
=
23+5 = 28.
When you raise a power to a power, you multiply the exponents. For example, (23)4 = 23 × 4 = 212
To remember the exponent rules, all you need to do is remember the acronym MADSPM. Here’s what it stands for:
Whenever you see an exponent problem, you should think MADSPM. The three MADSPM rules are the only rules that apply to exponents.
Here’s a typical ETS exponent problem:
![]()
14. For the equations ![]() =
a
10 and (a
y)3=a
x, if a > 1, what is the
value of x ?
=
a
10 and (a
y)3=a
x, if a > 1, what is the
value of x ?
| (A) | 5 |
| (B) | 10 |
| (C) | 15 |
| (D) | 20 |
| (E) | 25 |
Here’s How to Crack It
This problem looks pretty intimidating with all those variables. In fact, you might be about to cry “POOD” and go on to the next problem. That might not be a bad idea but before you skip the question, pull out those MADSPM rules.
For the first equation, you can use the Divide-Subtract rule: (a y )3 = a x-y = a10. In other words, the first equation tells you that x − y = 10.
For the second equation, you can use the Power-Multiply rule: (a y) = a 3 y =a x . So, that means that 3y = x.
Now, it’s time to substitute: x − y = 3y − y =10. So, 2y = 10 and y = 5. Be careful, though! Don’t choose answer A. That’s the value of y but the question wants to know the value of x. Since x = 3y, x = 3(5) = 15, which is answer C.
Don’t forget that you could also do this question by plugging in the answer choices. Of course, you still need to know the MADSPM rules to do the question that way.
![]()
You can compute simple exponents on your calculator. Make sure you have a scientific calculator with a y x key. To find 210, for example, simply use your y x key, punching 2 in for the y value and 10 in for the x value. This may be especially useful if you are asked to compare exponents.
Raising a number to a power can have quite peculiar and unexpected results, depending on what sort of number you start out with. Here are some examples.
For example, ![]() .
.
You should also have a feel for relative sizes of exponential numbers without calculating them. For example, 210 is much larger than 102. (210 = 1,024; 102 = 100.) To take another example, 25 is twice as large as 24, even though 5 seems only a bit larger than 4.
The radical sign (![]() )
indicates the square root of a number. For example,
)
indicates the square root of a number. For example, ![]() =
5. Note that square roots cannot be negative. If ETS wants you to
think about a negative solution they’ll say x
2= 25 because then x = 5 or x
= –5.
=
5. Note that square roots cannot be negative. If ETS wants you to
think about a negative solution they’ll say x
2= 25 because then x = 5 or x
= –5.
Here are the only rules regarding square roots that you need to know for the SAT:
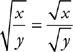 .
For example,
.
For example,
Note that rule 1 works in reverse: ![]() . This
is really a kind of factoring. You are using rule 1 to factor a
large, clumsy radical into numbers that are easier to work with. And
remember that radicals are just fractional exponents, so the same
rules of distribution apply.
. This
is really a kind of factoring. You are using rule 1 to factor a
large, clumsy radical into numbers that are easier to work with. And
remember that radicals are just fractional exponents, so the same
rules of distribution apply.
Don’t make careless mistakes. Remember that
the square root of a number between 0 and 1 is larger than
the original number. For example, ![]() , and
, and
![]() .
.
So far we’ve dealt with only positive integers for exponents, but they can be negative integers as well as fractions. The same concepts and rules apply, but the numbers just look a little weirder. Keep these concepts in mind:
![]()
![]()
![]()
18. If x > 0, which of the
following is equivalent to ![]() ?
?
![]()
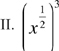
![]()
| (A) | None |
| (B) | I and II only |
| (C) | I and III only |
| (D) | II and III only |
| (E) | I, II and III |
Here’s How to Crack It
This problem really tests your knowledge of
exponents. First, convert ![]() into
an exponent since all the roman numerals contain expressions with
exponents. (Plus, exponents are easier to work with because they
have those nice MADSPM rules.) So, using the definition of a
fractional exponent,
into
an exponent since all the roman numerals contain expressions with
exponents. (Plus, exponents are easier to work with because they
have those nice MADSPM rules.) So, using the definition of a
fractional exponent,![]() . You
want the items in the roman numerals to equal
. You
want the items in the roman numerals to equal ![]() .
.
Now, it’s time to start working with the roman
numerals. For roman numeral I, ETS is trying to be tricky. (There’s
a surprise.) There’s no exponent rule for adding exponent
expressions with like bases. So,![]() . (If
you were uncertain, you could try a number for x. If
x = 4, then
. (If
you were uncertain, you could try a number for x. If
x = 4, then ![]() but
but
![]() .)
Cross off any answer with roman numeral I. So, B, C and E are all
gone.
.)
Cross off any answer with roman numeral I. So, B, C and E are all
gone.
Now, all you really need to do is try either II
or III. If either works, the answer is D. For roman numeral II, use
the power-multiply rule: 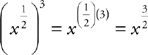 . So,
since roman numeral II works, D is the correct answer.
. So,
since roman numeral II works, D is the correct answer.
If you simply must know what’s going on with
roman numeral III, use the multiply-add rule: 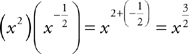 . But,
remember that you had already chosen an answer. Using good POE on a
roman numeral question often means that you don’t need to check all
the roman numerals.
. But,
remember that you had already chosen an answer. Using good POE on a
roman numeral question often means that you don’t need to check all
the roman numerals.
![]()
![]()
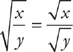
![]()
![]()