Ten of the fifty-four math questions found on the SAT will require you to produce your own answer. Although the format of these questions is different from that of the multiple-choice questions, the mathematical concepts tested are no different. In this chapter we will show you how to apply what you have learned in the previous chapters to these new questions.
One of the Math sections on your SAT will contain a group of ten problems without multiple-choice answers. ETS calls these problems “Student-Produced Responses.” We call them Grid-Ins, because you have to mark your answers on a grid printed on your answer sheet. The grid looks like this:
Despite their format, Grid-Ins are just like other math questions on the SAT, and many of the techniques that you’ve learned so far still apply. You can still use Plugging In and other great techniques, such as the Ratio Box and the Average Pie. You can still use the order of difficulty and your knowledge of Joe Bloggs to avoid making obvious mistakes on hard questions. Your calculator will still help you out on many problems as well. So Grid-Ins are nothing to be scared of. In fact, many Grid-In questions are simply regular SAT multiple-choice math problems with the answer choices lopped off. The only difference is that you have to arrive at your answer from scratch, rather than choose from among five possibilities.
You will need to be extra careful when answering Grid-In questions, however, because the grid format increases the likelihood of careless errors. It is vitally important that you understand how the Grid-In format works before you take the test. In particular, you’ll need to memorize ETS’s rules about which kinds of answers count and which don’t. The instructions may look complicated, but we’ve boiled them down to a few rules for you to memorize and practice.
Take a look at the grid again. Because of the way it’s arranged, ETS can use only certain types of problems for Grid-Ins. For example, you’ll never see variables (letters) in your answer (although there can be variables in the question), because the grid can only accommodate numbers. This is good for you because no matter how good you are at algebra, you’re probably better at arithmetic.
Also, this means that your calculator will be useful on several questions. As always, be careful to set up the problem on paper before you carefully punch the numbers into your calculator. Because you have to write in the answer on the grid yourself, you have to be more careful than ever to avoid careless mistakes.
Grid-Ins are scored somewhat differently than multiple-choice questions on the SAT. On multiple-choice questions, you lose a fraction of a raw score point for every incorrect answer. However, nothing is deducted for an incorrect answer on a Grid-In. An incorrect answer on one of these questions is no worse for your score than a question left blank. And, by the same token, a blank is just as costly as an error. Therefore, you should be very aggressive in answering these questions. Don’t leave a question blank just because you’re worried that the answer you’ve found may not be correct. ETS’s scoring computers treat incorrect answers and blanks exactly the same. If you have arrived at an answer, you have a shot at earning points, and if you have a shot at earning points, you should take it.
We’re not saying guess blindly. But if you work a problem and are unsure of your answer, enter it anyway. There is no penalty for getting it wrong.
Here are the instructions for the Grid-In sections as they will appear on your SAT:
Click here to view a larger image.
Of all the instructions on the SAT, these are the most important to understand thoroughly before you take the test. Pity the unprepared student who takes the SAT cold and spends ten minutes of potential point-scoring time reading and puzzling over ETS’s confusing instructions. We’ve translated these unnecessarily complicated instructions into a few important rules. Make sure you know them all well.
Always write your answer in the boxes at the top of the grid before you darken the ovals below. Your written answers won’t affect the scoring of your test; if you write the correct answer in the boxes and grid in the wrong ovals, you won’t get credit for your answer (and you won’t be able to appeal to ETS). However, writing in the answers first makes you less likely to make an error when you grid in, and it also makes it easier to check your work.
As we just pointed out, you receive no credit for writing in the answer at the top of the grid. ETS’s computer cares only whether the ovals are filled in correctly. For every number you write into the grid, make sure that you fill in the corresponding oval.
Although you’ll receive credit no matter where you put your answer on the grid, you should always begin writing your answer in the far left column of the grid. This ensures that you will have enough space for longer answers when necessary. You’ll also cut down on careless errors if you always grid in your answers the same way.
You can grid in an answer in either fraction or decimal form. For example, if your answer to a question is 
, you can either grid in
or .5. It doesn’t matter to ETS because equals .5; the computer will credit either form of the answer. That means you actually have a choice. If you like fractions, grid in your answers in fraction form. If you like decimals, you can grid in the decimal. If you have a fraction that doesn’t fit in the grid, you can simply convert it to a decimal on your
calculator and grid in the decimal.
Here’s the bottom line: When gridding in fractions or decimals, use whichever form is easier and least likely to cause careless mistakes.
When you have a decimal answer of a value less than 1, such as .45 or .678, many teachers ask you to write a zero before the decimal point (for example, 0.45 or 0.678). On Grid-In questions, however, ETS doesn’t want you to worry about the zero. In fact, there is no 0 in the first column of the grid. If your answer is a decimal less than 1, just write the decimal point in the first column of the grid and then continue from there.
You should also notice that if you put the decimal point in the first column of the grid, you have only three places left to write in numbers. But what if your decimal is longer than three places, such as .87689? In these cases, ETS will give you credit if you round off the decimal so that it fits in the grid. But you’ll also get credit, however, if you just enter as much of the decimal as will fit.
For example, if you had to grid in .87689, you could just write .876 (which is all that will fit) and then stop. You need to grid in only whatever is necessary to receive credit for your answer. Don’t bother with extra unnecessary steps. You don’t have to round off decimals, so don’t bother.
If you have a long or repeating decimal, however, be sure to fill up all the spaces in the grid. If your decimal is .666666, you must grid in .666. Just gridding in .6 or .66 is not good enough.
If you decide to grid in a fraction, ETS doesn’t care if you reduce the fraction or not. For example, if your answer to a problem is 
, ETS will give you credit if you grid in or reduce it to 
. So if you have to grid in a fraction, and the fraction fits in the grid, don’t bother reducing it. Why give yourself more work (and another chance to make a careless error)?
The only time you might have to reduce a fraction is if it doesn’t fit in the grid. If your answer to a question is 
, it won’t fit in the grid. You have two options: Either reduce the fraction to 
and grid that in, or use your calculator to convert
the fraction to .6. Choose whichever process makes you the most comfortable.
ETS’s scoring machine does not recognize mixed numbers. If you try to grid in 
by writing “2 1/2,” the computer will read this number as 
. You have to convert mixed numbers to fractions or decimals before you grid them in. To grid in 
, either convert it to 
or its decimal equivalent, which is 2.5. If you have to convert a mixed number to grid it in, be very careful not to change its value accidentally.
The vast majority of Grid-In answers will not be difficult to enter in the grid. ETS won’t try to trick you by purposely writing questions that are confusing to grid in. Just pay attention to these guidelines and watch out for careless errors.
To get a feel for this format, let’s work through two examples. As you will see, Grid-In problems are just regular SAT math problems.
10. If a + 2 = 6 and b + 3 = 21, what is the value of 
?
Here’s How to Crack It
You need to solve the first equation for a and the second equation for b. Start with the first equation, and solve for a. By subtracting 2 from both sides of the equation, you should see that a = 4.
Now move to the second equation, and solve for b. By subtracting 3 from both sides of the second equation, you should see that b = 18.
The question asked you to find the value of . That’s easy. The value of b is 18, and the value of a is 4. Therefore, the value of is 
.
That’s an ugly-looking fraction. How in the world do you grid it in? Ask yourself: “Does fit?” Yes! Grid in .
Your math teacher wouldn’t like it, but ETS’s computer will. You shouldn’t waste time reducing to a prettier fraction or converting it to a decimal. Spend that time on another problem instead. The fewer steps you take, the less likely you will be to make a careless mistake.
Here’s another example. This one is quite a bit harder.
15. Forty percent of the members of the sixth-grade class wore white socks. Twenty percent wore black socks. If twenty-five percent of the remaining students wore gray socks, what percent of the sixth-grade class wore socks that were not white, black, or gray? (Disregard the when gridding your answer.)
Here’s How to Crack It
The problem doesn’t tell you how many students are in the class, so you can plug in any number you like. This is a percentage problem, so the easiest number to plug in is 100. Forty percent of 100 is 40; that means 40 students wore white socks. Twenty percent of 100 is 20. That means that 20 students wore black socks.
Your next piece of information says that 25 percent of the remaining students wore gray socks. How many students remain? Forty, because 60 students wore either white or black socks, and 100 – 60 = 40. Therefore, 25 percent of these 40—10 students—wore gray socks.
How many students are left? 30. Therefore, the percentage of students not wearing white, black, or gray socks is 30 out of 100, or 30 percent. Grid it in, and remember to forget about the percent sign.
Like all other questions on the Math SAT, Grid-In problems are arranged in order of increasing difficulty. In each group of ten, the first third is easy, the second third is medium, and the final third is difficult. As always, the order of difficulty will be your guide to how much faith you can place in your hunches.
Remember to focus on the questions you know how to answer first. Don’t spend time on questions that you have no idea how to work, but if you’re able to plug in or take an educated guess, go ahead and grid in that answer. Again, there’s no penalty for getting it wrong.
Keep in mind, of course, that many of the math techniques that you’ve learned are still very effective on Grid-In questions. Plugging In worked very well on question number 15 on the previous page.
Here’s another difficult Grid-In question that you can answer effectively by using a technique you’ve learned before:
18. Grow-Up potting soil is made from only peat moss and compost in a ratio of 3 pounds of peat moss to 5 pounds of compost. If a bag of Grow-Up potting soil contains 12 pounds of potting soil, how many pounds of peat moss does it contain?
To solve this problem, set up a Ratio Box (the Ratio Box is explained in detail in Chapter 13).
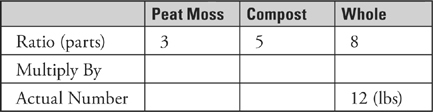
What do you multiply by 8 to get 12? If you don’t know, divide 12 by 8 on your calculator. The answer is 1.5. Write 1.5 in each of the boxes on the multiply by row of your Ratio Box.
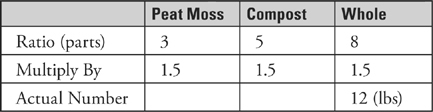
The problem asks you how many pounds of peat moss are in a bag. To find out, multiply the numbers in the Peat Moss column. That is, multiply 3 × 1.5, and you get 4.5. ETS’s answer is 4.5.
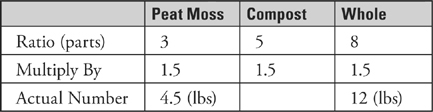
Grid it in like this:
On Grid-In questions, you obviously can’t use the Joe Bloggs principle to eliminate tempting but incorrect answer choices, because there aren’t any choices from which to choose. But you can—and must—use your knowledge of Joe Bloggs to double-check your work and keep yourself from making careless mistakes or falling into traps.
The basic idea still holds true: Easy questions have easy answers, and hard questions have hard answers. On hard questions, you must be extremely suspicious of answers that come to you easily or through simple calculations.
Unfortunately, your knowledge of Joe Bloggs alone will never lead you all the way to ETS’s answers, the way it sometimes does on multiple-choice questions. In order to earn points on Grid-In questions, you’re going to have to find the real answers, and you’re going to have to be extremely careful when you enter your answers on your answer sheet. But Joe Bloggs may help you find the correct path to ETS’s answer. On a hard problem, you may be torn between two different approaches, one easy and one hard. Which should you pursue? The harder one. Joe will take the easy path and, as always on hard questions, it will lead him to the wrong answer.
Some Grid-In problems will have many possible correct answers. It won’t matter which correct answer you choose, as long as the one you choose really is correct.
12. What is one possible value of x such that 
< x < 
?
Here’s How to Crack It
Joe Bloggs has trouble imagining how anything could squeeze between and , but you know there are lots and lots of numbers in there. Any one of them will satisfy ETS.
The numbers in this problem are both fractions, but your answer doesn’t have to be. The easiest approach is to forget about math-class solutions and head straight for your calculator (or your mental calculator). Convert to a decimal by dividing 1 by 4, which gives you .25. Now convert to a decimal by dividing 1 by 3, which gives you .333. All you need to answer the question is any number that falls between those two decimals. How about .26? Or .3? Or .331? Your answer merely has to be bigger than .25 and smaller than .333. Pick one, grid it in, and move on.
