
Click here to download a PDF of Practice Test 1.

DO NOT OPEN THIS BOOKLET UNTIL YOU ARE TOLD TO DO SO.

Instructions
Section I of this exam contains 40 multiple-choice questions. Fill in only the ovals for numbers 1 through 40 on your answer sheet.
Indicate all of your answers to the multiple-choice questions on the answer sheet. No credit will be given for anything written in this exam booklet, but you may use the booklet for notes or scratch work. After you have decided which of the suggested answers is best, completely fill in the corresponding oval on the answer sheet. Give only one answer to each question. If you change an answer, be sure that the previous mark is erased completely. Here is a sample question and answer.
Sample Question
Omaha is a
(A) state
(B) city
(C) country
(D) continent
(E) village
Sample Answer

Use your time effectively, working as quickly as you can without losing accuracy. Do not spend too much time on any one question. Go on to other questions and come back to the ones you have not answered if you have time. It is not expected that everyone will know the answers to all of the multiple-choice questions.
About Guessing
Many candidates wonder whether or not to guess the answers to questions about which they are not certain. Multiple–choice scores are based on the number of questions answered correctly. Points are not deducted for incorrect answers, and no points are awarded for unanswered questions. Because points are not deducted for incorrect answers, you are encouraged to answer all multiple-choice questions. On any questions you do not know the answer to, you should eliminate as many choices as you can, and then select the best answer among the remaining choices.
Once you have checked your answers, remember to return to this page and respond to the Reflect questions.
STATISTICS
SECTION I
Time—1 hour and 30 minutes
Number of questions—40
Percent of total grade—50
Directions: Solve each of the following problems, using the available space for scratchwork. Decide which is the best of the choices given and fill in the corresponding oval on the answer sheet. No credit will be given for anything written in the test book. Do not spend too much time on any one problem.
1. An outlier is an observation that
(A) is seen more frequently than the other observations in the data set
(B) is seen less frequently than the other observations in the data set
(C) is always smaller than the other observations in the data set
(D) is always larger than the other observations in the data set
(E) is significantly different from the other observations in the data set
2. During flu season, a city medical center needs to keep a large supply of flu shots. A nurse’s aid compiles data on the number of flu shots given per day in the past few years during flu season. A cumulative probability chart of the collected data is as follows:
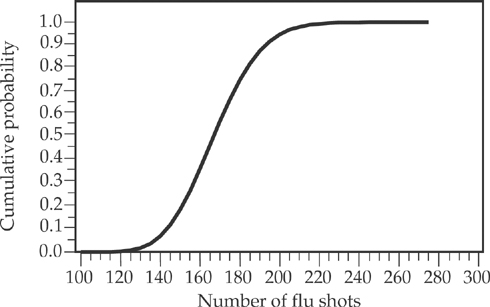
How many flu shots should the center store every day to meet the demand on 95 percent of the days?
(A) At most 190
(B) At most 140
(C) Exactly 170
(D) At least 150
(E) At least 200
3. A large company has offices in two locations, one in New Jersey and one in Utah. The mean salary of office assistants in the New Jersey office is $28,500. The mean salary of office assistants in the Utah office is $22,500. The New Jersey office has 128 office assistants and the Utah office has 32 office assistants. What is the mean salary paid to the office assistants in this company?
(A) $22,500
(B) $23,700
(C) $25,500
(D) $27,300
(E) $28,500
4. In the northern United States, schools are sometimes closed during winter due to severe snowstorms. At the end of the school year, schools have to make up for the days missed. The following graph shows the frequency distribution of the number of days missed due to snowstorms per year using data collected from the past 75 years.
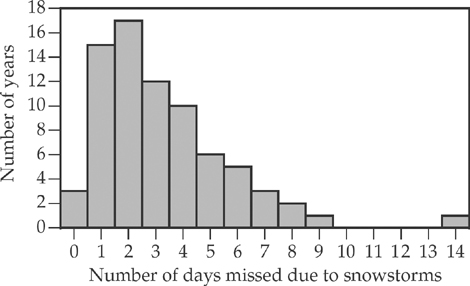
Which of the following should be used to describe the center of this distribution?
(A) Mean, because it is an unbiased estimator
(B) Median, because the distribution is skewed
(C) IQR, because it excludes outliers and includes only the middle 50 percent of data
(D) First quartile, because the distribution is left skewed
(E) Standard deviation, because it is unaffected by the outliers
5. The probability that there will be an accident on Highway 48 each day depends on the weather. If the weather is dry that day, there is a 0.2% chance of an accident on Highway 48; if the weather is wet that day, there is a 1.0% chance of an accident. Today, the weather station announced that there is a 20% chance of the weather being wet. What is the probability that there will be an accident on Highway 48 today?
(A) 0.0004
(B) 0.0016
(C) 0.0020
(D) 0.0036
(E) 0.0060
6. An employment placement agency specializes in placing workers in jobs suited for them. From past experience, the agency knows that 20% of all the workers it places will no longer be at the position in which they were placed after one year; however, only 5% of those remaining after the first year leave during the next year. At the start of a year an employer hires 100 workers using this agency, then at the start of the next year the employer hires 100 more. How many of these 200 workers are expected to be on the job at the end of the second year?
(A) 140
(B) 144
(C) 152
(D) 156
(E) 171
7. The average number of calories in Yum-Yum Good candy bars is 210, with a standard deviation of 10. If the number of calories per candy bar is normally distributed, what percent of candy bars contain more than 225 calories?
(A) 66.8%
(B) 47.7%
(C) 43.3%
(D) 6.68%
(E) 3.34%
8. A publisher used standard boxes for shipping books. The mean weight of books packed per box is 25 pounds, with a standard deviation of two pounds. The mean weight of the boxes is one pound, with a standard deviation of 0.15 pounds. The mean weight of the packing material used per box is two pounds, with a standard deviation of 0.25 pounds. What is the standard deviation of the weights of the packed boxes?
(A) 28.000 pounds
(B) 5.290 pounds
(C) 4.085 pounds
(D) 2.400 pounds
(E) 2.021 pounds
9. The principal of a school is interested in estimating the average income per family of her students. She selects a random sample of students and collects information about their family income. A 95 percent confidence interval computed from this data for the mean income per family is ($35,095, $45,005). Which of the following provides the best interpretation of this confidence interval?
(A) 95 percent of the students in her school are from families whose income is between $35,095 and $45,005.
(B) There is a 95% probability that the families of all the students in this school have an income of between $35,095 and $45,005.
(C) If we were to take another sample of the same size and compute a 95 percent confidence interval, we would have a 95% chance of getting the interval ($35,095, $45,005).
(D) There is a 95% probability that the mean of another sample with the same size will fall between $35,095 and $45,005.
(E) There is a 95% probability that the mean income per family in the school is between $35,095 and $45,005.
10. The Department of Health plans to test the lead level in a specific park. Because a high lead level is harmful to children, the park will be closed if the lead level exceeds the allowed limit. The department randomly selects several locations in the park, gets soil samples from those locations, and tests the samples for their lead levels. Which of the following decisions would result from the type I error?
(A) Closing the park when the lead levels are within the allowed limit
(B) Keeping the park open when the lead levels are in excess of the allowed limit
(C) Closing the park when the lead levels are in excess of the allowed limit
(D) Keeping the park open when the lead levels are within the allowed limit
(E) Closing the park because of the increased noise level in the neighborhood
11. Extra study sessions were offered to students after the midterm to help improve their understanding of statistics. Student scores on the midterm and the final exam were recorded. The following scatterplot shows final test scores against the midterm test scores.
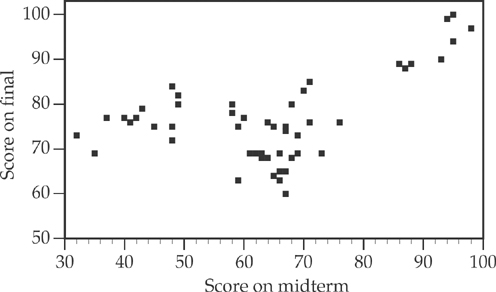
Which of the following statements correctly interprets the scatterplot?
(A) All students have shown significant improvement in the final exam scores as a result of the extra study sessions.
(B) The extra study sessions were of no help. Each student’s final exam score was about the same as his or her score on the midterm.
(C) The extra study sessions further confused students. All student scores decreased from midterm to final exam.
(D) Students who scored below 55 on the midterm showed considerable improvement on the final exam; those who scored between 55 and 80 on the midterm showed minimal improvement on the final exam; and those who scored above 80 on the midterm showed almost no improvement on the final exam.
(E) Students who scored below 55 on the midterm showed minimal improvement on the final exam; those who scored between 55 and 80 on the midterm showed moderate improvement on the final exam; and those who scored above 80 on the midterm showed considerable improvement on the final exam.
12. A resident of Auto Town was interested in finding the cheapest gas prices at nearby gas stations. On randomly selected days over a period of one month, he recorded the gas prices (in dollars) at four gas stations near his house. The boxplots of gas prices are as follows:
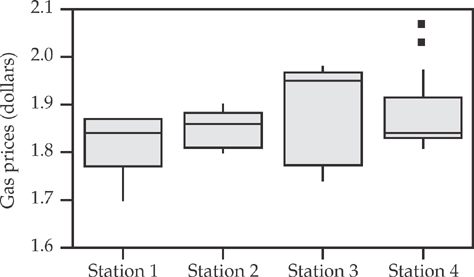
Based on this display, which of the stations had the closest mean and median during the month?
(A) Station 1
(B) Station 2
(C) Station 3
(D) Station 4
(E) We cannot tell without knowing the standard deviation of the gas prices from each station.
13. A botanist is interested in testing H0: µ = 3.5 cm versus Ha: µ > 3.5, where µ = the mean petal length of one variety of flowers. A random sample of 50 petals gives significant results at a 5 percent level of significance. Which of the following statements about the confidence interval to estimate the mean petal length is true?
(A) The specified mean length of 3.5 cm is within a 90 percent confidence interval.
(B) The specified mean length of 3.5 cm is not within a 90 percent confidence interval.
(C) The specified mean length of 3.5 cm is below the lower limit of a 90 percent confidence interval.
(D) The specified mean length of 3.5 cm is below the lower limit of a 95 percent confidence interval.
(E) Not enough information is available to answer the question.
14. A filling machine puts an average of four ounces of coffee in jars, with a standard deviation of 0.25 ounces. Forty jars filled by this machine are selected at random. What is the probability that the mean amount per jar filled in the sampled jars is less than 3.9 ounces?
(A) 0.0057
(B) 0.0225
(C) 0.0250
(D) 0.0500
(E) 0.3446
15. The number of customers served per day by a large department store is normally distributed, with a mean of 3,250 customers and a standard deviation of 320. Find the range of customers served on the middle 50 percent of days.
(A) (3,034, 3,466)
(B) (2,930, 3,570)
(C) (2,610, 3,890)
(D) (2,450, 4,050)
(E) (2,290, 4,210)
16. Assume that the masses of chicken eggs are normally distributed with a mean of 45 g and a standard deviation of 4 g. What mass of egg would be the 25th percentile of the masses of all the eggs?
(A) 42.2 g
(B) 42.3 g
(C) 42.4 g
(D) 42.5 g
(E) 42.6 g
17. The observed times (in minutes) it takes a runner to complete a marathon are normally distributed. The z-score for his running time this week is –2. Which one of the following statements is a correct interpretation of his z-score?
(A) This week his time was two minutes lower than his time last week.
(B) This week his time was two minutes lower than his best time ever.
(C) This week his time was two minutes lower than his average time.
(D) This week his time was two standard deviations lower than his average time.
(E) This week his time was two standard deviations lower than his time last week.
18. For which of these is a binomial probability model most reasonable?
(A) The number of times, out of 10 attempts, that a particular child can throw a ball into a basket from six feet away
(B) The colors of the cars in the parking lot of a particular grocery store on a randomly selected Sunday
(C) The number of times that a randomly selected resident of California has visited a museum in the last 12 months
(D) The number of cards drawn from a well-shuffled deck until all four aces are found
(E) The number of people surveyed until someone who owns a parrot is found
19. A dentist has noticed that about two children in every seven whom he sees professionally develop cavities before they turn 10 years old. Last week he examined the teeth of five unrelated children younger than 10. Let X be the number of children who develop cavities before turning 10. Which of the following gives the probability that at least one will develop a cavity before turning 10?
(A) P(X = 2, 3, 4, 5, 6, 7)
(B) P(X = 2 out of 7)
(C) P(X = 1)
(D) 1 – P(X = 0)
(E) P(X = 0, 1)
20. The probability that Ted enrolls in an English class is  . If he does enroll in an English class, the probability that he enrolls in a mathematics class is
. If he does enroll in an English class, the probability that he enrolls in a mathematics class is  . If he does not enroll in an English class, the probability that he enrolls in a mathematics class is
. If he does not enroll in an English class, the probability that he enrolls in a mathematics class is  . If we learn that Ted enrolled in a mathematics class, what is the probability that he enrolled in an English class?
. If we learn that Ted enrolled in a mathematics class, what is the probability that he enrolled in an English class?
(A) 0.067
(B) 0.143
(C) 0.250
(D) 0.333
(E) 0.500
21. Two dice are rolled simultaneously. If both dice show 6, then the player wins $20; otherwise the player loses the game. It costs $2.00 to play the game. What is the expected gain or loss per game?
(A) The player will gain about $0.55.
(B) The player will gain about $1.44.
(C) The player will lose about $0.55.
(D) The player will lose about $1.44.
(E) The player will lose about $2.00.
22. According to the central limit theorem, the sample mean X is approximately normally distributed
(A) for a large sample, regardless of the distribution of random variable X
(B) for a large sample, provided the random variable X is normally distributed
(C) regardless of the sample size
(D) for a small sample, regardless of the distribution of random variable X
(E) for a small sample, provided the random variable X is normally distributed
23. A department store at a large mall claims that over 60 percent of the mall’s visitors shop at that store. Let p = the proportion of the mall’s visitors who shop at the store. Which of the following pairs of hypotheses should be used to support this claim?
(A) H0: p ≤ 0.60 and Ha: p > 0.60
(B) H0: p = 0.60 and Ha: p 0.60
(C) H0: p = 0.60 and Ha: p < 0.60
(D) H0: p > 0.60 and Ha: p 0.60
(E) H0: p < 0.60 and Ha: p 0.60
24. A random sample of 16 light bulbs of one brand was selected to estimate the mean lifetime of that brand of bulbs. The sample mean was 1,025 hours, with a standard deviation of 130 hours. Assuming that the lifetimes are approximately normally distributed, which of the following will give a 95 percent confidence interval to estimate the mean lifetime?
(A) 1,025 ± 1.96 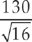
(B) 1,025 ± 1.96 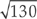
(C) 1,025 ± 2.12 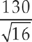
(D) 1,025 ± 2.13 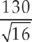
(E) 1,025 ± 2.13 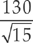
25. A school committee member is lobbying for an increase in the gasoline tax to support the county school system. The local newspaper conducted a survey of county residents to assess their support for such an increase. What is the population of interest here?
(A) All school-aged children
(B) All county residents
(C) All county residents with school-aged children
(D) All county residents with children in the county school system
(E) All county school system teachers
26. A manufacturer of ready-bake cake mixes is interested in designing an experiment to test the effects of four different temperature levels (300, 325, 350, and 375F), two different types of pans (glass and metal), and three different types of ovens (gas, electric, and microwave) on the texture of its cakes, in all combinations. Which of the following below is the best description of the design of the necessary experiment?
(A) A completely randomized design with nine treatment groups
(B) A completely randomized design with 24 treatment groups
(C) A randomized block design, blocked on temperature, with six treatment groups
(D) A randomized block design, blocked on type of pan, with 12 treatment groups
(E) A randomized block design, blocked on type of oven, with eight treatment groups
27. Which one of the following distributions could have a mean of approximately 12 and a standard deviation of approximately two?
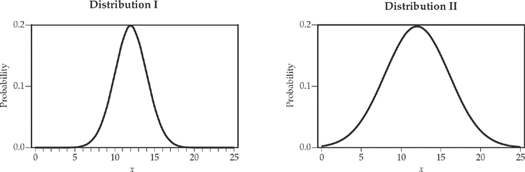
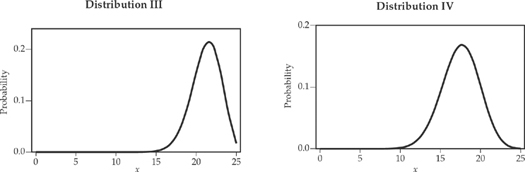
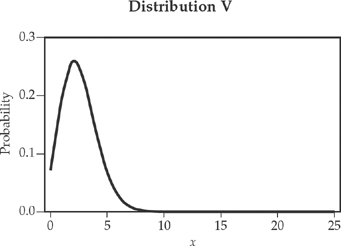
(A) Distribution I
(B) Distribution II
(C) Distribution III
(D) Distribution IV
(E) Distribution V
28. The relation between the selling price of a car (in $1,000) and its age (in years) is estimated from a random sample of cars of a specific model. The relation is given by the following formula:
Selling price = 15.9 – 0.983 (age)
Which of the following can we conclude from this equation?
(A) For every year the car gets older, the selling price goes down by approximately 9.83 percent.
(B) A new car costs on the average $9,830.
(C) For every year the car gets older, the selling price drops by approximately $1,590.
(D) A new car costs $16,883.
(E) For every year the car gets older, the selling price drops by approximately $983.
29. Which of the following is true about any discrete probability distribution of a random variable X?
(A) The expected value of X = np.
(B) The sum of all possible values of X is equal to one.
(C) The probabilities of all possible values of X must add up to one.
(D) The probability distribution is bell-shaped and symmetric.
(E) Approximately 95 percent of the values of X fall within two standard deviations of the mean.
30. X and Y are independent random variables; the probability distributions for each are given in the table above. Let Z = X + Y. What is P(Z ≤ 2)?
(A) 0.07
(B) 0.15
(C) 0.24
(D) 0.40
(E) 0.80
31. After a frost warning was issued, the owner of a large orange grove asked his workers to spray all his trees with water. The water was supposed to freeze and form a protective covering of ice around the orange blossom. Nevertheless, the owner suspected that some trees suffered considerable damage due to the frost. To estimate the proportion of trees that suffered more than 50 percent damage due to the frost, he took a random sample of 100 trees from his grove. What is the response variable in this experiment?
(A) The proportion of trees that suffered more than 50 percent damage due to frost.
(B) The number of trees affected by the frost.
(C) The number of trees sampled from the grove.
(D) For each sampled tree, whether it was sprayed with water or not sprayed with water.
(E) For each sampled tree, whether it suffered more than 50 percent damage or at most 50 percent damage.
32. For which of the following purposes would it be most unreasonable to use a census?
(A) To determine the proportion of students with a learning disability in a small rural area high school
(B) To determine the proportion of red snappers with a high mercury level in the Gulf of Mexico
(C) To determine the difference between the proportion of engineering professors and the proportion of business professors in favor of the new teaching initiative at a large university
(D) To determine the mean wage earned by construction workers in a small town
(E) To determine the mean selling price of houses in your neighborhood
33. A student organization at a university is interested in estimating the proportion of students in favor of showing movies biweekly instead of monthly. How many students should be sampled to get a 90 percent confidence interval with a width of at most 0.08?
(A) 27
(B) 64
(C) 106
(D) 256
(E) 423
34. A small kiosk at the Atlanta airport carries souvenirs in the price range of $3.99 to $29.99, with a mean price of $14.75. The airport authorities decide to increase the rent charged for a kiosk by 5 percent. To make up for the increased rent, the kiosk owner decides to increase the prices of all items by 50 cents. As a result, which of the following will happen?
(A) The mean price and the range of prices will increase by 50 cents.
(B) The mean price will remain the same, but the range of prices will increase by 50 cents.
(C) The mean price and the standard deviation of prices will increase by 50 cents.
(D) The mean price will increase by 50 cents, but the standard deviation of prices will remain the same.
(E) The mean price and the standard deviation will remain the same.
35. Two hundred students were classified by sex and hostility level (low, medium, high), as measured by an HLT-test. The results were the following:
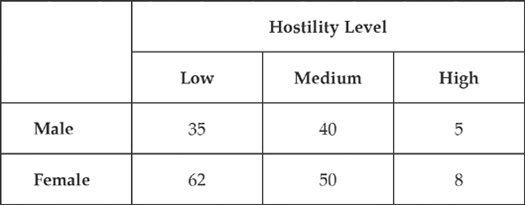
If the hostility level among students were independent of their sex, then how many female students would we expect to show the medium HLT score?
(A) 25
(B) 45
(C) 54
(D) 60
(E) 75
36. After receiving several complaints from his customers about the store being closed on Sundays, a storekeeper decided to conduct a survey. He randomly selected 100 female customers and 120 male customers, and asked them, “Are you interested in shopping at this store on Sundays?” He counted the number of customers answering “yes” and constructed a 95 percent confidence interval for the difference by subtracting the proportions of female from the proportion of male customers in favor of shopping on Sundays. The resulting interval was (–0.23, –0.18). Which of the following is a correct interpretation of the interval?
(A) We are 95 percent confident that the proportion of women interested in shopping on Sundays exceeds the proportion of men interested in shopping on Sundays.
(B) We are 95 percent confident that the proportion of men interested in shopping on Sundays exceeds the proportion of women interested in shopping on Sundays.
(C) We are 95 percent confident that the proportion of women interested in shopping on Sundays is equal to the proportion of men interested in shopping on Sundays.
(D) Because the interval contains negative values, it is invalid and should not be interpreted.
(E) Because the interval does not contain zero, the interval is invalid, and should not be interpreted.
37. A company is interested in comparing the mean sales revenue per salesperson at two different locations. The manager takes a random sample of 10 salespeople from each location independently and records the sales revenue generated by each person during the last four weeks. He decides to use a t-test to compare the mean sales revenue at the two locations. Which of the following assumptions is necessary for the validity of the t-test?
(A) The population standard deviations at both locations are equal.
(B) The population standard deviations at both locations are not equal.
(C) The population standard deviations at both locations are known.
(D) The population of the sales records at each location is normally distributed.
(E) The population of the difference in sales records computed by pairing one salesperson from each location is normally distributed.
38. A skeptic decides to conduct an experiment in ESP in which a blindfolded subject calls out the color of a card dealt from a regular deck of cards (half the cards are red; the other half, black). One hundred cards are dealt from a well-shuffled pack, with each card being replaced after a deal. Using a 5 percent level of significance, what is the lowest number of cards that the subject needs to call out correctly in order to show that he is doing better than he would if he were simply guessing?
(A) 51
(B) 59
(C) 75
(D) 95
(E) 98
39. A manufacturer of motor oil is interested in testing the effects of a newly developed additive on the lifespan of an engine. Twenty-five different engine types are selected at random and each one is tested using oil with the additive and oil without the additive. What type of analysis will yield the most useful information?
(A) Matched pairs comparison of population proportions
(B) Matched pairs comparison of population means
(C) Independent samples comparison of population proportions
(D) Independent samples comparison of population means
(E) Chi-square test of homogeneity
40. A chi-squared test of independence is to be performed on a 3 × 4 contingency table. How many degrees of freedom does this test have?
(A) 6
(B) 8
(C) 10
(D) 11
(E) 12
END OF SECTION I
STATISTICS
SECTION II
Time—1 hour and 30 minutes
Number of questions—6
Percent of total grade—50
Part A
Questions 1–5
Spend about 60 minutes on this part of the exam.
Percent of Section II grade—75
Show all your work. Indicate clearly the methods you use, because you will be graded on the correctness of your method as well as on the accuracy of your results and explanation.
1. A chemical engineering company has developed two different catalysts to accelerate a chemical reaction necessary for one of its products. To test the speed of the reaction of the two catalysts, it uses catalyst A 12 times in the reaction, then catalyst B 12 times in the reaction. Each of the 12 trials for both catalysts is conducted under identical controlled conditions, and the time it takes (in seconds) for the reaction to complete is measured. The results are shown in the table below:
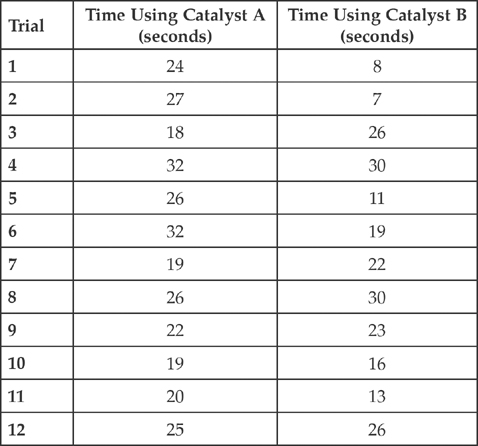
(a) Display the data using two box-and-whisker plots in the space below.
(b) If the chemical company is most interested in making the reaction time as short as possible, which catalyst should it use? Please explain.
(c) If the chemical company is most interested in making the reaction time as consistent as possible, which catalyst should it use? Please explain.
2. A vegetable oil blend packaged by a food manufacturer consists of canola oil and corn oil. The amount of canola oil in each bottle of the blend can be modeled using a normal distribution with mean 440 ml and standard deviation 10 ml; the amount of corn oil in each bottle of the blend can likewise be modeled using a normal distribution with mean 410 ml and standard deviation 15 ml. The amount of canola oil in each bottle is independent of the amount of corn oil.
(a) Determine the probability that the amount of oil in a randomly selected bottle of this blend will exceed 900 ml.
(b) Determine the probability that the amount of corn oil in a randomly selected bottle of this blend is greater than the amount of canola oil in the bottle.
(c) Based on your answer to part (b), what is the probability that, out of five randomly selected bottles of this blend, at least one of the bottles contains more corn oil than canola oil?
3. Salmon farmers have a choice of three different types of food (type A, type B, or type C) and two different breeds (Sockeye and Chinook). The salmon farmers want you to design an experiment in which you feed the different types of food to the two breeds of salmon to see which type of food leads to the largest salmon by weight. They provide you with 60 salmon divided equally between the two breeds and can provide you with up to 10 different tanks in which to raise the salmon. The farmers would like the results in 10 weeks.
(a) Design an appropriate experiment.
(b) Is your design single-blind, double-blind, or neither? Explain.
4. A nutritionist wants to confirm her suspicion that, among Americans, women tend to prefer chocolate for dessert more often than men. She decides that it will be convenient to collect data on customers of a large and popular restaurant owned by her family. The restaurant has a practice of showing the daily selection of desserts on a tray to the customers. For 500 customers selected randomly over a one-week period, the nutritionist notes the sex of the customer and the choice of dessert. The data is summarized in the table below.
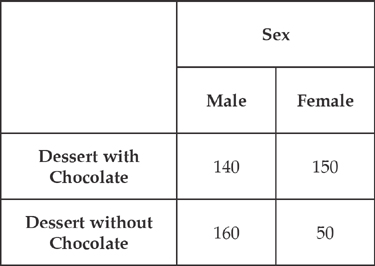
(a) Identify the target and sampled populations in this experiment. Are they the same or different? Discuss how their sameness or difference will affect the conclusions drawn from this experiment.
(b) The nutritionist is considering using a chi-square test of independence to analyze this data. Why is this test inappropriate to justify her suspicions?
(c) Which test would be more appropriate to gather evidence to support her suspicions? Can the test you named be done using this data? Justify your answer.
5. A large security-system management company with clients in Los Angeles and San Francisco installs and monitors security systems in houses and on business premises. The system’s alarm sounds at the central monitoring location if the system detects a security break-in, smoke, or fire at any of the clients’ premises. Tests have indicated that a false alarm occurs approximately 3 percent of the instances in which the alarm sounds, and that in approximately 0.5 percent of actual incidences, the system fails to sound an alarm. The records indicate that about 0.1 percent of its clients have break-in/fire/smoke incidents.
(a) Suppose a client is selected at random. What is the probability that the alarm will sound at this client’s premises?
(b) Suppose the alarm is sounded at a client’s premises. What is the probability that there was no break-in, smoke, or fire incident?
END OF PART A
STATISTICS
SECTION II
Part B
Question 6
Spend about 30 minutes on this part of the exam.
Percent of Section II grade—25
6. A physician who has delivered babies for over 20 years claims that birthweights of babies tend to be higher than the birthweight of their next older siblings. In other words, a parent’s second child tends to have a higher birthweight than the first child, the third child tends to have higher birthweight than the second child, and so on. To verify the doctor’s statement, her office assistant gets a random sample of mothers with at least two children from the hospital records, and records the birthweights of the first two children. The birthweights for the children of 19 mothers are given in the table below.
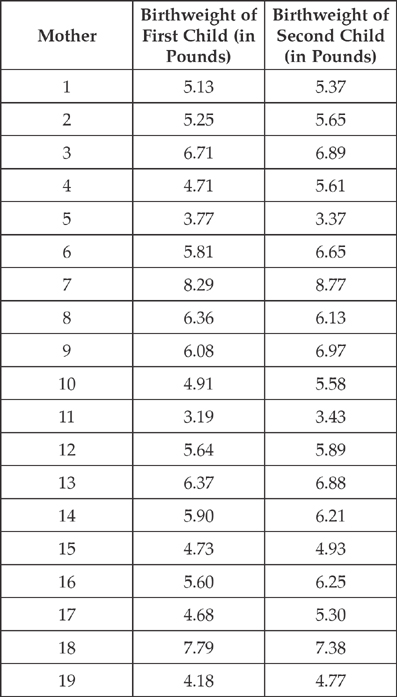
(a) Does this data provide any evidence to support the physician’s theory? Justify your answer using statistical evidence.
(b) The scatterplot of birthweights of first-born children and second-born children is given below.
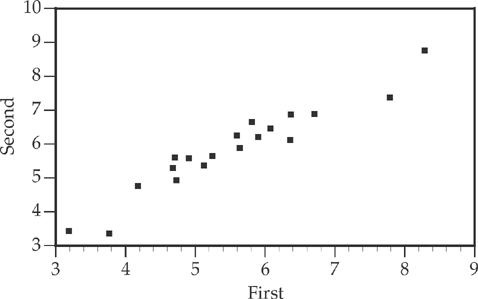
Describe the relation between the birthweights of first-born children and the birthweights of second-born children.
(c) The regression analysis of the data resulted in the following outcome.

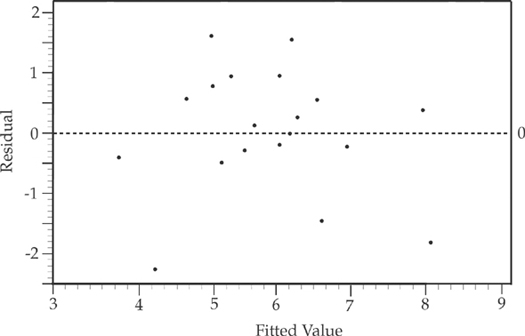
Is there a significant relation between the birthweights of first-born children and the birthweights of second-born children? Justify your answer using statistical evidence.
(d) Suppose the doctor is getting ready to deliver the second child of a mother whose first child weighed 7.2 pounds. Predict the birthweight of this second child.
(e) What is an approximate range of birthweights of second-born children whose first-born siblings weighed 7.2 pounds?
STOP
END OF EXAM