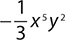In this chapter, you learn about polynomials. The chapter begins with a discussion of the elementary concepts that you need to know to ensure your success when working with polynomials and ends with addition and subtraction of polynomials.
Terms and Monomials
In an algebraic expression, terms are the parts of the expression that are connected to the other parts by indicated addition (plus sign) or indicated subtraction (minus sign). If the algebraic expression has no indicated addition or subtraction, then the algebraic expression itself is a term.
Problem
Identify the terms in the given expression.
a. 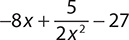
b. 3x5
Solution
a. 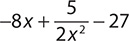

Step 1. The expression contains indicated addition and subtraction, so identify the quantities between the plus and minus signs.
The terms are −8x, 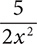 , and 27.
, and 27.
Step 1. There is no indicated addition or subtraction, so the expression is a term.
The term is 3 x5.
A monomial is a special type of term that, when simplified, is a constant or a product of one or more variables raised to nonnegative integer powers, with or without an explicit coefficient.
Problem
Specify whether the term is a monomial. Explain your answer.
a. 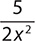
b. 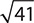
c. 0
d. 3x5
e. 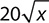
f. 4x-3y2
g. 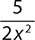
Solution
a. −8x

Step 1. Check whether −8x meets the criteria for a monomial.
-8x is a term that is a variable raised to a positive integer power of 1 (understood), with an explicit coefficient of −8, so it is a monomial.

Step 1. Check whether 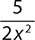 meets the criteria for a monomial.
meets the criteria for a monomial.
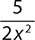 is a term, but it contains division by a variable, so it is not a monomial.
is a term, but it contains division by a variable, so it is not a monomial.
c. 0

Step 1. Check whether 0 meets the criteria for a monomial.
0 is a constant, so it is a monomial.

Step 1. Check whether 3x5 meets the criteria for a monomial.
3x5 is a term that is a variable raised to a positive integer power of 5, with an explicit coefficient of 3, so it is a monomial.
e. 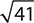

Step 1. Check whether 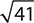 meets the criteria for a monomial.
meets the criteria for a monomial.
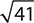 is a constant, so it is a monomial.
is a constant, so it is a monomial.
f. 4x-3y2

Step 1. Check whether 4x-3y2 meets the criteria for a monomial.
4x-3y2 contains a negative exponent, so it is not a monomial.
g. 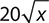

Step 1. Check whether 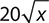 meets the criteria for a monomial.
meets the criteria for a monomial.
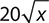 is a term, but it contains a variable as the radicand of a simplified radical, so it is not a monomial.
is a term, but it contains a variable as the radicand of a simplified radical, so it is not a monomial.
Polynomials
A polynomial consists of a single monomial or two or more monomials connected by plus or minus signs. A polynomial that has exactly one term is a monomial. A polynomial that has exactly two terms is a binomial. A polynomial that has exactly three terms is a trinomial. A polynomial that has more than three terms is just a general polynomial.
Problem
State the most specific name for the given polynomial.
a. x2-1
b. 8a3 + 64b3
c. x2 + 4x - 12
d. 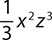
e. −2x5 + 5x4 - 3x3 - 7x2 + x + 4
a. x2-1

Step 1. Count the terms of the polynomial.
x2-1 has exactly two terms.
Step 2. State the specific name.
x2-1 is a binomial.
b. 8a3 + 64b3

Step 1. Count the terms of the polynomial.
8a3 + 64b3 has exactly two terms.
Step 2. State the specific name.
8a3 + 64b3 is a binomial.
c. x2 + 4x −12

Step 1. Count the terms of the polynomial.
x2 + 4x - 12 has exactly three terms.
Step 2. State the specific name.
x2 + 4x - 12 is a trinomial.
d. 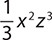

Step 1. Count the terms of the polynomial.
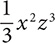 has exactly one term
has exactly one term
Step 2. State the specific name.
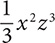 is a monomial.
is a monomial.
e. −2x5 + 5x4 - 3x3 - 7x2 + x + 4

Step 1. Count the terms of the polynomial.
-2x5 + 5x4 - 3x3 - 7x2 + x + 4 has exactly six terms.
Step 2. State the specific name.
-2x5 + 5x4 - 3x3 - 7x2 + x + 4 is a polynomial.
Like Terms
Monomials that are constants or monomials that have exactly the same variable factors (i.e., the same letters with the same corresponding exponents) are like terms. Like terms are the same except, perhaps, for their coefficients. Terms that are not like terms are unlike terms.
Problem
State whether the given monomials are like terms. Explain your answer.
a. −10x and 25x
b. 4x2y3 and −7x3y2
c. 100 and 45
d. 25 and 25x
Solution
a. −10x and 25x

Step 1. Check whether −10x and 25x meet the criteria for like terms.
-10x and 25x are like terms because they are exactly the same except for their numerical coefficients.
b. 4x2y3 and −7x3y2

Step 1. Check whether 4x2y3 and −7x3y2 meet the criteria for like terms.
4x2y3 and −7x3y2 are not like terms because the corresponding exponents on x and y are not the same.
c. 100 and 45

Step 1. Check whether 100 and 45 meet the criteria for like terms.
100 and 45 are like terms because they are both constants.
d. 25 and 25x

Step 1. Check whether 25 and 25x meet the criteria for like terms.
25 and 25x are not like terms because they do not contain the same variable factors.
Adding and Subtracting Monomials
Because variables are standing in for numbers, you rely on the properties of numbers to justify operations with polynomials. (See Chapter 1 for a discussion of the properties of numbers.)
 Addition and Subtraction of Monomials
Addition and Subtraction of Monomials
1. To add monomials that are like terms, add their numerical coefficients and use the sum as the coefficient of their common variable component.
2. To subtract monomials that are like terms, subtract their numerical coefficients and use the difference as the coefficient of their common variable component.
3. To add or subtract unlike terms, indicate the addition or subtraction.
Problem
Simplify.
a. −10x+ 25x
b. 4x2y3 - 7x3y2
c. 9x2 + 3x2 - 7x2
d. 25 + 25x
e. 5x2 - 7x2
Solution
a. −10x+ 25x

Step 1. Check for like terms.
-10x and 25x are like terms.
Step 2. Add the numerical coefficients.
-10 + 25 = 15
Step 3. Use the sum as the coefficient of x.
-10x + 25x = 15x
b. 4x2y3 - 7x3y2

Step 1. Check for like terms.
4x2y3 and 7x3y2 are not like terms, so leave the problem as indicated subtraction: 4x2y3 - 7x3y2.

Step 1. Check for like terms.
9x, 3x2, and 7x2 are like terms.
Step 2. Combine the numerical coefficients.
9 + 3 - 7 = 5
Step 3. Use the result as the coefficient of x2.
9x2 + 3x2 - 7x2 = 5x2
d. 25 + 25x

Step 1. Check for like terms.
25 and 25x are not like terms, so leave the problem as indicated addition: 25 + 25x.
e. 5x2 - 7x2

Step 1. Check for like terms.
5x2 and 7x2 are like terms.
Step 2. Subtract the numerical coefficients.
5 - 7 = −2
Step 3. Use the result as the coefficient of x2.
5x2 - 7x2 = −2x2
Simplifying Polynomial Expressions
When you have an assortment of like terms in the same expression, systematically combine matching like terms in the expression. (For example, you might proceed from left to right.) You are simplifying the expression when you do this. To organize the process, use the properties of numbers to rearrange the expression so that matching like terms are together (later, you might choose to do this step mentally). If the expression includes unlike terms, just indicate the sums or differences of such terms. To avoid sign errors as you work, keep a - symbol with the number that follows it.
Simplify.
a. 4x3 + 5x2 - 10x + 25 + 2x3 - 7x2 - 5
b. 5x - 20x + 30 - 10x + 100 + 3x - 25
Solution
a. 4x3 + 5x2 - 10x + 25 + 2x3 - 7x2 - 5

Step 1. Check for like terms.
The like terms are 4x3 and 2x3, 5x2 and 7x2, and 25 and 5.
Step 2. Rearrange the expression so that like terms are together.
4x3 + 5x2 - 10x + 25 + 2x3 - 7x2 - 5
= 4x3 + 2x3 + 5x2 - 7x2 - 10x + 25 - 5
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= 6x3 + −2x2 - 10x + 20
= 6x3 - 2x2 −10x + 20
Step 4. Review the main results.
4x3 + 5x2 - 10x + 25 + 2x3 - 7x2 - 5
= 4x3 + 2x3 + 5x2 - 7x2 - 10x + 25 - 5
= 6x3 - 2x2 - 10x + 20
b. 5x - 20x + 30 - 10x + 100 + 3x - 25

Step 1. Check for like terms.
The like terms are 5x, 20x, 10x, and 3x and 30, 100, and 25.
Step 2. Rearrange the expression so that like terms are together.
5x - 20x + 30 - 10x + 100 + 3x - 25
= 5x - 20x - 10x + 3x + 30 + 100 - 25
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= −22x +105
Step 4. Review the main results.
5x - 20x + 30 - 10x + 100 + 3x - 25
= 5x - 20x - 10x + 3x + 30 + 100 - 25
= −22x + 105
Adding Polynomials
Addition of polynomials involves adding like terms.
 Addition of Polynomials
Addition of Polynomials
To add two or more polynomials, add like monomial terms and simply indicate addition of unlike terms.
Problem
Perform the indicated addition.
a. (9x2 - 6x + 2) + (-7x2 - 5x + 3)
b. (4x3 + 3x2 - x + 8) + (8x3 + 2x - 10)
Solution
a. (9x2 - 6x + 2) + (-7x2 - 5x + 3)

Step 1. Remove parentheses.
(9x2 - 6x + 2) + ( 7x2 - 5x + 3)
= 9x2 - 6x + 2 - 7x2 - 5x + 3
Step 2. Rearrange the terms so that like terms are together. (You may do this step mentally.)
= 9x2 - 7x2 - 6x - 5x + 2 + 3
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= 2x2 −11 x + 5
Step 4. Review the main results.
(9x2 - 6x + 2) + (-7x2 - 5x + 3)
= 9x2 - 6x + 2 - 7x2 - 5x + 3
= 9x2 - 7x2 - 6x - 5x + 2 + 3
= 2x2 - 11x + 5
b. (4x3 + 3x2 - x + 8) + (8x3 + 2x - 10)

Step 1. Remove parentheses.
(4x3 + 3x2 - x + 8) + (8x3 + 2x - 10)
= 4x3 + 3x2 - x + 8 + 8x3 + 2x - 10
Step 2. Rearrange the terms so that like terms are together. (You may do this step mentally.)
= 4x3 + 8x3 + 3x2 - x + 2x + 8 - 10
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= 12x3 + 3x2 + x - 2
Step 4. Review the main results.
(4x3 + 3x2 - x + 8) + (8x3 + 2x - 10)
= 4x3 + 3x2 - x + 8 + 8x3 + 2x - 10
= 4x3 + 8x3 + 3x2 - x + 2x + 8 - 10
= 12x3 + 3x2 + x - 2
Subtracting Polynomials
Subtraction of polynomials relies on your skills in adding polynomials.
Subtraction of Polynomials
To subtract two polynomials, add the opposite of the second polynomial.
You can accomplish subtraction of polynomials by enclosing both polynomials in parentheses and then placing a minus symbol between them. Of course, make sure that the minus symbol precedes the polynomial that is being subtracted.
Problem
Perform the indicated subtraction.
a. (9x2 - 6x + 2) - (-7x2 - 5x + 3)
b. (4x3 + 3x2 - x + 8) - (8x3 + 2x - 10)
a. (9x2 - 6x + 2) - (-7x2 - 5x + 3)

Step 1. Remove parentheses.
(9x2 - 6x + 2) - (-7x2 - 5x + 3)
= 9x2 - 6x + 2 + 7x2 + 5x - 3
Step 2. Rearrange the terms so that like terms are together. (You may do this step mentally.)
= 9x2 + 7x2 - 6x + 5x + 2 - 3
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= 16x2 - x - 1
Step 4. Review the main results.
(9x2 - 6x + 2) - (-7x2 - 5x + 3)
= 9x2 - 6x + 2 + 7x2 + 5x - 3
= 9x2 + 7x2 - 6x + 5x + 2 - 3
= 16 x2 - x - 1
b. (4x3 + 3x2 - x + 8) - (8x3 + 2x - 10)

Step 1. Remove parentheses.
(4x3 + 3x2 - x + 8) - (8x3 + 2x - 10)
= 4x3 + 3x2 - x + 8 - 8x3 - 2x + 10
Step 2. Rearrange the terms so that like terms are together. (You may do this step mentally.)
= 4x3 - 8x3 + 3x2 - x - 2x + 8 + 10
Step 3. Systematically combine matching like terms and indicate addition or subtraction of unlike terms.
= −4x3 + 3x2 - 3x + 18
Step 4. Review the main results.
(4x3 + 3x2 - x + 8) - (8x3 + 2x - 10)
= 4x3 + 3x2 - x + 8 - 8x3 - 2x + 10
= 4x3 - 8x3 + 3x2 - x - 2x + 8 + 10
= −4x3 + 3x2 - 3x + 18
 Exercise 13
Exercise 13
For 1-5, state the most specific name for the given polynomial.
1. x2 - x + 1
2. 125x3 - 64y3
3. 2x2 + 7x - 4
5. 2x4 + 3x3 - 7x2 - x + 8
For 6-15, simplify.
6. −15x + 17x
7. 14xy3 - 7x3y2
8. 10x2 - 2x2 - 20x2
9. 10 + 10x
10. 2 + 4(x + 5)
11. 12x3 - 5x2 + 10x - 60 + 3x3 - 7x2 - 1
12. (10x2 - 5x + 3) + (6x2 + 5x - 13)
13. (20x3 - 3x2 - 2x + 5) + (9x3 + x2 + 2x - 15)
14. (10x2 - 5x + 3) - (6x2 + 5x - 13)
15. (20x3 - 3x2 - 2x + 5) - (9x3 + x2 + 2x - 15)
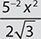 is a monomial.
is a monomial.