19

Mean, Median, Mode, and Range

In this chapter, you learn how to calculate the mean, median, mode, and range for a set of numbers. The mean, median, and mode are measures of central tendency. A measure of central tendency is a numerical value that describes a set of numbers (such as students’ scores on a test) by attempting to provide a “central” or “typical” value of the numbers. The range is a measure of variability. It gives you an idea of the spread of a set of numbers.

Mean

The mean of a set of numbers is another name for the arithmetic average of the numbers in the set. To calculate the mean: first, sum the numbers; then, divide by how many numbers are in the set. Thus, you have the following formula:

Remember that the fraction bar indicates division.

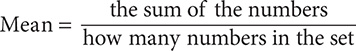
Problem

Find the mean for the given set of numbers.

a. {25, 43, 40, 60, 12}

b. {−7, 22, −7, 8, 16, 1}

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

d. {0, 0, 0, 100, 100, 100}

e. {50, 50, 50, 50, 50, 50, 50}

f. {−70, −60, −50, −50, −40, −30}

The braces around a list of numbers mean that the numbers belong together as a set. You read {1,3,5} as “the set consisting of the numbers 1, 3, and 5.”

Solution

a. {25, 43, 40, 60, 12}

Step 1.   Sum the numbers.

25 + 43 + 40 + 60 + 12 = 180

When computing a mean, don’t forget to divide by how many numbers you have.

Step 2.   Divide by 5.

Step 3.   State the answer.

The mean is 36.

If all the numbers are positive, then the mean of the numbers is also positive.

b. {−7, 22, −7, 8, 16, 1}

Step 1.   Sum the numbers.

-7 + 22 - 7 + 8 + 16 + 1 = 33

Step 2.   Divide by 6.

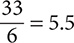
Step 3.   State the answer.

The mean is 5.5.

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

Step 1.   Sum the numbers.

6.7 + 7.6 + 7.5 + 6.9 + 9.3 + 6.7 + 7.6 + 8.5 = 60.8

Step 2.   Divide by 8.

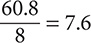
Step 3.   State the answer.

The mean is 7.6.

d. {0, 0, 0, 100, 100, 100}

Step 1.   Sum the numbers.

0 + 0 + 0 + 100 + 100 + 100 = 300

Step 2. Divide by 6.

When you compute a mean, you divide by how many numbers you have, including the number of zeros, if any. Don’t forget to count the zeros.

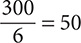
Step 3.   State the answer.

The mean is 50.

e. {50, 50, 50, 50, 50, 50, 50}

Step 1.   Sum the numbers.

50 + 50 + 50 + 50 + 50 + 50 + 50 = 350

Step 2.   Divide by 7.

As you might expect, if all the numbers are the same, the mean of the numbers is the common number.

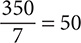
Step 3.   State the answer.

The mean is 50.

f. {−70, −60, −50, −50, −40, −30}

Step 1.   Sum the numbers.

- 70 - 60 - 50 - 50 - 40 - 30 = −300

Step 2.   Divide by 6.

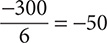
Step 3.   State the answer.

The mean is −50.

If all the numbers are negative, then the mean of the numbers is also negative.

Weighted Average

A weighted average (or weighted mean) is an average computed by assigning weights to the numbers (e.g., test scores).

Problem

A student scores 50, 40, and 96 on three exams. Find the weighted average of the student’s three scores, where the score of 50 counts 20%, the score of 40 counts 30%, and the score of 96 counts 50%.

Solution

Step 1.   Multiply each score by its corresponding “weight” and then add.

20%(50) + 30%(40) + 50%(96) = 0.2(50) + 0.3(40) + 0.5(96) = 70

Step 2.   Sum the weights.

20% + 30% + 50% = 100% = 1

Step 3.   Divide the sum in step 1 by the sum in step 2.

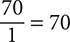
Step 4.   State the answer.

The student’s weighted average is 70.

Median

The median is the middle value or the arithmetic average of the two middle values in an ordered set of numbers. To find the median, do the following:

1. Put the numbers in order from least to greatest (or greatest to least).

2. Locate the middle number. If there is no single middle number, compute the arithmetic average of the two middle numbers.

Problem

Find the median.

a. {25, 43, 40, 60, 12}

b. {−7, 22, −7, 8, 16, 1}

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

d. {0, 0, 0, 100, 100, 100}

e. {50, 50, 50, 50, 50, 50, 50}

f. {−70, −60, −50, −50, −40, −30}

Solution

a. {25, 43, 40, 60, 12}

Step 1.   Put the numbers in order from least to greatest.

12, 25, 40, 43, 60

Step 2. Locate the middle number.

40 is the middle number.

Step 3.   State the answer.

The median is 40.

b. {−7, 22, −7, 8, 16, 1}

Step 1.   Put the numbers in order from least to greatest.

-7, −7, 1, 8, 16, 22

Step 2.   Locate the middle number.

There is no single middle number, so compute the arithmetic average of the two middle numbers, 1 and 8.

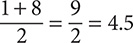
Step 3.   State the answer.

The median is 4.5.

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

Step 1.   Put the numbers in order from least to greatest.

6.7, 6.7, 6.9, 7.5, 7.6, 7.6, 8.5, 9.3

Step 2.   Locate the middle number.

There is no single middle number, so compute the arithmetic average of the two middle numbers, 7.5 and 7.6.

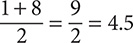
Step 3.   State the answer.

The median is 7.55.

d. {0, 0, 0, 100, 100, 100}

Step 1.   Put the numbers in order from least to greatest.

0, 0, 0, 100, 100, 100

Step 2. Locate the middle number.

There is no single middle number, so compute the arithmetic average of the two middle numbers, 0 and 100.

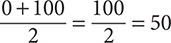
Step 3.   State the answer.

The median is 50.

e. {50, 50, 50, 50, 50, 50, 50}

Step 1.   Put the numbers in order from least to greatest.

50, 50, 50, 50, 50, 50, 50

Step 2.   Locate the middle number.

The middle number is 50.

As with the mean, if all the numbers are the same, the median of the numbers is the common number.

Step 3.   State the answer.

The median is 50.

f. {−70, −60, −50, −50, −40, −30}

Step 1.   Put the numbers in order from least to greatest.

-70, −60, −50, −50, −40, −30

Step 2.   Locate the middle number.

There is no single middle number, so compute the arithmetic average of the two middle numbers, −50 and −50.

If the two middle numbers are the same, then the arithmetic average is the common number.

Step 3.   State the answer.

The median is −50.

As with the mean, if all the numbers are negative, then the median of the numbers is also negative.

Mode

In a set of numbers, the mode is the number (or numbers) that occurs most often (i.e., with the greatest frequency). A set of numbers in which each number occurs the same number of times has no mode. If only one number occurs most often, then the set is unimodal. If exactly two numbers occur with the same frequency that is more often than any of the other numbers, then the set is bimodal. If three or more numbers occur with the same frequency that is more often than any of the other numbers, then the set is multimodal.

Problem

Find the mode, if any. For number sets that have modes, state whether the data set is unimodal, bimodal, or multimodal.

a. {25, 43, 40, 60, 12}

b. {−7, 22, −7, 8, 16, 1}

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

d. {0, 0, 0, 100, 100, 100}

e. {50, 50, 50, 50, 50, 50, 50}

f. {−70, −60, −50, −50, −40, −30}

Solution

a. {25, 43, 40, 60, 12}

Step 1.   For each number, determine how often it occurs.

Each number occurs only once.

Step 2.   State the mode, if any.

There is no mode.

b. {−7, 22, −7, 8, 16, 1}

Step 1.   For each number, determine how often it occurs.

The numbers 1, 8, 16, and 22 each occur only once.

The number −7 occurs twice.

Step 2.   State the mode, if any.

The mode is −7, so the set is unimodal.

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

Step 1.   For each number, determine how often it occurs.

The numbers 6.9, 7.5, 8.5, and 9.3 each occur only once.

The numbers 6.7 and 7.6 each occur twice.

Step 2. State the mode, if any.

The modes are 6.7 and 7.6, so the set is bimodal.

d. {0, 0, 0, 100, 100, 100}

Step 1.   For each number, determine how often it occurs.

The numbers 0 and 100 each occurs three times.

Step 2.   State the mode, if any.

The modes are 0 and 100, so the set is bimodal.

e. {50, 50, 50, 50, 50, 50, 50}

Step 1.   For each number, determine how often it occurs.

The number 50 occurs seven times.

Step 2.   State the mode, if any.

The mode is 50, so the set is unimodal.

f. {−70, −60, −50, −50, −40, −30}

Step 1.   For each number, determine how often it occurs.

The numbers −70, −60, −40, and-30 each occur only once.

The number −50 occurs twice.

Step 2.   State the mode, if any.

The mode is −50, so the set is unimodal.

Range

The range describes the spread of a set of numbers. You find the range by computing the difference between the greatest number and the least number; that is,

The range of a set of numbers is always nonnegative.

Range = greatest number - least number

Problem

Find the range.

a. {25, 43, 40, 60, 12}

b. {−7, 22, −7, 8, 16, 1}

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

d. {0, 0, 0, 100, 100, 100}

e. {50, 50, 50, 50, 50, 50, 50}

f. {−70, −60, −50, −50, −40, −30}

Solution

a. {25, 43, 40, 60, 12}

Step 1.   Identify the greatest number and the least number.

60 is the greatest number, and 12 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = 60 - 12 = 48

Step 3.   State the answer.

The range is 48.

b. {−7, 22, −7, 8, 16, 1}

Step 1.   Identify the greatest number and the least number.

22 is the greatest number, and −7 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = 22 - (-7) = 22 + 7 = 29

Step 3.   State the answer. The range is 29.

c. {6.7, 7.6, 7.5, 6.9, 9.3, 6.7, 7.6, 8.5}

Step 1.   Identify the greatest number and the least number.

9.3 is the greatest number, and 6.7 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = 9.3 - 6.7 = 2.6

Step 3.   State the answer.

The range is 2.6.

d. {0, 0, 0, 100, 100, 100}

Step 1.   Identify the greatest number and the least number.

100 is the greatest number, and 0 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = 100 - 0 = 100

Step 3.   State the answer.

The range is 100.

e. {50, 50, 50, 50, 50, 50, 50}

Step 1.   Identify the greatest number and the least number.

50 is the greatest number, and 50 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = 50 - 50 = 0

If all the numbers are the same, then the range of the numbers is 0.

Step 3.   State the answer.

The range is 0.

f. {−70, −60, −50, −50, −40, −30}

Step 1.   Identify the greatest number and the least number.

-30 is the greatest number, and −70 is the least number.

Step 2.   Compute the range.

range = greatest number - least number = −30 - (-70) = −30 + 70 = 40

Step 3.   State the answer.

The range is 40.

Exercise 19

For 1-4, find the mean.

1. {15, 33, 30, 50, 0}

2. {−4, 25, −4, 11, 19, 4}

3. {4.7, 5.6, 2.5, 4.9, 7.3, 4.7, 5.6, 6.5}

4. {−10, 0, 3, 3, 6, 16}

5. A student scores 80, 90, and 70 on three exams. Find the weighted average of the student’s three scores, where the score of 80 counts 10%, the score of 90 counts 30%, and the score of 70 counts 60%.

For 6-10, find the median.

6. {15, 33, 30, 50, 0}

7. {−4, 25, −4, 11, 19, 4}

8. {4.7, 5.6, 2.5, 4.9, 7.3, 4.7, 5.6, 6.5}

9. {−10, 0, 3, 3, 6, 16}

10. {1, 1, 4, 4, 4, 10, 10, 10}

For 11-15, find the mode, if any. For number sets that have modes, state whether the set is unimodal, bimodal, or multimodal.

11. {15, 33, 30, 50, 0}

12. {−4, 25, −4, 11, 19, 4}

13. {4.7, 5.6, 2.5, 4.9, 7.3, 4.7, 5.6, 6.5}

14. {−10, 0, 3, 3, 6, 16}

15. {1, 1, 4, 4, 4, 10, 10, 10}

For 16-20, find the range.

16. {15, 33, 30, 50, 0}

17. {−4, 25, −4, 11, 19, 4}

18. {4.7, 5.6, 2.5, 4.9, 7.3, 4.7, 5.6, 6.5}

19. {−10, 0, 3, 3, 6, 16}

20. {150, 330, 300, 500, 0}