© International Association for Cryptologic Research 2020
R. Pass, K. Pietrzak (eds.)Theory of CryptographyLecture Notes in Computer Science12552https://doi.org/10.1007/978-3-030-64381-2_1

Universal Composition with Global Subroutines: Capturing Global Setup Within Plain UC

Christian Badertscher1  , Ran Canetti2  , Julia Hesse3  , Björn Tackmann4   and Vassilis Zikas5  
(1)
IOHK, Zurich, Switzerland
(2)
Boston University, Boston, MA, USA
(3)
IBM Research, Zurich, Switzerland
(4)
DFINITY, Zurich, Switzerland
(5)
University of Edinburgh, Edinburgh, UK
 
 
Christian Badertscher (Corresponding author)
Email: christian.badertscher@iohk.io
 
Ran Canetti
Email: canetti@bu.edu
 
Julia Hesse
Email: jhs@zurich.ibm.com
 
Björn Tackmann
Email: bjoern@dfinity.org
 
Vassilis Zikas
Email: vzikas@inf.ed.ac.uk

Abstract

The Global and Externalized UC frameworks [Canetti-Dodis-Pass-Walfish, TCC 07] extend the plain UC framework to additionally handle protocols that use a “global setup”, namely a mechanism that is also used by entities outside the protocol. These frameworks have broad applicability: Examples include public-key infrastructures, common reference strings, shared synchronization mechanisms, global blockchains, or even abstractions such as the random oracle. However, the need to work in a specialized framework has been a source of confusion, incompatibility, and an impediment to broader use.

We show how security in the presence of a global setup can be captured within the plain UC framework, thus significantly simplifying the treatment. This is done as follows:

  • We extend UC-emulation to the case where both the emulating protocol $$\pi $$ and the emulated protocol $$\phi $$ make subroutine calls to protocol $$\gamma $$ that is accessible also outside $$\pi $$ and $$\phi $$. As usual, this notion considers only a single instance of $$\phi $$ or $$\pi $$ (alongside $$\gamma $$).

  • We extend the UC theorem to hold even with respect to the new notion of UC emulation. That is, we show that if $$\pi $$ UC-emulates $$\phi $$ in the presence of $$\gamma $$, then $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$ for any protocol $$\rho $$, even when $$\rho $$ uses $$\gamma $$ directly, and in addition calls many instances of $$\phi $$, all of which use the same instance of $$\gamma $$. We prove this extension using the existing UC theorem as a black box, thus further simplifying the treatment.

We also exemplify how our treatment can be used to streamline, within the plain UC model, proofs of security of systems that involve global set-up, thus providing greater simplicity and flexibility.

1 Introduction

Modular security analysis of cryptographic protocols calls for an iterative process, where in each iteration the analyst first partitions the given system into basic functional components, then separately specifies the security properties of each component, then demonstrates how the security of the overall system follows from the security of the components, and then proceeds to further partition each component. The key attraction here is the potential ability to analyze the security of each component once, in a simplified “in vitro” setting, and then re-use the asserted security guarantees in the various contexts in which this component is used.

A number of analytical frameworks have been devised over the years with this goal in mind, e.g. [MR91, Bea91, HM97, Can00, PW00, Can01, BPW04, Mau11, KMT20, HS16, CKKR19]. These frameworks allow representing protocols, tasks, and attacks, and also offer various composition operations and associated security-preserving composition theorems that substantiate the above analytical process. The overarching goal here is to have an analytical framework that is as expressive as possible, and at the same time allows for a nimble and effective de-compositional analytical process.

Modularity in these frameworks is obtained as follows. (We use here the terminology of the UC framework [Can01], but so far the discussion applies to all these frameworks.) We first define when a protocol $$\pi $$ “emulates” another protocol $$\phi $$. Ideally, this definition should consider a setting with only a single instance of $$\pi $$ (or $$\phi $$) and no other protocols. A general composition theorem then guarantees that if $$\pi $$ emulates protocol $$\phi $$, then for any protocol $$\rho $$, that makes “subroutine calls” to potentially multiple instances of $$\phi $$, the protocol $$\rho ^{\phi \rightarrow \pi }$$ emulates $$\rho $$, where $$\rho ^{\phi \rightarrow \pi }$$ is the protocol that is essentially identical to $$\rho $$ except that each subroutine call to an instance of $$\phi $$ is replaced with a subroutine call to an instance of $$\pi $$.

This composition theorem is indeed a powerful tool: It allows analyzing a protocol in a highly simplified setting that involves only a single instance of the protocol and no other components, and then deducing security in general multi-component systems. However, the general composition theorem can only be applied when protocols $$\pi $$ and $$\phi $$ do not share any “module” with the calling protocol, $$\rho $$. That is, the theorem applies only when there is no module, or protocol, $$\gamma $$, such that $$\gamma $$ is a subroutine of $$\pi $$ or $$\phi $$, and at the same time $$\gamma $$ is used directly as a subroutine of $$\rho $$. Furthermore, when $$\rho $$ calls multiple instances of $$\phi $$, no module $$\gamma $$ can be a subroutine of two different instances of $$\phi $$.

This limitation has proven to be a considerable impediment when coming to analyze realistic systems, and in particular when trying to de-compose such system to smaller components as per the above methodology. Indeed, realistic systems often include some basic components that require trust in external entities or are expensive to operate. It then makes sense to minimize the number of such components and have them shared by as many other components as possible. Examples for such shared components include public-key infrastructure, long-lived signing modules, shared synchronization and timing mechanisms, common reference strings, and even more complex constructs such as blockchains and public repositories.

Overcoming this limitation turns out to take quite different forms, depending on the underlying model of computation. When the model of computation is static, namely the identities, programs, and connectivity graph of computing elements are fixed throughout the computation, extending the basic composition theorem to account for shared (or, “global”) subroutines is relatively straightforward. (Examples include the restricted model of [Can20, Section 2], as well as [BPW07, KMT20].) However, restricting ourselves to a static model greatly limits the applicability of the framework, and more importantly the power of the composition theorem. Indeed, static models are not conducive to capturing prevalent situations where multiple instances of a simple protocol are invoked concurrently and dynamically, and where all sessions share some global infrastructure; examples include secure communication sessions, payment protocols, cryptocurrencies, automated contracts.

In order to be able to benefit from compositional analysis with shared modules even when the analyzed protocols are dynamic in nature, new composition theorems and frameworks were formulated, such as the Joint-State UC (JUC) theorem [CR03] and later the Generalized UC (GUC) and Extended UC (EUC) models [CDPW07].

However the GUC modeling is significantly more complex than the plain UC model. Furthermore, the extended model needs to be used throughout the analysis, even in parts that are unrelated to the global subroutine. In particular, working in the GUC model requires directly analyzing a protocol in a setting where it runs alongside other protocols. This stands in contrast to the plain UC model of protocol execution, which consists only of a single instance of the analyzed protocol, and no other “moving parts.” Additionally, while the basic UC framework has been updated and expanded several times in recent years, the GUC model has not been updated since its inception. Furthermore, the claimed relationship between statements made in the EUC framework and statements made in the GUC framework has some apparent inaccuracies.1

Our Contribution. We simplify the treatment of universal composition with global subroutines for fully dynamic protocols. Specifically, We show how to capture GUC-emulation with respect to global subroutines, and provide a theorem akin to the GUC theorem, all within the plain UC modeling. This theorem, which we call the Universal Composition with Global Subroutines (UCGS) theorem, allows for fully reaping all the (de-)compositional benefits of the GUC modeling, while keeping the model simple, minimizing the formalism, and enabling smooth transition between components.

We present our results in two steps. First, we present the modeling and theorem within the restricted model of computation of [Can20, Section 2]. Indeed, here the GUC and UCGS modeling is significantly less expressive - but it introduces the basic approach, and is almost trivial to formulate and prove. Next we explain the challenges involved in applying this approach to the full-fledged UC framework, and describe how we handle them. This is where most of the difficulty - and benefit - of this work lies.

Let us first briefly recall UC security within that restricted model. The model postulates a static system where the basic computing elements (called machines) send information to each other via fixed channels (or, ports). That is, machines have unique identities, and each machine has a set of machine identities with which it can communicate. Within each machine, each channel is labeled as either input or output. A system is a collection of machines where the communication sets are globally consistent, namely if machine M can send information to machine $$M'$$ with channel labeled input (resp., output) then the system contains a machine $$M'$$ that can send information labeled output (resp., input) to M. In this case we say that $$M'$$ is a subroutine (resp., caller) of M.

A protocol is a set $$\pi $$ of machines with consistent labeling as above, except that some machines in $$\pi $$ may have output channels to machines which are not part of $$\pi $$. These channels are the external channels of $$\pi $$. The machines in $$\pi $$ that have external channels are called the top level machines of $$\pi $$.

An execution of a protocol $$\pi $$ with an environment machine $$\mathcal {Z} $$ and an adversary machine $$\mathcal {A} $$ is an execution of the system that consists of $$(\pi \cup \{\mathcal {Z} ,\mathcal {A} \})$$, where the external channels of $$\pi $$ are connected to $$\mathcal {Z} $$, and $$\mathcal {A} $$ is connected to all machines in the system via a channel (port) named backdoor. The execution starts with an activation of $$\mathcal {Z} $$ and continues via a sequence of activations until $$\mathcal {Z} $$ halts with some binary decision value. Let ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq64_HTML.gif denote the random variable describing the decision bit of $$\mathcal {Z} $$ following an execution with $$\pi $$ and $$\mathcal {A} $$. 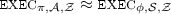We say that protocol $$\pi $$ UC-emulates protocol $$\phi $$ if for any polytime adversary $$\mathcal {A} $$ there exists a polytime adversary $$\mathcal {S} $$ such that for any polytime $$\mathcal {Z} $$ we have ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq73_HTML.gif.

The universal composition operation in this model is a simple machine replacement operation: Let $$\rho $$ be a protocol, let $$\phi $$ be a subset of the machines in $$\rho $$ that is a protocol in and of itself, and let $$\pi $$ be a protocol that has the same set of external identities as $$\phi $$, and where $$\pi $$ and $$\rho \setminus \phi $$ are identity-disjoint, i.e. the identities of the machines in $$\pi $$ are disjoint from the identities of the machines in $$\rho \setminus \phi $$. Then the composed protocol $$\rho ^{\phi \rightarrow \pi }$$ is defined as $$(\rho \setminus \phi )\cup \pi $$. The UC theorem states that if $$\pi $$ UC-emulates $$\phi $$, then for any $$\rho $$ such that $$\pi $$ and $$\rho \setminus \phi $$ are identity-disjoint we have that $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$. (Notice that here the UC operation replaces only a single “protocol instance”. Indeed, here there is no natural concept of “multiple instances” of a protocol.)

In this restricted model, protocol $$\gamma $$ is a global subroutine of a protocol $$\pi '$$ if $$\gamma $$ is a subroutine of $$\pi '$$, and at the same time some of the top level machines of $$\pi '$$ are actually in $$\gamma $$. Said otherwise, $$\pi '$$ consists of two parts, $$\gamma $$ and $$\pi =\pi '\setminus \gamma $$, where both $$\pi $$ and $$\gamma $$ include machines that take inputs directly from outside $$\pi '$$, and in addition some machines in $$\gamma $$ take inputs also from machines in $$\pi $$. Observe that this structure allows $$\gamma $$ to be a subroutine also of protocols other than $$\pi $$.

The Universal Composition with Global Subroutines (UCGS) theorem for such protocols takes the following form: Let $$\rho $$, $$\pi $$, $$\phi $$ and $$\gamma $$ be such that $$\pi '=\pi \cup \gamma $$ and $$\phi '=\phi \cup \gamma $$ are protocols where $$\pi '$$ UC-emulates $$\phi '$$ (and in addition $$\pi $$ and $$\rho \setminus \phi $$ are identity-disjoint). Then the protocol $$((\rho \setminus \phi ')\cup \pi ')$$ UC-emulates $$\rho $$. Observe, however, that in this model the UCGS theorem follows immediately from the standard UC theorem: Indeed, $$(\rho \setminus \phi ')\cup \pi '=(\rho \setminus \phi )\cup \pi =\rho ^{\phi \rightarrow \pi }$$. See illustration in Fig. 1.
../images/508076_1_En_1_Chapter/508076_1_En_1_Fig1_HTML.png
Fig. 1.

UC with Global Subroutines (UCGS) in the restricted setting of [Can20, Section 2]: Protocol $$\gamma $$ is a global subroutine of protocol $$\pi '$$ if $$\gamma $$ takes input from $$\pi =\pi '\setminus \gamma $$ and also from outside $$\pi '$$. Then plain UC theorem already guarantees that if $$\pi '$$ UC-realizes protocol $$\phi '$$, where $$\phi '=\phi \cup \gamma $$, then for any $$\rho $$ that calls $$\phi $$ and $$\gamma $$, the protocol $$((\rho \setminus \phi )\cup \pi )=\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$.

Extending the Treatment to the Full-Fledged UC Framework. While formulating UC with global subroutines within the above basic model is indeed simple, it is also of limited applicability: While it is in principle possible to use security in this model to infer security in systems that involve multiple instances of the analyzed protocol, inference is still limited to static systems where all identities and connectivity is fixed beforehand. The formalism breaks down when attempting to express systems where connectivity is more dynamic in nature, as prevalent in reality. In order to handle such situations, the full-fledged UC framework has a very different underlying model of distributed computation, allowing machines to form communication patterns and generate other machines in a dynamic way throughout the computation. Crucially, even in dynamic and evolving systems, the framework allows delineating those sets of processes that make up “protocol instances,” and then allows using single-instance-security of protocols to deduce security of the entire system.

To gain this level of expressiveness, the framework introduces a number of constructs. One such construct is the introduction of the session identifier (SID) field, that allows identifying the machines (processes) in a protocol instance. Specifically, an instance (or, session) of a protocol $$\pi $$ with SID s, at a given point during an execution of a system is the set of machines that have program $$\pi $$ and SID s. The extended session of $$\pi $$ with SID s consists of the machines of this session, their subroutines, and the transitive closure of all the machines that were created by the these subroutines during the execution so far. Another added construct is the concept of subroutine respecting protocols. Informally, protocol $$\pi $$ is subroutine respecting if, in any extended session s of $$\pi ,$$ the only machines, that provide output to, or responds to inputs from, machines outside this extended instance, are the actual “main” machines of this instance (namely the machines with code $$\pi $$ and SID s). Machines in the extended session, which are not the main machines, only take input from and provide output to other machines of this extended instance.

While the SIDs and the restriction to subroutine respecting protocols are key to the ability of the UC framework to model prevalent dynamic situations, they appear to get in the way of the ability to prove UC with global subroutines. In particular, simply applying the UC theorem as in the basic model is no longer possible. Indeed (referring to Fig. 1), neither $$\pi $$ nor $$\phi $$ are subroutine respecting, and the constructs $$\pi '$$ and $$\phi '$$, which were legitimate protocols in the basic model, are not legitimate protocols in the full-fledged model, since they don’t have the same program or SID. Note that this is not just a technicality: In a dynamically evolving system with multiple instances of $$\pi $$ and $$\gamma $$ there can be many possible ways of delineating protocol instances, and so the composition theorem may not even be well-defined!

We get around this barrier by providing a mechanism for encapsulating an instance of $$\phi $$ and one (or more) instances of $$\gamma $$ within a single “transparent envelope protocol” $$\mathsf {M}[\phi ,\gamma ]$$ such that a single instance of $$\mathsf {M}[\phi ,\gamma ]$$ has the same effect as the union of the instance of $$\phi $$ and the instances of $$\gamma $$ used by this instance of $$\phi $$. To accomplish that, we extend the shell and body mechanism that’s already used in the UC framework to enforce subroutine respecting behavior and to implement the UC operation. A similar encapsulation is done for $$\pi $$ and $$\gamma $$. Furthermore, the transformation guarantees that both $$\mathsf {M}[\phi ,\gamma ]$$ and $$\mathsf {M}[\pi ,\gamma ]$$ are now subroutine respecting, even though neither $$\phi $$ nor $$\pi $$ are. This enables us to invoke the UC theorem (this time in the full-fledged UC model) to obtain our main result:

Main Theorem (Informal). Assume $$\pi ,\phi ,\gamma $$are such that $$\mathsf {M}[\pi ,\gamma ]$$UC-emulates $$\mathsf {M}[\phi ,\gamma ]$$ . Then for (essentially) any protocol $$\rho $$we have that $$\rho ^{\phi \rightarrow \pi }$$UC-emulates $$\rho $$.

Our result follows the spirit of the UC theorem: It allows using the security of a single instance of $$\pi $$ (in the presence of $$\gamma $$) to deduce security of a system that involves multiple instances of $$\pi $$ (again, in the presence of $$\gamma $$). Said otherwise, the theorem allows dissecting a complex, dynamic, multi-instance system into simple, individual components, analyze the security of a single instance of a component, and deduce security of the overall system - even in the prevalent cases where multiple (or even all) of the individual components are using the same global subroutines. See depiction in Fig. 2.

We prove the new composition theorem in a modular way. That is, our proof makes black-box use of the plain UC theorem, thus avoiding the need to re-prove it from scratch, as in the GUC and EUC modeling.
../images/508076_1_En_1_Chapter/508076_1_En_1_Fig2_HTML.png
Fig. 2.

UC with global subroutines in the full-fledged UC framework: We encapsulate a single instance of $$\pi $$ plus one or more instances of $$\gamma $$ within a single instance of a protocol $$\mathsf {M}[\pi ,\gamma ]$$ that remains transparent to $$\pi $$ and $$\gamma $$ and is in addition subroutine respecting. We then show that if $$\mathsf {M}[\pi ,\gamma ]$$ UC-emulates $$\mathsf {M}[\pi ,\phi ]$$ then the protocol $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$ for essentially any $$\rho $$—even when $$\rho $$ and all the instances of $$\phi $$ (resp., $$\pi $$) use the same global instances of $$\gamma $$.

Demonstrating the Use of Our Treatment. We showcase our UCGS theorem in two settings. A first setting is that of analyzing the security of signature-based authentication and key exchange protocols in a setting where the signature module is global and in particular shared by multiple instances of the authentication module, as well as by arbitrary other protocols. This setting was studied in [CSV16] within the GUC framework. We demonstrate how our formalism and results can be used to cast the treatment of [CSV16] within the plain UC framework. The resulting treatment is clearer, simpler, and more general. For instance, in our treatment, the Generalized Functionality Composition theorem from [CSV16] turns out to be a direct implication of the standard UC composition theorem.

The other setting is that of composable analysis of blockchains, where assuming global subroutines is essential and permeates all the works in the literature. In a nutshell, in [BMTZ17], a generic ledger was described which, as proved there, is GUC-emulated by (a GUC version of) the Bitcoin backbone protocol [GKL15] in the presence of a global clock functionality used to allow the parties to remain synchronized. This ledger was, in turn, used within another protocol, also having access to the global clock, in order to implement a cryptocurrency-style ledger, which, for example, prevents double spending. [BMTZ17] then argues that using the GUC composition theorem one can replace, in the latter construction, the generic ledger by the backbone protocol. As we demonstrate here, such a generic replacement faces several issues due to inaccuracies in GUC. Instead, we show how to apply our theorem to directly derive the above statement in the UC framework.

Composition with Global Subroutines in Other General Frameworks. Several other general frameworks for defining security of protocols use a static machine model akin to the restricted variant of the UC model described above, where machines communicate only via connections (“ports”) that are fixed ahead of time, and the only way to compose systems is by way of connecting them using a pre-defined set of ports. (Examples include the reactive simulatability of [PW00, BPW07], the IITM framework of Küsters and Thuengertal [KMT20], the abstract cryptography of Maurer and Renner [MR11], the iUC framework of Camenisch et al. [CKKR19].) In these frameworks, the single-instance global-state composition theorem immediately follows from plain secure composition, in very much the same way as the single-instance UCGS theorem follows immediately from the plain UC theorem in the restricted UC model (see Fig. 1).

However, these frameworks do not provide mechanisms for modular analysis of systems where the de-composition of the system to individual modules is determined dynamically during the course of the computation. In particular, composition with global state in these frameworks does not address this important case either. In contrast, as described above, this fully dynamic, multi-instance case is the focus of this work. So far, this case has been addressed only in the GUC and EUC frameworks, as well as in the work of Hofheinz and Shoup [HS16] which proposes an extension of their model to accommodate certain specific ideal functionalities as distinguished machines.

We note that the IITM framework of Küsters and Thuengertal [KMT20] (as well as the recent iUC model [CKKR19] that builds on top of the IITM framework) does contain an additional construct that allows machines to interact in a somewhat dynamically determined way: While each machine has a fixed set of other machines that it can interact with, and protocols are defined as fixed sets of machines that have globally consistent “communication sets”, the framework additionally allows unboundedly many instances of each machine, where all instances have the same identity, code, and “communication set”. Furthermore, if the communication sets of machines $$M,M'$$ allows them to communicate, then each instance of M can communicate with each instance of $$M'$$. Indeed, this additional feature enables the IITM framework to express systems where the communication is arbitrarily dynamic.

However, this extra feature appears to fall short of enabling fully modular analysis of such dynamic systems. Indeed, the IITM framework still can only compose systems along the static, a-priori fixed boundaries of machine ports. This means that systems that include multiple instances of some protocol, where the boundaries of the individual instances are dynamically determined, cannot be analyzed in a modular way—rather, the framework only allows for direct analysis of all protocol instances at once, en bloc. This of course holds even in the presence of global subroutines. Example of such systems include secure pairwise communication systems where the communicating parties are determined dynamically, block-chain applications where different quorums of participants join to make decisions at different times, etc. See e.g.. [BCL+11, CSV16, GHM+17].

In contrast, the goal of this work is to allow de-composing such systems to individual instances, deducing the security of the overall composite system from the security of an individual instance—and carrying this through even when many (or all) instances use the same global subroutines (see Fig. 2).

A related work by Camenisch et al. [CDT19] introduces a new UC variant that they call multi-protocol UC (MUC) and that allows the environment to instantiate multiple challenge protocols that can interact with each other. It is an interesting future research direction to formulate this more general type of UC execution following the approach taken in this work, i.e., to model it following standard UC and making black-box use of the UC composition theorem to derive a composition theorem for this type of protocol.

2 Formulating and Proving the UCGS Theorem

In this section, we formulate and prove the main result of this work. In Sect. 2.1 we present the transformation that takes protocols $$\pi $$ and $$\gamma $$ and constructs a single, transparent encapsulation protocol $$\mathsf {M}[\pi ,\gamma ]$$ that behaves like a single instance of $$\pi $$ along with one (or more) instances of a “global subroutine protocol” $$\gamma $$. We formulate UC emulation with Global Subroutines in Sect. 2.2, state the Universal Composition theorem with Global Subroutines composition in Sect. 2.3 and conclude with remarks in Sect. 2.4. We also provide a proof sketch. See [BCH+20] for the full proof.

2.1 Treating Multiple Protocols as a Single Protocol

We start by defining the transformation that takes two protocols $$\pi $$ and $$\gamma $$ and combines them into a single protocol $$\mu = \mathsf {M}[\pi ,\gamma ]$$, such that one instance of $$\mu $$ behaves like one instance of $$\pi $$ and one or more instances of $$\gamma $$, and where the instances of $$\gamma $$ take inputs both from the instance of $$\pi $$ within $$\mu $$, and from outside $$\mu $$. We refer to $$\mu $$ as the management protocol.

The goal of the construction is to ensure that an instance of protocol $$\mu $$ presents the exact same behavior as one instance of $$\pi $$ alongside one (or more) instances of $$\gamma $$, while at the same time making sure that, from the point of view of the basic UC framework, $$\mu $$ remains a subroutine-respecting protocol. This will mean that incoming communication to $$\mu $$ specifies a session ID for $$\mu $$, plus a session identifier for either the instance of $$\pi $$ or an instance of $$\gamma $$. The input is then forwarded internally either to the instance of $$\pi $$ or to the appropriate instance of $$\gamma $$. Outgoing communication is handled similarly. Note that it is important to make sure that the (virtual) instances of $$\pi $$ and $$\gamma $$ receive communication that is formatted exactly as it would be, were it the case that $$\pi $$ and $$\gamma $$ are independent machines. (This is needed so that the behavior of $$\pi $$ and $$\gamma $$ will remain unchanged.) See depiction in Fig. 3.
../images/508076_1_En_1_Chapter/508076_1_En_1_Fig3_HTML.png
Fig. 3.

The three main components of our management protocol $$\mu =\mathsf {M}[\pi ,\gamma ]$$ handling access to $$\pi $$ and $$\gamma $$, both equipped with shells $$\mathsf {sh}[\cdot ] $$. For $$\mathsf {sh}[\pi ] $$, different types of incoming and outgoing messages are indicated in gray.

In order to allow black-box use of the UC composition theorem in the proof of our new composition theorem, we need to make sure that an instance of $$\mu $$ mimics the execution of a single instance of $$\pi $$ (alongside one or more instances of $$\gamma $$). That is, $$\mu $$ must make sure that the various machines of an instance of $$\mu $$ maintain a single, consistent virtual instance of $$\pi $$. To maintain the necessary information about the execution, we allow the management protocol $$\mu $$ to make use of a directory ITI similar to the one used to ensure the subroutine-exposing property. That is, we embed a special ITI called execution graph directory in the operation of the management protocol (and shells) that acts as a central accumulator of knowledge.2

We now detail the execution graph directory for the structured protocol $$\mu $$. The following generic shell mechanism—implemented by an additional, outermost shell of $$\mu $$ and all its subroutines—makes sure that this outermost shell layer maintains information about the induced execution graph as well as additional auxiliary information extracted from the underlying protocol (i.e. the body in the view of this additional shell). Let $$\mathsf {pid}_{\mathrm {egDIR}}$$ be an exclusive identifier, i.e., an identifier that never appears in any execution of the base protocol. Assume the session identifier is $$\mathsf {sid}$$.

  • The ITI with special identifier $$(\mu ,\mathsf {sid}||\mathsf {pid}_{\mathrm {egDIR}})$$ never activates its body and the shell processes three types of requests: first, when activated with input $$(\textsc {register}, aux )$$ from an ITI M, it stores the entry $$(M, aux )$$ in an ordered list (initially empty) unless M is already recorded in the list. Second, when activated with input $$(\textsc {invoke}, M', aux )$$ from an already registered ITI M and ITI $$M'$$ is not yet registered, then record $$(M\rightarrow M')$$. Also, record $$(M', aux )$$ unless $$M'$$ is already registered. The return value to M in both cases is the trivial output $$\mathsf {ok}$$. The party allows any registered ITI M to query the stored list and ignores any message on the backdoor tape.

  • For any other ITI running in this instance, when activated for the first time, the shell sends $$(\textsc {register}, aux )$$ to ITI $$(\mu ,\mathsf {sid}||\mathsf {pid}_{\mathrm {egDIR}})$$ where $$ aux $$ can denote any auxiliary information. (Note that reveal-sender id and forced-write flags are set). When receiving $$\mathsf {ok}$$ it resumes processing its first activation by activating its body (which in structured protocols might be another shell oblivious of the above interaction).

  • For any other ITI running in this instance, when the shell processes an external write request from its body to an ITI M, it sends $$(\textsc {invoke}, M, aux )$$ to ITI $$(\mu ,\mathsf {sid}||\mathsf {pid}_{\mathrm {egDIR}})$$ where $$ aux $$ can denote any auxiliary information, before resuming with processing the external write request.

By exclusivity of $$\mathsf {pid}_{\mathrm {egDIR}}$$, the shell operates in an oblivious fashion from the point of view of the body. Since the shell only talks to $$\mathsf {pid}_{\mathrm {egDIR}}$$, this in turn is even oblivious to the environment and the adversary.

In fact, this is not entirely obvious: while no interaction via the backdoor tape indeed means that the adversary can neither corrupt nor extract information from the directory, another corrupted ITI in the system might get information from $$\mathsf {pid}_{\mathrm {egDIR}}$$ via a normal query and give the result to the adversary. This, however, is not possible: in UC, model-related instructions are organized in shell layers, where each shell is unaware of the outer shells, and treats the inner shells as part of the body. Now, the shell layer describing the model-related instructions to communicate with directories is outside of the shell implementing the corruption layer and therefore, the corruption layer is unaware of the directory. For more details, see [Can20, Section 5.1]. We note that this observation is already crucial for the standard UC composition theorem and not novel for our work, because corruptions must not invalidate the subroutine-exposing property of a protocol and hence corruptions should not interfere with the subroutine-exposing shell (or the shell introduced by the UC operator).

To conclude, the above mechanism is used by $$\mathsf {M}[\pi ,\gamma ]$$ and its subsidiaries $$\mathsf {sh}[\cdot ] $$ in the following way: first, whenever a new machine with code $$\mathsf {M}[\cdot ]$$ is about to spawn an instance of $$\pi $$, it registers with the directory and defines as auxiliary input the extended identity of the instance of $$\pi $$ it is going to spawn (and can also halt if it sees that another session already started). Second, the machines running code $$\mathsf {sh}[\cdot ] $$ use the $$\textsc {invoke} $$ calls and put as auxiliary input the information $$\mathsf {eid}_\mathrm {src} \rightarrow \mathsf {eid}_\mathrm {dest} $$ of the virtual ITIs of $$\mathsf {sh}[\cdot ] $$ to additionally store the invocation graph of the main instance of $$\pi $$ which in particular allows to infer what the (virtual) main instance of $$\pi $$ is (see below for why this is important). In particular, all ITIs in the extended session of $$\mathsf {M}[\pi ,\gamma ]$$ use the same execution graph directory ITI. To see that we get all properties we need from this, we refer to Proposition 1.

We now give a formal definition of $$\mathsf {M}[\pi ,\gamma ]$$. The construction uses the body and shell formalism from [Can20].

The Management Protocol. In a nutshell, $$\mathsf {M}[\pi ,\gamma ]$$ is a standard UC protocol that works as follows:

  • $$\mathsf {M}[\pi ,\gamma ]$$ exposes its subroutine structure to a directory ITI (which the environment can access) and its invocation graph to an additional execution graph directory ITI as discussed above to ensure that $$\mathsf {M}[\pi ,\gamma ]$$ is subroutine respecting.

  • $$\mathsf {M}[\pi ,\gamma ]$$ can be invoked with an arbitrary session identifier. It allows the environment to invoke exactly one (top-level) instance of $$\pi $$ with a freely chosen session identifier (note that addressing this “challenge protocol” is done in an abstract manner by using an identifier MAIN). Additionally, arbitrarily many instances of $$\gamma $$ (again with arbitrary session identifiers) can be invoked (again the addressing is done in an abstract fashion using identifier GLOBAL).

  • When an ITI running $$\mathsf {M}[\pi ,\gamma ]$$, say with party ID $$\mathsf {pid}$$, provides input to $$\pi $$ in session s, then it wraps this input and invokes the ITI with code $$\mathsf {sh}[\pi ] $$, party id $$\mathsf {pid}$$, and a session ID that encodes s. This ITI unwraps the received content and provides it to the main party $$\mathsf {pid}$$ of $$\pi $$ in session s. A similar mechanism happens between any two machines to ensure that this instance of $$\pi $$ is oblivious of this overlay.

  • The machines running $$\mathsf {sh}[\pi ] $$ (resp. $$\mathsf {sh}[\gamma ] $$) detect, using the execution graph directory, when a “main party of $$\pi $$ (resp. $$\gamma $$)” provides subroutine output to an external party, and can then provide this output to the correct main party $$\mathsf {M}[\pi ,\gamma ]$$ which delivers it to the environment. Note that when $$\mathsf {M}[\pi ,\gamma ]$$ delivers such outputs to the environment, it only reveals the party ID and session ID, and whether the source was the global subroutine (using identifier GLOBAL) or the single invoked instance (using identifier MAIN). Recall that the UC control function plays a similar role. We note in passing that $$\mathsf {M}[\pi ,\gamma ]$$ can ensure that at most one session of $$\pi $$ is invoked by the concept of the execution graph directory and block any attempt to create a new session of $$\pi $$ if one exists already.

  • $$\mathsf {M}[\pi ,\gamma ]$$ refuses to communicate with the adversary, i.e., it does not communicate over the backdoor tape and is hence also incorruptible.

In order to map this to a program, we quickly recall the message passing mechanism in UC. UC uses the external-write mechanism via which a machine can instruct the control function to invoke a machine with a given input on one of three tapes. Messages are either written on the input tape (e.g., when a party calls a subsidiary), or on the subroutine-output tape (e.g., when a subsidiary returns an output to a caller), or on the backdoor tape (which only models the interaction with the adversary). Therefore, our transformation has to take care to route all the messages of the “wrapped” instance of $$\pi $$ to the correct machines by taking care of inputs, subroutine outputs, and backdoor messages.

Code of Transformation. The formal description of the management protocol $$\mathsf {M}[\pi ,\gamma ]$$, which is parameterized by two ITMs $$\pi $$ and $$\gamma $$, as well as the code of the associated shell of the transformation, denoted $$\mathsf {sh}[\mathsf {code}] $$ that takes as parameters the ITM $$\mathsf {code}$$ and is a structured protocol that runs $$\mathsf {code}$$ as its body, are provided in Appendix A.

Runtime Considerations as a Standard UC Protocol. The protocols generated by $$\mathsf {M}[\cdot ]$$ are standard UC protocols executed by an environment $$\mathcal {Z} $$. The run-time of $$\mathsf {M}[\cdot ]$$ and $$\mathsf {sh} [\cdot ]$$ deserves further discussion. Recall that in a parameterized system, each ITI only starts executing after receiving import at least k—where k is the security parameter. That means when $$\mathsf {M}[\cdot ]$$ is first invoked it requires import k to before executing, the execution graph directory requires additional import k, and the sub-protocol $$\mathsf {sh} [\pi ]$$ or $$\mathsf {sh} [\gamma ]$$ to which the message is directed also requires import k before executing. We define $$\mathsf {M}[\cdot ]$$ such that it begins executing only after receiving import at least 3k; this ensures that the initial operation has sufficient import to complete. The further operations performed by $$\mathsf {M}[\cdot ]$$ and the shell $$\mathsf {sh} $$ of $$\pi $$ and $$\gamma $$ are only administrative such as copying and routing messages between ITIs, which means that they can be accounted for by slightly increasing the involved polynomials.

An Alternative Management Protocol. We note that defining $$\mathsf {M}[\pi ,\gamma ]$$ so that the main parties of an instance of $$\mathsf {M}[\pi ,\gamma ]$$ consist of ITIs that run exclusively shell code, and where the ITIs that have body $$\pi $$ or $$\gamma $$ are subroutines of these main parties of $$\mathsf {M}[\pi ,\gamma ]$$, is a design choice that was made mainly for clarity of exposition and to clearly delineate the various parts of the management protocol. Alternatively, one can define a different management protocol, $$\mathsf {M}[\pi ,\gamma ]'$$, where the code of the main ITIs of $$\mathsf {M}[\pi ,\gamma ]$$ becomes part of the shell code of the ITIs whose body runs either $$\pi $$ or $$\gamma $$. That is, the main parties of an instance of $$\mathsf {M}[\pi ,\gamma ]'$$ will be the union of the main parties of the relevant top-level instance of $$\pi $$, along with the main parties of the relevant top-level instances of $$\gamma $$. One advantage of this formalism is that there are no additional management-only ITIs, and so the runtime issues mentioned in the previous paragraph do not come up. In addition, we believe that the restriction to regular setups can be relaxed. Additional details are provided in [BCH+20].

2.2 UC Emulation with Global Subroutines

We now define a variant of UC emulation that intends to capture, within the plain UC model, the notion of EUC-emulation from [CDPW07]. Namely, we say what it means for a protocol $$\pi $$ to UC-emulate another protocol $$\phi $$, in the case where either $$\pi $$ or $$\phi $$ or both are using another protocol $$\gamma $$ as subroutine, where $$\gamma $$ can be accessed as subroutine of other protocols, i.e., is “global” or “shared”.

Definition 1

(UC emulation with global subroutines). Let $$\pi $$, $$\phi $$ and $$\gamma $$ be protocols. We say that $$\pi $$ $$\xi $$-UC-emulates $$\phi $$ in the presence of $$\gamma $$ if protocol $$\mathsf {M}[\pi ,\gamma ]$$ $$\xi $$-UC-emulates protocol $$\mathsf {M}[\phi ,\gamma ]$$.

Note that in the above, $$\xi $$ can be any identity bound as of standard UC. Recall that it is a tool to get more fine-grained security statements and technically restricts the environment to interact with the protocol instances $$\pi $$ and $$\gamma $$ in a certain way.

Our definition of UC-emulation in the presence of a global subroutine is very general, and we need further terminology in preparation for the conditions under which the composition theorem applies. Consider the case where we want to analyze security of multiple instances of a protocol $$\pi $$ which individually are subroutine respecting except that they all call a global subroutine $$\gamma $$. In the terminology of [CDPW07], such protocols are called $$\gamma $$-subroutine respecting. We generalize their definition and allow for more than one instance of $$\gamma $$.

Definition 2
($$\gamma $$-subroutine respecting). A protocol $$\pi $$ is called $$\gamma $$-subroutine respecting if the four conditions of the standard subroutine respecting property required from any (sub-)party of some instance of $$\pi $$ are relaxed as follows:

  • the conditions do not apply to those sub-parties of instance s that also belong to some extended session $$s'$$ of protocol $$\gamma $$;

  • (sub-)parties of s may pass input to machines that belong to some extended session $$s'$$ of protocol $$\gamma $$, even if those machines are not yet part of the extended instance of s.

While the definition above allows $$\pi $$ to violate subroutine respecting through subroutines with a code that is also used by $$\gamma $$, we are only interested in protocols $$\pi $$ where subsidiaries only communicate with outside protocols if they belong to the subroutine $$\gamma $$. To this end, we will only consider $$\gamma $$-subroutine-respecting protocols $$\pi $$ where $$\gamma $$ is itself subroutine respecting.

For our composition theorem to hold, we must impose a light technical condition on the shared subroutine. The condition states that (a) a shared subroutine does not spawn new ITIs by providing subroutine output to them, and (b) the shared subroutine may not invoke the outside protocol as a subroutine. On a high level, this prevents that the shared subroutine itself spawns new higher-level sessions. On a technical level, the composition theorem relies on a hybrid argument that would not work if the shared subroutine spawns, for example, new sessions for which it is not decidable in a dynamic fashion whether or not they actually belong to the main instance of the protocol under consideration. To our knowledge, all global setups used in the literature satisfy these restrictions. For example, a global CRS does not output the reference string to parties who never asked for it, a global ledger requires parties to register before participating in the protocol, and a global clock only tells the time on demand. An example of a hypothetical functionality that violates this condition is a global channel functionality that outputs a message to a receiver whose extended identity can be freely chosen by the sender.

Definition 3

(Regular setup). Let $$\phi ,\gamma $$ be protocols. We say that $$\gamma $$ is a $$\phi $$-regular setup if, in any execution, the main parties of an instance of $$\gamma $$ do not invoke a new ITI of $$\phi $$ via a message destined for the subroutine output tape, and do not have an ITI with code $$\phi $$ as subsidiary.

As will become clear in Proposition 1, when considering a protocol $$\phi $$ that is $$\gamma $$-subroutine respecting, where $$\gamma $$ itself is $$\phi $$-regular and subroutine respecting, then we naturally have a clean interaction between $$\phi $$ and “a global subroutine” $$\gamma $$ without any unexpected artifacts. For example, $$\gamma $$ does not initiate new ITIs with code $$\phi $$, neither as new protocol sessions “outside of $$\gamma $$” nor as proper subroutines of $$\gamma $$ itself.

We next state the useful proposition that our transformation is by default subroutine respecting and preserves the behavior of the involved protocols in the following sense: Let $$\pi , \gamma $$ be as before, and let $$\alpha $$ be a protocol that invokes at most one session of $$\pi $$. Let $$\widehat{\alpha }$$ be the protocol that executes $$\alpha $$ as a virtual ITI within a shell. Let $$\mathsf {sid}_\mathrm {M}$$ be an otherwise unused SID.

  • When $$\alpha $$ provides input m to ITI $$\mathsf {eid}_\mathrm {dest} $$ with code $$\mathsf {code}\in \{\pi ,\gamma \}$$, then $$\widehat{\alpha }$$ instead provides input $$((m, \mathsf {eid}_\mathrm {src}), \mathsf {eid}_\mathrm {dest} ')$$ to $$\mathsf {M}[\pi ,\gamma ]$$ with SID $$\mathsf {sid}_\mathrm {M}$$, where $$\mathsf {eid}_\mathrm {src} $$ is the extended identity of the virtual instance of $$\alpha $$ and $$\mathsf {eid}_\mathrm {dest} '$$ equals $$\mathsf {eid}_\mathrm {dest} $$ except that its code-field $$\mathsf {code}'$$ is set to MAIN if $$\mathsf {code}= \pi $$ and to GLOBAL if $$\mathsf {code}=\gamma $$ (and results in the same subroutine being invoked as $$\alpha $$ does).

  • When $$\widehat{\alpha }$$ obtains subroutine output $$((m, \mathsf {eid}_\mathrm {src}), \mathsf {eid}_\mathrm {dest})$$ from $$\mathsf {M}[\pi ,\gamma ]$$ with SID $$\mathsf {sid}_\mathrm {M}$$, where $$\mathsf {eid}_\mathrm {dest} $$ is the extended identity of the virtual instance of $$\alpha $$, then $$\widehat{\alpha }$$ emulates subroutine output m from $$\mathsf {eid}_\mathrm {src} $$ to $$\alpha $$, overwriting code MAIN of $$\mathsf {eid}_\mathrm {src} $$ with $$\pi $$ and code GLOBAL with $$\gamma $$.

Proposition 1

($$\mathsf {M}[\pi ,\gamma ]$$ is subroutine respecting and preserves behavior). Let $$\gamma $$ be subroutine respecting and $$\pi $$ be $$\gamma $$-subroutine respecting. Then the protocol $$\mathsf {M}[\pi ,\gamma ]$$ is subroutine respecting. In addition, let $$\gamma $$ be $$\pi $$-regular, and let $$\alpha $$ be a protocol that invokes at most one subroutine with code $$\pi $$. Denote by $$\widehat{\alpha }$$ the transformed protocol described above. Then the transcript established by the set of virtual ITIs in an execution of some environment with $$\widehat{\alpha }$$ is identical to the transcript established by the set of ITIs induced by the environment that has the same random tape but interacts with $$\alpha $$.

The proof is deferred to [BCH+20].

2.3 Universal Composition with Global Subroutines

We are now ready to state a composition theorem that lets us replace protocol instances in the presence of a global setup. See Fig. 4 for a graphical depiction.
../images/508076_1_En_1_Chapter/508076_1_En_1_Fig4_HTML.png
Fig. 4.

A graphical depiction of our composition theorem in the presence of global setups. Top: $$\pi $$ UC-emulates $$\phi $$ (Definition 1). Bottom: Replacement of $$\phi $$ by $$\pi $$ in some context protocol $$\rho $$. See Theorem 1 for the assumptions made on $$\rho ,\pi $$ and $$\gamma $$ for replacement to go through. Empty boxes indicate subroutines of $$\rho $$ that are not $$\pi $$ or $$\phi $$.

Theorem 1

(Universal Composition with Global Subroutines – UCGS Theorem). Let $$\rho ,\phi ,\pi ,\gamma $$ be subroutine-exposing protocols, where $$\gamma $$ is a $$\phi $$-regular setup and subroutine respecting, $$\phi ,\pi $$ are $$\gamma $$-subroutine respecting and $$\rho $$ is $$(\pi ,\phi ,\xi )$$-compliant and $$(\pi ,\mathsf {M}[\mathsf {code},\gamma ],\xi )$$-compliant for $$\mathsf {code}\in \{\phi ,\pi \}$$. Assume $$\pi $$ $$\xi $$-UC-emulates $$\phi $$ in the presence of $$\gamma $$, then $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$.

In line with the run-time discussion for $$\mathsf {M}[\cdot ]$$, protocol $$\rho $$ only starts executing after receiving import at least 4k. This ensures that, during the execution, the modified version of $$\rho $$ (which we refer to as $$\vartheta $$ in the proof) has a sufficient run-time budget to accommodate the creation of the additional ITI $$\mathsf {M}[\mathsf {code},\gamma ]$$, its execution graph directory, as well as an additional directory introduced by the proof technique in this theorem.

Proof

(outline). In the spirit of our overall approach, we aim at applying the UC composition theorem instead of reproving composition from scratch. Thus, we choose the following high level structure of the proof. We modify each invocation of $$\phi $$ within $$\rho $$ separately. For each $$i=1,\dots ,n$$, we first rewrite $$\rho $$ such that the management protocol $$\mathsf {M}[\phi ,\gamma ]$$ is invoked instead of the i-th $$\phi $$. Then, we replace $$\phi $$ with $$\pi $$ within this instance of the management protocol. This is done by invoking the UC composition theorem. Afterwards, we remove the management protocol instance again and let $$\rho $$ instead call $$\pi $$ directly. All modifications are oblivious from the perspective of the environment. The full proof can be found in [BCH+20].    $$\square $$

We point out that our composition proof makes it explicit that no changes to the concrete interaction between $$\phi $$ (resp. $$\pi $$) and the instances of the global subroutine $$\gamma $$ are needed. This is important point to consider, since often all instances of $$\phi $$ (resp.$$\pi $$) within $$\rho $$ would share the same instance (or a fixed number of instances) of $$\gamma $$ and hence our theorem shows that this behavior is preserved. Such specific cases (where a bounded number of instances of $$\gamma $$ can be assumed to exist) follow as a special case of our treatment.

2.4 On Existing Global UC Statements and Proofs

In general, statements found in the literature work in the externalized UC (EUC) subspace of GUC. Although we argue in [BCH+20] that EUC as a framework has some subtle issues, most known protocols do look fine in a meaningful context (which should be made explicit). First, most global setups in the literature are easily seen to be regular, i.e., only provide output to the requesting ITI (examples include a clock, random oracle, ledger functionality). Next, proofs typically assume a sort of domain separation between claimed identities by the environment and real ITIs in the system. (Note that this is not given by the model: even if the environment cannot claim external identities in the same session as the test session, the test session does not have to exist when first accessing the global setup.) In UC 2020 [Can20], one can define $$\xi $$ as a condition on allowed identities in the system. Two typical restrictions are found in the literature such as in [BMTZ17]:
  1. (a)

    $$\xi $$ is satisfied if (i) any $$\mathsf {eid}$$ of an ITI in the system is not declared by the environment as an external source $$\mathsf {eid}$$ in a request to $$\gamma $$. This is typically a minimal requirement, as otherwise, whatever the global setup provides to a protocol, this information could be first claimed by the environment (for the entire test session) even before spawning the test session. This is problematic unless we have very simple setups such as a common-reference string or a plain global random oracle [BGK+18].

     
  2. (b)

    As a further restriction, one could enforce that $$\gamma $$ provides per session guarantees: $$\xi $$ is satisfied if whenever (additionally to above) $$\mathsf {eid}=(\mu ,\mathsf {sid}||\mathsf {pid})$$ and $$\mathsf {eid}'=(\mu ',\mathsf {sid}||\mathsf {pid}')$$ are the source extended identities in an input to $$\gamma $$, then $$\mu = \mu '$$ has to hold. This technically does not allow any other instance to access the shared information, but still the information is formally accessible by the environment claiming an external identity of this session. This model is useful when certain elements of the setup need to be programmed by a simulator, while keeping the overall model of execution close to standard UC.

     

If proofs conducted in EUC have the above restrictions assumed when proving indistinguishability of the simulation, then it is conceivable that these proofs are transferable into our new model to satisfy precondition of Theorem 1 and thus composition is again established. We discuss such “EUC statements” in the next section. In particular, Sect. 3.2 recovers an EUC example in detail, where we also show how our model can capture various forms of “shared subroutines” ranging from subroutines fully accessible by the environment to subroutines shared only by the challenge protocol (which captures joint-state UC (JUC)).

3 Applications of the UCGS Theorem

We provide two examples to showcase how to prove emulation statements in the UC model in the presence of global subroutines and to verify that the preconditions of the UCGS Theorem are satisfied. The first example is global public-key infrastructure (specifically, adapting the treatment of [CSV16]). The second example is a global clock (adapting the treatment of [BMTZ17]).

These examples bring forth two additional technical aspects of universal composition with global subroutines within the UC framework: The first has to do with the mechanics of having one ideal functionality call another ideal functionality as a subroutine, and the second has to do with the need to find a judicious way to define the external-identities predicate $$\xi $$ for the management protocol so as to make the best use of the UCGS theorem. (Indeed, these aspects of UC with global subroutines have been lacking in the treatment of [CDPW07].)

Section 3.1 introduces the formalism for having an ideal functionality call another ideal functionality as subroutine. Section 3.2 presents the application to modeling global public-key infrastructure. Section 3.3 presents the application to modeling global clock in the context of blockchains.

3.1 Interaction Between Ideal Functionality and Shared Subroutine

The UCGS theorem essentially state that if protocol $$\pi $$ UC-emulates protocol $$\phi $$ in the presence of $$\gamma $$, and both $$\pi $$ and $$\phi $$ are $$\gamma $$-subroutine respecting, then $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$ for any $$\rho $$. A natural use-case of the theorem is when the emulated protocol, $$\phi $$, is an ideal protocol for some ideal functionality $$\mathcal {F}$$, and $$\gamma $$ is an ideal protocol for some ideal functionality $${\mathcal {G}}$$. This means that to make meaningful use of the theorem, $$\mathcal {F}$$ should make subroutine calls to $$\gamma $$, which in this case means that $$\mathcal {F}$$ should call dummy parties for $${\mathcal {G}}$$.

A simplistic way to do that would be to simply have $$\mathcal {F}$$ directly call (and thus create) dummy parties for $${\mathcal {G}}$$. However, in this case, by the definition of dummy parties as per the UC framework [Can20], the PID of the created dummy party will be the identity of $$\mathcal {F}$$. This may be overly restrictive, since the emulating protocol, $$\pi $$ might have other ITIs call $${\mathcal {G}}$$. So, instead, we define a mechanism whereby $$\mathcal {F}$$ does not directly call a dummy party for $${\mathcal {G}}$$. Instead, $$\mathcal {F}$$ creates a new “intermediate dummy party,” which serves as a relay of inputs and outputs between $$\mathcal {F}$$ and the dummy party of $${\mathcal {G}}$$. The identity (specifically the PID) of the intermediate dummy party is determined (by $$\mathcal {F}$$) so as to enable realization of $$\phi $$ by protocols $$\pi $$ where the PIDs of the parties that use $${\mathcal {G}}$$ are meaningful for the overall security. (This mechanism can be viewed as a way to make rigorous informal statements such as “provide input x to $${\mathcal {G}}$$ on behalf of [sender] S” [CSV16].) Details follow.

Definition 4

(Intermediary dummy party). Let $$\mathcal {F}$$ be an ideal functionality and $$\gamma $$ some protocol. We define the operation of an intermediary dummy party with code $$\textsc {IM}_{\mathcal {F},\gamma }$$ as below. Let (p, s) be the party and session id indicated on the identity tape, and let $$\mathsf {CIM}$$ (code of intermediary) be an exclusive syntactic delimiter ending the description of the code $$\textsc {IM}_{\mathcal {F},\gamma }$$.

  • When activated with input $$(\textsc {call}, (s',p'), v)$$ from an ITI with code $$\mathcal {F}$$ and sid s: the party only acts if the content of the identity tape matches $$(\cdot ||\mathsf {CIM},\cdot ||\cdot )$$ and the reveal-sender-id flag is set. Then, provide input v to the ITI $$\mathsf {eid}_t := (\gamma , s'||p')$$ (with reveal-sender identity and forced-write flags set).

  • Upon receiving a value $$v'$$ on the subroutine output from an ITI with identity $$\mathsf {eid}= (\gamma , s'||p')$$ (for some $$s',p'$$): the party only acts if the content of the identity tape matches $$(\cdot ||\mathsf {CIM},\cdot ||\cdot )$$ and the reveal-sender-id flag is set. Then, provide subroutine output $$(\textsc {return}, (s', p'), v')$$ to the ITI with identity $$\mathsf {eid}_t := (\mathcal {F}, s||\bot )$$ (with reveal-sender identity and forced-write flags set).

  • Any other message on any tape that is not matching to some case above is ignored.

A functionality $$\mathcal {F}$$ can now contain general instructions of the form “provide input x on behalf of P in session s to an instance of $$\gamma $$ running in session $$s'$$ and PID $$P'$$” and is understood as the following operation: the ITI running code $$\mathcal {F}$$ in some session $$\mathsf {sid}$$ provides input $$(\textsc {call}, (s',P'), x)$$ to intermediary dummy party with identity (s, P) and code $$\textsc {IM}_{\mathcal {F},\gamma }$$. Now, P (in session s) will appear as the PID of the ITI invoking $$\gamma $$. $$\mathcal {F}$$ can process the answers when obtaining the returned values from the intermediary dummy party on its subroutine output tape.

Often it is clear from the context—and standard for EUC-like statements—that only one session of $$\gamma $$ with a predefined session identifier $$\tilde{\mathsf {sid}}$$ is expected to be running, and that each main party (with PID) P of the challenge session s can participate in the shared process $$\gamma $$ (i.e. by invoking ITI with identity $$(\tilde{s},P)$$ and code $$\gamma $$). In such cases, the statement “output x on behalf of P to $$\gamma $$” by an ideal functionality $$\mathcal {F}$$ in (challenge) session s is understood as providing input $$(\textsc {call}, (\tilde{s}, P), x)$$ to the intermediary dummy party with identity (s, P) (and code $$\textsc {IM}_{\mathcal {F},\gamma }$$) with exactly the desired effect that the ITI with code $$\gamma $$, PID P and sid $$\tilde{\mathsf {sid}}$$ is invoked, and where P in session s appears as the official caller.

Clearly, the intermediary is a modeling tool that no environment should tamper with. Hence, for the sake of clarity, when we speak of UC realization of an ideal functionality interacting with a global subroutine, we mean the following:

Definition 5

(Realization with interaction with shared subroutine). We say that $$\pi $$ UC-realizes $$\mathcal {F}$$ in the presence of $$\gamma $$ w.r.t. $$\xi $$-identity bounded environments, if Definition 1 holds for the particular choice of ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq552_HTML.gif and with respect to the identity bound $$\xi '$$ that equals $$\xi $$ augmented with the restriction that no $$\mathsf {eid}$$ specified by the environment (source or destination) can specify code with delimiter $$\mathsf {CIM}$$.

The intermediary dummy party provides a guaranteed interaction channel and formalizes what was implicitly assumed in prior work when a functionality interacts with, e.g., a global setup such as an certification functionality in the name of a party.

3.2 Example 1: Authentication with Global Certification

Authentication with respect to a global certification functionality (often called PKI) aims at formalizing the fact that if a certified verification key for a digital signature is globally available, then any signature generated with respect to that key can be verified globally, by anyone, even if the signature was generated in the context of a specific protocol. This in particular mean that protocols that employ certified digital signatures might have global “side effects”. For example, if Alice signs a message in a particular session, using a signing key for which there is a globally accessible certificate, then anyone can cross-check that it was Alice who signed the message. In particular, this might mean that Alice can incur further liabilities.

[CSV16] provides a treatment of this situation within the GUC framework of [CDPW07]. We use the UCGS theorem provide an alternative (and arguably simpler) treatment within the plain UC framework.

The Global Certification Functionality. The shared subroutine is ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq557_HTML.gif. Note that the functionality is parameterized by a party identity $$\mathsf {pid}$$. We assume that the functionality is following the standard PID-wise corruption mechanism as specified in [Can20]: this means that the functionality manages corruption messages for party identifiers that are main parties in the execution of ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq559_HTML.gif, and marks those party identifiers as corrupted for which it received a corruption message on the backdoor tape.3
../images/508076_1_En_1_Chapter/508076_1_En_1_Figa_HTML.png

The Protocol. The protocol $$\phi ^{A}_\mathrm {auth}$$ works as follows, where the shared subroutine is ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq601_HTML.gif, where A is part of the code. Note that we use the $$\mathsf {eid}$$ of the caller as the PID of the sender (to prevent that arbitrary machines can send messages in the name of A), and also simply choose the session-id $$\mathsf {sid}_0=A$$ for the shared subroutine. We further assume an unprotected medium to send messages, which as specified in [Can20] can be modeled by simply letting the shell forward sent messages to the adversary (via the backdoor tape) and interpret specific inputs on the backdoor tape as received messages.

  1. (a)

    Upon receiving an input $$(\textsc {Send}, \mathsf {sid}, B, m)$$ from party A4, verify that this machine’s eid is $$(\phi ^{A}_\mathrm {auth},\mathsf {sid}||A)$$; otherwise, ignore the request. Then, set $$\mathsf {sid}_0 = A$$ and $$m' = (m; \mathsf {sid};B)$$, send $$(\textsc {Sign}, m')$$ to $${{\mathcal {G}}^{A}_{\mathrm {cert}}}$$ (i.e., the input is given to the ITI running code $$\gamma $$ in session $$\mathsf {sid}_0$$ with $$\mathsf {pid}=A$$) to obtain the response $$(\textsc {Signature}, \mathsf {sid}_0,m',\sigma )$$, send $$(\mathsf {sid};A;m;\sigma )$$ to ITI $$(\phi ^{A}_\mathrm {auth},\mathsf {sid}||B)$$ (via the unprotected communication medium).

     
  2. (b)

    Upon receiving message $$(\mathsf {sid}';A;m;\sigma )$$ from the unprotected communication medium, this party, denote its eid by $$(\phi ^{A}_\mathrm {auth},\mathsf {sid}||B)$$, sets $$\mathsf {sid}_0 = A$$, sets $$m' = (m;\mathsf {sid};B)$$, sends $$(\textsc {Verify}, \mathsf {sid}_0,m',\sigma )$$ to $${{\mathcal {G}}^{A}_{\mathrm {cert}}}$$ (i.e., the input is given to the ITI running code $$\gamma $$ in session $$\mathsf {sid}_0$$ with $$\mathsf {pid}=B$$), and obtains a response $$(\textsc {Verified}, m', f)$$. If $$f = 1$$ then B outputs $$(\textsc {Sent},\mathsf {sid},A,B,m)$$ (with target eid $$\mathsf {eid}_t = B$$) and halts. Else B halts with no output.

     

We also assume here standard byzantine corruption of protocol ITIs as defined in [Can20]: for a structured protocol, this involves interaction with a special corruption aggregation ITI that aggregates all corruption information (provided by the shell of the protocols). The goal of this is that the environment receives “genuine” information about the corruption sets during the execution. The corruption aggregation is identified by a special PID $$\mathscr {A}$$.

The Realized Functionality. The realized functionality provides authenticated message exchange between a sender A and a chosen receiver. Note that the adversarial ability to obtain legitimate signatures on messages allows to produce a publicly verifiable trail of the message transmission between A and B (which is referred to by the term non-deniable in [CSV16]). As above, we follow the standard PID-wise corruption model for functionalities [Can20].
../images/508076_1_En_1_Chapter/508076_1_En_1_Figb_HTML.png

The Identity Bound on the Environment. In order to show in which contexts the protocol is secure, we have to specify an identity bound. For the result to be broadly applicable, we have to find the least restrictive conditions on the allowed interaction between the environment and the challenge protocol (and $$\gamma $$) such that the realization statement holds.

In our specific case, we can give the following guarantee which basically says that the environment cannot claim the extended identity of the signer: more precisely, we mean that the environment is not allowed to claim source eid $$\mathsf {eid}$$ in requests to $$\pi $$ running in a session s if $$\mathsf {eid}$$ has been already used as the PID to sign a value $$(m,s,\cdot )$$ and PID is not marked as corrupted. Conversely, the environment is not allowed to invoke $$\gamma $$ to sign a value $$(m,s,\cdot )$$ using as PID an extended id $$\mathsf {eid}$$ which has been used before as the caller of $$\pi $$ running in session s and which is not marked as corrupted. Furthermore, it is not allowed that the environment provides input to the ITI $$(\gamma ,\cdot ||\mathscr {A})$$ (where “not allowed” means that the input provided by the environment is formally rejected if the condition is satisfied by the state of the system at the moment of providing the input. See more details in [Can20]). All other invocations are allowed.

Implications of the Above Identity Bound. Recall that any non-trivial bound $$\xi $$ restricts the class of context protocols $$\rho $$ for which the UCGS theorem applies: Essentially the theorem applies only to those protocols $$\rho $$ which manage to guarantee that the bound $$\xi $$ remains valid for any combination of $$\phi $$ and $$\gamma $$ as subroutines within $$\rho $$, and similarly for any combination of $$\pi $$ and $$\gamma $$ as subroutines of $$\rho ^{\phi \rightarrow \pi }$$. In the above case, this means that authenticity of the sender identity is guaranteed as long as the context protocol $$\rho $$ makes sure that the global certification module $$\gamma $$ only takes signature requests from entities that correctly represent their identity. Since the underlying model guarantees that the caller identity is correctly represented, except for the case of inputs provided by the environment, this means that authenticity is guaranteed as long as $$\rho $$ makes sure that $$\gamma $$ does not take inputs directly from the environment.

We note that the restriction also touches the corruption model in order to ensure PID-wise corruption. We force the environment to obtain the system’s corruption information only through one corruption aggregation machine, which in our case is the functionality (resp. challenge protocol) that provides the entire system’s view to $$\mathcal {Z} $$. Note that this is in accordance with the approach that there is exactly one machine in an execution that provides this information to the environment. We thus have:

Lemma 1

Let I be an extended identity, and let $$\xi _{\bar{I}}$$ be the predicate that allows all extended identities other than I as described above. Protocol $$\phi ^{I}_\mathrm {auth}$$ UC-realizes $$\mathcal {F}^{I}_\mathrm {cert\text {-}auth}$$ in the presence of ../images/508076_1_En_1_Chapter/508076_1_En_1_IEq702_HTML.gif with respect to the identity bound $$\xi _{\bar{I}}$$.

The proof is deferred to [BCH+20].

3.3 Example 2: Composable Blockchains with a Global Clock

Motivation. We next showcase the shared-setups composition theorem by demonstrating how it can be applied to obtain composition (i.e., subroutine replacement) in a context in which global (shared) setups have recently become the norm, namely that of composable blockchains. Concretely, a number of recent works [BGK+18, BGM+18, KKKZ18, BMTZ17] analyze the backbone protocol (intuitively corresponding to the the consensus layer) of mainstream cryptocurrencies, such as Bitcoin and Ouroboros assuming a global (shared) clock functionality which is used for enforcing synchrony.

In a nutshell these works prove that by providing access to a global clock $${\mathcal {G}}_{\mathrm {clock}}$$ (along with some additional local or global setups) the underlying backbone implements a functionality $$\mathcal {F}_{\mathrm {Ledger}}$$ that abstract a transaction ledger with eventual consistency guarantees (more concretely, a ledger enforcing the so-called common-prefix, liveness, and chain quality property, cf. [GKL15, PSS17].

Let us focus on [BMTZ17]. This work proved that inducing a special way (discussed below) in which the global (shared) clock functionality is used—i.e., a special registration/deregistration mechanism—there exists a simulator in the $$\{\mathcal {F}_{\mathrm {Ledger}},{\mathcal {G}}_{\mathrm {clock}} \}$$-hybrid world that emulates the behavior of any adversary attacking the Bitcoin backbone protocol in the $$\{{\mathcal {G}}_{\mathrm {clock}},\mathcal {F}_{\mathrm {RO}},\mathcal {F}_{\mathrm {net}} \}$$-hybrid world, where $$\mathcal {F}_{\mathrm {RO}}$$ and $$\mathcal {F}_{\mathrm {net}}$$ are standard (local to the protocol) UC functionalities. The goal of this modeling is to enable abstracting the internals of the ledger protocol, designing protocols that have access to the ledger functionality (and the global clock), and then using the GUC theorem to argue that any protocol which is proved security assuming access to this local ledger functionality will remain secure when the functionality is replaced by the Bitcoin backbone protocol. Assuming existence of such a composition theorem, [BMTZ17] proceeded in proposing a construction of a cryptocurrency ledger—namely a ledger functionality that also checks signatures of parties—assuming a ledger as above and a signatures functionality. However, as discussed, the GUC modeling does not provide sufficiently detailed treatment of external identities so as to make the above approach go through.

We show how the UCGS Theorem can be used by arguing that the preconditions of Theorem 1 are satisfied for the involved components.

Context Restrictions. First we need to fix the (identity bound) predicate $$\xi $$ used to define the applicable context. Recall, that $$\xi $$ is intended to restrict the set (or rather the sequence) of extended identities that the environment can claim when contacting protocols. Let us first consider what happens if we do not impose any restriction. We argue that any such unrestricted access makes the global clock functionality behave in a way that no longer ensures synchrony.

To this direction let us recall the basic idea behind clock $${\mathcal {G}}_{\mathrm {clock}}$$. For clarity, we show a concrete clock functionality formulated in our model in Fig. 5. The functionality $${\mathcal {G}}_{\mathrm {clock}} $$ stores a monotonically increasing counter $$\tau _\mathsf {sid}$$ (corresponding to the current time or global round) which any party can request by issuing a special $$\textsc {clock-read} $$ command. Furthermore, any honest party can send a message $$\textsc {clock-update} $$ to the clock which records it and once all honest parties have sent such a request while the time was $$\tau _\mathsf {sid}$$, the clock increases its time, i.e., sets $$\tau _\mathsf {sid}:=\tau _\mathsf {sid}+1$$.

The above clock was used as follows to ensure synchrony—i.e., that no party starts its round $$\rho +1$$ before every party has finished round $$\rho $$—which was a property necessary for the security proof in the above blockchain protocols: In each round, as soon as a party has completed all its actions (sent and received all its messages) for the current round, it signals this to the clock by sending a $$\textsc {clock-update} $$ command; from that point on this party keeps asking the clock for the time whenever activated and proceeds to the next round only once it observes that this counter advances. As the latter event requires everyone to signal that they are done with the current round, this gives us the desired synchrony guarantee. Notably, by design of the setup, any $${\mathcal {G}}_{\mathrm {clock}} $$-ideal protocol $$\gamma $$ is trivially regular (according to Definition 3). This is true because the clock has a special registration mechanism which forces it to only talk to ITIs which have already registered with it and therefore never spawns new ITIs as required by that definition.

So what happens to the above, when $$\xi $$ is overly liberal? If the environment is allowed to impersonate the protocol session of a party towards the clock (by issuing an external write request with the source-ID being the session of that party) then the environment is able to make the clock advance without waiting for this party, thus entirely destroys the above round structure. This points to the following natural $$\xi $$: The environment is not able to issue any request to the clock which has source ID the ID of a party that already exists in the system, or to spawn any ITI for which it already claimed an external identity before in an interaction with the clock. This corresponds to item (a) in the last paragraph of Sect. 2.4.5 This requirement is assumed and shown to be sufficient in [BMTZ17] and therefore implies that the environment cannot make the clock ignore existing honest parties playing the protocol, hence the clock will enable the above synchronous rounds structure. In the following we will use this $$\xi $$ to apply Theorem 1; for clarity we denote it as $$\xi _{sync}$$.
../images/508076_1_En_1_Chapter/508076_1_En_1_Fig5_HTML.png
Fig. 5.

A global clock functionality. We remark that due to the clean definition of shared subroutines in our model, the depicted global clock has a simpler structure than the clock in the original version of [BMTZ17]. Still, the clock offers the same functionality towards calling ITIs.

Applying the Composition Theorem. Assume now that we want to prove that in the aforementioned construction of the cryptocurrency ledger from the simpler (backbone) ledger $$\mathcal {F}_{\mathrm {Ledger}}$$ from [BMTZ17] we can replace the simpler ledger $$\mathcal {F}_{\mathrm {Ledger}}$$ by the backbone protocol. This corresponds to proving Theorem 1 for $$\gamma $$ being the $${\mathcal {G}}_{\mathrm {clock}} $$-ideal protocol, $$\pi $$ being the backbone protocol, $$\phi $$ being the $$\mathcal {F}_{\mathrm {Ledger}} $$-ideal protocol, and $$\rho $$ being the construction of the cryptocurrency ledger with access to $$\phi $$. All protocols, $$\pi , \phi ,\rho $$ can access protocol $$\gamma $$. First, by inspection of these protocols, we can verify that $$\rho ,\phi ,\pi ,\gamma $$ are subroutine respecting. Note that although the protocols logic is involved, the subroutine structure is quite simple (i.e., subroutine calls only go to ideal protocols that formalize either local or global setups). In particular, although not directly claimed in the original version of in [BMTZ17], it is possible to convert both $$\phi $$ and $$\pi $$ into subroutine-exposing protocols by applying the exposing mechanism (by equipping the protocols with the respective subroutine-exposing shell). Finally, both $$\pi $$ and $$\phi $$ are by design subroutine respecting except with calls to $$\gamma $$ (note that this is due to the fact that a similar concept exists in EUC). Finally, restricting the environment via $$\xi _{sync}$$ ensures that the use of $$\gamma $$ (i.e., the clock) will induce the desired synchronous structure specified for the simulation proof from [BMTZ17]. Given all of this, the UC-realization proof of [BMTZ17] can be translated to this model (the overhead is identical to the overhead in the previous example) to conclude that $$\pi $$ UC-emulate $$\phi $$ in the presence of $$\gamma $$ when the environment is $$\xi _{sync}$$-identity-bounded. Thus we can apply Theorem 1 to prove that $$\rho ^{\phi \rightarrow \pi }$$ UC-emulates $$\rho $$ whenever the context protocol calls the subroutine (to be replaced) in the legal way as defined by $$\xi _{sync}$$ and obtain the desired statement.

Acknowledgments

We thank the anonymous reviewers of Eurocrypt and TCC 2020 for their corrections and suggestions to improve this work.