CHAPTER XXVIII
The Climax of Greek Science
I. EUCLID AND APOLLONIUS
THE fifth century saw the zenith of Greek literature, the fourth the flowering of philosophy, the third the culmination of science. The kings proved more tolerant and helpful to research than the democracies. Alexander sent to the Greek cities of the Asiatic coast camel loads of Babylonian astronomical tablets, most of which were soon translated into Greek; the Ptolemies built the Museum for advanced studies, and gathered the science as well as the literature of the Mediterranean cultures into the great Library; Apollonius dedicated his Conies to Attalus I, and under the protection of Hieron II Archimedes drew his circles and reckoned the sand. The fading of frontiers and the establishment of a common language, the fluid interchange of books and ideas, the exhaustion of metaphysics and the weakening of the old theology, the rise of a secularly minded commercial class in Alexandria, Rhodes, Antioch, Pergamum, and Syracuse, the multiplication of schools, universities, observatories, and libraries, combined with wealth, industry, and royal patronage to free science from philosophy, and to encourage it in its work of enlightening, enriching, and endangering the world.
About the opening of the third century—perhaps long before it—the tools of the Greek mathematician were sharpened by the development of a simpler notation. The first nine letters of the alphabet were used for the digits, the next letter for 10, the next nine for 20, 30, etc., the next for 100, the next for 200, 300, and so forth. Fractions and ordinals were expressed by an acute accent after the letter; so, according to the context, l’ stood for one tenth or tenth; and a small l under a letter indicated the corresponding thousand. This arithmetical shorthand provided a convenient system of computation; some extant Greek papyri crowd complicated calculations, ranging from fractions to millions, into less space than similar reckonings would require in our own numerical notation.*
Nevertheless the greatest victories of Hellenistic science were in geometry. To this period belongs Euclid, whose name would for two thousand years provide geometry with a synonym. All that we know of his life is that he opened a school at Alexandria, and that his students excelled all others in their field; that he cared nothing about money, and when a pupil asked, “What shall I profit from learning geometry?” bade a slave give him an obol, “since he must make a gain out of what he learns”;1 that he was a man of great modesty and kindliness; and that when, about 300, he wrote his famous Elements, it never occurred to him to credit the various propositions to their discoverers, because he made no pretense at doing more than to bring together in logical order the geometrical knowledge of the Greeks.* He began, without preface or apology, with simple definitions, then postulates or necessary assumptions, then “common notions” or axioms. Following Plato’s injunctions, he confined himself to such figures and proofs as needed no other instruments than ruler and compasses. He adopted and perfected a method of progressive exposition and demonstration already familiar to his predecessors: proposition, diagrammatic illustration, proof, and conclusion. Despite minor flaws the total result was a mathematical architecture that rivaled the Parthenon as a symbol of the Greek mind. Actually it outlived the Parthenon as an integral form; for until our own century the Elements of Euclid constituted the accepted textbook of geometry in nearly every European university. One must go to the Bible to find a rival for it in enduring influence.
A lost work of Euclid, the Conies, summarized the studies of Menaechmus, Aristaeus, and others on the geometry of the cone. Apollonius of Perga, after years of study in Euclid’s school, took this treatise as the starting point of his own Conies, and explored in eight “books” and 387 propositions the properties of the curves generated by the intersection of a cone by a plane. To three of these curves (the fourth being the circle) he gave their lasting names—parabola, ellipse, and hyperbola. His discoveries made possible the theory of projectiles, and substantially advanced mechanics, navigation, and astronomy. His exposition was laborious and verbose, but his method was completely scientific; his work was as definitive as Euclid’s, and its seven extant books are to this day the most original classic in the literature of geometry.
II. ARCHIMEDES
The greatest of ancient scientists was born at Syracuse about 287 B.C., son of the astronomer Pheidias, and apparently cousin to Hieron II, the most enlightened ruler of his time. Like many other Hellenistic Greeks who were interested in science and could afford the expense, Archimedes went to Alexandria; there he studied under the successors of Euclid, and derived an inspiration for mathematics that gave him two boons—an absorbed life and a sudden death. Returning to Syracuse, he devoted himself monastically to every branch of mathematical science. Often, like Newton, he neglected food and drink, or the care of his body, in order to pursue the consequences of a new theorem, or to draw figures in the oil on his body, the ashes on the hearth, or the sand with which Greek geometers were wont to strew their floors.2 He was not without humor: in what he considered his best book, The Sphere and the Cylinder, he deliberately inserted false propositions (so we are assured), partly to play a joke upon the friends to whom he sent the manuscript, partly to ensnare poachers who liked to appropriate other men’s thoughts.3 Sometimes he amused himself with puzzles that brought him to the verge of inventing algebra, like the famous Cattle Problem that so beguiled Lessing;4 sometimes he made strange mechanisms to study the principles on which they operated. But his perennial interest and delight lay in pure science conceived as a key to the understanding of the universe rather than as a tool of practical construction or expanding wealth. He wrote not for pupils but for professional scholars, communicating to them in pithy monographs the abstruse conclusions of his research. All later antiquity was fascinated by the originality, depth, and clarity of these treatises. “It is not possible,” said Plutarch, three centuries later, “to find in all geometry more difficult and intricate questions, or more simple and lucid explanations. Some ascribe this to his natural genius; others think that these easy and unlabored pages were the result of incredible effort and toil.’5
Ten of Archimedes’ works survive, after many adventures in Europe and Arabia. (1) The Method explains to Eratosthenes, with whom he had formed a friendship in Alexandria, how mechanical experiments can extend geometrical knowledge. This essay ended the ruler-and-compass reign of Plato and opened the door to experimental methods; even so it reveals the different mood of ancient and modern science: the one tolerated practice for the sake of theoretical understanding, the other tolerates theory for the sake of possible practical results. (2) A Collection of Lemmas discusses fifteen “choices,” or alternative hypotheses, in plane geometry. (3) The Measurement of a Circle arrives at a value between 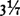 and
and 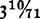 for π—the ratio of the circumference to the diameter of a circle—and “squares the circle” by showing, through the method of exhaustion, that the area of a circle equals that of a right-angled triangle whose perpendicular equals the radius, and whose base equals the circumference, of the circle. (4) The Quadrature of the Parabola studies, by a form of integral calculus, the area cut off from a parabola by a chord, and the problem of finding the area of an ellipse. (5) On Spirals defines a spiral as the figure made by a point moving from a fixed point at a uniform rate along a straight line which is revolving in a plane at a uniform rate about the same fixed point; and finds the area enclosed by a spiral curve and two radii vectores by methods approximating differential calculus. (6) The Sphere and the Cylinder seeks formulas for the volume and surface area of a pyramid, a cone, a cylinder, and a sphere. (7) On Conoids and Spheroids studies the solids generated by the revolution of conic sections about their axes. (8) The Sand-Reckoner passes from geometry to arithmetic, almost to logarithms, by suggesting that large numbers may be represented by multiples, or “orders,” of 10,000; by this method Archimedes expresses the number of grains of sand which would be needed to fill the universe—assuming, he genially adds, that the universe has a reasonable size. His conclusion, which anyone may verify for himself, is that the world contains not more than sixty-three “ten-million units of the eighth order of numbers”—or, as we should put it, 1068. References to lost works of Archimedes indicate that he had also discovered a way of finding the square root of nonsquare numbers. (9) On Plane Equilibriums applies geometry to mechanics, studies the center of gravity of various bodily configurations, and achieves the oldest extant formulation of scientific statics. (10) On Floating Bodies founds hydrostatics by arriving at mathematical formulas for the position of equilibrium of a floating body. The work begins with the then startling thesis that the surface of any liquid body at rest and in equilibrium is spherical, and that the sphere has the same center as the earth.
for π—the ratio of the circumference to the diameter of a circle—and “squares the circle” by showing, through the method of exhaustion, that the area of a circle equals that of a right-angled triangle whose perpendicular equals the radius, and whose base equals the circumference, of the circle. (4) The Quadrature of the Parabola studies, by a form of integral calculus, the area cut off from a parabola by a chord, and the problem of finding the area of an ellipse. (5) On Spirals defines a spiral as the figure made by a point moving from a fixed point at a uniform rate along a straight line which is revolving in a plane at a uniform rate about the same fixed point; and finds the area enclosed by a spiral curve and two radii vectores by methods approximating differential calculus. (6) The Sphere and the Cylinder seeks formulas for the volume and surface area of a pyramid, a cone, a cylinder, and a sphere. (7) On Conoids and Spheroids studies the solids generated by the revolution of conic sections about their axes. (8) The Sand-Reckoner passes from geometry to arithmetic, almost to logarithms, by suggesting that large numbers may be represented by multiples, or “orders,” of 10,000; by this method Archimedes expresses the number of grains of sand which would be needed to fill the universe—assuming, he genially adds, that the universe has a reasonable size. His conclusion, which anyone may verify for himself, is that the world contains not more than sixty-three “ten-million units of the eighth order of numbers”—or, as we should put it, 1068. References to lost works of Archimedes indicate that he had also discovered a way of finding the square root of nonsquare numbers. (9) On Plane Equilibriums applies geometry to mechanics, studies the center of gravity of various bodily configurations, and achieves the oldest extant formulation of scientific statics. (10) On Floating Bodies founds hydrostatics by arriving at mathematical formulas for the position of equilibrium of a floating body. The work begins with the then startling thesis that the surface of any liquid body at rest and in equilibrium is spherical, and that the sphere has the same center as the earth.
Perhaps Archimedes was led to the study of hydrostatics by an incident almost as famous as Newton’s apple. King Hieron had given to a Syracusan Cellini some gold to be formed into a crown. When the crown was delivered it weighed as much as the gold; but some doubt arose whether the artist had made up part of the weight by using silver, keeping the saved gold for himself. Hieron turned over to Archimedes his suspicion and the crown, presumably stipulating that the one should be resolved without injuring the other. For weeks Archimedes puzzled over the problem. One day, as he stepped into a tub at the public baths, he noticed that the water overflowed according to the depth of his immersion, and that his body appeared to weigh—or press downward—less, the more it was submerged. His curious mind, exploring and utilizing every experience, suddenly formulated the “principle of Archimedes”—that a floating body loses in weight an amount equal to the weight of the water which it displaces. Surmising that a submerged body would displace water according to its volume, and perceiving that this principle offered a test for the crown, Archimedes (if we may believe the staid Vitruvius) dashed out naked into the street and rushed to his dwelling, crying out “Eureka! eureka!”—I have found it! I have found it! Home, he soon discovered that a given weight of silver, since it had more volume per weight than gold, displaced more water, when immersed, than an equal weight of gold. He observed also that the submerged crown displaced more water than a quantity of gold equaling the crown in weight. He concluded that the crown had been alloyed with some metal less dense than gold. By replacing gold with silver in the gold weight which he was using for comparison, until the compound displaced as much water as the crown, Archimedes was able to say just how much silver had been used in the crown, and how much gold had been stolen.
That he had satisfied the curiosity of the King did not mean so much to him as that he had discovered the law of floating bodies, and a method for measuring specific gravity. He made a planetarium representing the sun, the earth, the moon, and the five planets then known (Saturn, Jupiter, Mars, Venus, and Mercury), and so arranging them that by turning a crank one could set all these bodies in motions differing in direction and speed;6 but he probably agreed with Plato that the laws that govern the movements of the heavens are more beautiful than the stars.* In a lost treatise partly preserved in summaries, Archimedes so accurately formulated the laws of the lever and the balance that no advance was made upon his work until A.D. 1586. “Commensurable magnitudes,” said Proposition VI, “will balance at distances inversely proportional to their gravities”8—a useful truth whose brilliant simplification of complex relationships moves the soul of a scientist as the Hermes of Praxiteles moves the artist. Almost intoxicated with the vision of power which he saw in the lever and the pulley, Archimedes announced that if he had a fixed fulcrum to work with he could move anything: “Pa bo, kai tan gan kino” he is reported to have said, in the Doric dialect of Syracuse: “Give me a place to stand on, and I will move the earth.”9 Hieron challenged him to do as well as say, and pointed to the difficulty which his men were experiencing in beaching a large ship in the royal fleet. Archimedes arranged a series of cogs and pulleys in such wise that he alone, sitting at one end of the mechanism, was able to draw the fully loaded vessel out of the water onto the land.10
Delighted with this demonstration, the King asked Archimedes to design some engines of war. It was characteristic of the two men that Archimedes, having designed them, forgot them, and that Hieron, loving peace, never used them. Archimedes, says Plutarch,
possessed so high a spirit, so profound a soul, and such treasures of scientific knowledge, that though these inventions had now obtained for him the renown of more than human sagacity, he yet would not deign to leave behind him any writing on such subjects; but, repudiating as sordid and ignoble . . . every sort of art that lends itself to mere use and profit, he placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life—studies whose superiority to all others is unquestioned, and in which the only doubt can be whether the beauty and grandeur of the subjects examined, or the precision and cogency of the methods and means of proof, most deserve our admiration.11
But when Hieron was dead Syracuse became embroiled with Rome, and the doughty Marcellus assailed it by land and sea. Though Archimedes was now (212) a man of seventy-five, he superintended the defense on both fronts. Behind the walls that protected the harbor he set up catapults able to hurl heavy stones to a considerable distance; their rain of projectiles was so devastating that Marcellus retreated until he could advance by night. But when the ships were seen near the shore the sailors were harassed by bowmen who shot at them through the holes that Archimedes’ aides had pierced in the wall. Moreover, the inventor had arranged within the walls great cranes which, when the Roman vessels came within reach, were turned by cranks and pulleys so as to drop upon the ships heavy weights of stone or lead that sank many of them. Other cranes, armed with gigantic hooks, grasped vessels, lifted them into the air, dashed them against the rocks, or plunged them end-foremost into the sea.*12 Marcellus withdrew his fleet, and put his hopes in an attack by land. But Archimedes bombarded the troops with large stones thrown by catapults to such effect that the Romans fled, saying that they were being opposed by gods; and they refused to advance again.14 “Such a great and marvelous thing,” comments Polybius, “does the genius of one man show itself to be when properly applied. The Romans, strong both by sea and by land, had every hope of capturing the town at once if one old man of Syracuse were removed; as long as he was present they did not venture to attack.”15
Abandoning the idea of taking Syracuse by storm, Marcellus resigned himself to a slow blockade. After a siege of eight months the starving city surrendered. In the slaughter and pillage that followed Marcellus gave orders that Archimedes should not be injured. During the sack a Roman soldier came upon an aged Syracusan absorbed in studying figures that he had traced in the sand. The Roman commanded him to present himself at once to Marcellus. Archimedes refused to go until he had worked out his problem; he “earnestly besought the soldier,” says Plutarch, “to wait a little while, that he might not leave what he was at work upon inconclusive and imperfect, but the soldier, nothing moved by this entreaty, instantly killed him.”16 When Marcellus heard of it he mourned, and did everything in his power to console the relatives of the dead man.17 The Roman general erected to his memory a handsome tomb, on which was engraved, in accordance with the mathematician’s expressed wish, a sphere within a cylinder; to have found formulas for the area and volume of these figures was, in Archimedes’ view, the supreme achievement of his life. He was not far wrong; for to add one significant proposition to geometry is of greater value to humanity than to besiege or defend a city. We must rank Archimedes with Newton, and credit him with “a sum of mathematical achievement unsurpassed by any one man in the world’s history.”18
But for the abundance and cheapness of slaves Archimedes might have been the head of a veritable Industrial Revolution. A treatise on Mechanical Problems wrongly attributed to Aristotle, and a Treatise on Weights wrongly ascribed to Euclid, had laid down certain elementary principles of statics and dynamics a century before Archimedes. Strato of Lampsacus, who succeeded Theophrastus as head of the Lyceum, turned his deterministic materialism to physics, and (about 280) formulated the doctrine that “nature abhors a vacuum.”19 When he added that “a vacuum can be created by artificial means,” he opened the way to a thousand inventions. Ctesibius of Alexandria (ca. 200) studied the physics of siphons (which had been used in Egypt as far back as 1500 B.C.), and developed the force pump, the hydraulic organ, and the hydraulic clock. Archimedes probably improved—and unwittingly gave his name to—the ancient Egyptian water screw, which literally made water flow uphill.20 Philon of Byzantium, about 150, invented pneumatic machines, and various engines of war.21 The steam engine of Heron of Alexandria, which came after the Roman conquest of Greece, brought this period of mechanical development to a climax and close. The philosophical tradition was too strong; Greek thought went back to theory, and Greek industry contented itself with slaves. The Greeks were acquainted with the magnet, and the electrical properties of amber, but they saw no industrial possibilities in these curious phenomena. Antiquity unconsciously decided that it was not worth while to be modern.
III. ARISTARCHUS, HIPPARCHUS, ERATOSTHENES
Greek mathematics owed its Hellenistic stimulus and blossoming to Egypt, Greek astronomy to Babylon. Alexander’s opening of the East led to a resumption and extension of that trade in ideas which, three centuries earlier, had assisted at the birth of Greek science in Ionia. To this fresh contact with Egypt and the Near East we may ascribe the anomaly of Greek science reaching its height in the Hellenistic age, when Greek literature and art were in decline.
Aristarchus of Samos was a bright interregnum in the rule of the geocentric theory over Greek astronomy. He burned with such zeal that he studied almost all its branches, and achieved distinction in many of them.23 In his only extant treatise, On the Sizes and Distances of the Sun and the Moon,* there is no hint of heliocentricism; on the contrary it assumes that the sun and the moon move in circles about the earth. But Archimedes’ Sand-Reckoner explicitly credits Aristarchus with the “hypothesis that the fixed stars and the sun remain unmoved; the earth revolves about the sun in the circumference of a circle, the sun lying in the middle of the orbit”;24 and Plutarch reports that Cleanthes the Stoic held that Aristarchus should be indicted for “putting the Hearth of the Universe” (i.e., the earth) “in motion.”25 Seleucus of Seleucia defended the heliocentric view, but the opinion of the Greek scientific world decided against it. Aristarchus himself seems to have abandoned his hypothesis when he failed to reconcile it with the supposedly circular movements of the heavenly bodies; for all Greek astronomers took it for granted that these orbits were circular. Perhaps a distaste for hemlock moved Aristarchus to be the Galileo as well as the Copernicus of the ancient world.
It was the misfortune of Hellenistic science that the greatest of Greek astronomers attacked the heliocentric theory with arguments that seemed irrefutable before Copernicus. Hipparchus of Nicaea (in Bithynia), despite what seems to us an epoch-making blunder, was a scientist of the highest type—endlessly curious to know, devotedly patient in research, and so carefully accurate in observation and report that antiquity called him “the lover of truth.”26 He touched and adorned nearly every field of astronomy, and fixed its conclusions for seventeen centuries. Only one of his many works remains—a commentary on the Phainomena of Eudoxus and Aratus of Soli; but we know him from Claudius Ptolemy’s Almagest (ca. A.D. 140), which is based upon his researches and calculations; “Ptolemaic astronomy” should be called Hipparchian. He improved, probably on Babylonian models, the astrolabes and quadrants that were the chief astronomical instruments of his time. He invented the method of determining terrestrial positions by lines of latitude and longitude, and tried to organize the astronomers of the Mediterranean world to make observations and measurements that would fix in these terms the location of all important cities; political disturbances frustrated the plan until Ptolemy’s more orderly age. His mathematical studies of astronomic relations led Hipparchus to formulate a table of sines, and thereby to create the science of trigonometry. Helped, no doubt, by the cuneiform records which had been brought from Babylonia, he determined with approximate accuracy the length of the solar, lunar, and sidereal years. He reckoned the solar year as 365¼ days minus 4 minutes and 48 seconds—an error of 6 minutes according to current calculations. His time for a mean lunar month was 29 days, 12 hours, 44 minutes, and 2½ seconds—less than a second away from the accepted figure.27 He computed, with impressive approximation to modern measurements, the synodic periods of the planets, the obliquity of the ecliptic and of the moon’s orbit, the apogee of the sun, and the horizontal parallax of the moon.28 He estimated the distance of the moon from the earth as 250,000 miles—an error of only five per cent.
Armed with all this knowledge, Hipparchus concluded that the geocentric view better explained the data than did the hypothesis of Aristarchus; the heliocentric theory could not stand mathematical analysis except by supposing an elliptical orbit for the earth, and this supposition was so uncongenial to Greek thought that even Aristarchus does not appear to have considered it. Hipparchus verged upon it by his theory of “eccentrics,” which accounted for the apparent irregularities in the orbital velocities of the sun and the moon by suggesting that the centers of the solar and lunar orbits were slightly to one side of the earth. So near did Hipparchus come to being the greatest theorist, as well as the greatest observer, among ancient astronomers.
Watching the sky night after night, Hipparchus was surprised one evening by the appearance of a star where he was sure there had been none before. To certify later changes he made, about 129 B.C., a catalogue, a map, and a globe of the heavens, giving the positions of 1080 fixed stars in terms of celestial latitude and longitude—an immense boon to subsequent students of the sky. Comparing his chart with that which Timochares had made 166 years before, Hipparchus calculated that the stars had shifted their apparent position some two degrees in the interval. On this basis he made the subtlest of his discoveries*—the precession of the equinoxes—the slight advance, day by day, of the moment when the equinoctial points come to the meridian,† He calculated the precession as thirty-six seconds per year; the current estimate is fifty.
We have displaced from his chronological position between Aristarchus and Hipparchus a scholar whose ecumenical erudition won him the nicknames of Pentathlos and Beta—because he attained distinction in many fields, and ranked second only to the best in each. Tradition gave Eratosthenes of Cyrene exceptional teachers: Zeno the Stoic, Arcesilaus the skeptic, Callimachus the poet, Lysanias the grammarian. By the age of forty his reputation for varied knowledge was so great that Ptolemy III made him head of the Alexandrian Library. He wrote a volume of verse, and a history of comedy. His Chronographia sought to determine the dates of the major events in Mediterranean history. He wrote mathematical monographs, and devised a mechanical method for finding mean proportions in continued proportion between two straight lines. He measured the obliquity of the ecliptic at 23° 51′, an error of one half of one per cent. His greatest achievement was his calculation of the earth’s circumference as 24,662 miles;30 we compute it at 24,847. Observing that at noon on the summer solstice the sun at Syene shone directly upon the deep surface of a narrow well, and learning that at the same moment the shadow of an obelisk at Alexandria, some five hundred miles north, showed the sun to be approximately 7½° away from the zenith as measured on the meridian of longitude that connected the two cities, he concluded that an arc of 7½° on the earth’s circumference equaled five hundred miles, and that the entire circumference would equal 360÷7.5×500, or 24,000 miles.
Having measured the earth, Eratosthenes proceeded to describe it. His Geographica brought together the reports of Alexander’s surveyors, of travelers like Megasthenes, voyagers like Nearchus, and explorers like Pytheas of Massalia, who, about 320, had sailed around Scotland to Norway, and perhaps to the Arctic Circle.31 Eratosthenes did not merely depict the physical features of each region, he sought to explain them through the action of water, fire, earthquake, or volcanic eruption.32 He bade the Greeks abandon their provincial division of mankind into Hellenes and barbarians; men should be divided not nationally but individually; many Greeks, he thought, were scoundrels, many Persians and Hindus were refined, and the Romans had shown a greater aptitude than the Greeks for social order and competent government.33 He knew little of northern Europe or northern Asia, less of India south of the Ganges, nothing of south Africa; but he was, so far as we know, the first geographer to mention the Chinese. “If,” said another significant passage, “the extent of the Atlantic Ocean were not an obstacle, we might easily pass by sea from Iberia (Spain) to India, keeping in the same parallel.”34
IV. THEOPHRASTUS, HEROPHILUS, ERASISTRATUS
Zoology never rose again in antiquity to the level that it had reached in Aristotle’s History of Animals. Probably by an agreed division of labor his successor Theophrastus wrote a classic treatise, The History of Plants, and a more theoretical discussion called The Causes of Plants. Theophrastus loved gardening, and knew every aspect of his subject. In many ways he was more scientific than his master, more careful of his facts, and more orderly in his exposition; a book without classification, he said, was as untrustworthy as an unbridled horse.35 He divided all plants into trees, bushes, shrubs, and herbs, and distinguished the chief parts of a plant as root, stem, branch, twig, leaf, flower, and fruit—a classification not improved on till A.D. 1561.36 “A plant,” he wrote, “has the power of germination in all its parts, for it has life in them all. . . . The methods of generation of plants are these: spontaneous, from a seed, a root, a piece torn off, a branch, a twig, pieces of wood cut up small, or from the trunk itself.”37 He had no clear idea of sexual reproduction in plants, except in a few species like the fig tree or the date palm; here he followed the Babylonians in describing fertilization and caprification. He discussed the geographical distribution of plants, their industrial uses, and the climatic conditions most conducive to their health. He studied the minutiae of half a thousand species with an accuracy of detail astonishing in an age that had no microscope. Twenty centuries before Goethe he recognized that the flower is a metamorphosed leaf.38 He was a naturalist in more ways than one, stoutly rejecting the supernatural explanations current in his day for certain curiosities of botany.39 He had all the inquisitiveness of a scientist, and did not think it beneath his dignity as a philosopher to write monographs on stones, minerals, weather, winds, weariness, geometry, astronomy, and the physical theories of the pre-Socratic Greeks.40 “If there had been no Aristotle,” says Sarton, “this period would have been called the time of Theophrastus.”41
Theophrastus’ ninth “book” summarized all that the Greeks knew about the medicinal properties of plants. One passage hinted at anesthesia in describing “dittany, a plant especially useful for labor in women; people say that either it makes labor easy, or it stops the pains.”42 Medicine progressed rapidly in this age, perhaps because it had to keep pace with the novel and multiplying diseases of a complex urban civilization. The Greek study of Egyptian medical lore stimulated a fresh advance. The Ptolemies were ruthlessly helpful; they not only permitted the dissection of animals and cadavers, but turned over some condemned criminals for vivisection.43 Under these encouragements human anatomy became a science, and the absurdities into which Aristotle had fallen were substantially reduced.
Herophilus of Chalcedon, working at Alexandria about 285, dissected the eye and gave a good account of the retina and the optic nerves. He dissected the brain, described the cerebrum, the cerebellum, and the meninges, left his name in the torcular Herophili* and restored the brain to honor as the seat of thought. He understood the role of the nerves, originated their division into sensory and motor, and separated the cranial from the spinal nerves. He distinguished arteries from veins, discerned the function of the arteries as carrying blood from the heart to various parts of the body, and in effect discovered the circulation of the blood nineteen centuries before Harvey.44 Following a suggestion of the Coan physician Praxagoras, he included the taking of the pulse in diagnosis, and used a water clock to measure its frequency. He dissected and described the ovaries, the uterus, the seminal vesicles, and the prostate gland; he studied the liver and the pancreas, and gave to the duodenum the name that it still bears.45“Science and art,” wrote Herophilus, “have nothing to show, strength is incapable of effort, wealth is useless, and eloquence is powerless, where there is no health.”46
Herophilus was, so far as we can now judge, the greatest anatomist of antiquity, and Erasistratus was the greatest physiologist. Born in Ceos, Erasistratus studied in Athens, and practiced medicine in Alexandria about 258 B.C. He distinguished more carefully than Herophilus between cerebrum and cerebellum, and made experiments on living subjects to study the operation of the brain. He described and explained the working of the epiglottis, the lacteal vessels of the mesentery, and the aortic and pulmonary valves of the heart. He had some notion of basal metabolism, for he devised a crude respiration calorimeter47 Every organ, said Erasistratus, is connected with the rest of the organism in three ways—by artery, vein, and nerve. He sought to account for all physiological phenomena by natural causes, rejecting any reference to mystical entities. He discarded the humoral theory of Hippocrates, which Herophilus had retained. He conceived the art of medicine as prevention through hygiene rather than as cure through therapy; he opposed the frequent use of drugs and bloodletting, and relied upon diet, bathing, and exercise.48
Such men made Alexandria the Vienna of the ancient medical world. But there were great schools of medicine also at Tralles, Miletus, Ephesus, Pergamum, Taras, and Syracuse. Many cities had a municipal medical service; the physicians so employed received a modest salary, but were honored for making no distinction between rich and poor, free and slave, and for devoting themselves to their work at any time and risk. Apollonius of Miletus fought the plague in near-by islands without reward; when all the doctors of Cos were laid low by an epidemic which they had labored to control, others came to their rescue from neighboring towns. Many public decrees of gratitude were issued to Hellenistic physicians; and though ancient jests railed at mercenary incompetence, the great profession kept high that standard of ethics which had come down to it from Hippocrates as its most precious inheritance.
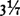 and
and 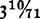 for π—the ratio of the circumference to the diameter of a circle—and “squares the circle” by showing, through the method of exhaustion, that the area of a circle equals that of a right-angled triangle whose perpendicular equals the radius, and whose base equals the circumference, of the circle. (4) The Quadrature of the Parabola studies, by a form of integral calculus, the area cut off from a parabola by a chord, and the problem of finding the area of an ellipse. (5) On Spirals defines a spiral as the figure made by a point moving from a fixed point at a uniform rate along a straight line which is revolving in a plane at a uniform rate about the same fixed point; and finds the area enclosed by a spiral curve and two radii vectores by methods approximating differential calculus. (6) The Sphere and the Cylinder seeks formulas for the volume and surface area of a pyramid, a cone, a cylinder, and a sphere. (7) On Conoids and Spheroids studies the solids generated by the revolution of conic sections about their axes. (8) The Sand-Reckoner passes from geometry to arithmetic, almost to logarithms, by suggesting that large numbers may be represented by multiples, or “orders,” of 10,000; by this method Archimedes expresses the number of grains of sand which would be needed to fill the universe—assuming, he genially adds, that the universe has a reasonable size. His conclusion, which anyone may verify for himself, is that the world contains not more than sixty-three “ten-million units of the eighth order of numbers”—or, as we should put it, 1068. References to lost works of Archimedes indicate that he had also discovered a way of finding the square root of nonsquare numbers. (9) On Plane Equilibriums applies geometry to mechanics, studies the center of gravity of various bodily configurations, and achieves the oldest extant formulation of scientific statics. (10) On Floating Bodies founds hydrostatics by arriving at mathematical formulas for the position of equilibrium of a floating body. The work begins with the then startling thesis that the surface of any liquid body at rest and in equilibrium is spherical, and that the sphere has the same center as the earth.
for π—the ratio of the circumference to the diameter of a circle—and “squares the circle” by showing, through the method of exhaustion, that the area of a circle equals that of a right-angled triangle whose perpendicular equals the radius, and whose base equals the circumference, of the circle. (4) The Quadrature of the Parabola studies, by a form of integral calculus, the area cut off from a parabola by a chord, and the problem of finding the area of an ellipse. (5) On Spirals defines a spiral as the figure made by a point moving from a fixed point at a uniform rate along a straight line which is revolving in a plane at a uniform rate about the same fixed point; and finds the area enclosed by a spiral curve and two radii vectores by methods approximating differential calculus. (6) The Sphere and the Cylinder seeks formulas for the volume and surface area of a pyramid, a cone, a cylinder, and a sphere. (7) On Conoids and Spheroids studies the solids generated by the revolution of conic sections about their axes. (8) The Sand-Reckoner passes from geometry to arithmetic, almost to logarithms, by suggesting that large numbers may be represented by multiples, or “orders,” of 10,000; by this method Archimedes expresses the number of grains of sand which would be needed to fill the universe—assuming, he genially adds, that the universe has a reasonable size. His conclusion, which anyone may verify for himself, is that the world contains not more than sixty-three “ten-million units of the eighth order of numbers”—or, as we should put it, 1068. References to lost works of Archimedes indicate that he had also discovered a way of finding the square root of nonsquare numbers. (9) On Plane Equilibriums applies geometry to mechanics, studies the center of gravity of various bodily configurations, and achieves the oldest extant formulation of scientific statics. (10) On Floating Bodies founds hydrostatics by arriving at mathematical formulas for the position of equilibrium of a floating body. The work begins with the then startling thesis that the surface of any liquid body at rest and in equilibrium is spherical, and that the sphere has the same center as the earth.