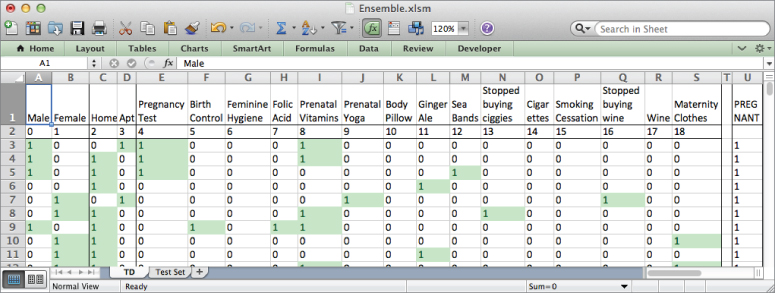
Figure 7.1 The TD tab houses the data from Chapter 6.
On the American version of the popular TV show The Office, the boss, Michael Scott, buys pizza for his employees. Everyone groans when they learn that he has unfortunately bought pizza from Pizza by Alfredo instead of Alfredo's Pizza. Although it's cheaper, apparently pizza from Pizza by Alfredo is awful.
In response to their protests, Michael asks his employees a question: is it better to have a small amount of really good pizza or a lot of really bad pizza?
For many practical artificial intelligence implementations, the answer is arguably the latter. In the previous chapter, you built a single, good model for predicting pregnant households shopping at RetailMart. What if instead, you got democratic? What if you built a bunch of admittedly crappy models and let them vote on whether a customer was pregnant? The vote tally would then be used as a single prediction.
This type of approach is called ensemble modeling, and as you'll see, it turns simple observations into gold.
You'll be going over a type of ensemble model called bagged decision stumps, which is very close to an approach used constantly in industry called the random forest model. In fact, it's very nearly the approach I use daily in my own life here at MailChimp.com to predict when a user is about to send some spam.
After bagging, you'll investigate another awesome technique called boosting. Both of these techniques find creative ways to use the training data over and over and over again to train up an entire ensemble of classifiers. There's an intuitive feel to these approaches that's reminiscent of naïve Bayes—a stupidity that, in aggregate, is smart.
This chapter's gonna move quickly, because you'll use the RetailMart data from Chapter 6. Using the same data will give you a sense of the differences in these two models' implementations from the regression models in the previous chapter. The modeling techniques demonstrated in this chapter were invented more recently. They're somewhat more intuitive, and yet, are some of the most powerful off the shelf AI technologies we have today.
Also, we'll be building ROC curves identical to those from Chapter 6, so I won't be spending much time explaining performance metric calculations. See Chapter 6 if you really want to understand concepts like precision and recall.
Starting off, the workbook available for download has a sheet called TD which includes the training data from Chapter 6 with the dummy variables already set up properly (for more on this see Chapter 6). Also, the features have been numbered 0 to 18 in row 2. This will come in handy with recordkeeping later (see Figure 7.1).
Figure 7.1 The TD tab houses the data from Chapter 6.

The workbook also includes the Test Set tab from Chapter 6.
You will try to do exactly what you did in Chapter 6 with this data—predict the values in the PREGNANT column using the data to the left of it. Then you'll verify the accuracy on the holdout set.
Bagging is a technique used to train multiple classifiers (an ensemble if you will) without them all being trained on the exact same set of training data. Because if you trained the classifiers on the same data, they'd look identical; you want a variety of models, not a bunch of copies of the same model. Bagging lets you introduce some variety in a set of classifiers where there otherwise wouldn't be.
In the bagging model you'll be building, the individual classifiers will be decision stumps. A decision stump is nothing more than a single question you ask about the data. Depending on the answer, you say that the household is either pregnant or not. A simple classifier such as this is often called a weak learner.
For example, in the training data, if you count the number of times a pregnant household purchased folic acid by highlighting H3:H502 and summing with the summary bar, you'd find that 104 pregnant households made the purchase before giving birth. On the other hand, only two not-pregnant customers bought folic acid.
So there's a relationship between buying folic acid supplements and being pregnant. You can use that simple relationship to construct the following weak learner:
Did the household buy folic acid? If yes, then assume they're pregnant. If no, then assume they're not pregnant.
This predictor is visualized in Figure 7.2.
Figure 7.2 The folic acid decision stump
The stump in Figure 7.2 divides the set of training records into two subsets. Now, you might be thinking that that decision stump makes perfect sense, and you're right, it does. But it ain't perfect. After all, there are nearly 400 pregnant households in the training data that didn't buy folic acid but who would be classified incorrectly by the stump.
It's still better than not having a model at all, right?
Undoubtedly. But the question is how much better is the stump than not having a model. One way to evaluate that is through a measurement called node impurity.
Node impurity measures how often a chosen customer record would be incorrectly labeled as pregnant or not-pregnant if it were assigned a label randomly, according to the distribution of customers in its decision stump subset.
For instance, you could start by shoving all 1,000 training records into the same subset, which is to say, start without a model.
The probability that you'll pull a pregnant person from the heap is 50 percent. And if you label them randomly according to the 50/50 distribution, you have a 50 percent chance of guessing the label correctly.
Thus, you have a 50%*50% = 25 percent chance of pulling a pregnant customer and appropriately guessing they're pregnant. Similarly, you have a 25 percent chance of pulling a not-pregnant customer and guessing they're not pregnant. Everything that's not those two cases is just some version of an incorrect guess.
That means I have a 100% – 25% – 25% = 50 percent chance of incorrectly labeling a customer. So you would say that the impurity of my single starting node is 50 percent.
The folic acid stump splits this set of 1,000 cases into two groups—894 folks who didn't buy folic acid and 106 folks who did. Each of those subsets will have its own impurity, so if you average the impurities of those two subsets (adjusting for their size difference), you can tell how much the decision stump has improved your situation.
For those 894 customers placed into the not-pregnant bucket, 44 percent of them are pregnant and 56 percent are not. This gives an impurity calculation of 100% – 44%^2 – 56%^2 = 49 percent. Not a whole lot of improvement.
But for the 106 customers placed in the pregnant category, 98 percent of them are pregnant and 2 percent are not. This gives an impurity calculation of 100% – 98%^2 – 2%^2 = 4 percent. Very nice. Averaging those together, you find that the impurity for the entire stump is 44 percent. That's better than a coin flip!
Figure 7.3 shows the impurity calculation.
Figure 7.3 Node impurity for the folic acid stump

A single decision stump isn't enough. What if you had scads of them, each trained on different pieces of data and each with an impurity slightly lower than 50 percent? Then you could allow them to vote. Based on the percentage of stumps that vote pregnant, you could decide to call a customer pregnant.
But you need more stumps.
Well, you've trained one on the Folic Acid column. Why not just do the same thing on every other feature?
You have only 19 features, and frankly, some of those features, like whether the customer's address is an apartment, are pretty terrible. So you'd be stuck with 19 stumps of dubious quality.
It turns out that through bagging, you can make as many decision stumps as you like. Bagging will go something like this:
You need to be able to select a random set of rows and columns from the training data. And the easiest way to do that is to shuffle the rows and columns like a deck of cards and then select what you need from the top left of the table.
To start, copy A2:U1002 from the TD tab into the top of a new tab called TD_BAG (you won't need the feature names, just their index values from row 2). The easiest way to shuffle TD_BAG will be to add an extra column and an extra row next to the data filled with random numbers (using the RAND() formula). Sorting by the random values from top to bottom and left to right and then skimming the amount you want off the upper left of the table gives you a random sample of rows and features.
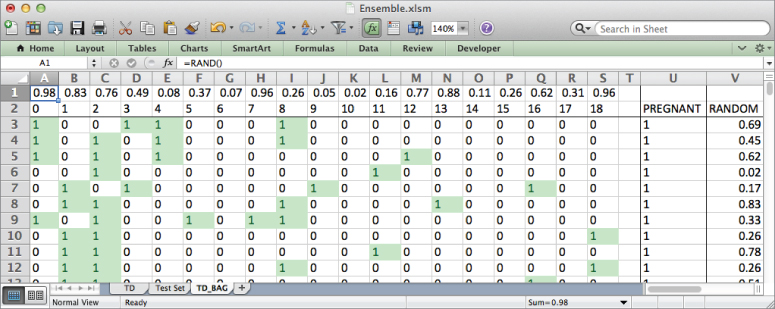
Insert a row above the feature indexes and add the RAND() formula to row 1 (A1:S1) and to column V (V3:V1002). The resulting spreadsheet then looks like Figure 7.4. Note that I've titled column V as RANDOM.
Figure 7.4 Adding random numbers to the top and side of the data
Sort the columns and rows randomly. Start with the columns, because side-to-side sorting is kind of funky. To shuffle the columns, highlight columns A through S. Don't highlight the PREGNANT column, because that's not a feature; it's the dependent variable.
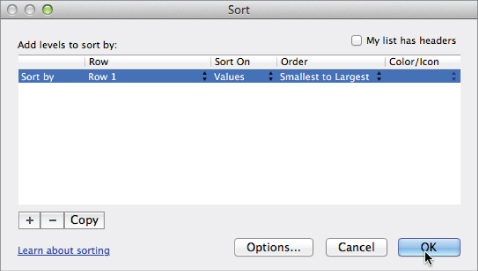
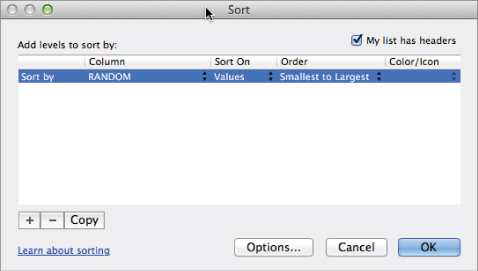
Open the custom sort window (see Chapter 1 for a discussion on custom sorting). From the Sort window (Figure 7.5), press the Options button and select to sort left to right in order to sort the columns. Make sure Row 1, which is the row with the random numbers, is selected as the row to sort by. Also, confirm that the My List Has Headers box is unchecked since you have no headers in the horizontal direction.
Figure 7.5 Sorting from left to right
Press OK. You'll see the columns on the sheet reorder themselves.
Now you need to do the same thing to the rows. This time around, select the range A2:V1002, including the PREGNANT column so that it remains tied to its data while excluding the random numbers at the top of the sheet.
Access the Custom Sort window again, and under the Options section, select to sort from top to bottom this time.
Make sure the My List Has Headers box is checked this time around, and then select the RANDOM column from the drop-down. The Sort window should look like Figure 7.6.
Figure 7.6 Sorting from top to bottom
Now that you've sorted your training data randomly, the first four columns and the first 666 rows form a rectangular random sample that you can grab. Create a new tab called RandomSelection. To pull out the random sample, you point the cell in A1 to the following:
=TD_BAG!A2
And then copy that formula through D667.
You can get the PREGNANT values next to the sample, by mapping them straight into column E. E1 points to cell U2 from the previous tab:
=TD_BAG!U2
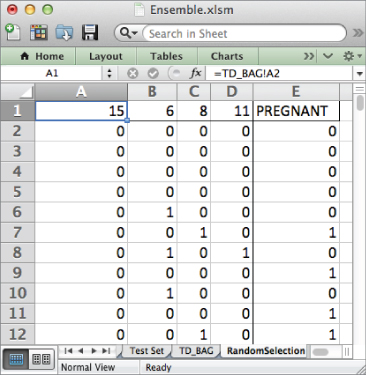
Just double-click that formula to send it down the sheet. Once you complete this, you're left with nothing but the random sample from the data (see Figure 7.7). Note that since the data is sorted randomly, you'll likely end up with four different feature columns.
Figure 7.7 Four random columns and a random two-thirds of the rows
And what's cool is that if you go back to the TD_BAG tab and sort again, this sample will automatically update!
When looking at any one of these four features, there are only four things that can happen between a single feature and the dependent PREGNANT variable:
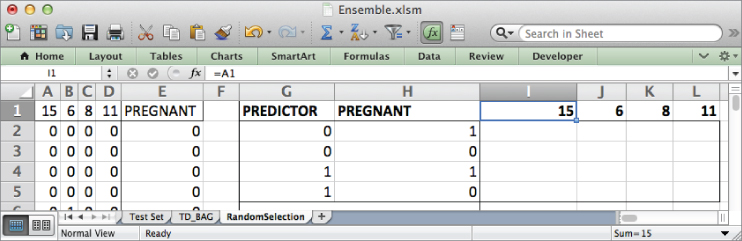
You need to get a count of the number of training rows that fall into each of these cases in order to build a stump on the feature similar to that pictured in Figure 7.2. To do this, enumerate the four combinations of 0s and 1s in G2:H5. Set I1:L1 to equal the column indexes from A1:D1.
The spreadsheet then looks like Figure 7.8.
Figure 7.8 Four possibilities for the training data
Once you've set up this small table, you need to fill it in by getting counts of the training rows whose values match the combination of predictor and pregnant values specified to the left. For the upper-left corner of the table (the first feature in my random sample ended up being number 15), you can count the number of training rows where feature 15 is a 0 and the PREGNANT column is a 1 using the following formula:
=COUNTIFS(A$2:A$667,$G2,$E$2:$E$667,$H2)
The COUNTIFS() formula allows you to count rows that match multiple criteria, hence the S at the end of IFS. The first criterion looks at the feature number 15 range (A2:A667) and checks for rows that are identical to the value in G2 (0), whereas the second criterion looks at the PREGNANT range (E2:E667) and checks for rows that are identical to the value in H2 (1).
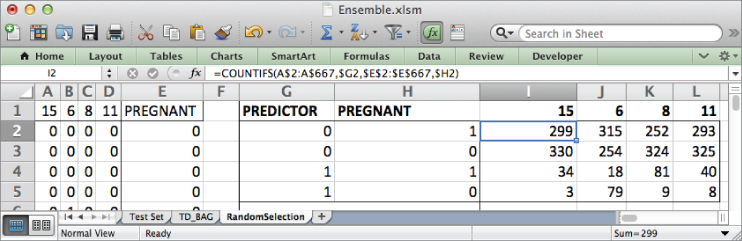
Copy this formula into the rest of the cells in the table to get counts for each case (see Figure 7.9).
Figure 7.9 Feature/response pairings for each of the features in the random sample
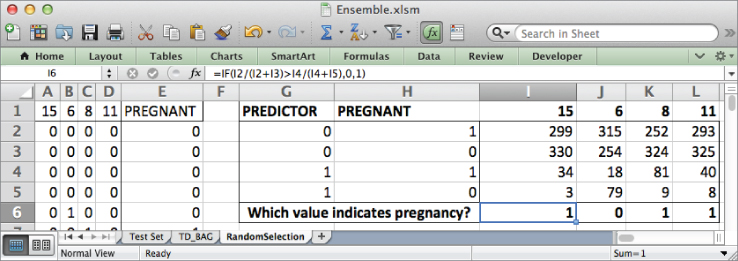
If you were going to treat each of these features as a decision stump, which value for the feature would indicate pregnancy? It'd be the value with the highest concentration of pregnant customers in the sample.
So in row 6 below the count values you can compare these two ratios. In I6 place the formula:
=IF(I2/(I2+I3) I4/(I4+I5),0,1)
If the ratio of pregnant customers associated with the 0 value for the feature (I2/(I2+I3)) is larger than that associated with 1 (I4/(I4+I5)), then 0 is predictive of pregnancy in this stump. Otherwise, 1 is. Copy this formula across through column L. This gives the sheet shown in Figure 7.10.
Figure 7.10 Calculating which feature value is associated with pregnancy
Using the counts in rows 2 through 5, you can calculate the impurity values for the nodes of each decision stump should you choose to split on that feature.
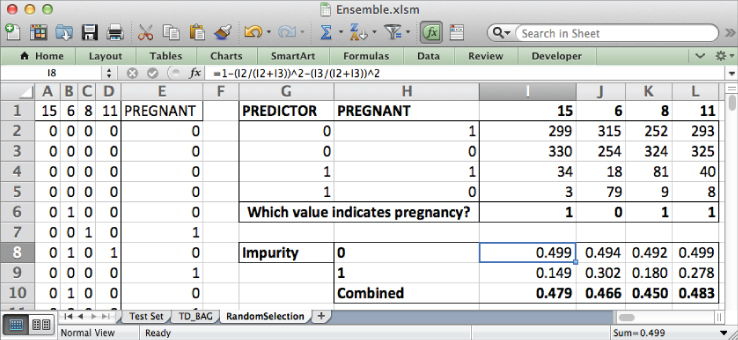
Let's insert the impurity calculations on row 8 below the case counts. Just as in Figure 7.3, you need to calculate an impurity value for the training cases that had a feature value of 0 and average it with those that had a value of 1.
If you use the first feature (number 15 for me), 299 pregnant folks and 330 not-pregnant folks ended up in the 0 node, so the impurity is 100% – (299/629)^2 – (330/629)^2, which can be entered in the sheet in cell I8 as follows:
=1-(I2/(I2+I3))^2-(I3/(I2+I3))^2
Likewise, the impurity for the 1 node can be written as follows:
=1-(I4/(I4+I5))^2-(I5/(I4+I5))^2
They are combined in a weighted average by multiplying each impurity times the number of training cases in its node, summing them, and dividing by the total number of training cases, 666:
=(I8*(I2+I3)+I9*(I4+I5))/666
You can then drag these impurity calculations across all four features yielding combined impurity values for each of the possible decision stumps, as shown in Figure 7.11.
Figure 7.11 Combined impurity values for four decision stumps
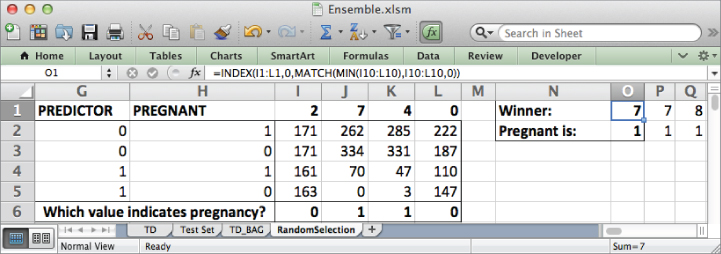
Looking over the impurity values, for my workbook (yours will likely be different due to the random sort), the winning feature is number 8 (looking back at the TD sheet, this is Prenatal Vitamins) with an impurity of 0.450.
All right, so prenatals won on this sample for me. You probably got a different winner, which you should record somewhere.
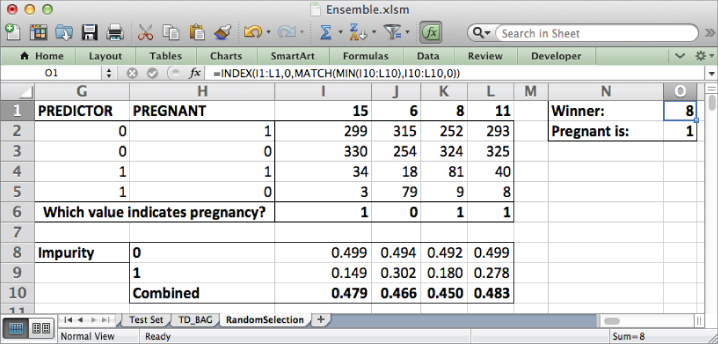
Label cells N1 and N2 as Winner and Pregnant Is. You'll save the winning stump in column O. Start with saving the winning column number in cell O1. This would be the value in I1:L1 that has the lowest impurity (in my case that's 8). You can combine the MATCH and INDEX formulas to do this lookup (see Chapter 1 for more on these formulas):
=INDEX(I1:L1,0,MATCH(MIN(I10:L10),I10:L10,0))
MATCH(MIN(I10:L10),I10:L10,0) finds which column has the minimum impurity on row 10 and hands it to INDEX. INDEX locates the appropriate winning feature label.
Similarly, in O2 you can put whether 0 or 1 is associated with pregnancy by finding the value on row 6 from the column with the minimum impurity:
=INDEX(I6:L6,0,MATCH(MIN(I10:L10),I10:L10,0)
The winning decision stump and its pregnancy-associated node are then called out, as pictured in Figure 7.12.
Figure 7.12 The winner's circle for the four decision stumps
Phew! I know that was a lot of little steps to create one stump. But now that all the formulas are in place, creating the next couple hundred will be a lot easier.
You can create a second one real quick. But before you do, save the stump you just made. To do that, just copy and paste the values in O1:O2 over to the right into P1:P2.
Then to create a new stump, flip back to the TD_BAG tab and shuffle the rows and columns again.
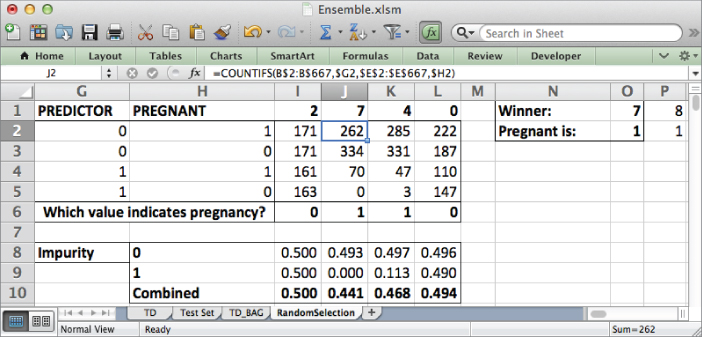
Click back on the RandomSelection tab. Voila! The winner has changed. In my case, it's folic acid, and the value associated with pregnancy is 1 (see Figure 7.13). The previous stump is saved over to the right.
Figure 7.13 Reshuffling the data yields a new stump.
To save this second stump, right-click column P and select Insert to shift the first stump to the right. Then paste the new stump's values in column P. The ensemble now looks like Figure 7.14.
Figure 7.14 And then there were two.
Well, that second one sure took less time than the first. So here's the thing …
Let's say you want to shoot for 200 stumps in the ensemble model. All you have to do is repeat these steps another 198 times. Not impossible, but annoying.
Why don't you just record a macro of yourself doing it and then play the macro back? As it turns out, this shuffling operation is perfect for a macro.
For those of you who have never recorded a macro, it's nothing more than recording a series of repetitive button presses so you can play them back later instead of giving yourself carpal tunnel syndrome.
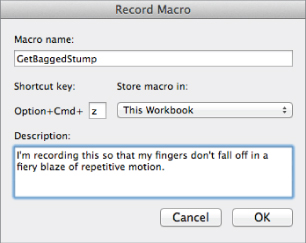
So hop on up to View &cmdarr; Macros (Tools &cmdarr; Macro in Mac OS) and select Record New Macro.
Pressing Record will open a window where you can name your macro something like GetBaggedStump. And for convenience sake, let's associate a shortcut key with the macro. I'm on a Mac so my shortcut keys begin with Option+Cmd, and I'm going to throw in a z into the shortcut box, because that's the kind of mood I'm in today (see Figure 7.15).
Figure 7.15 Getting ready to record a macro
Press OK to get recording. Here are the steps that'll record a full decision stump:
Go to View &cmdarr; Macro &cmdarr; Stop Recording (Tools &cmdarr; Macro &cmdarr; Stop Recording in Excel 2011 for Mac) to end the recording.
You should now be able to generate a new decision stump with a single shortcut key press to activate the macro. Hold on while I go click this thing about 198 hundred times . . .
That's bagging! All you do is shuffle the data, grab a subset, train a simple classifier, and go again. And once you have a bunch of classifiers in your ensemble, you're ready to make predictions.
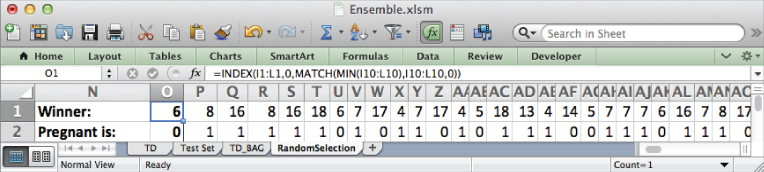
Once you've run the decision stump macro a couple hundred times, the RandomSelection sheet should look like Figure 7.16 (your stumps will likely differ).
Figure 7.16 The 200 decision stumps
Now that you have your stumps, it's time to send your test set data through the model. Create a copy of the Test Set tab and name it TestBag.
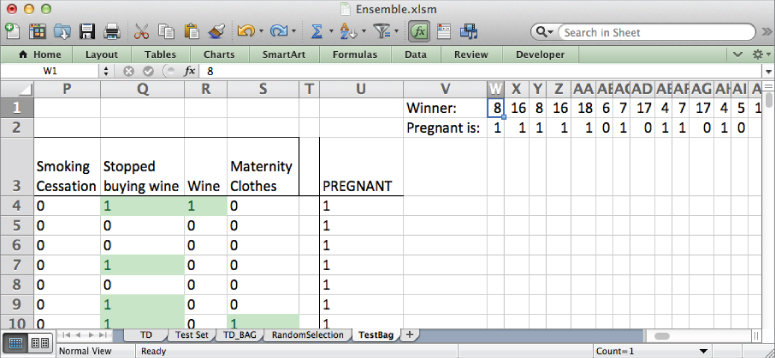
Moving over to the TestBag tab, insert two blank rows at the top of the sheet to make room for your stumps.
Paste the stump values from the RandomSelection tab (P1:HG2 if you've got 200 of them) onto the TestBag tab starting in column W. This gives the sheet shown in Figure 7.17.
Figure 7.17 Stumps added to the TestBag tab
You can run each row in the Test Set through each stump. Start by running the first row of data (row 4) through the first stump in column W. You can use the OFFSET formula to look up the value from the stump column listed in W1, and if that value equals the one in W2, then the stump predicts a pregnant customer. Otherwise, the stump predicts non-pregnancy. The formula looks like this:
=IF(OFFSET($A4,0,W$1)=W$2,1,0)
This formula can be copied across all stumps and down the sheet (note the absolute references). This gives the sheet shown in Figure 7.18.
Figure 7.18 Stumps evaluated on the TestBag set
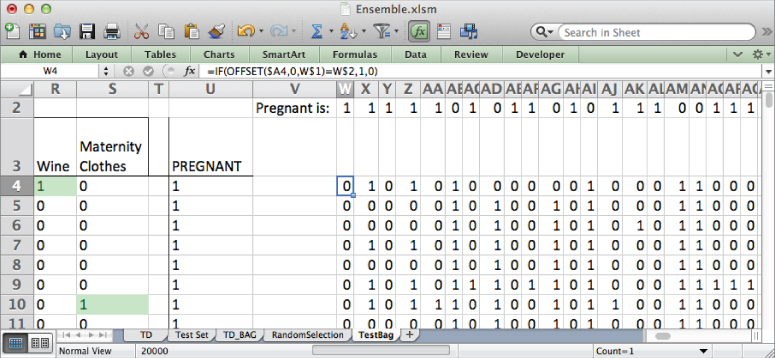
In column V, take the average of the rows to the left in order to obtain a class probability for pregnancy. For example, in V4 if you have 200 stumps, you'd use:
=AVERAGE(W4:HN4)
Copy this down column V to get predictions for each row in the test set as shown in Figure 7.19.
Figure 7.19 Predictions for each row
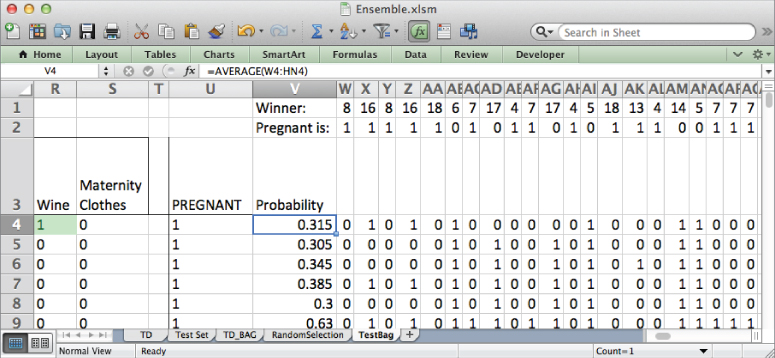
You can evaluate these predictions using the same performance measures used in Chapter 6. I won't dwell on these calculations since the technique is exactly the same as that in Chapter 6. First, create a new tab called PerformanceBag. In the first column, just as in Chapter 6, calculate the maximum and minimum predictions. For my 200 stumps, that range comes out to 0.02 to 0.75.
In column B, place a range of cutoff values from the minimum to the maximum (in my case, I incremented by 0.02). Precision, specificity, false positive rate, and recall can all then be calculated in the same way as Chapter 6 (flip back to Chapter 6 for the precise details).
This gives the sheet shown in Figure 7.20.
Figure 7.20 Performance metrics for bagging
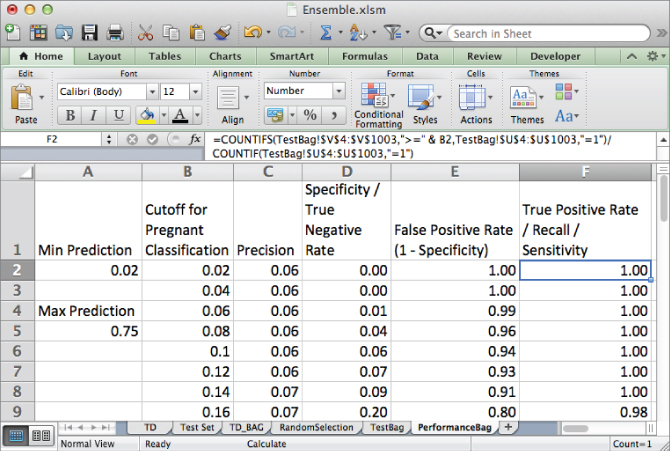
Note that for a prediction cutoff of 0.5, that is, with half of the stumps voting pregnant, you can identify 33 percent of pregnant customers with only a 1 percent false positive rate (your mileage may vary due to the random nature of the algorithm). Pretty sweet for some simple stumps!
You can also insert a ROC curve using the false positive rate and true positive rate (columns E and F) just as you did in Chapter 6. For my 200 stumps, I got Figure 7.21.
Figure 7.21 The ROC Curve for Bagged Stumps
While this bagged stumps model is supported by industry standard packages like R's randomForest package, it's important to call out two differences between this and typical random forest modeling settings:
Moving the conversation beyond model accuracy, here are some advantages to the bagging approach:
The models we use at MailChimp for predicting spam and abuse are random forest models, which we train in parallel using around 10 billion rows of raw data. That's not going to fit in Excel, and I sure as heck wouldn't use a macro to do it!
No, I use the R programming language with the randomForest package, which I would highly recommend learning about as a next step if you want to take one of these models into production at your organization. Indeed, the model in this chapter can be achieved by the randomForest package merely by turning off sampling with replacement and setting the maximum nodes in the decision trees to 2 (see Chapter 10).
What was the reason behind doing bagging, again?
If you trained up a bunch of decision stumps on the whole dataset over and over again, they'd be identical. By taking random selections of the dataset, you introduce some variety to your stumps and end up capturing nuances in the training data that a single stump never could.
Well, what bagging does with random selections, boosting does with weights. Boosting doesn't take random portions of the dataset. It uses the whole dataset on each training iteration. Instead, with each iteration, boosting focuses on training a decision stump that resolves some of the sins committed by the previous decision stumps. It works like this:
Some of this may seem a bit vague, but the process will become abundantly clear in a spreadsheet. Off to the data!
In boosting, each feature is a possible stump on every iteration. You won't be selecting from four features this time.
To start, create a tab called BoostStumps. And on it, paste the possible feature/response value combinations from G1:H5 of the RandomSelection tab.
Next to those values, paste the feature index values (0–18) in row 1. This gives the sheet shown in Figure 7.22.
Figure 7.22 The initial portions of the BoostStumps tab
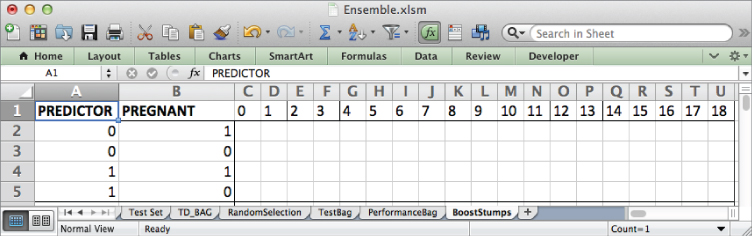
Below each index, just as in the bagging process, you must sum up the number of training set rows that fall into each of the four combinations of feature value and independent variable value listed in columns A and B.
Start in cell C2 (feature index 0) by summing the number of training rows that have a 0 for the feature value and also are pregnant. This can be counted using the COUNTIFS formula:
=COUNTIFS(TD!A$3:A$1002,$A2,TD!$U$3:$U$1002,$B2)
The use of absolute references allows you to copy this formula through U5. This gives the sheet shown in Figure 7.23.
Figure 7.23 Counting up how each feature splits the training data
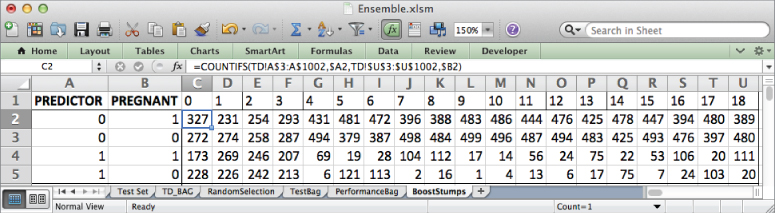
And just as in the case of bagging, in C6 you can find the value associated with pregnancy for feature index 0 by looking at the pregnancy ratios associated with a feature value of 0 and a feature value of 1:
=IF(C2/(C2+C3)>C4/(C4+C5),0,1)
This too may be copied through column U.
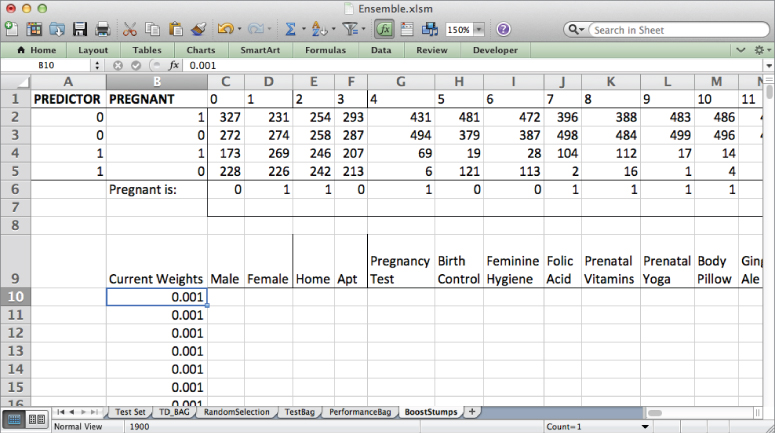
Now, in column B enter in the weights for each data point. Begin in B9 with the label Current Weights, and below that through B1009 put in a 0.001 for each of the thousand training rows. Across row 9, paste the feature names from the TD sheet, just to keep track of each feature.
This gives the sheet shown in Figure 7.24.
Figure 7.24 Weights for each training data row
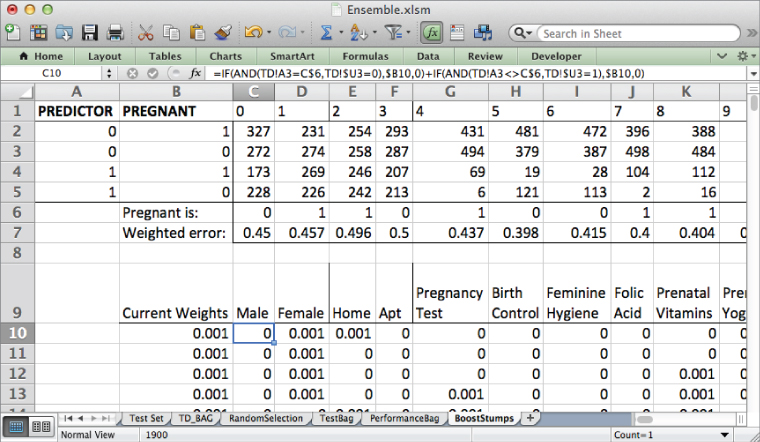
For each of these possible decision stumps, you need to calculate its weighted error rate. This is done by locating the training rows that are miscategorized and penalizing each according to its weight.
For instance in C10, you can look back at the first training row's data for feature index 0 (A3 on the TD tab), and if it matches the pregnancy indicator in C6, then you get a penalty (the weight in cell B10) if the row is not pregnant. If the feature value does not match C6, then you get a penalty if the row is pregnant. This gives the following two IF statements:
=IF(AND(TD!A3=C$6,TD!$U3=0),$B10,0)+IF(AND(TD!A3C$6,TD!$U3=1),$B10,0)
The absolute references allow you to copy this formula through U1009. The weighted error for each possible decision stump may then be calculated in row 7. For cell C7 the calculation of the weighted error is:
=SUM(C10:C1009)
Copy this across row 7 to get the weighted error of each decision stump (see Figure 7.25).
Figure 7.25 The weighted error calculation for each stump
Label cell W1 as the Winning Error, and in X1, find the minimum of the weighted error values:
=MIN(C7:U7)
Just as in the bagging section, in X2 combine the INDEX and MATCH formulas to grab the feature index of the winning stump:
=INDEX(C1:U1,0,MATCH(X1,C7:U7,0))
And in X3, you can likewise grab the value associated with pregnancy for the stump using INDEX and MATCH:
=INDEX(C6:U6,0,MATCH(X1,C7:U7,0))
This gives the sheet shown in Figure 7.26. Starting with equal weights for each data point, feature index 5 with a value of 0 indicating pregnancy is chosen as the top stump. Flipping back to the TD tab, you can see that this is the Birth Control feature.
Figure 7.26 The first winning boosted stump
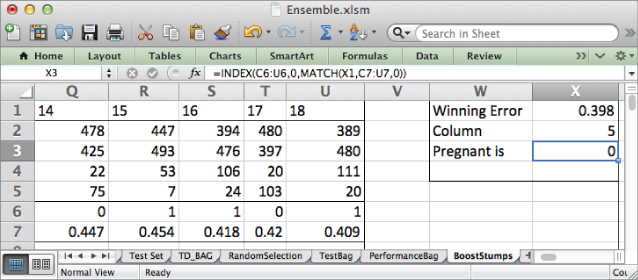
Boosting works by giving weight to training rows that were misclassified by previous stumps. Stumps at the beginning of the boosting process are then more generally effective, while the stumps at the end of the training process are more specialized—the weights have been altered to concentrate on a few annoying points in the training data.
These stumps with specialized weights help fit the model to the strange points in the dataset. However in doing so, their weighted error will be larger than that of the initial stumps in the boosting process. As their weighted error rises, the overall improvement they contribute to the model falls. In boosting, this relationship is quantified with a value called alpha:
alpha = 0.5 * ln((1 – total weighted error for the stump)/total weighted error for the stump)
As the total weighted error of a stump climbs, the fraction inside the natural log function grows smaller and closer to 1. Since the natural log of 1 is 0, the alpha value gets tinier and tinier. Take a look at it in the context of the sheet.
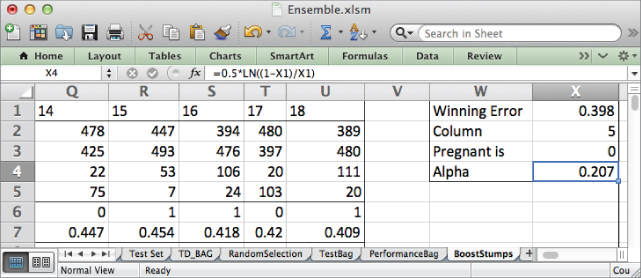
Label cell W4 as Alpha and in X4 send the weighted error from call X1 through the alpha calculation:
=0.5*LN((1-X1)/X1)
For this first stump, you end up with an alpha value of 0.207 (see Figure 7.27).
Figure 7.27 Alpha value for the first boosting iteration
How exactly are these alpha values used? In bagging, each stump gave a 0/1 vote when predicting. When it comes time to predict with your boosted stumps, each classifier will instead give alpha if it thinks the row is pregnant and –alpha if not. So for this first stump, when used on the test set, it would give 0.207 points to any customer who had not bought birth control and -0.207 points to any customer who had. The final prediction of the ensemble model is the sum of all these positive and negative alpha values.
As you'll see later on, to determine the overall pregnancy prediction coming from the model, a cutoff is set for the sum of the individual stump scores. Since each stump returns either a positive or negative alpha value for its contribution to the prediction, it is customary to use 0 as the classification threshold for pregnancy, however this can be tuned to suit your precision needs.
Now that you've completed one stump, it's time to reweight the training data. And to do that, you need to know which rows of data this stump gets right and which rows it gets wrong.
So in column V label V9 as Wrong. In V10, you can use the OFFSET formula in combination with the winning stump's column index (cell X2) to look up the weighted error for the training row. If the error is nonzero, then the stump is incorrect for that row, and Wrong is set to 1:
=IF(OFFSET($C10,0,$X$2)>0,1,0)
This formula can be copied down to all training rows (note the absolute references).
Now, the original weights for this stump are in column B. To adjust the weights according to which rows are set to 1 in the Wrong column, boosting multiplies the original weight times exp(alpha * Wrong) (where exp is the exponential function you encountered when doing logistic regression in Chapter 6).
If the value in the Wrong column is 0, then exp(alpha * Wrong) becomes 1, and the weight stays put.
If Wrong is set to 1, then exp(alpha * Wrong) is a value larger than 1, so the entire weight is scaled up. Label column W as Scale by Alpha, and in W10, you can calculate this new weight as:
=$B10*EXP($V10*$X$4)
Copy this down through the dataset.
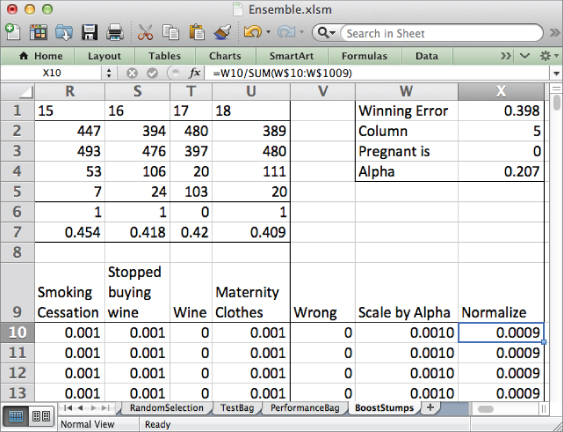
Unfortunately, these new weights don't sum up to one like your old weights. They need to be normalized (adjusted so that they sum to one). So label X9 as Normalize and in X10, divide the new, scaled weight by the sum of all the new weights:
=W10/SUM(W$10:W$1009)
This ensures that your new weights sum to one. Copy the formula down. This gives the sheet shown in Figure 7.28.
Figure 7.28 The new weight calculation
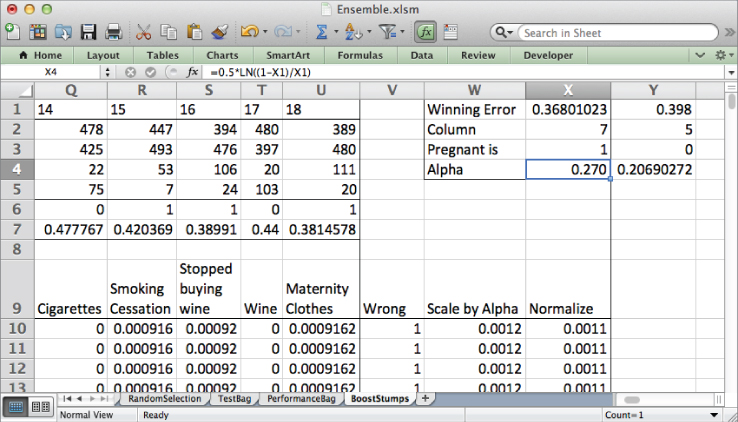
Now you're ready to build a second stump. First, copy the winning stump data from the previous iteration over from X1:X4 to Y1:Y4.
Next, copy the new weight values from column X over to column B. The entire sheet will update to select the stump that's best for the new set of weights. As shown in Figure 7.29, the second winning stump is index 7 (Folic Acid) where a 1 indicates pregnancy.
Figure 7.29 The second stump
You can train 200 of these stumps in much the same way as you did in the bagging process. Simply record a macro that inserts a new column Y, copies the values from X1:X4 into Y1:Y4, and pastes the weights over from column X to column B.
After 200 iterations, your weighted error rate will have climbed very near to 0.5 while your alpha value will have fallen to 0.005 (see Figure 7.30). Consider that your first stump had an alpha value of 0.2. That means that these final stumps are 40 times less powerful in the voting process than your first stump.
Figure 7.30 The 200th stump

That's it! You've now trained an entire boosted decision stumps model. You can compare it to the bagged model by looking at its performance metrics. To make that happen, you must first make predictions using the model on the test set data.
First make a copy of the Test Set called TestBoost and insert four blank rows at the top of it to make room for your winning decision stumps. Beginning in column W on the TestBoost tab, paste your stumps (all 200 in my case) at the top of the sheet. This gives the sheet shown in Figure 7.31.
Figure 7.31 Decision stumps pasted to TestBoost
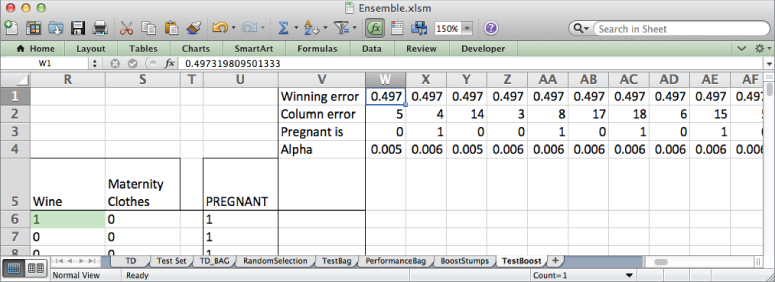
In W6, you can then evaluate the first stump on the first row of test data using OFFSET just as you did with the bagged model. Except this time, a pregnancy prediction returns the stump's alpha value (cell W4) and a non-pregnancy prediction returns –alpha:
=IF(OFFSET($A6,0,W$2)=W$3,W$4,-W$4)
Copy this formula across to all the stumps and down through all the test rows (see Figure 7.32). To make a prediction for a row, you sum these values across all its individual stump predictions.
Figure 7.32 Predictions on each row of test data from each stump
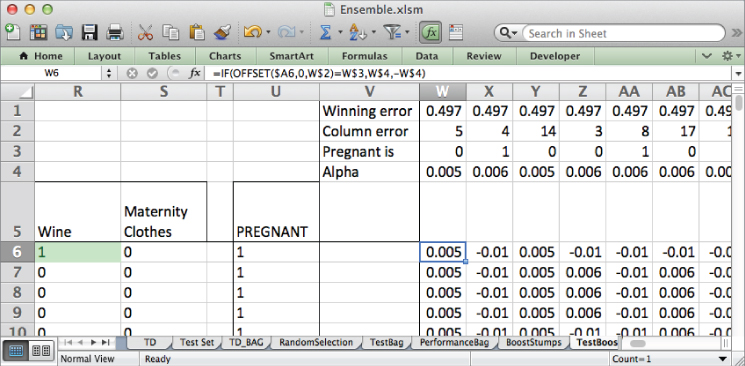
Label V5 as Score. The score then for V6 is just the sum of the predictions to the right:
=SUM(W6:HN6)
Copy this sum down. You get the sheet shown in Figure 7.33. A score in column V above 0 means that more alpha-weighted predictions went in the pregnant direction than in the not pregnant direction (see Figure 7.33).
Figure 7.33 Final predictions from the boosted model
To measure the performance of the boosted model on the test set, simply create a copy of the PerformanceBag tab called PerformanceBoost, point the formulas at column V on the TestBoost tab, and set the cutoff values to range from the minimum score to the maximum score produced by the boosted model. In my case, I incremented the cutoff values by 0.25 between a minimum prediction score of -8 and a maximum of 4.5. This gives the performance tab shown in Figure 7.34.
Figure 7.34 The performance metrics for boosted stumps
With this model, you can see that a score cutoff of 0 produces a true positive rate 85 percent with only a 27 percent false positive rate. Not bad for 200 stupid stumps.
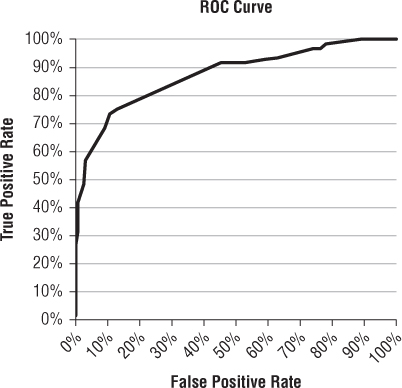
Add the boosted model's ROC curve to the bagged model's ROC curve to compare the two just as you did in Chapter 6. As seen in Figure 7.35, at 200 stumps each, the boosted model outperforms the bagged model for many points on the graph.
Figure 7.35 The ROC curves for the boosted and bagged models
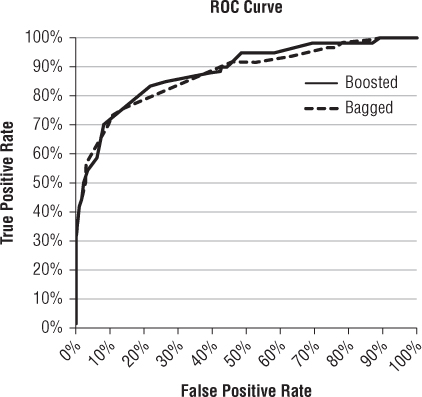
In general, boosting requires fewer trees than bagging to produce a good model. It's not as popular in practice as bagging, because there is a slightly higher risk of overfitting the data. Since each reweighting of the training data is based on the misclassified points in the previous iteration, you can end up in a situation where you're training classifiers to be overly-sensitive to a few noisy points in the data.
Also, the iterative reweighting of the data means that boosting, unlike bagging, cannot be parallelized across multiple computers or CPU cores.
That said, in a neck and neck contest between a well fit boosted model and a well fit bagged model, it's hard for the bagged model to win.
You've just seen how a bunch of simple models can be combined via bagging or boosting to form an ensemble model. These approaches were unheard of until about the mid-1990s, but today, they stand as two of the most popular modeling techniques used in business.
And you can boost or bag any model that you want to use as a weak learner. These models don't have to be decision stumps or trees. For example, there's been a lot of talk recently about boosting naïve Bayes models like the one you encountered in Chapter 3.
In Chapter 10, you'll implement some of what you've encountered in this chapter using the R programming language.
If you'd like to learn more about these algorithms, I'd recommend reading about them in The Elements of Statistical Learning by Trevor Hastie, Robert Tibshirani, and Jerome Friedman (Springer, 2009).