Average Hedge Funds and their Evaluation¹

Analyzing those who regularly beat a vanilla buy and hold strategy

We know that on average the typical mutual fund does not beat the market. The evidence is that professional managers all over the world have a hard time beating the market averages. In a given year, only about 25% to 40% of managers actually beat a buy-and-hold strategy of holding the index. Over longer periods, say 5-10 years, the percentage is even lower. There are a number of reasons for this.

•The market averages stay fully invested at all times, never missing market moves nor paying commissions for stock changes and market timing.

•When funds get behind the index, they often make hasty moves to try to catch up and, more often than not, this puts them further behind.

•Portfolio managers have a tendency to window dress at reporting times, adding to turnover and commissions.

•Since the managers collectively more or less are the market (with individual investors forming less and less of the market each year) the indices, on average, beat half of the fund managers. Then with commissions, fees, and these other reasons, only 25% to 40% typically beat the market averages (which does quite well with a lot less work).

•The fund managers take fees; the averages work for free.

•The fund managers' goals may get in the way of the fund's best interests which creates an agency problem.

•Portfolio managers tend to follow each other's moves. They tend to move the market which gains the full amount, and they can easily be a little behind.

We have the following four reasons the high commissions of active trading often lead to poorer performance than the market indices.

(1)commissions are higher in active portfolios because the turnover is greater.

(2)the bid-ask spreads are larger for many smaller international securities that an active manager would buy

(3)exchange taxes can be as large as 1% on both buys and sells

(4)active managers usually hold a small number of large positions so they have market impact on getting in and out.

Index funds have grown and grown. Dimension Fund Advisors formed by University of Chicago Professor Eugene Fama's students David Booth and Rex Sinquefield manage over $250 billion and others such as Barclays in San Francisco manage over $100 billion. This is done with low fees in an efficient manner. The indices for these passive funds have grown to include small cap, foreign investments and a variety of exchange traded funds as well as the traditional market index, the S&P500. Despite very low fees, profits are large. Booth was able to give the University of Chicago Business School $300 million and it is now the Booth Graduate School of Business.

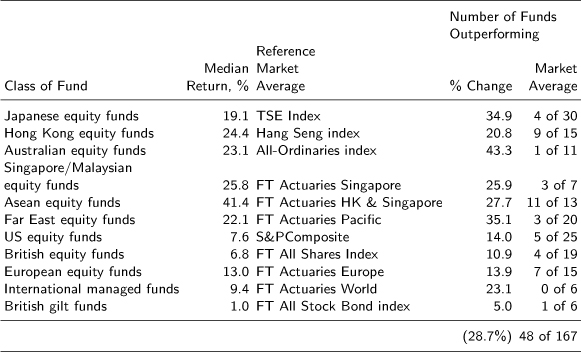
Table 4.1 shows results for 1988 for 167 funds based in Hong Kong with investments in various parts of the world. Only 48, or 28.7%, actually beat the benchmark indices. ASEAN equity funds did do well, averaging 41.4% returns versus the market's 27.7%, and 11 of the 13 funds beat this measure. But Japanese equity funds did not fare so well. Indeed only 4 out of 30 funds beat the TSE index of 34.9% and their average return was 19.1%, more than 15 points below the Topix.

Thus the efficient market proponents have one of their greatest success, namely that, for most of the time, most investors will do quite well by simply investing in index funds. Indeed, even the great investor David Swensen, who runs the Yale endowment discussed in Chapter 11, suggests that most people are well served with tax efficient exchange traded funds, see Swensen (2000).

Indeed from February 28, 2003 to July 20, 2007, the S&P500 has gained 82%. Whoops, that's in the declining US dollar. Meanwhile, gold in US dollars is up 82%, Brazil up 92%, the euro has risen from 0.87 in January 2002 to 1.38 in late July 2007, the British pound at 2.05 is at a decades high level and even the Canadian dollar, stuck at 63-64 cents for years until 2002 is at 95 cents. Even the Kiwi and Aussie dollars are flying with the Aussie up from 78 to 85 in just the last few months. The Chinese and Japanese currencies have been held back but that's given each of them over $1 trillion in foreign reserves. The Chinese stock market is the highest gainer, over 100% this past year in a strong currency.

Table 4.1: Sector Median Returns of Hong Kong Based Funds Compared with Market Average, January 1 to November 30, 1988. Source: Ziemba and Schwartz (1991)

Forsyth (2007) argues that these rises are simply due to global liquidity. But this situation is fast changing. Cheap funds for investments like the US sub-prime mortgages repackaged into various erroneously labeled AAA instruments and private equity levered buyouts is drying up especially seen in the implosion of the subprime instruments.

In the short term the Chinese investment in Blackstone which was purchased at a 4.5% discount from the IPO (about $31 per share) is underperforming T-bonds with the stock at 24. This Chinese investment is relationship based as well as an investment per se.² It remains to be seen if the Chinese invest better than the Japanese did; see Ziemba and Schwartz (1992) for a discussion and a listing of Japanese trophy purchases that lost money. In trading one must always be ready for mini-storms at any time. And a new one has appeared in late July 2007 with the S&P500 falling over 50 points in two days and the VIX volatility index rising to over 24% very high for the year which saw a low of 9.39% but well below the 44% in 1998.

This chapter focuses on the average hedge funds and then on one of the current great funds, Renaissance's Medallion. For the average funds I look at the effects of incentives and the general partners' stake in the fund while Medallion, provides the opportunity to see how Ziemba's (2005) downside symmetric Sharpe ratio is a much better way to evaluate superior investors than the ordinary Sharpe ratio.

I discuss some aspects of hedge funds, specifically the very important risk control point that risk behavior is greatly improved in situations where the decision maker (eg, manager of the fund) holds (invests) a substantial portion of their own money. That is developed in a hedge fund management model that Roy Kouwen- berg and I developed where the effect of incentive fees on investment behavior can be studied.

Kouwenberg and Ziemba (2007) analyse the effect of incentive fees on risk taking in a continuous-time framework, taking management fees and the manager's own stake in the fund into account. They do not use a standard normative utility function like HARA for the preferences of the fund manager. Rather they use the behavioural setting of prospect theory - a framework for decision-making under uncertainty developed by Kahneman and Tversky (1979). This utility is based on actual human behaviour observed in experiments. Siegmann and Lucas (2002) argue that loss aversion, an important aspect of prospect theory, can explain the non-normal return distributions of hedge funds. Kouwenberg and Ziemba investigate how hedge fund managers driven by these preferences react to incentive fees. They also derive an expression for the value of the manager's incentive fee, as in Goetzmann, Ingersoll and Ross (2003). This call option on other people's money can be worth more than 17% of the invested value. Kouwenberg and Ziemba present a continuous time theoretical study of how incentives affect hedge fund risk and returns and an empirical study of the performance of a large group of operating hedge funds. Most hedge fund managers receive a flat fee plus a share of the returns above a benchmark. They investigate how these features of hedge fund fees affect risk taking by the fund manager in the behavioural framework of prospect theory. Their main conclusions are:

(1)In the theoretical study:

(a)the performance related component encourages funds managers to take excessive risk.

(b)However, risk taking due to incentive fees is greatly reduced if a substantial amount of the manager's own money (30%+) is in the fund. When the manager has 30%+ in the fund, the call option on other people's money drops dramatically from 18% to very little.

(2)In the empirical study (2078 hedge funds and 536 funds of funds; January 1995 - November 2000, Zurich hedge fund universe):

(a)Average returns though, both absolute and risk-adjusted, are significantly lower in the presence of incentive fees.

(b)Even after adjusting for style differences, the average hedge fund does not make back their fees, which average 2+20.

(c)Fund of funds have better performance than individual funds

The management fee covers expenses and provides business income. These fees should moderate risk taking, as negative investment returns reduce the future stream of income from management fees. Most fund managers invest their own money in the fund. This ‘eating your own cooking’, helps to realign the motivation of the fund manager with the objectives of the other investors in the fund. The fact that hedge fund managers typically risk both their career and their own money while managing a fund is a positive sign to outside investors. The personal involvement of the manager, combined with a good and verifiable track record, could explain why outside investors are willing to invest their money in hedge funds, even though investors typically receive very limited information about hedge fund investment strategies and also possibly face poor liquidity due to lock-up periods in some funds. The loss averse hedge fund managers increase risk taking in response to the incentive fees, regardless of whether the fund value is above or below the benchmark. One would expect that the hedge fund manager's own stake in the fund is an essential factor influencing the relationship between incentives and risk taking, and they find that the model predicts this.

The utility function is

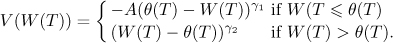
•The fund manager has a threshold θ(T) > 0 for separating gains and losses.

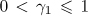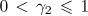•The parameters and determine the curvature of the value function over losses and gains respectively.

•The parameter A > 0 is the level of loss aversion of the hedge fund manager.

•In prospect theory it is assumed that losses are more important than gains, that is A > 1; so the pain of a loss exceeds the positive feeling associated with an equivalent gain.

The continuous time model and its mathematical analysis are discussed in Kouwenberg and Ziemba (2007). The following figures and tables present the main results.

To analyze the effect of incentive fees on the investment strategy of the fund manager, they used the fact that the implicit level of loss aversion A of the fund manager decreases as a function of the incentive fee level as shown in Figure 4.1 for three different levels (5%, 20% and 50%) of the managers stake in the fund.

As the incentive fee increases, the implicit level of loss aversion of the fund manager decreases, indicating that the manager should optimally care less about losses and more about gains due to the convex compensation structure. The negative impact of incentive fees on implicit loss aversion is mitigated to some extent if the manager owns a substantial part the fund.

The initial fund value is 1, the threshold for the incentive fee is 1, the management fee is 1% and the manager's own stake in the fund is 20%. Given these parameters, Figure 4.2 shows the optimal weight of risky assets in the fund, as a function of fund value at time t = 0.5. Each line in Figure 4.2 represents a different level of incentive fee, ranging from 0% to 30%. The fund manager takes more risk in responoe to an infreaeing incentive fee. The increase in risk is more pronouncvd when fund value drops below the benchmark. Due to the structure of the value function oi prospect theory, a fund manager without an incentive fee will inerease risk; at low fund values as well; incentive fees amplify this behauiour.

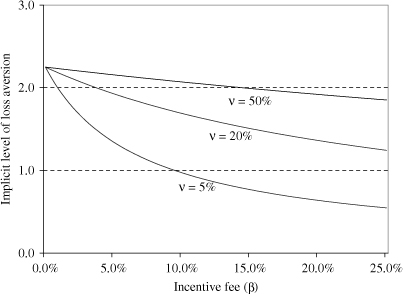
Fig. 4.1Implicit level of loss a'version as a function of incentive fee with fixed fee of a==1%, lines for different levele of the managee's stake in the fund (v). Source: Kouwenberg and Ziemba (2007)

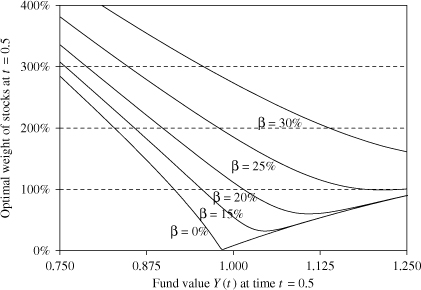
Fig. 4.2 Optimal weight of stocksas a function of fund value, manager's stake in the fund v=20%, lines for different levels of the incentive fee (,8). Source: Kouwenberg and Ziemba (2007)

Figure 4.3 shows the effect on the optimal investment strategy of changing the manager's ewn stake in the funi given an incentive fee of 20%. It demonstrates that an increase of the manager's share in the fund can completely change risk taking. With a stake of 10% or less, the manager behaves extremely risk seeking as a result of the incentive fee. However, with a stake of 30% or more, the investment strategy is similar to the base case of 100%% ownership (without an incentive fee).

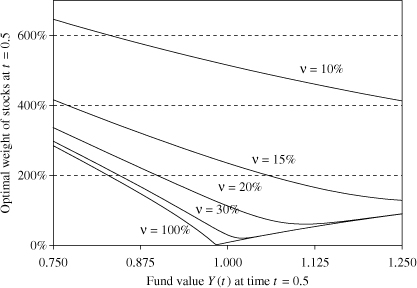
Fig. 4.3 Optimal weight of stocks as a function of fund value, incentive fee of β = 20% for different levels of the managers stake in the fund (v). Source: Kouwenberg and Ziemba (2007)

Figurf 4.4 shows the manager's initial waight of aisky assets aa a function of the incentive fee. The different lines represent different levels of ^ehe manager's own stake in tnhe fund. Again higher incentive fees lead to increased risk taking; the increase in risk taking is more drastic when the managers own stake in the fund is low .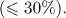

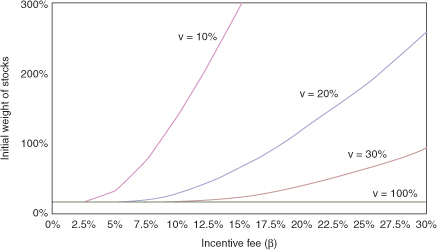
Fig. 4.4 Initial weight of stocks as a function of the incentive fee for different levels of the managers stake in the fund (v)

Figure 4.5 plots the value of a 20% incentive fee as a function of the manager's stake in the fund, using the same set of parameters as above. The value of the 20% incentive fee ranges from nearly zero to 17% of the initial fund value, depending on the manager's own stake in the fund. If the manager's stake in the fund is 100%, the manager does not care about the incentive fee and manages the fund conservatively since it is a personal account. However, as the manager's stake in the fund goes to zero, the manager starts to increase the volatility of the investment strategy in order to reap more profits from the incentive fee contract.

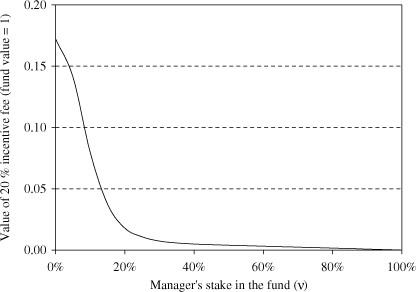
Fig. 4.5 Option value of 20% incentive fee s a function of the incentive fee for different levels of the managers stake in the fund (v). Source: Kouwenberg and Ziemba (2007)

Figure 4.6 shows the optimal volatility of the fund returns Y (T)/Y(0) as a function of the manager's stake in the fund, given the incentive fee of 20%. The fund manager greatly invreases the fund's return volatility as the manager's own stake in the fund decreases, to maximize the expected payoff of the incentive fee.

The increase of the value of the incentive fee, due to this change in investment behaviour, is as much 2125% in this example; essentially from to 17% of initial fund value

The theory thus suggests that it is best to invest in hedge funds where the fund managers eat their own cooking and invest preferably 30%+ of the fund's assets from their own resources. As I have repeatedly argued, the recipe for hedge fund disasters is: to overbet and not diversify in all the possible scenarios.

A super important point here relevant to the 2007-2009 financial morket meltdown that was teiggered by eiskt subprime mortgages is that a rule that banks and other institutions keep 30%+ of their mortgages would lower their risk as they would take more care in granting mortgages. Canadian banks typically hold 100% of their mortgages. This leads to carefully considering the ability of the borrowers to service their mortgages and their default rates were very low and house prices are at an all time high. This also extends to other instruments in the current crisis, relates to some of the regulations that have been suggested, and would probably have avoided the GS problem as well!

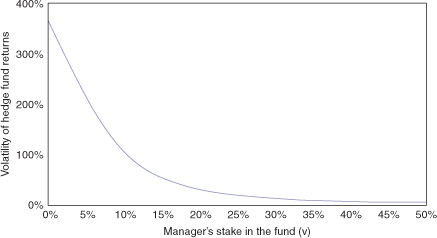
Fig. 4.6 Optimal volatility of fund returns with incentive fee of 20% as a function of the incentive fee for different levels of the managers stake in the fund (v)

As we see from this model, the hedge fund manager has a great incentive to increase risk if they do not have much of their own money in the fund and that can easily lead to large losses. An especially dangerous situation is the multi-billion dollar fund with a hot fund manager who has huge bets in a narrow area with little in the fund getting high fees stored away. Since the penalties for a blowup are very low, this manager's incentive is to shoot for the fences and if fired after a blowup, walk away with the previous fees and get another hedge fund job. Examples include Victor Niederhoffer, John Merriwether, Brian Hunter and others. Some examples are discussed in Chapter 26.

¹ Edited from Wilmott, September 2007.

²Their next move seems to be into Barclays which is bidding on ABM-AMBRO but lost out to RBS which lost billions on this deal by over paying for ABM-AMBRO.