CHAPTER 11
PORTFOLIO CONCEPTS
1. INTRODUCTION
No aspect of quantitative investment analysis is as widely studied or as vigorously debated as portfolio theory. Issues that portfolio managers have studied during the last 50 years include the following:
• What characteristics of a portfolio are important, and how may we quantify them?
• How do we model risk?
• If we could know the distribution of asset returns, how would we select an optimal portfolio?
• What is the optimal way to combine risky and risk-free assets in a portfolio?
• What are the limitations of using historical return data to predict a portfolio’s future characteristics?
• What risk factors should we consider in addition to market risk?
In this chapter, we present key quantitative methods to support the management of portfolios. In Section 2, we focus on mean – variance analysis and related models and issues. Then in Section 3, we address some of the problems encountered using mean – variance analysis and how we can respond to them. We introduce a single-factor model, the market model, which explains the return on assets in terms of a single variable, a market index. In Section 4, we present models that explain the returns on assets in terms of multiple factors, and we illustrate some important applications of these models in current practice.
2. MEAN – VARIANCE ANALYSIS
When does portfolio diversification reduce risk? Are there some portfolios that all risk-averse investors would avoid? These are some of the questions that Harry Markowitz addressed in the research for which he shared the 1990 Nobel Prize in Economics.
Mean – variance portfolio theory, the oldest and perhaps most accepted part of modern portfolio theory, provides the theoretical foundation for examining the roles of risk and return in portfolio selection. In this section, we describe Markowitz’s theory, illustrate the principles of portfolio diversification with several examples, and discuss several important issues in implementation.
Mean – variance portfolio theory is based on the idea that the value of investment opportunities can be meaningfully measured in terms of mean return and variance of return. Markowitz called this approach to portfolio formation
mean – variance analysis. Mean – variance analysis is based on the following assumptions:
1. All investors are risk averse; they prefer less risk to more for the same level of expected return.
374 2. Expected returns for all assets are known.
3. The variances and covariances of all asset returns are known.
4. Investors need only know the expected returns, variances, and covariances of returns to determine optimal portfolios. They can ignore skewness, kurtosis, and other attributes of a distribution.
375 5. There are no transaction costs or taxes.
Note that the first assumption does not mean that all investors have the same tolerance for risk. Investors differ in the level of risk they are willing to accept; however, risk-averse investors prefer as little risk as possible for a given level of expected return. In practice, expected returns and variances and covariances of returns for assets are not known but rather estimated. The estimation of those quantities may be a source of mistakes in decision-making when we use mean – variance analysis.
The fourth assumption is a key one, as it says that we may rely on certain summary measures of assets’ return distributions—expected returns, variances, and covariances—to determine which combinations of assets make an optimal portfolio.
2.1. The Minimum-Variance Frontier and Related Concepts
An investor’s objective in using a mean – variance approach to portfolio selection is to choose an efficient portfolio. An efficient portfolio is one offering the highest expected return for a given level of risk as measured by variance or standard deviation of return. Thus if an investor quantifies her tolerance for risk using standard deviation, she seeks the portfolio that she expects will deliver the greatest return for the standard deviation of return consistent with her risk tolerance. We begin the exploration of portfolio selection by forming a portfolio from just two asset classes, government bonds and large-cap stocks.
Table 11-1 shows the assumptions we make about the expected returns of the two assets, along with the standard deviation of return for the two assets and the correlation between their returns.
To begin the process of finding an efficient portfolio, we must identify the portfolios that have minimum variance for each given level of expected return. Such portfolios are called minimum-variance portfolios. As we shall see, the set of efficient portfolios is a subset of the set of minimum variance portfolios.
We see from
Table 11-1 that the standard deviation of the return to large-cap stocks (Asset 1) is 15 percent, the standard deviation of the return to government bonds (Asset 2) is 10 percent, and the correlation between the two asset returns is 0.5. Therefore, we can compute the variance of a portfolio’s returns as a function of the fraction of the portfolio invested in large-cap stocks (
w1) and the fraction of the portfolio invested in government bonds (
w2). Because the portfolio contains only these two assets, we have the relationship
w1 +
w2 = 1. When the portfolio is 100 percent invested in Asset 1,
w1 is 1.0 and
w2 is 0; and when
w2 is 1.0, then
w1 is 0 and the portfolio is 100 percent invested in Asset 2. Also, when
w1 is 1.0, we know that our portfolio’s expected return and variance of return are those of Asset 1. Conversely, when
w2 is 1.0, the portfolio’s expected return and variance are those of Asset 2. In this case, the portfolio’s maximum expected return is 15 percent if 100 percent of the portfolio is invested in large-cap stocks; its minimum expected return is 5 percent if 100 percent of the portfolio is invested in government bonds.
TABLE 11-1 Assumed Expected Returns, Variances, and Correlation: Two-Asset Case
| Asset 1 Large-Cap Stocks | Asset 2 Government Bonds |
|---|
| Expected return | 15% | 5% |
| Variance | 225 | 100 |
| Standard deviation | 15% | 10% |
| Correlation | 0.5 | |
Before we can determine risk and return for all portfolios composed of large-cap stocks and government bonds, we must know how the expected return, variance, and standard deviation of the return for any two-asset portfolio depend on the expected returns of the two assets, their variances, and the correlation between the two assets’ returns.
For any portfolio composed of two assets, the expected return to the portfolio,
E(
Rp), is
E(Rp) = w1E(R1) + w2E(R2)
where
E(R1 ) = the expected return on Asset 1
E(R2) = the expected return on Asset 2
The portfolio variance of return is
where
σ1 = the standard deviation of return on Asset 1
σ2 = the standard deviation of return on Asset 2
ρ1,2 = the correlation between the two assets’ returns
and Cov(
R1,
R2) = ρ
1,2σ
1σ
2 is the covariance between the two returns, recalling the definition of correlation as the covariance divided by the individual standard deviations. The portfolio standard deviation of return is
In this case, the expected return to the portfolio is
E(
Rp) =
w1(0.15) +
w2(0.05), and the portfolio variance is

.
Given our assumptions about the expected returns, variances, and return correlation for the two assets, we can determine both the variance and the expected return of the portfolio as a function of the proportion of assets invested in large-cap stocks and government bonds.
Table 11-2 shows the portfolio expected return, variance, and standard deviation as the weights on large-cap stocks rise from 0 to 1.0.
TABLE 11-2 Relation Between Expected Return and Risk for a Portfolio of Stocks and Bonds
As
Table 11-2 shows, when the weight on large-cap stocks is 0.1, the expected portfolio return is 6 percent and the portfolio variance is 96.75.
376 That portfolio has a higher expected return and lower variance than a portfolio with a weight of 0 on stocks—that is, a portfolio fully invested in government bonds. This improvement in risk-return characteristics illustrates the power of diversification: Because the returns to large-cap stocks are not perfectly correlated with the returns to government bonds (they do not have a correlation of 1), by putting some of the portfolio into large-cap stocks, we increase the expected return and reduce the variance of return. Furthermore, there is no cost to improving the risk-return characteristics of the portfolio in this way.
Figure 11-1 graphs the possible combinations of risk and return for a portfolio composed of government bonds and large-cap stocks.
Figure 11-1 plots the expected portfolio return on the
y-axis and the portfolio variance on the
x-axis.
The two-asset case is special because all two-asset portfolios plot on the curve illustrated (there is a unique combination of two assets that provides a given level of expected return). This is the
portfolio possibilities curve—a curve plotting the expected return and risk of the portfolios that can be formed using two assets. We can also call the curve in
Figure 11-1 the
minimum-variance frontier because it shows the minimum variance that can be achieved for a given level of expected return. The minimum-variance frontier is a more useful concept than the portfolio possibilities curve because it also applies to portfolios with more than two assets. In the general case of more than two assets, any portfolios plotting on an imaginary horizontal line at any expected return level have the same expected return, and as we move left on that line, we have less variance of return. The attainable portfolio farthest to the left on such a line is the minimum-variance portfolio for that level of expected return and one point on the minimum-variance frontier. With three or more assets, the minimum-variance frontier is a true frontier: It is the border of a region representing all combinations of expected return and risk that are possible (the border of the feasible region). The region results from the fact that with three or more assets, an unlimited number of portfolios can provide a given level of expected return.
377 In the case of three or more assets, if we move to the right from a point on the minimum-variance frontier, we reach another portfolio but one with more risk.
FIGURE 11-1 Minimum-Variance Frontier: Large Cap Stocks and Government Bonds
From
Figure 11-1, note that the variance of the global minimum-variance portfolio (the one with the smallest variance) appears to be close to 96.43 (Point A) when the expected return of the portfolio is 6.43. This global minimum-variance portfolio has 14.3 percent of assets in large-cap stocks and 85.7 percent of assets in government bonds. Given these assumed returns, standard deviations, and correlation, a portfolio manager should not choose a portfolio with less than 14.3 percent of assets in large-cap stocks because any such portfolio will have both a higher variance and a lower expected return than the global minimum-variance portfolio. All of the points on the minimum-variance frontier below Point A are inferior to the global minimum-variance portfolio, and they should be avoided.
FIGURE 11-2 Minimum-Variance Frontier: Large-Cap Stocks and Government Bonds

Financial economists often say that portfolios located below the global minimum-variance portfolio (Point A in
Figure 11-1) are dominated by others that have the same variances but higher expected returns. Because these dominated portfolios use risk inefficiently, they are inefficient portfolios. The portion of the minimum-variance frontier beginning with the global minimum-variance portfolio and continuing above it is called the
efficient frontier. Portfolios lying on the efficient frontier offer the maximum expected return for their level of variance of return. Efficient portfolios use risk efficiently: Investors making portfolio choices in terms of mean return and variance of return can restrict their selections to portfolios lying on the efficient frontier. This reduction in the number of portfolios to be considered simplifies the selection process. If an investor can quantify his risk tolerance in terms of variance or standard deviation of return, the efficient portfolio for that level of variance or standard deviation will represent the optimal mean-variance choice.
Because standard deviation is easier to interpret than variance, investors often plot the expected return against standard deviation rather than variance.
378 Figure 11-2 plots the expected portfolio return for this example on the
y-axis and the portfolio standard deviation of return on the
x-axis.
379 The curve graphed is still called the minimum variance frontier.
Example 11-1 illustrates the process of determining a historical minimum-variance frontier.
EXAMPLE 11-1 A Two-Asset Minimum-Variance Frontier Using Historical U.S. Return Data
Susan Fitzsimmons has decided to invest her retirement plan assets in a U.S. small-cap equity index fund and a U.S. long-term government bond index fund. Fitzsimmons decides to use mean-variance analysis to help determine the fraction of her funds to invest in each fund. Assuming that expected returns and variances can be estimated accurately using monthly historical returns from 1970 through 2002, she computes the average returns, variances of returns, and correlation of returns for the indexes that the index funds attempt to track.
Table 11-3 shows those historical statistics.
TABLE 11-3 Average Returns and Variances of Returns (Annualized, Based on Monthly Data, January 1970-December 2002)1-3
Source: Ibbotson Associates.
| Asset Class | Average Return | Variance |
|---|
| U.S. small-cap stocks | 14.63% | 491.8 |
| U.S. long-term government bonds | 9.55% | 109.0 |
| Correlation | 0.138 | |
Given these statistics, Fitzsimmons can determine the allocation of the portfolio between the two assets using the expected return and variance. To do so, she must calculate
• the range of possible expected returns for the portfolio (minimum and maximum),
• the proportion of each of the two assets (asset weights) in the minimumvariance portfolio for each possible level of expected return, and
• the variance
380 for each possible level of expected return.
Because U.S. government bonds have a lower expected return than U.S. small-cap stocks, the minimum expected return portfolio has 100 percent weight in U.S. long-term government bonds, 0 percent weight in U.S. small-cap stocks, and an expected return of 9.55 percent. In contrast, the maximum expected return portfolio has 100 percent weight in U.S. small-cap stocks, 0 percent weight in U.S. long-term government bonds, and an expected return of 14.63 percent. Therefore, the range of possible expected portfolio returns is 9.55 percent to 14.63 percent.
Fitzsimmons now determines the asset weights of the two asset classes at different levels of expected return, starting at the minimum expected return of 9.55 percent and concluding at the maximum level of expected return of 14.63 percent. The weights at each level of expected return determine the variance for the portfolio consisting of these two asset classes.
Table 11-4 shows the composition of portfolios for various levels of expected return.
TABLE 11-4 Points on the Minimum-Variance Frontier for U.S. Small-Cap Stocks and U.S. Long-Term Government Bonds
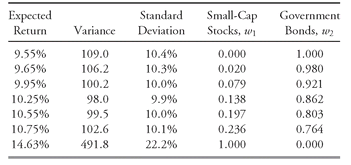
Table 11-4 illustrates what happens to the weights in the individual asset classes as we move from the minimum expected return to the maximum expected return. When the expected return is 9.55 percent, the weight for the long-term government bonds is 100 percent. As we increase the expected return, the weight in long-term government bonds decreases; at the same time, the weight for U.S. small stocks increases. This result makes sense because we know that the maximum expected return of 14.63 percent must have a weight of 100 percent in U.S. small stocks. The weights in
Table 11-4 reflect that property. Note that the global minimum-variance portfolio (which is also the global minimum-standard-deviation portfolio) contains some of both assets. A portfolio consisting only of bonds has more risk and a lower expected return than the global minimum-variance portfolio because diversification can reduce total portfolio risk, as we discuss shortly.
Figure 11-3 illustrates the minimum-variance frontier (in the two-asset-class case, merely a portfolio possibilities curve) over the period 1970 to 2002 by graphing expected return as a function of standard deviation.
FIGURE 11-3 Minimum-Variance Frontier: U.S. Small-Cap Stocks and Government Bonds
If Fitzsimmons quantifies her risk tolerance as a standard deviation of 10 percent, for example, mean-variance analysis suggests that she choose a portfolio with an approximate weighting of 0.20 in small-cap stocks and 0.80 in long-term government bonds. One major caution that we shall discuss later in this chapter is that even small changes in inputs can have a significant effect on the minimum-variance frontier, and the future may obviously be very different from the past. The historical record is only a starting point in developing inputs for calculating the minimum-variance frontier.
381The trade-off between risk and return for a portfolio depends not only on the expected asset returns and variances but also on the correlation of asset returns. Returning to the case of large-cap stocks and government bonds, we assumed that the correlation was 0.5. The risk-return trade-off is quite different for other correlation values.
Figure 11-4 shows the minimum-variance frontiers for portfolios containing large-cap stocks and government bonds for varying weights.
382 The weights go from 100 percent in government bonds and 0 percent in large-cap stocks to 0 percent in government bonds and 100 percent in large-cap stocks, for four different values of the correlation coefficient. The correlations illustrated in
Figure 11-4 are—1, 0, 0.5, and 1.
Figure 11-4 illustrates a number of interesting characteristics about minimum-variance frontiers and diversification:
383 • The endpoints for all of the frontiers are the same. This fact should not be surprising, because at one endpoint all of the assets are in government bonds and at the other endpoint all of the assets are in large-cap stocks. At each endpoint, the expected return and standard deviation are simply the return and standard deviation for the relevant asset (stocks or bonds).
• When the correlation is +1, the minimum-variance frontier is an upward-sloping straight line. If we start at any point on the line, for each one percentage point increase in standard deviation we achieve the same constant increment in expected return. With a correlation of +1, the return (not just the expected return) on one asset is an exact positive linear function of the return on the other asset.
384 Because fluctuations in the returns on the two assets track each other in this way, the returns on one asset cannot dampen or smooth out the fluctuations in the returns on the other asset. For a correlation of + 1, diversification has no potential benefits.
FIGURE 11-4 Minimum-Variance Frontier for Varied Correlations: Large-Cap Stocks and Government Bonds
• When we move from a correlation of +1 to a correlation of 0.5, the minimum-variance frontier bows out to the left, in the direction of smaller standard deviation. With any correlation less than +1, we can achieve any feasible level of expected return with a smaller standard deviation of return than for the +1 correlation case. As we move from a correlation of 0.5 to each smaller value of correlation, the minimum-variance frontier bows out farther to the left.
• The frontiers for correlation of 0.5, 0, and—1 have a negatively sloped part.
385 This means that if we start at the lowest point (100 percent in government bonds) and shift money into stocks until we reach the global minimum-variance portfolio, we can get more expected return with less risk. Therefore, relative to an initial position fully invested in government bonds, there are diversification benefits in each of these correlation cases. A diversification benefit is a reduction in portfolio standard deviation of return through diversification without an accompanying decrease in expected return. Because the minimum-variance frontier bows out further to the left as we lower correlation, we can also conclude that as we lower correlation, holding all other values constant, there are increasingly larger potential benefits to diversification.
• When the correlation is −1, the minimum-variance frontier has two linear segments. The two segments join at the global minimum-variance portfolio, which has a standard deviation of 0. With a correlation of—1, portfolio risk can be reduced to zero, if desired.
• Between the two extreme correlations of +1 and—1, the minimum-variance frontier has a bullet-like shape. Thus the minimum-variance frontier is sometimes called the “bullet.”
• The efficient frontier is the positively sloped part of the minimum-variance frontier. Holding all other values constant, as we lower correlation, the efficient frontier improves in the sense of offering a higher expected return for a given feasible level of standard deviation of return.
In summary, when the correlation between two portfolios is less than +1, diversification offers potential benefits. As we lower the correlation coefficient toward—1, holding other values constant, the potential benefits to diversification increase.
2.2. Extension to the Three-Asset Case
Earlier we considered forming a portfolio composed of two assets: large-cap stocks and government bonds. For investors in our example who want to maximize expected return for a given level of risk (hold an efficient portfolio), the optimal portfolio combination of two assets contains some of each asset, unless the portfolio is placed entirely in stocks.
Now we may ask, would adding another asset to the possible investment choices improve the available trade-offs between risk and return? The answer to this question is very frequently yes. A fundamental economic principle states that one is never worse off for having additional choices. At worst, an investor can ignore the additional choices and be no worse off than initially. Often, however, a new asset permits us to move to a superior minimum-variance frontier. We can illustrate this common result by contrasting the minimum-variance frontier for two assets (here, large-cap stocks and government bonds) with the minimum-variance frontier for three assets (large-cap stocks, government bonds, and small-cap stocks).
In our initial two-asset case shown in
Table 11-1, we assumed expected returns, variances, and correlations for large-cap stocks and government bonds. Now suppose we have an additional investment option, small-cap stocks. Can we achieve a better trade-off between risk and return than when we could choose between only two assets, large-cap stocks and government bonds?
Table 11-5 shows our assumptions about the expected returns of all three assets, along with the standard deviations of the asset returns and their correlations.
TABLE 11-5 Assumed Expected Returns, Variances, and Correlations: Three-Asset Case
Now we can consider the relation between these statistics and the expected return and variance for the portfolio. For any portfolio composed of three assets with portfolio weights
w1,
w2, and
w3, the expected return on the portfolio,
E(
Rp), is
E(Rp) = w1E(R1) + w2E(R2) + w3E(R3)
where
E(R1) = the expected return on Asset 1 (here, large-cap stocks)
E(R2) = the expected return on Asset 2 (government bonds)
E(R3) = the expected return on Asset 3 (small-cap stocks)
The portfolio variance is
where
σ1 = the standard deviation of the return on Asset 1
σ2 = the standard deviation of the return on Asset 2
σ3 = the standard deviation of the return on Asset 3
ρ1,2 = the correlation between returns on Asset 1 and Asset 2
ρ1,3 = the correlation between returns on Asset 1 and Asset 3
ρ2,3 =the correlation between returns on Asset 2 and Asset 3
The portfolio standard deviation is
Given our assumptions, the expected return on the portfolio is
E(Rp) = w1(0.15) + w2(0.05) + w3(0.15)
The portfolio variance is
The portfolio standard deviation is
In this three-asset case, however, determining the optimal combinations of assets is much more difficult than it was in the two-asset example. In the two-asset case, the percentage of assets in large-cap stocks was simply 100 percent minus the percentage of assets in government bonds. But with three assets, we need a method to determine what combination of assets will produce the lowest variance for any particular expected return. At least we know the minimum expected return (the return that would result from putting all assets in government bonds, 5 percent) and the maximum expected return (the return from putting no assets in government bonds, 15 percent). For any level of expected return between the minimum and maximum levels, we must solve for the portfolio weights that will result in the lowest risk for that level of expected return. We use an
optimizer (a specialized computer program or a spreadsheet with this capability) to provide these weights.
386TABLE 11-6 Points on the Minimum-Variance Frontier for the Three-Asset Case
Notice that the new asset, small-cap stocks, has a correlation of less than +1 with both large-cap stocks and bonds, suggesting that small-cap stocks may be useful in diversifying risk.
Table 11-6 shows the portfolio expected return, variance, standard deviation, and portfolio weights for the minimum-variance portfolio as the expected return rises from 5 percent to 15 percent.
As
Table 11-6 shows, the proportion of the portfolio in large-cap stocks and small-cap stocks is the same in all the minimum-variance portfolios. This proportion results from the simplifying assumption in
Table 11-5 that large-cap stocks and small-cap stocks have identical expected returns and standard deviations of return, as well as the same correlation with government bonds. With a different, more realistic combination of returns, variances, and correlations, the minimum-variance portfolios in this example would contain different proportions of the large-cap stocks and small-cap stocks, but we would reach a similar conclusion about the possibility of improving the available risk—return trade-offs.
How does the minimum variance for each level of expected return in the three-asset case compare with the minimum variance for each level of expected return in the two-asset case?
Figure 11-5 shows the comparison.
When 100 percent of the portfolio is invested in government bonds, the minimum-variance portfolio has the same expected return (5 percent) and standard deviation (10 percent) in both cases. For every other level of expected return, however, the minimum-variance portfolio in the three-asset case has a lower standard deviation than the minimum-variance portfolio in the two-asset case for the same expected return. Note also that the efficient frontier with three assets dominates the efficient frontier with two assets (we would choose our optimal portfolio from those on the superior efficient frontier).
From this three-asset example, we can draw two conclusions about the theory of portfolio diversification. First, we generally can improve the risk—return trade-off by expanding the set of assets in which we can invest. Second, the composition of the minimum-variance portfolio for any particular level of expected return depends on the expected returns, the variances and correlations of those returns, and the number of assets.
FIGURE 11-5 Comparing Minimum-Variance Frontiers: Three Assets versus Two Assets
2.3. Determining the Minimum-Variance Frontier for Many Assets
We have shown examples of mean-variance analysis with two and three assets. Typically, however, portfolio managers form optimal portfolios using a larger number of assets. In this section, we show how to determine the minimum-variance frontier for a portfolio composed of many assets.
For a portfolio of
n assets, the expected return on the portfolio is
387 (11-1)
The variance of return on the portfolio is
388 (11-2)
Before determining the optimal portfolio weights, remember that the weights of the individual assets in the portfolio must sum to 1:
To determine the minimum-variance frontier for a set of
n assets, we must first determine the minimum and maximum expected returns possible with the set of assets (these are the minimum,
rmin, and the maximum,
rmax, expected returns for the individual assets). Then we must determine the portfolio weights that will create the minimumvariance portfolio for values of expected return between
rmin and
rmax. In mathematical terms, we must solve the following problem for specified values of
z,
rmin ≤
z ≤
rmax:
subject to
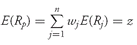
and subject to

This optimization problem says that we solve for the portfolio weights (
w1,
w2,
w3,...,
wn) that minimize the variance of return for a given level of expected return
z, subject to the constraint that the weights sum to 1. The weights define a portfolio, and the portfolio is the minimum-variance portfolio for its level of expected return.
Equation 11-3 shows the simplest case in which the only constraint on portfolio weights is that they sum to 1; this case allows assets to be sold short. A constraint against short sales would require adding a further constraint that
wj ≥ 0. We trace out the minimum-variance frontier by varying the value of expected return from the minimum to the maximum level. For example, we could determine the optimal portfolio weights for a small set of
z values by starting with
z =
rmin, then increasing
z by 10 basis points (0.10 percent) and solving for the optimal portfolio weights until we reach
z =
rmax.
389 We use an optimizer to actually solve the optimization problem. Example 11-2 shows a minimum-variance frontier that results from using historical data for non-U.S. stocks and three U.S. asset classes.
EXAMPLE 11-2 A Minimum-Variance Frontier Using International Historical Return Data
In this example, we examine a historical minimum-variance frontier with four asset classes. The three U.S. asset classes are the S&P 500 Index, U.S. small-cap stocks, and U.S. long-term government bonds. To these we add non-U.S. stocks (MSCI World ex-United States). We estimate the minimum-variance frontier based on historical monthly return data from January 1970 to December 2002.
Table 11-7 presents the mean returns, variances, and correlations of these four assets for the entire sample period.
TABLE 11-7 Mean Annual Returns, Standard Deviations, and Correlation Matrix for Four Asset Classes, January 1970-December 2002
Source: Ibbotson Associates.
Table 11-7 shows that the minimum average historical return from these four asset classes was 9.6 percent a year (bonds) and the maximum average historical return was 14.6 percent (U.S. small-cap stocks). To trace out the minimum-variance frontier, we use the optimization model. The optimization program with a short sales constraint solves for the mean-variance frontier using the following equations:
subject to
E(
Rp)
= w1 E(
R1) +
w2E (
R2) +
w3 E(
R3) +
w4E(
R4) =
z (repeated for specified values of
z, 0.096 ≤
z ≤ 0.146),
w1 +
w2 +
w3 +
w4 = 1, and
wj ≥ 0.
The weights
w1,
w2,
w3, and
w4 represent the four asset classes in the order listed in
Table 11-7. The optimizer chooses the weights (allocations to the four asset classes) that result in the minimum-variance portfolio for each level of average return as we move from the minimum level (
rmin = 9.6 percent) to the maximum level (
rmax = 14.6 percent). In this example,
E(
Rj) is represented by the sample mean return on asset class
j, and the variances and covariances are also sample statistics. Unless we deliberately chose to use these historical data as our forward looking estimates, we would not interpret the results of the optimization as a prediction about the future.
Figure 11-6 shows the minimum-variance frontier for these four asset classes based on the historical means, variances, and covariances from 1970 to 2002. The figure also shows the means and standard deviations of the four asset classes separately.
FIGURE 11-6 Minimum-Variance Frontier for Four Asset Classes, 1970—2002

Although U.S. government bonds lie on the minimum-variance frontier, they are dominated by other asset classes that offer a better mean return for the same level of risk. Note that the points representing S & P 500 and the MSCI World ex-U.S. stocks plotted off and to the right of the minimum-variance frontier. If we move directly to the left from either the S & P 500 or MSCI ex-U.S. stock portfolio, we reach a portfolio on the efficient frontier that has smaller risk without affecting the mean return. If we move directly up from either, we reach a portfolio that has greater mean return with the same level of risk. After the fact, at least, these two portfolios were not efficient for an investor who could invest in all four asset classes. Despite the fact that MSCI World ex-U.S. stocks is itself a very broad index, for example, there were benefits to further diversifying. Of the four asset classes, only U.S. small-cap stocks as the highest-mean-return portfolio plotted on the efficient frontier; in general, the highest-mean-return portfolio appears as an endpoint of the efficient frontier in an optimization with a constraint against short sales, as in this case.
In this section, we showed the process for tracing out a minimum-variance frontier. We also analyzed a frontier generated from actual data. In the next section, we address the relationship between portfolio size and diversification.
2.4. Diversification and Portfolio Size
Earlier, we illustrated the diversification benefits of adding a third asset to a two-asset portfolio. That discussion opened a question of practical interest that we explore in this section: How many different stocks must we hold in order to have a well-diversified portfolio? How does covariance or correlation interact with portfolio size in determining a portfolio’s risk?
We address these questions using the example of an investor who holds an equally weighted portfolio. Suppose we purchase a portfolio of
n stocks and put an equal fraction of the value of the portfolio into each of the stocks (
wi = 1
/n,
i = 1, 2, . . . ,
n). The variance of return is
Suppose we call the average variance of return across all stocks

and the average covariance between all pairs of two stocks
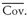
. It is possible to show
390 that
Equation 11-4 simplifies to
As the number of stocks,
n, increases, the contribution of the variance of the individual stocks becomes very small because
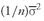
has a limit of 0 as
n becomes large. Also, the contribution of the average covariance across stocks to the portfolio variance stays nonzero because

has a limit of
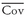
as
n becomes large. Therefore, as the number of assets in the portfolio becomes large, portfolio variance approximately equals average covariance. In large portfolios, average covariance—capturing how assets move together—becomes more important than average individual risk or variance.
In addition to this insight,
Equation 11-5 allows us to gauge the reduction in portfolio variance from the completely undiversified position of holding only one stock. If the portfolio contained only one stock, then of course its variance would be the individual stock’s variance, which is the position of maximum variance.
391 If the portfolio contained a very large number of stocks, the variance of the portfolio would be close to the average covariance of any two of the stocks, known as the position of minimum variance. How large is the difference between these two levels of variance, and how much of the maximum benefit can we obtain with a relatively small number of stocks?
The answers depend on the sizes of the average variance and the average covariance. Because correlation is easier to interpret than covariance, we will work with correlation. Suppose, for simplicity’s sake, that the correlation between the returns for any two stocks is the same and that all stocks have the same standard deviation. Chan, Karceski, and Lakonishok (1999) found that for U.S. NYSE and Amex stocks over the 1968-98 period, the average correlation of small-stock returns was 0.24, the average correlation of large-stock returns was 0.33, and the average correlation of stock returns across the entire sample of stocks was 0.28. Assume that the common correlation is 0.30, which is in the approximate range for the average correlation of U.S. equities for many time periods. The covariance of two random variables is the correlation of those variables multiplied by the standard deviations of the two variables, so

(using our assumption that all stocks have the same standard deviation of returns, denoted σ).
Look back at
Equation 11-5 and replace

with 0.30σ
2:
which provides an example of the more general expression (assuming stocks have the same standard deviation of returns)
(11-6)
If the portfolio contains one stock, the portfolio variance is σ
2. As
n increases, portfolio variance drops rapidly. In our example, if the portfolio contains 15 stocks, the portfolio variance is 0.347σ
2, or only 34.7 percent of the variance of a portfolio with one stock. With 30 stocks, the portfolio variance is 32.3 percent of the variance of a single-stock portfolio. The smallest possible portfolio variance in this case is 30 percent of the variance of a single stock, because

when
n is extremely large. With only 30 stocks, for example, the portfolio variance is only approximately 8 percent larger than minimum possible value (0.323σ
2/0.30σ
2—1 = 0.077), and the variance is 67.7 percent smaller than the variance of a portfolio that contains only one stock.
For a reasonable assumed value of correlation, the previous example shows that a portfolio composed of many stocks has far less total risk than a portfolio composed of only one stock. In this example, we can diversify away 70 percent of an individual stock’s risk by holding many stocks. Furthermore, we may be able to obtain a large part of the risk reduction benefits of diversification with a surprisingly small number of securities.
What if the correlation among stocks is higher than 0.30? Suppose an investor wanted to be sure that his portfolio variance was only 110 percent of the minimum possible portfolio variance of a diversified portfolio. How many stocks would the investor need? If the average correlation among stocks were 0.5, he would need only 10 stocks for the portfolio to have 110 percent of the minimum possible portfolio variance. With a higher correlation, the investor would need fewer stocks to obtain the same percentage of minimum possible portfolio variance. What if the correlation is lower than 0.30? If the correlation among stocks were 0.1, the investor would need 90 stocks in the portfolio to obtain 110 percent of the minimum possible portfolio variance.
One common belief among investors is that almost all of the benefits of diversification can be achieved with a portfolio of only 30 stocks. In fact, Fisher and Lorie (1970) showed that 95 percent of the benefits of diversification among NYSE-traded stocks from 1926 to 1965 were achieved with a portfolio of 32 stocks.
As shown above, the number of stocks needed to achieve a particular diversification gain depends on the average correlation among stock returns: The lower the average correlation, the greater the number of stocks needed. Campbell, Lettau, Malkiel, and Xu (2001) showed that although overall market volatility has not increased since 1963, individual stock returns have been more volatile recently (1986-97) and individual stock returns have been less correlated with each other. Consequently, to achieve the same percentage of the risk-reducing benefits of diversification during the more recent period, more stocks were needed in a portfolio than in the period studied by Fisher and Lorie. Campbell et al. conclude that during the 1963-85 period, “a portfolio of 20 stocks reduced annualized excess standard deviation to about five percent, but in the 1986-1997 subsample, this level of excess standard deviation required almost 50 stocks.”
392EXAMPLE 11-3 Diversification at Berkshire Hathaway
Berkshire Hathaway’s highly successful CEO, Warren Buffett, is one of the harshest critics of modern portfolio theory and diversification. Buffett has said, for example, that “[I]f you are a know-something investor, able to understand business economics, and find 5 to 10 sensibly priced companies that possess important long-term competitive advantages, conventional diversification makes no sense for you. It is apt simply to hurt your results and increase your risk.”
393Does Buffett avoid diversification altogether? Certainly his investment record is phenomenal, but even Buffett engages in diversification to some extent. For example, consider Berkshire Hathaway’s top three investment holdings at the end of 2002.
394
| American Express Company | $ 5.6 billion (32%) |
| The Coca-Cola Company | $ 8.8 billion (51%) |
| The Gillette Company | $ 2.9 billion (17%) |
| Total | $17.3 billion |
How much diversification do these three stocks provide? How much lower is this portfolio’s standard deviation than that of a portfolio consisting only of Coca-Cola stock? To answer these questions, assume that the historical mean returns, return standard deviations, and return correlations of these stocks are the best estimates of the future expected returns, return standard deviations, and return correlations.
Table 11-8 shows these historical statistics, based on monthly return data from 1990 through 2002.
TABLE 11-8 Historical Returns, Variances, and Correlations: Berkshire Hathaway’s Largest Equity Holdings
(Monthly Data, January 1990-December 2002)
Source: FactSet.
Table 11-8 shows that for Coca-Cola’s stock during this period, the mean annual return was 16.1 percent and the annualized standard deviation of the return was 24.7 percent. In contrast, a portfolio consisting of 32 percent American Express stock, 51 percent Coca-Cola stock, and 17 percent Gillette stock had an expected return of 0.32(0.16) + 0.51(0.161) + 0.17(0.176) = 0.163, or 16.3 percent.
The portfolio’s expected standard deviation, based on these weights and the statistics in
Table 11-8, was
or
The standard deviation of a portfolio with these three stocks is only 21.0/24.7 = 85.0 percent of the standard deviation of a portfolio composed exclusively of Coca-Cola stock. Therefore, Berkshire Hathaway actually achieved substantial diversification in the sense of risk reduction, even considering only its top three holdings.
2.5. Portfolio Choice with a Risk-Free Asset
So far, we have considered only portfolios of risky securities, implicitly assuming that investors cannot also invest in a risk-free asset. But investors can hold their own government’s securities such as Treasury bills, which are virtually risk-free in nominal terms over appropriate time horizons. For example, the purchaser of a one-year Treasury bill knows his nominal return if he holds the bill to maturity. What is the trade-off between risk and return when we can invest in a risk-free asset?
A risk-free asset’s standard deviation of return is 0 because the return is certain and there is no risk of default. Suppose, for example, that the return to the risk-free asset is 4 percent a year. If we take the Treasury bill as risk-free, then 4 percent is the actual return, known in advance; it is not an expected return.
395 Because the risk-free asset’s standard deviation of return is 0, the covariance between the return of the risk-free asset and the return of any other asset must also be 0. These observations help us understand how adding a risk-free asset to a portfolio can affect the mean-variance trade-off among assets.
2.5.1. The Capital Allocation Line The capital allocation line (CAL) describes the combinations of expected return and standard deviation of return available to an investor from combining her optimal portfolio of risky assets with the risk-free asset. Thus the CAL describes the expected results of the investor’s decision on how to optimally allocate her capital among risky and risk-free assets.
What graph in mean return-standard deviation space satisfies the definition of the CAL? The CAL must be the line from the risk-free rate of return that is tangent to the efficient frontier of risky assets; of all lines we could extend from the risk-free rate to the efficient frontier of risky assets, the tangent line has the maximum slope and best risk-return tradeoff (“tangent” means touching without intersecting). The tangency portfolio is the investor’s optimal portfolio of risky assets. The investor’s risk tolerance determines which point on the line he or she will choose. Example 11-4 and the ensuing discussion clarify and illustrate these points.
EXAMPLE 11-4 An Investor’s Trade-Off Between Risk and Return with a Risk-Free Asset
Suppose that we want to determine the effect of including a risk-free asset in addition to large-cap stocks and government bonds in our portfolio.
Table 11-9 shows the hypothetical expected returns and correlations for the three asset classes.
TABLE 11-9 Expected Returns, Variances, and Correlations: Three-Asset Case with Risk-Free Asset
Suppose we decide to invest the entire portfolio in the risk-free asset with a return of 4 percent. In this case, the expected return to the portfolio is 4 percent and the expected standard deviation is 0. Now assume that we put the entire portfolio into large-cap stocks. The expected return is now 15 percent, and the standard deviation of the portfolio is 15 percent. What will happen if we divide the portfolio between the risk-free asset and large-cap stocks? If the proportion of assets in large-cap stocks is
w1 and the proportion of assets in the risk-free asset is (1—
w1), then the expected portfolio return is
E(Rp) = w1(0.15) + (1—w1)(0.04)
and the portfolio standard deviation is
Note that both the expected return and the standard deviation of return are linearly related to
w1, the percentage of the portfolio in large-cap stocks.
Figure 11-7 illustrates the trade-off between risk and return for the risk-free asset and large-cap stocks in this example.
FIGURE 11-7 Portfolios of the Risk-Free Asset and Large-Cap Stocks
Now let us consider the trade-off between risk and return for a portfolio containing the risk-free asset and U.S. government bonds. Suppose we decide to put the entire portfolio in the risk-free asset. In this case, the expected return to the portfolio is 4 percent and the expected standard deviation of the portfolio is 0. Now assume that we put the entire portfolio into U.S. government bonds. The expected return is now 5 percent, and the standard deviation of the portfolio is 10 percent. What will happen if we divide the portfolio between the risk-free asset and government bonds? If the proportion of assets in government bonds is
w1 and the proportion of assets in the risk-free asset is (1—
w1), then the expected portfolio return is
E(Rp) = w1 (0.05) + (1—w1)(0.04)
and the portfolio standard deviation is
Note that both the expected return and the standard deviation of return are linearly related to
w1, the percentage of the portfolio in the government bonds.
Figure 11-8 shows the trade-off between risk and return for the risk-free asset and government bonds in this example.
FIGURE 11-8 Portfolios of the Risk-Free Asset and Government Bonds
We have just seen the trade-off between risk and return for two different portfolios: one with the risk-free asset and large-cap stocks, the other with the risk-free asset and government bonds. How do these trade-offs between risk and return compare with the original risk-return trade-off between government bonds and large-cap stocks?
Figure 11-9 illustrates the risk-return trade-off for all three portfolios.
Notice that the line describing portfolios of the risk-free asset and government bonds touches the minimum-variance frontier for bonds and stocks at the point of lowest return on the bond-stock minimum-variance frontier—that is, the point where 100 percent of the portfolio is invested in bonds. Some points on the risk-free asset-bond line have lower risk and return than points on the bond-stock frontier; however, we can find no point where, for a given level of risk, the expected return is higher on the risk-free asset-bond line than on the bond-stock frontier. In this case, if we draw the line with the highest slope from the risk-free asset to the bond-stock frontier, that line is tangent to the bond-stock frontier at a point representing a portfolio 100 percent invested in stocks.
396 This CAL is labeled Risk-Free Asset and Large-Cap Stocks in
Figure 11-9. For given assumptions about expected returns, variances, and covariances, that capital allocation line identifies portfolios with the maximum expected return for a given level of risk, if we can spread our money between an optimal risky portfolio and a risk-free asset. Of all lines we could extend from the risk-free rate to the minimum-variance frontier of risky assets, the CAL has maximum slope. Slope defined as rise (expected return) over run (standard deviation) measures the expected risk-return trade-off. The CAL is the line of maximum slope that touches the minimum-variance frontier; consequently, the capital allocation line offers the best risk-return trade-off achievable, given our expectations.
FIGURE 11-9 Portfolios of the Risk-Free Asset, Large-Cap Stocks, and Government Bonds
The previous example showed three important general principles concerning the risk—return trade-off in a portfolio containing a risk-free asset:
• If we can invest in a risk-free asset, then the CAL represents the best risk-return trade-off achievable.
• The CAL has a y-intercept equal to the risk-free rate.
• The CAL is tangent to the efficient frontier of risky assets.
397 EXAMPLE 11-5A The CAL with Multiple Assets
In Example 11-4, the CAL was tangent to the efficient frontier for all risky assets. We now illustrate how the efficient frontier changes depending on the opportunity set (the set of assets available for investment) and whether the investor wants to borrow to leverage his investments. We can illustrate this point by reconsidering our earlier example (Example 11-2) of optimal portfolio choice among the S&P 500, U.S. small-cap stocks, non-U.S. stocks (the MSCI World ex-U.S.), and U.S. government bonds, adding a risk-free asset.
We now assume that the risk-free rate is 5 percent. The standard deviation of the risk-free rate of return is 0, because the return is certain; the covariance between returns to the risk-free asset and returns to the other assets is also 0. We demonstrate the following principles:
• The point of maximum expected return is not the point of tangency between the CAL and the efficient frontier of risky assets.
FIGURE 11-10 The Effect of Adding a Risk-Free Asset to a Risky Portfolio
• The point of tangency between the CAL and the efficient frontier for risky assets represents a portfolio containing risky assets and none of the risk-free asset.
• If we rule out borrowing at the risk-free rate, then the efficient frontier for all the assets (including the risk-free asset) cannot be completely linear.
Figure 11-10 shows the mean-variance frontier for all five assets (the original four plus the risk-free asset), assuming borrowing at the risk-free rate is not possible.
As the figure shows, the efficient frontier is linear from the
y-intercept (the combination of risk and return for placing the entire portfolio in the risk-free asset) to the point of tangency. If the investor wants additional return (and risk) beyond the point of tangency without borrowing, however, the investor’s efficient frontier is the portion of the efficient frontier for the four risky assets that lies to the right of the point of tangency. The investor’s efficient frontier has linear and curved portions.
3982.5.2. The Capital Allocation Line Equation In the previous section, we discussed the graph of the CAL and illustrated how the efficient frontier can change depending on the set of assets available for investment as well as the portfolio manager’s expectations. We now provide the equation for this line.
Suppose that an investor, given expectations about means, variances, and covariances for risky assets, plots the efficient frontier of risky assets. There is a risk-free asset offering a risk-free rate of return,
RF. If
wT is the proportion of the portfolio the investor places in the tangency portfolio, then the expected return for the entire portfolio is
E(Rp)= (1—wT)RF + wT E(RT)
and the standard deviation of the portfolio is
An investor can choose to invest any fraction of his assets in the risk-free asset or in the tangency portfolio; therefore, he can choose many combinations of risk and return. If he puts the entire portfolio in the risk-free asset, then
If he puts his entire portfolio in the tangency portfolio, then
In general, if he puts
wT percent of his portfolio in the tangency portfolio, his portfolio standard deviation will be
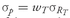
.
To see how the portfolio weights, expected return, and risk are related, we use the relationship
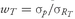
. If we substitute this value of
wT back into the expression for expected return,
E(
Rp)= (1—
wT )
RF + wT E(
RT), we get
or
(11-7)
This equation shows the best possible trade-off between expected risk and return, given this investor’s expectations. The term

is the return that the investor demands in order to take on an extra unit of risk. Example 11-5B illustrates how to calculate the investor’s price of risk and other aspects of his investment using the capital allocation line.
EXAMPLE 11-5B CAL Calculations
Suppose that the risk-free rate, RF, is 5 percent; the expected return to an investor’s tangency portfolio, E(RT), is 15 percent; and the standard deviation of the tangency portfolio is 25 percent.
1. How much return does this investor demand in order to take on an extra unit of risk?
2. Suppose the investor wants a portfolio standard deviation of return of 10 percent. What percentage of the assets should be in the tangency portfolio, and what is the expected return?
3. Suppose the investor wants to put 40 percent of the portfolio in the risk-free asset. What is the portfolio expected return? What is the standard deviation?
4. What expected return should the investor demand for a portfolio with a standard deviation of 35 percent?
5. What combination of the tangency portfolio and the risk-free asset does the investor need to hold in order to have a portfolio with an expected return of 19 percent?
6. If the investor has $10 million to invest, how much must she borrow at the risk-free rate to have a portfolio with an expected return of 19%?
Solution to 1: In this case,

. The investor demands an additional 40 basis points of expected return of the portfolio for every 1 percentage point increase in the standard deviation of portfolio returns.
Solution to 2: Because

, or 40 percent. In other words, 40 percent of the assets are in the tangency portfolio and 60 percent are in the risk-free asset. The expected return for the portfolio is
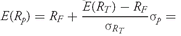
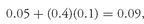
, or 9 percent.
Solution to 3: In this case,
wT = 1 − 0.4 = 0.6. Therefore, the expected portfolio return is
E(
Rp) = (1—
wT )
RF + wT E (
RT ) = (1—0.6)(0.05) + (0.6)(0.15) = 0.11, or 11 percent. The portfolio standard deviation is
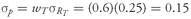
or 15 percent.
Solution to 4: We know that the relation between risk and expected return for this portfolio is
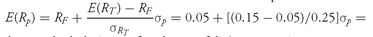

. If the standard deviation for the portfolio’s returns is 35 percent, then the investor can demand an expected return of
E(
Rp) = 0.05 + 0.4σ
p = 0.05 + 0.4(0.35) = 0.19, or 19 percent.
Solution to 5: With an expected return of 19 percent, the asset allocation must be as follows:
How can the weight on the tangency portfolio be 140 percent? The interpretation of wT = 1.4 is that the investment in the tangency portfolio consists of (1) the entire amount of initial wealth and (2) an amount equal to 40 percent of initial wealth that has been borrowed at the risk-free rate. We can confirm that the expected return is (−0.4)(0.05) + (1.4)(0.15) = 0.19 or 19 percent.
Solution to 6: The investor must borrow $4 million dollars at the risk-free rate to increase the holdings of the tangency-asset portfolio to $14 million dollars. Therefore, the net value of the portfolio will be $14million—$4million = $10 million.
In this section, we have assumed that investors may have different views about risky assets’ mean returns, variances of returns, and correlations. Thus each investor may perceive a different efficient frontier of risky assets and have a different tangency portfolio, the optimal portfolio of risky assets which the investor may combine with risk-free borrowing or lending. In the next two sections, we examine the consequences when mean-variance investors share identical expectations.
2.5.3. The Capital Market Line When investors share identical expectations about the mean returns, variance of returns, and correlations of risky assets, the CAL for all investors is the same and is known as the
capital market line (CML). With identical expectations, the tangency portfolio must be the same portfolio for all investors. In equilibrium, this tangency portfolio must be a portfolio containing all risky assets in proportions reflecting their market value weights; the tangency portfolio is the market portfolio of all risky assets. The CML is a capital allocation line with the market portfolio as the tangency portfolio. The equation of the CML is
(11-8)
where
E(Rp ) = the expected return of portfolio p lying on the capital market line
RF = the risk-free rate
E(RM ) = the expected rate of return on the market portfolio
σM = the standard deviation of return on the market portfolio
σp = the standard deviation of return on portfolio p
The slope of the CML, [E(RM) − RF ]/σM, is called the market price of risk because it indicates the market risk premium for each unit of market risk. As noted, the CML describes the expected return of only efficient portfolios. The implication of the capital market line is that all mean – variance investors, whatever their risk tolerance, can satisfy their investment needs by combining the risk-free asset with a single risky portfolio, the market portfolio of all risky assets.
In the next section we present a mean – variance theory describing the expected return of any asset or portfolio, efficient or inefficient.
2.6. The Capital Asset Pricing Model
The capital asset pricing model (CAPM) has played a pivotal role in the development of quantitative investment management since its introduction in the early 1960s. In this section, we review some of its key aspects.
The CAPM makes the following assumptions:
399 • Investors need only know the expected returns, the variances, and the covariances of returns to determine which portfolios are optimal for them. (This assumption appears throughout all of mean – variance theory.)
• Investors have identical views about risky assets’ mean returns, variances of returns, and correlations.
• Investors can buy and sell assets in any quantity without affecting price, and all assets are marketable (can be traded).
• Investors can borrow and lend at the risk-free rate without limit, and they can sell short any asset in any quantity.
• Investors pay no taxes on returns and pay no transaction costs on trades.
The CML represents the efficient frontier when the assumptions of the CAPM hold. In a CAPM world, therefore, all investors can satisfy their investment needs by combining the risk-free asset with the identical tangency portfolio, which is the market portfolio of all risky assets (no risky asset is excluded).
The following equation describes the expected returns on all assets and portfolios, whether efficient or not:
where
E(Ri ) = the expected return on asset i
RF = the risk-free rate of return
E(RM ) = the expected return on the market portfolio
βi = Cov(Ri, RM )/Var(RM )
Equation 11-9 itself is referred to as the
capital asset pricing model, and its graph is called the
security market line (SML). The CAPM is an equation describing the expected return on any asset (or portfolio) as a linear function of its
beta, β
i, which is a measure of the asset’s sensitivity to movements in the market. The CAPM says that expected return has two components: first, the risk-free rate,
RF, and second, an extra return equal to β
i [
E(
RM ) −
RF]. The term [
E(
RM ) −
RF ] is the expected excess return on the market. This amount is the
market risk premium; if we are 100 percent invested in the market, the market risk premium is the extra return we expect to obtain, on average, compared with the risk-free rate of return.
The market risk premium is multiplied by the asset’s beta. A beta of 1 represents average market sensitivity, and we expect an asset with that beta to earn the market risk premium exactly.
400 A beta greater than 1 indicates greater than average market risk and, according to the CAPM, earns a higher expected excess return. Conversely, a beta less than 1 indicates less than average market risk and, according to the CAPM, earns a smaller expected excess return. Expected excess returns are related only to market risk, represented by beta. Sensitivity to the market return is the only source of difference in expected excess returns across assets.
401Like all theory-based models, the CAPM comes from a set of assumptions. The CAPM describes a financial market equilibrium in the sense that, if the model is correct and any asset’s expected return differs from its expected return as given by the CAPM, market forces will come into play to restore the relationships specified by the model. For example, a stock that offers a higher expected return than justified by its beta will be bid up in price, lowering the stock’s expected return; investors would expect that a broad-based portfolio would offset any non-market risk the stock might carry.
Because it is all-inclusive, the market portfolio defined in the CAPM is unobservable. In practice, we must use some broad index to represent it. The CAPM has been used primarily to value equities, so a common choice for the market portfolio is a broad value-weighted stock index or market proxy. The straight-line relationship between expected return and beta results from the efficiency of the market portfolio. As a result, the CAPM theory is equivalent to saying that the unobservable market portfolio is efficient, but not that any particular proxy for the market is efficient.
402 Of more interest to practitioners than the strict truth of CAPM as a theory is whether beta computed using available market proxies is useful for evaluating the expected mean returns to various investment strategies. The evidence now favors the existence of multiple sources of systematic risk affecting the mean returns to investment strategies.
2.7. Mean – Variance Portfolio Choice Rules: An Introduction
In this section, we introduce some of the principles of portfolio choice from a mean – variance perspective. One of the most basic portfolio choice decisions is the selection of an optimal asset allocation starting from a set of permissible asset classes. A second kind of decision involves modifying an existing portfolio. This type of decision is easier because we may be able to conclude that one portfolio represents a mean-variance improvement on another without necessarily establishing that the better portfolio is optimal. We begin with a brief discussion of this second decision type.
2.7.1. Decisions Related to Existing Portfolios We examine two kinds of decisions related to existing portfolios in which mean – variance analysis may play a role.
Comparisons of Portfolios as Stand-Alone Investments The
Markowitz decision rule provides the principle by which a mean – variance investor facing the choice of putting all her money in Asset A or all her money in Asset B can sometimes reach a decision. This investor prefers A to B if either
• the mean return on A is equal to or larger than that on B, but A has a smaller standard deviation of return than B; or
• the mean return on A is strictly larger than that on B, but A and B have the same standard deviation of return.
When A is preferred to B by the Markowitz decision rule, we say that A mean-variance dominates B: Asset A clearly makes more efficient use of risk than B does. For example, if an investor is presented with a choice between (1) an asset allocation A with a mean return of 9 percent and a standard deviation of return of 12 percent and (2) a second asset allocation B with a mean return of 8 percent and a standard deviation of return of 15 percent, a mean – variance investor will prefer alternative A because it is expected to provide a higher mean return with less risk. A point to note is that when asset allocation has both higher mean return and higher standard deviation, the Markowitz decision rule does not select one asset allocation as superior; rather, the preference depends on the individual investor’s risk tolerance.
We can identify an expanded set of mean – variance dominance relationships if we admit borrowing and lending at the risk-free rate. Then we can use the risk-free asset to match risk among the portfolios being compared. The Sharpe ratio (the ratio of mean return in excess of the risk-free rate of return to the standard deviation of return) serves as the appropriate metric.
• If a portfolio
p has a higher positive Sharpe ratio than portfolio
q, then
p mean – variance dominates
q if borrowing and lending at the risk-free rate is possible.
403 Suppose asset allocation A is as before but now B has a mean of 6 percent and a standard deviation of 10 percent. Allocation A has higher mean return than B (9 percent versus 6 percent) but also higher risk (12 percent versus 10 percent), so the Markowitz decision rule is inconclusive about which allocation is better. Suppose we can borrow and lend at a risk-free rate of 3 percent. The Sharpe ratio of A, (9 − 3)/12 = 0.50, is higher than the Sharpe ratio of B, (6 − 3)/10 = 0.30, so we can conclude that A mean – variance dominates B. Note that a portfolio 83.3 percent invested in A and 16.7 percent invested in the risk-free asset has the same standard deviation as B, because 0.833(12) = 10 percent, with mean return of 0.833(9) + 0.167(3) = 8 percent, versus 6 percent for B. In short, we combined the higher Sharpe ratio portfolio p with the risk-free asset to achieve a portfolio with the same risk as portfolio q but with higher mean return. As B was originally defined (mean return of 8 percent and standard deviation of 15 percent), B had a Sharpe ratio of 0.33 and, as expected, the decision based on Sharpe ratios is consistent with that based on the Markowitz decision rule.
Practically, the above decision-making approach is most reliable when we are considering choices among well-diversified portfolios and when the return distributions of the choices are at least approximately normal.
The Decision to Add an Investment to an Existing Portfolio We described an approach for choosing between two asset allocations as an either/or proposition. We now discuss an approach to deciding whether to add a new asset class to an existing portfolio, or more generally to further diversify an existing portfolio.
Suppose you hold a portfolio
p with expected or mean return
E(
Rp) and standard deviation of return σ
p. Then you are offered the opportunity to add another investment to your portfolio, for example, a new asset class. Will you effect a mean – variance improvement by expanding your portfolio to include a positive position in the new investment? To answer this question, you need three inputs:
• the Sharpe ratio of the new investment,
• the Sharpe ratio of the existing portfolio, and
• the correlation between the new investment’s return and portfolio p’s return, Corr(Rnew, Rp ).
Adding the new asset to your portfolio is optimal if the following condition is met:
404
This expression says that in order to gain by adding the new investment to your holdings, the Sharpe ratio of the new investment must be larger than the product of the Sharpe ratio of your existing portfolio and the correlation of the new investment’s returns with the returns of your current portfolio. If
Equation 11-10 holds, we can combine the new investment with the prior holdings to achieve a superior efficient frontier of risky assets (one in which the tangency portfolio has a higher Sharpe ratio). Note that although the expression may indicate that we effect a mean – variance improvement at the margin by adding a positive amount of a new asset, it does not indicate how much of the new asset we might want to add, or more broadly, what the efficient frontier including the new asset may be—to determine it, we would need to conduct an optimization. An insight from
Equation 11-10 is that, in contrast to the case in which we considered investments as stand-alone and needed to consider only Sharpe ratios (from a mean – variance perspective) in choosing among them, in the case in which we can combine two investments, we must also consider their correlation. Example 11-6 illustrates how to use
Equation 11-10 in deciding whether to add an asset class.
EXAMPLE 11-6 The Decision to Add an Asset Class
Jim Regal is chief investment officer of a Canadian pension fund invested in Canadian equities, Canadian bonds, Canadian real estate, and U.S. equities. The portfolio has a Sharpe ratio of 0.25. The investment committee is considering adding one or the other (but not both) of the following asset classes:
• Eurobonds: predicted Sharpe ratio = 0.10; predicted correlation with existing portfolio = 0.42.
• Non-North American developed market equities, as represented in the MSCI EAFE (Europe, Australasia, Far East) index: predicted Sharpe ratio = 0.30; predicted correlation with existing portfolio = 0.67.
1. Explain whether the investment committee should add Eurobonds to the existing portfolio.
2. Explain whether the committee should add non-North American developed market equities to the portfolio.
Solution to 1: (Sharpe ratio of existing portfolio) × (Correlation of Eurobonds with existing portfolio) = 0.25(0.42) = 0.105. We should add Eurobonds if their predicted Sharpe ratio exceeds 0.105. Because the investment committee predicts a Sharpe ratio of 0.10 for Eurobonds, the committee should not add them to the existing portfolio.
Solution to 2: (Sharpe ratio of existing portfolio) × (Correlation of new equity class with existing portfolio) = 0.25(0.67) = 0.1675. Because the predicted Sharpe ratio of 0.30 for non-North American equities exceeds 0.1675, the investment committee should add them to the existing portfolio.
In Example 11-6, even if the correlation between the pension fund’s existing portfolio and the proposed new equity class were +1, so that adding the new asset class had no potential risk reduction benefits,
Equation 11-10 would indicate that the class should be added because the condition for adding the asset class would be satisfied, as 0.30
> 0.25(1.0). For any portfolio, we can always effect a mean – variance improvement at the margin by adding an investment with a higher Sharpe ratio than the existing portfolio. This result is intuitive, because the higher Sharpe ratio investment would mean – variance dominate the existing portfolio in a pairwise comparison. Again, we emphasize that the assumptions of mean – variance analysis must be fulfilled for these results to be reliable.
2.7.2. Determining an Asset Allocation Our objective in this section is to summarize the mean – variance perspective on asset allocation. In a prior section, we gave the mathematical objective and constraints for determining the minimum-variance frontier of risky assets in the simplest case in which the only constraint on portfolio weights is that they sum to 1. Determining the efficient frontier using
Equation 11-3 plus a constraint
wi ≥ 0 to reflect no short sales is a starting point for many institutional investors in determining an asset allocation.
405 Mean – variance theory then points to choosing the asset allocation represented by the perceived tangency portfolio if the investor can borrow or lend at the risk-free rate. The manager can combine the tangency portfolio with the risk-free asset to achieve an efficient portfolio at a desired level of risk. Because the tangency portfolio represents the highest-Sharpe-ratio portfolio of risky assets, it is a logical baseline for an asset allocation.
This theoretical perspective, however, views the investment in a risk-free asset as a readily available risk-adjustment variable. In practice, investors may be constrained against using margin (borrowing), may face constraints concerning minimum and maximum positive investments in a risk-free asset, or may have other reasons for not adopting the perspective of theory.
406 In such a case, the investor may establish an asset allocation among risky asset classes that differs from the tangency portfolio. Quantifying his risk tolerance in terms of standard deviation of returns, the investor could choose the portfolio on the efficient frontier of risky assets that corresponds to the chosen level of standard deviation.
The CAPM framework provides even more narrowly focused choices because it adds the assumption that investors share the same views about mean returns, variances of returns, and correlations. Then all investors would agree on the identity of the tangency portfolio, which is the market portfolio of all risky assets held in proportion to their market values. This portfolio represents the highest possible degree of diversification. The exact identity of such an all-inclusive portfolio cannot be established, of course. Practically, however, investors can own highly diversified passively managed portfolios invested in major asset classes worldwide that approximately reflect the relative market values of the included classes. This asset allocation can be adapted to account for differential expectations. For example, the Black – Litterman (1991, 1992) asset allocation model takes a well-diversified market-value-weighted asset allocation as a neutral starting point for investors. The model incorporates a procedure for deviating from market capitalization weights in directions reflecting an investor’s different-from-equilibrium model (CAPM) views concerning expected returns.
Mean – variance theory in relation to portfolio construction and asset allocation has been intensively examined, and researchers have recognized a number of its limitations. We will discuss an important limitation related to the sensitivity of the optimization procedure—the instability of the efficient frontier—in a later section. We must recognize that as a single-period model, mean – variance analysis ignores the liquidity and tax considerations that arise in a multiperiod world in which investors rebalance portfolios. Relatedly, the time horizon associated with the optimization, often one year, may be shorter than an investor’s actual time horizon due to difficulties in developing inputs for long horizons.
407 Mean – variance analysis takes into account the correlation of returns across asset classes over single time periods but does not address serial correlation (long and short-term dependencies) in returns for a given asset class. Monte Carlo simulation is sometimes used in asset allocation to address such multiperiod issues.
408 Despite its limitations, mean – variance analysis provides an objective and fairly adaptable procedure for narrowing the unlimited set of choices we face in selecting an asset allocation.
409
3. PRACTICAL ISSUES IN MEAN – VARIANCE ANALYSIS
We now discuss practical issues that arise in the application of mean – variance analysis in choosing portfolios. The two areas of focus are
• estimating inputs for mean – variance optimization, and
• the instability of the minimum-variance frontier, which results from the optimization process’s sensitivity to the inputs.
Relative to the first area, we must ask two principal questions concerning the prediction of expected returns, variances, and correlations. First, which methods are feasible? Second, which are most accurate? Relative to sensitivity of the optimization process, we need to ask first, what is the source of the problem, and second, what corrective measures are available to address it.
3.1. Estimating Inputs for Mean – Variance Optimization
In this section, we compare the feasibility and accuracy of several methods for computing the inputs for mean – variance optimization. These methods use one of the following:
• historical means, variances, and correlations,
• historical beta estimated using the market model, or
• adjusted betas.
3.1.1. Historical Estimates This approach involves calculating means, variances, and correlations directly from historical data. The historical method requires estimating a very large number of parameters when we are optimizing for even a moderately large number of assets. As a result, it is more feasible for asset allocation than for portfolio formation involving a large number of stocks.
The number of parameters a portfolio manager needs to estimate to determine the minimum-variance frontier depends on the number of potential stocks in the portfolio. If a portfolio manager has
n stocks in a portfolio and wants to use mean – variance analysis, she must estimate
• n parameters for the expected returns to the stocks,
• n parameters for the variances of the stock returns, and
• n(n − 1)/2 parameters for the covariances of all the stock returns with each other.
Together, the parameters total n2/2 + 3n/2.
The two limitations of the historical approach involve the quantity of estimates needed and the quality of historical estimates of inputs.
The quantity of estimates needed may easily be very large, mainly because the number of covariances increases in the square of the number of securities. If the portfolio manager wanted to compute the minimum-variance frontier for a portfolio of 100 stocks, she would need to estimate 100
2/2 + 3(100)/2 = 5, 150 parameters. If she wanted to compute the minimum-variance frontier for 1,000 stocks, she would need to estimate 501,500 parameters. Not only is this task unappealing, it might be impossible.
410The second limitation is that historical estimates of return parameters typically have substantial estimation error. The problem is least severe for estimates of variances.
411 The problem is acute with historical estimates of mean returns because the variability of risky asset returns is high relative to the mean, and the problem cannot be ameliorated by increasing the frequency of observations. Estimation error is also serious with historical estimates of covariances. The intuition in the case of covariances is that the historical method essentially tries to capture every random feature of a historical data set, reducing the usefulness of the estimates in a predictive mode. In a study based on monthly returns for U.S. stocks over the period 1973 – 1997, Chan, Karceski, and Lakonishok (1999) found that the correlation between past and future sample covariances was 0.34 at the 36-month horizon but only 0.18 at the 12-month horizon.
In current industry practice, the historical sample covariance matrix is not used without adjustment in mean – variance optimization. Adjusted values of variance and covariance may be weighted averages of the raw sample values and the average variance or covariance, respectively. For example, if a stock’s variance of monthly returns is 0.0210 and the average stock’s variance of monthly returns is 0.0098, the procedure might adjust 0.0210 downward, in the direction of the mean. Adjusting values in the direction of the mean reduces the dispersion in the estimates that may be caused by sampling error.
412In estimating mean returns, analysts use a variety of approaches. They may adjust historical mean returns to reflect perceived contrasts between current market conditions and past average experience. They frequently use valuation models, such as models based on expected future cash flows, or equilibrium models, such as the CAPM, to develop forward-looking mean return estimates. Their use of these approaches reflects not only the technical issue of estimation error but also the risk in assuming that future performance will mirror past average performance.
3.1.2. Market Model Estimates: Historical Beta (Unadjusted) A simpler way to compute the variances and covariances of asset returns involves the insight that asset returns may be related to each other through their correlation with a limited set of variables or factors. The simplest such model is the market model, which describes a regression relationship between the returns on an asset and the returns on the market portfolio. For asset
i, the return to the asset can be modeled as
where
Ri = the return on asset i
RM = the return on the market portfolio
αi = average return on asset i unrelated to the market return
βi = the sensitivity of the return on asset i to the return on the market portfolio
= an error term
Consider first how to interpret βi. If the market return increases by one percentage point, the market model predicts that the return to asset i will increase by βi percentage points. (Recall that βi is the slope in the market model.)
Now consider how to interpret αi. If the market return is 0, the market model predicts that the return to asset i will be αi, the intercept in the market model.
The market model makes the following assumptions about the terms in
Equation 11-11:
• The expected value of the error term is 0, so
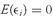
.
• The market return (
RM) is uncorrelated with the error term,

.
• The error terms, ∈
i, are uncorrelated among different assets. For example, the error term for asset
i is uncorrelated with the error term for asset
j. Consequently,

for all
i not equal to
j.
413 Note that some of these assumptions are very similar to those we made about the single-variable linear regression model in the chapter on correlation and regression. The market model, however, does not assume that the error term is normally distributed or that the variance of the error term is identical across assets.
Given these assumptions, the market model makes the following predictions about the expected returns of assets as well as the variances and covariances of asset returns.
414First, the expected return for asset i depends on the expected return to the market, E(RM ), the sensitivity of the return on asset i to the return on the market, βi, and the part of returns on asset i that are independent of market returns, αi.
(11-12)
Second, the variance of the return to asset
i depends on the variance of the return to the market,

, the variance of the error for the return of asset
i in the market model,
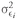
, and the sensitivity, β
i.
In the context of a model in which the market portfolio is the only source of risk, the first term in
Equation 11-13,

, is sometimes referred to as the systematic risk of asset
i. The error variance term in
Equation 11-13,

, is sometimes referred to as the nonsystematic risk of asset
i.
Third, the covariance of the return to asset
i and the return to asset
j depends on the variance of the return to the market,

, and on the sensitivities β
i and β
j.
We can use the market model to greatly reduce the computational task of providing the inputs to a mean—variance optimization. For each of the
n assets, we need to know α
i, β
i,
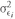
, as well as the expected return and variance for the market. Because we need to estimate only 3
n + 2 parameters with the market model, we need far fewer parameters to construct the minimum-variance frontier than we would if we estimated the historical means, variances, and covariances of asset returns. For example, if we estimated the minimum-variance frontier for 1,000 assets (say, 1,000 different stocks), the market model would use 3,002 parameters for computing the minimum-variance frontier, whereas the historical estimates approach would require 501,500 parameters, as discussed earlier.
We do not know the parameters of the market model, so we must estimate them. But what method do we use? The most convenient way is to estimate a linear regression using time-series data on the returns to the market and the returns to each asset.
We can use the market model to estimate α
i and β
i by using a separate linear regression for each asset, using historical data on asset returns and market returns.
415 The regression output produces an estimate,
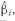
, of β
i; we call this estimate an unadjusted beta. Later we will introduce an adjusted beta. We can use these estimates to compute the expected returns and the variances and covariances of those returns for mean—variance optimization.
EXAMPLE 11-7 Computing Stock Correlations Using the Market Model
You are estimating the correlation of returns between Cisco Systems (Nasdaq: CSCO) and Microsoft (Nasdaq: MSFT) as of late 2003. You run a market-model regression for each of the two stocks based on monthly returns, using the S&P 500 to represent the market. You obtain the following regression results:
• The estimated beta for Cisco,
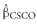
, is 2.09, and the residual standard deviation,

, is 11.52.
• The estimated beta for Microsoft,

, is 1.75, and the residual standard deviation,

, is 11.26.
Your estimate of the variance of monthly returns on the S&P 500 is
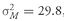
, which corresponds to an annual standard deviation of returns of about 18.9 percent. Using the data given, estimate the correlation of returns between Cisco and Microsoft.
Solution: We compute

and
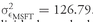
. Using the definition of correlation as covariance divided by the individual standard deviations, and using
Equations 11-13 and
11-14, we have
Thus the market model predicts that the correlation between the two asset returns is 0.4552.
One difficulty with using the market model is determining an appropriate index to represent the market. Typically, analysts who use the market model to determine the risk of individual domestic equities use returns on a domestic equity market index. In the United States, such an index might be the S&P 500 or the Wilshire 5000 Index; in the United Kingdom, the Financial Times Stock Exchange 100 Index might be used. Using returns on an equity market index may create a reasonable market model for equities, but it may not be reasonable for modeling the risk of other asset classes.
416
3.1.3. Market Model Estimates: Adjusted Beta Should we use historical betas from a market model for mean—variance optimization? Before we can answer this question, we need to restate our goal: We want to predict expected returns for a set of assets and the variances and covariances of those returns so that we can estimate the minimum-variance frontier for those assets. Estimates based on historical beta depend on the crucial assumption that the historical beta for a particular asset is the best predictor of the future beta for that asset. If beta changes over time, then this assumption is untrue. Therefore, we may want to use some other measure instead of historical beta to estimate an asset’s future beta. These other forecasts are known by the general term adjusted beta. Researchers have shown that adjusted beta is often a better forecast of future beta than is historical beta. As a consequence, practitioners often use adjusted beta.
Suppose, for example, we are in period t and we want to estimate the minimum-variance frontier for period t + 1 for a set of stocks. We need to use data available in period t to predict the expected stock returns and the variances and covariances of those returns in period t + 1. Note, however, that the historical estimate of beta in period t for a particular stock may not be the best estimate we can make in period t of beta in period t + 1 for that stock. And the minimum-variance frontier for period t + 1 must be based on the forecast of beta for period t + 1.
If beta for each stock were a random walk from one period to the next, then we could write the relation between the beta for stock
i in period
t and the beta for stock
i in period
t + 1 as
where
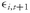
is an error term. If beta followed a random walk, the best predictor of β
i,t +1 would be β
i,t because the error term has a mean value of 0. The historical beta would be the best predictor of the future beta, and the historical beta need not be adjusted.
In reality, beta for each stock often is not a random walk from one period to the next, and therefore, historical beta is not necessarily the best predictor of the future beta. For example, if beta can be represented as a first-order autoregression, then
If we estimate
Equation 11-15 using time-series data on historical betas, the best predictor of β
i,t+1 is
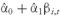
. In this case, the historical beta needs to be adjusted because the best prediction of beta in the next period is

, not β
i,t.
Adjusted betas predict future betas better than historical betas do because betas are, on average, mean reverting.
417 Therefore, we should use adjusted, rather than historical, betas. One common method that practitioners use to adjust historical beta is to assume that α
0 = 0.333 and α
1 = 0.667. With this adjustment,
• if the historical beta equals 1.0, then the adjusted beta will be 0.333 + 0.667(1.0) = 1.0.
• if the historical beta equals 1.5, then adjusted beta will be 0.333 + 0.667(1.5) = 1.333.
• if the historical beta equals 0.5, then adjusted beta will be 0.333 + 0.667(0.5) = 0.667.
Thus the mean-reverting level of beta is 1.0. If the historical beta is above 1.0, then adjusted beta will be below historical beta; if historical beta is below 1.0, then adjusted beta will be above historical beta.45
45 Although practitioners regularly use this method for computing adjusted beta, we are unaware of any published research suggesting that α0 = 0.333 and α1 = 0.667 are the best coefficient values to use in computing adjusted beta. Some researchers suggest an additional adjustment to historical betas called fundamental betas. Fundamental betas predict beta based on fundamental data for a company (price—earnings ratio, earnings growth, market capitalization, volatility, and so forth). Consulting firms such as BARRA sell estimates of fundamental betas.
3.2. Instability in the Minimum-Variance Frontier
Although standard mean—variance optimization, as represented by
Equation 11-3, is a convenient and objective procedure for portfolio formation, we must use care when interpreting its results in practice. In this section, we discuss cautions regarding the use of mean—variance optimization. The problems that can arise have been widely studied, and remedies for them have been developed. With this knowledge, mean—variance optimization can still be a useful tool.
The chief problem with mean—variance optimization is that small changes in input assumptions can lead to large changes in the minimum-variance (and efficient) frontier. This problem is called instability in the minimum-variance frontier. It arises because, in practice, uncertainty exists about the expected returns, variances, and covariances used in tracing out the minimum-variance frontier.
Suppose, for example, that we use historical data to compute estimates to be used in an optimization. These means, variances, and covariances are sample quantities that are subject to random variation. In the chapter on sampling, for instance, we discussed how the sample mean has a probability distribution, called its sampling distribution. The sample mean is only a point estimate of the underlying or population mean.
418 The optimization process attempts to maximally exploit differences among assets. When these differences are statistically (and economically) insignificant (e.g., representing random variation), the resulting minimumvariance frontiers are misleading and not practically useful. Mean—variance optimization then overfits the data: It does too much with differences that are actually not meaningful. In an optimization with no limitation on short sales, assets can appear with very large negative weights, reflecting this overfitting (a negative weight for an asset means that the asset is sold short). Portfolios with very large short positions are of little practical interest.
419 Because of sensitivity to small changes in inputs, mean—variance optimizations may suggest too-frequent portfolio rebalancing, which is costly. Responses to instability include the following:
• Adding constraints against short sales (which is sometimes an institutional investment policy constraint as well). In
Equation 11-3, we can add a no-short-sales constraint specifying that all asset weights must be positive:
wj ≥ 0,
j = 1, 2, 3, . . . ,
n.
420 • Improving the statistical quality of inputs to optimization.
• Using a statistical concept of the efficient frontier, reflecting the fact that the inputs to the optimization are random variables rather than constants.
421 We stated above that mean—variance optimizations can recommend too-frequent portfolio rebalancing. Similarly, we find that the minimum-variance frontier is generally unstable when calculated using historical data for different time periods. One possible explanation is that the different frontiers reflect shifts in the parameters of asset return distribution between sample time periods. Time instability of the minimum-variance frontier can also result from random variation in means, variances, and covariances, when the underlying parameters are actually unchanged. Small differences in sample periods used for mean—variance optimization may greatly affect a model even if the distribution of asset returns is stationary. Example 11-8 illustrates time instability with the data used for optimization.
EXAMPLE 11-8 Time Instability of the Minimum-Variance Frontier
In Example 11-2, we calculated a minimum-variance frontier for four asset classes for the period 1970 through 2002. What variation would we find among minimumvariance frontiers for subperiods of 1970 to 2002? To find out, we take the data for decades within the entire period, calculate the sample statistics, and then trace out the minimum-variance frontier for each decade.
Table 11-10 shows the sample statistics of the monthly asset returns to these four asset classes for 1970 to 1979, 1980 to 1989, 1990 to 2002, and the combined sample period.
TABLE 11-10 Average Returns, Standard Deviations, and Correlation Matrixes
Source: Ibbotson Associates.
As we might expect, variation occurs within subperiods in the sample means, variances, and covariances for all asset classes. Initially, the correlations offer the impression of relative stability over time. For example, the correlation of the S&P 500 with the MSCI World ex-U.S. was 0.544, 0.512, and 0.647 for 1970 to 1979, 1980 to 1989, and 1990 to 2002, respectively. In contrast to ranking by mean returns, the ranking of asset classes by standard deviation was the same in each decade, with U.S. small-cap stocks the riskiest asset class and bonds the least risky. We could use statistical inference to explore interperiod differences. With these initial impressions in mind, however, let us view the decades’ minimum-variance frontiers.
Figure 11-11 shows the minimum-variance frontiers computed using the historical return statistics shown in
Table 11-10 for 1970 to 1979, 1980 to 1989, 1990 to 2002, and the entire sample period. As this figure shows, the minimum-variance frontiers can differ dramatically in different periods. For example, note that the minimum-variance frontiers based on data from 1970 to 1979 and 1980 to 1989 do not overlap at all.
FIGURE 11-11 Historical Minimum—Variance Frontier Comparison
As mentioned, researchers have developed various methods to address portfolio managers’ concerns about the issue of instability.
EXAMPLE 11-9 How Yale University’s Endowment Fund Uses Mean—Variance Analysis
David Swensen, Yale University’s chief investment officer (who also teaches portfolio management at Yale), wrote that “unconstrained mean—variance [optimization] usually provide[s] solutions unrecognizable as reasonable portfolios . . . . Because the process involves material simplifying assumptions, adopting the unconstrained asset allocation point estimates produced by mean—variance optimization makes little sense.”
422Swensen’s remarks highlight practitioners’ concerns about the usefulness of standard mean—variance optimization. Among the most important simplifying assumptions of mean—variance analysis is that the means, variances, and covariances of assets in a portfolio are known. Because the optimization process tries to make much of small differences, and the true values of the means and other parameters are uncertain, this simplifying assumption has a large impact. As mentioned earlier, responses to instability include adding constraints on asset weights and modifying historical sample estimates of the inputs. Despite Swensen’s criticism, Yale uses mean—variance analysis for allocating its portfolio; however, the Yale Investment Office adds constraints on weights and does not use raw historical inputs.
4. MULTIFACTOR MODELS
Earlier we discussed the market model, which was historically the first attempt to describe the process that drives asset returns. The market model assumes that all explainable variation in asset returns is related to a single factor, the return to the market. Yet asset returns may be related to factors other than market return, such as interest rate movements, inflation, or industry-specific returns. For many years, investment professionals have used multifactor models in portfolio management, risk analysis, and the evaluation of portfolio performance.
Multifactor models have gained importance for the practical business of portfolio management for two main reasons. First, multifactor models explain asset returns better than the market model does.
423 Second, multifactor models provide a more detailed analysis of risk than does a single factor model. That greater level of detail is useful in both passive and active management.
• Passive management. In managing a fund that seeks to track an index with many component securities, portfolio managers may need to select a sample of securities from the index. Analysts can use multifactor models to match an index fund’s factor exposures to the factor exposures of the index tracked.
• Active management. Multifactor models are used in portfolio formation to model the expected returns and risks of securities and portfolio. Many quantitative investment managers rely on multifactor models in predicting alpha (excess risk-adjusted returns) or relative return (the return on one asset or asset class relative to that of another) as part of a variety of active investment strategies. In evaluating portfolios, analysts use multifactor models to understand the sources of active managers’ returns and assess the risks assumed relative to the manager’s benchmark (comparison portfolio).
In the following sections, we explain the basic principles of factor models and discuss various types of models and their application. We also present the arbitrage pricing theory developed by Ross (1976), which relates the expected return of investments to their risk with respect to a set of factors.
4.1. Factors and Types of Multifactor Models
To begin by defining terms, a factor is a common or underlying element with which several variables are correlated. For example, the market factor is an underlying element with which individual share returns are correlated. We search for systematic factors, which affect the average returns of a large number of different assets. These factors represent priced risk, risk for which investors require an additional return for bearing. Systematic factors should thus help explain returns.
Many varieties of multifactor models have been proposed and researched. We can categorize most of them into three main groups, according to the type of factor used:
• In macroeconomic factor models, the factors are surprises in macroeconomic variables that significantly explain equity returns. The factors can be understood as affecting either the expected future cash flows of companies or the interest rate used to discount these cash flows back to the present.
• In fundamental factor models, the factors are attributes of stocks or companies that are important in explaining cross-sectional differences in stock prices. Among the fundamental factors that have been used are the book-value-to-price ratio, market capitalization, the price—earnings ratio, and financial leverage.
• In statistical factor models, statistical methods are applied to a set of historical returns to determine portfolios that explain historical returns in one of two senses. In factor analysis models, the factors are the portfolios that best explain (reproduce) historical return covariances. In principal-components models, the factors are portfolios that best explain (reproduce) the historical return variances.
Some practical factor models have the characteristics of more than one of the above categories. We can call such models mixed factor models.
Our discussion concentrates on macroeconomic factor models and fundamental factor models. Industry use has generally favored fundamental and macroeconomic models, perhaps because such models are much more easily interpreted; nevertheless, statistical factor models have proponents and are used in practical applications.
4.2. The Structure of Macroeconomic Factor Models
The representation of returns in macroeconomic factor models assumes that the returns to each asset are correlated with only the surprises in some factors related to the aggregate economy, such as inflation or real output.
424 We can define
surprise in general as the actual value minus predicted (or expected) value. A factor’s surprise is the component of the factor’s return that was unexpected, and the factor surprises constitute the model’s independent variables. This idea contrasts to the representation of independent variables as returns (as opposed to the surprise in returns) in fundamental factor models, or for that matter in the market model.
Suppose that
K factors explain asset returns. Then in a macroeconomic factor model, the following equation expresses the return of asset
i:
where
Ri = the return to asset i
ai = the expected return to asset i
Fk = the surprise in the factor k, k = 1, 2, . . . , K
bik = the sensitivity of the return on asset i to a surprise in factor k, k = 1, 2, . . . , K
∈i = an error term with a zero mean that represents the portion of the return to asset i not explained by the factor model
What exactly do we mean by the surprise in a macroeconomic factor? Suppose we are analyzing monthly returns for stocks. At the beginning of each month, we have a prediction of inflation for the month. The prediction may come from an econometric model or a professional economic forecaster, for example. Suppose our forecast at the beginning of the month is that inflation will be 0.4 percent during the month. At the end of the month, we find that inflation was actually 0.5 percent during the month. During any month,
Actual inflation = Predicted inflation + Surprise inflation
In this case, actual inflation was 0.5 percent and predicted inflation was 0.4 percent. Therefore, the surprise in inflation was 0.5 − 0.4 = 0.1 percent.
What is the effect of defining the factors in terms of surprises? Suppose we believe that inflation and gross domestic product (GDP) growth are priced risk. (GDP is a money measure of the goods and services produced within a country’s borders.) We do not use the predicted values of these variables because the predicted values are already reflected in stock prices and thus in their expected returns. The intercept ai, the expected return to asset i, reflects the effect of the predicted values of the macroeconomic variables on expected stock returns. The surprise in the macroeconomic variables during the month, on the other hand, contains new information about the variable. As a result, this model structure analyzes the return to an asset into three components: the asset’s expected return, its unexpected return resulting from new information about the factors, and an error term.
Consider a factor model in which the returns to each asset are correlated with two factors. For example, we might assume that the returns for a particular stock are correlated with surprises in interest rates and surprises in GDP growth. For stock
i, the return to the stock can be modeled as
where
Ri = the return to stock i
ai = the expected return to stock i
bi1 = the sensitivity of the return to stock i to interest rate surprises
FINT = the surprise in interest rates
bi2 = the sensitivity of the return to stock i to GDP growth surprises
FGDP = the surprise in GDP growth
∈i = an error term with a zero mean that represents the portion of the return to asset i not explained by the factor model
Consider first how to interpret
bi1. The factor model predicts that a one percentage point surprise in interest rates will contribute
bi1 percentage points to the return to stock
i. The slope coefficient
bi2 has a similar interpretation relative to the GDP growth factor. Thus slope coefficients are naturally interpreted as the factor sensitivities of the asset.
425 A
factor sensitivity is a measure of the response of return to each unit of increase in a factor, holding all other factors constant.
Now consider how to interpret the intercept ai. Recall that the error term has a mean or average value of 0. If the surprises in both interest rates and GDP growth are 0, the factor model predicts that the return to asset i will be ai. Thus ai is the expected value of the return to stock i.
Finally, consider the error term ∈i. The intercept ai represents the asset’s expected return. The amount (bi1 FINT + bi2 FGDP) represents the return resulting from factor surprises, and we have interpreted these as the sources of risk shared with other assets. The term ∈i is the part of return that is unexplained by expected return or the factor surprises. If we have adequately represented the sources of common risk (the factors), then ∈i must represent an asset-specific risk. For a stock, it might represent the return from an unanticipated company-specific event.
We will discuss expected returns further when we present the arbitrage pricing theory. In macroeconomic factor models, the time series of factor surprises are developed first. We use regression analysis to estimate assets’ sensitivities to the factors. In our discussion, we assume that you do not estimate sensitivities and intercepts yourself; instead you use estimates from another source (for example, one of the many consulting companies that specialize in factor models).
426 When we have the parameters for the individual assets in a portfolio, we can calculate the portfolio’s parameters as a weighted average of the parameters of individual assets. An individual asset’s weight in that calculation is the proportion of the total market value of the portfolio that the individual asset represents.
EXAMPLE 11-10 Factor Sensitivities for a Two-Stock Portfolio
Suppose that stock returns are affected by two common factors: surprises in inflation and surprises in GDP growth. A portfolio manager is analyzing the returns on a portfolio of two stocks, Manumatic (MANM) and Nextech (NXT). The following equations describe the returns for those stocks, where the factors
FINFL and
FGDP represent the surprise in inflation and GDP growth, respectively:
In evaluating the equations for surprises in inflation and GDP, amounts stated in percent terms need to be converted to decimal form. One-third of the portfolio is invested in Manumatic stock, and two-thirds is invested in Nextech stock.
1. Formulate an expression for the return on the portfolio.
2. State the expected return on the portfolio.
3. Calculate the return on the portfolio given that the surprises in inflation and GDP growth are 1 percent and 0 percent, respectively, assuming that the error terms for MANM and NXT both equal 0.5 percent.
Solution to 1: The portfolio’s return is the following weighted average of the returns to the two stocks:
Solution to 2: The expected return on the portfolio is 11 percent, the value of the intercept in the expression obtained in Part 1.
4.3. Arbitrage Pricing Theory and the Factor Model
In the 1970s, Stephen Ross developed the arbitrage pricing theory (APT) as an alternative to the CAPM. APT describes the expected return on an asset (or portfolio) as a linear function of the risk of the asset (or portfolio) with respect to a set of factors. Like the CAPM, the APT describes a financial market equilibrium. However, the APT makes less-strong assumptions than the CAPM. The APT relies on three assumptions:
1. A factor model describes asset returns.
2. There are many assets, so investors can form well-diversified portfolios that eliminate asset-specific risk.
3. No arbitrage opportunities exist among well-diversified portfolios.
Arbitrage is a risk-free operation that earns an expected positive net profit but requires no net investment of money.
427 An
arbitrage opportunity is an opportunity to conduct an arbitrage—an opportunity to earn an expected positive net profit without risk and with no net investment of money.
In the first assumption, the number of factors is not specified. The second assumption allows us to form portfolios with factor risk but without asset-specific risk. The third assumption is the condition of financial market equilibrium.
Empirical evidence indicates that Assumption 2 is reasonable. When a portfolio contains many stocks, the asset-specific or nonsystematic risk of individual stocks makes almost no contribution to the variance of portfolio returns. Roll and Ross (2001) found that only 1 percent to 3 percent of a well-diversified portfolio’s variance comes from the nonsystematic variance of the individual stocks in the portfolio, as
Figure 11-12 shows.
According to the APT, if the above three assumptions hold, the following equation holds:
428
where
E(Rp) = the expected return to portfolio p
RF = the risk-free rate
λj = the risk premium for factor j
βp,j = the sensitivity of the portfolio to factor j
K = the number of factors
The APT equation,
Equation 11-18, says that the expected return on any well-diversified portfolio is linearly related to the factor sensitivities of that portfolio.
429FIGURE 11-12 Sources of Volatility: The Case of a Well Diversified Portfolio
The factor risk premium (or factor price) λj represents the expected return in excess of the risk-free rate for a portfolio with a sensitivity of 1 to factor j and a sensitivity of 0 to all other factors. Such a portfolio is called a pure factor portfolio for factor j.
For example, suppose we have a portfolio with a sensitivity of 1 with respect to Factor 1 and a sensitivity of 0 to all other factors. With
E1 being the expected return on this portfolio,
Equation 11-18 shows that the expected return on this portfolio is
E1 =
RF + λ
1 × 1, so λ
1 =
E1 −
RF. Suppose that
E1 = 0.12 and
RF = 0.04. Then the risk premium for Factor 1 is λ
1 = 0.12 − 0.04 = 0.08 or 8 percent. We obtain an eight percentage point increase in expected return for an increase of 1 in the sensitivity to first factor.
What is the relationship between the APT equation and the equation for a multifactor model,
Equation 11-17? In discussing the multifactor model, we stated that the intercept term is the investment’s expected return. The APT equation explains what an investment’s expected return is in equilibrium. Thus if the APT holds, it places a restriction on the intercept term in the multifactor model in the sense that the APT model tells us what the intercept’s value should be. For instance, in Example 11-10, the APT would explain the intercept of 0.09 in the model for MANM returns as the expected return on MANM given the stock’s sensitivities to the inflation and GDP factors and the risk premiums of the those factors. We can in fact substitute the APT equation into the multifactor model to produce what is known as an APT model in returns form.
430To use the APT equation, we need to estimate its parameters. The parameters of the APT equation are the risk-free rate and the factor risk premiums (the factor sensitivities are specific to individual investments). Example 11-11 shows how the expected returns and factor sensitivities of a set of portfolios can determine the parameters of the APT model assuming a single factor.
EXAMPLE 11-11 Determining the Parameters in a One-Factor APT Model
Suppose we have three well-diversified portfolios that are each sensitive to the same single factor.
Table 11-11 shows the expected returns and factor sensitivities of these portfolios. Assume that the expected returns reflect a one-year investment horizon.
| Portfolio | Expected Return | Factor Sensitivity |
|---|
| A | 0.075 | 0.5 |
| B | 0.150 | 2.0 |
| C | 0.070 | 0.4 |
We can use these data to determine the parameters of the APT equation. According to
Equation 11-18, for any well-diversified portfolio and assuming a single factor explains returns, we have
E(
Rp) =
RF + λ
1β
p,1. The factor sensitivities and expected returns are known; thus there are two unknowns, the parameters
RF and λ
1 . Because two points define a straight line, we need to set up only two equations. Selecting Portfolios A and B, we have
E(RA) = 0.075 = RF + 0.5λ1
and
From the equation for Portfolio A, we have
RF = 0.075 − 0.5λ
1. Substituting this expression for the risk-free rate into the equation for Portfolio B gives
So we have λ
1 = (0.15 − 0.075)/1.5 = 0.05. Substituting this value for λ
1 back into the equation for the expected return to Portfolio A yields
So the risk-free rate is 0.05 or 5 percent, and the factor premium for the common factor is also 0.05 or 5 percent. The APT equation is
Portfolio C has a factor sensitivity of 0.4. Accordingly, 0.05 + (0.05 × 0.4) = 0.07 or 7 percent if no arbitrage opportunity exists. The expected return for Portfolio C given in
Table 11-11 is 7 percent. Therefore, in this example no arbitrage opportunity exists.
EXAMPLE 11-12 Checking Whether Portfolio Returns Are Consistent with No Arbitrage
In this example, we demonstrate how to tell whether a set of expected returns for well-diversified portfolios is consistent with the APT by testing whether an arbitrage opportunity exists. In Example 11-11, we had three portfolios with expected returns and factor sensitivities that were consistent with the one-factor APT model
E(
Rp) = 0.05 + 0.05β
p,1. Suppose we expand the set of portfolios to include a fourth well-diversified portfolio, Portfolio D.
Table 11-12 repeats the data given in
Table 11-11 for Portfolios A, B, and C, in addition to providing data on Portfolio D and a portfolio we form using A and C.
| Portfolio | Expected Return | Factor Sensitivity |
|---|
| A | 0.0750 | 0.50 |
| B | 0.1500 | 2.00 |
| C | 0.0700 | 0.40 |
| D | 0.0800 | 0.45 |
| 0.5A + 0.5C | 0.0725 | 0.45 |
The expected return and factor sensitivity of a portfolio is the weighted average of the expected returns and factor sensitivities of the assets in the portfolio. Suppose we construct a portfolio consisting of 50 percent Portfolio A and 50 percent Portfolio C.
Table 11-12 shows that the expected return of this portfolio is (0.50)(0.0750) + (0.50)(0.07) = 0.0725, or 7.25 percent. The factor sensitivity of this portfolio is (0.50)(0.50) + (0.50)(0.40) = 0.45.
Arbitrage pricing theory assumes that well-diversified portfolios present no arbitrage opportunities. If the initial investment is 0 and we bear no risk, the final expected cash flow should be 0. In this case, the configuration of expected returns in relation to factor risk presents an arbitrage opportunity involving Portfolios A, C, and D. Portfolio D offers too high an expected rate of return given its factor sensitivity. According to the APT model estimated in Example 11-11, an arbitrage opportunity exists unless E (RD ) = 0.05 + 0.05βD,1 = 0.05 + (0.05 × 0.45) = 0.0725, so that the expected return on D is 7.25 percent. In fact, the expected return on D is 8 percent. Portfolio D is undervalued relative to its factor risk. We will buy D (hold it long) in the portfolio that exploits the arbitrage opportunity (the arbitrage portfolio). We purchase D using the proceeds from selling short a portfolio consisting of A and C with exactly the same 0.45 factor sensitivity as D. As we showed above, an equally weighted portfolio of A and C has a factor sensitivity of 0.45.
The arbitrage thus involves the following strategy: Invest $10,000 in Portfolio D and fund that investment by selling short an equally weighted portfolio of Portfolios A and C; then close out the investment position at the end of one year (the investment horizon for expected returns).
Table 11-13 demonstrates the arbitrage profits to the arbitrage strategy. The final row of the table shows the net cash flow to the arbitrage portfolio.
TABLE 11-13 Arbitrage Opportunity within Sample Portfolios
As
Table 11-13 shows, if we buy $10,000 of Portfolio D and sell $10,000 of an equally weighted portfolio of Portfolios A and C, we have an initial net cash flow of $0. The expected value of our investment in Portfolio D at the end of one year is $10, 000(1 + 0.08) = $10, 800. The expected value of our short position in Portfolios A and C at the end of one year is -$10, 000(1.0725) = -$10, 725. So the combined expected cash flow from our investment position in one year is $75.
What about the risk?
Table 11-13 shows that the factor risk has been eliminated: Purchasing D and selling short an equally weighted portfolio of A and C creates a portfolio with a factor sensitivity of 0.45 – 0.45 = 0. The portfolios are well diversified, and we assume any asset-specific risk is negligible.
Because the arbitrage is possible, Portfolios A, C, and D cannot all be consistent with the same equilibrium. A unique set of parameters for the APT model does not describe the returns on these three portfolios. If Portfolio D actually had an expected return of 8 percent, investors would bid up its price until the expected return fell and the arbitrage opportunity vanished. Thus arbitrage restores equilibrium relationships among expected returns.
In Example 11-11, we illustrated how the parameters of a single-factor APT model can be determined from data. Example 11-13 shows how to determine the model parameters in a model with more than one factor.
EXAMPLE 11-13 Determining the Parameters in a Two-Factor Model
Suppose that two factors, surprise in inflation (Factor 1) and surprise in GDP growth (Factor 2), explain returns. According to the APT, an arbitrage opportunity exists unless
E(Rp) = RF + λ1βp,1 + λ2βp,2
Our goal is to estimate the three parameters of the model,
RF, λ
1, and λ
2. We also have hypothetical data on three well-diversified portfolios, J, K, and L, given in
Table 11-14.
If the market is in equilibrium (no arbitrage opportunities exist), the expected returns to the three portfolios should be described by the two-factor APT with the same set of parameters. Using the expected returns and the return sensitivities shown in
Table 11-14 yields
We have three equations with three unknowns, so we can solve for the parameters using the method of substitution. We first want to get two equations with two unknowns. Solving the equation for
E(
RJ) for the risk-free rate,
RF = 0.14 – 1.0λ1 – 1.5λ2
Substituting this expression for the risk-free rate into the equation for
E(
RK ), we find, after simplification, that λ
1 = 0.04 – λ
2. Using λ
1 = 0.04 – λ
2 to eliminate λ
1 in the equation for
E(
RJ),
Using λ
1 = 0.04 – λ
2 to eliminate λ
1 in the equation for
E(
RL),
Using the two equations in
RF and λ
2 immediately above, we find that λ
2 = 0.06 (we solved for the risk-free rate in the first of these two equations and used the expression in the second equation). Because λ
1 = 0.04 – λ
2, λ
1 = – 0.02. Finally,
RF = 0.14 – 1.0 × ( – 0.02) – 1.5 × (0.06) = 0.07. To summarize:
RF = 0.07 (The risk-free rate is 7 percent.)
λ1 = – 0.02 (The inflation risk premium is −2 percent per unit of sensitivity.)
λ2 = 0.06 (The GDP risk premium is 6 percent per unit of sensitivity.)
So, the APT equation for these three portfolios is
E(Rp) = 0.07 – 0.02βp,1 + 0.06βp,2
This example illustrates the calculations for determining the parameters of an APT model. It also shows that the risk premium for a factor can actually be negative.
In Example 11-13, we computed a negative risk premium for the inflation factor. One explanation for a negative inflation risk premium is that most equities have negative sensitivities to inflation risk (their returns tend to decrease with a positive inflation surprise). An asset with a positive inflation sensitivity would be in demand as an inflation-hedging asset; the premium associated with a factor portfolio for inflation risk could be negative as a result.
4.4. The Structure of Fundamental Factor Models
We earlier gave the equation of a macroeconomic factor model as
Ri = ai + bi1F1 + bi2F2 + · · · + biK FK + εi
We can also represent the structure of fundamental factor models with this equation, but we need to interpret the terms differently.
In fundamental factor models, the factors are stated as returns rather than return surprises in relation to predicted values, so they do not generally have expected values of zero. This approach changes the interpretation of the intercept, which we no longer interpret as the expected return.
431We also interpret the factor sensitivities differently in most fundamental factor models. In fundamental factor models, the factor sensitivities are attributes of the security. Consider a fundamental model for equities with a dividend yield factor. An asset’s sensitivity to the dividend factor is the value of the attribute itself, its dividend yield; the sensitivity is typically standardized. Specifically, an asset
i’s sensitivity to a given factor would be calculated as the value of the attribute for the asset minus the average value of the attribute across all stocks, divided by the standard deviation of the attribute across all stocks. The
standardized beta is
Continuing with the dividend yield example, after standardization a stock with an average dividend yield will have a factor sensitivity of 0, a stock with a dividend yield one standard deviation above the average will have a factor sensitivity of 1, and a stock with a dividend yield one standard deviation below the average will have a factor sensitivity of −1. Suppose, for example, that an investment has a dividend yield of 3.5 percent and that the average dividend yield across all stocks being considered is 2.5 percent. Further, suppose that the standard deviation of dividend yields across all stocks is 2 percent. The investment’s sensitivity to dividend yield is (3.5% – 2.5%)/2% = 0.50, or one-half standard deviation above average. The scaling permits all factor sensitivities to be interpreted similarly, despite differences in units of measure and scale in the variables. The exception to this interpretation is factors for binary variables such as industry membership. A company either participates in an industry or it does not. The industry factor sensitivities would be 0 – 1 dummy variables; in models that recognize that companies frequently operate in multiple industries, the value of the sensitivity would be 1 for each industry in which a company operated.
432A second distinction between macroeconomic multifactor models and fundamental factor models is that with the former, we develop the factor (surprise) series first and then estimate the factor sensitivities through regressions; with the latter, we generally specify the factor sensitivities (attributes) first and then estimate the factor returns through regressions.
433
4.5. Multifactor Models in Current Practice
In the previous sections, we explained the basic concepts of multifactor models and the APT. We now describe some models in actual industry use.
4.5.1. Macroeconomic Factor Models Chen, Roll, and Ross (1986) pioneered the development of macroeconomic factor models. Following statistically based research suggesting that more than one factor was important in explaining the average returns on U.S. stocks, Chen et al. suggested that a relatively small set of macro factors was the primary influence on the U.S. stock market. The factors in the Chen et al. study were (1) inflation, including unanticipated inflation and changes in expected inflation, (2) a factor related to the term structure of interest rates, represented by long-term government bond returns minus one-month Treasury-bill rates, (3) a factor reflecting changes in market risk and investors’ risk aversion, represented by the difference between the returns on low-rated and high-rated bonds, and (4) changes in industrial production.
The usefulness of any factor for explaining asset returns is generally evaluated using historical data. Our confidence that a factor will explain future returns increases if we can give an economic explanation of why a factor should be important in explaining average returns. We can plausibly explain all of Chen et al.’s four factors. For example, inflation affects the cash flows of businesses as well as the level of the discount rate applied to these cash flows by investors. Changes in industrial production affect the cash flows of businesses and the opportunities faced by investors. Example 11-14 details a current macroeconomic factor model that expanded on the model of Chen et al.
EXAMPLE 11-14 Expected Return in a Macroeconomic Factor Model
Burmeister, Roll, and Ross (1994) presented a macroeconomic factor model to explain the returns on U.S. equities. The model is known as the BIRR model for short. The BIRR model includes five factors:
1. Confidence risk: the unanticipated change in the return difference between risky corporate bonds and government bonds, both with maturities of 20 years. Risky corporate bonds bear greater default risk than does government debt. Investors’ attitudes toward this risk should affect the average returns on equities. To explain the factor’s name, when their confidence is high, investors are willing to accept a smaller reward for bearing this risk.
2. Time horizon risk: the unanticipated change in the return difference between 20-year government bonds and 30-day Treasury bills. This factor reflects investors’ willingness to invest for the long term.
3. Inflation risk: the unexpected change in the inflation rate. Nearly all stocks have negative exposure to this factor, as their returns decline with positive surprises in inflation.
4. Business cycle risk: the unexpected change in the level of real business activity. A positive surprise or unanticipated change indicates that the expected growth rate of the economy, measured in constant dollars, has increased.
5. Market timing risk: the portion of the S&P 500’s total return that remains unexplained by the first four risk factors.
434 Almost all stocks have positive sensitivity to this factor.
The first four factors are quite similar to Chen et al.’s factors with respect to the economic influences they seek to capture. The fifth factor acknowledges the uncertainty surrounding the correct set of underlying variables for asset pricing; this factor captures influences on the returns to the S&P 500 not explained by the first four factors.
The S&P 500 is a widely used index of 500 U.S. stocks of leading companies in leading industries. Burmeister et al. used the S&P 500 to gauge the influence of their five factors on the mean excess returns (above the Treasury bill rate) to the S&P 500.
Table 11-15 shows their results.
TABLE 11-15 Explaining the Annual Expected Excess Return for the S&P 500
Source: Burmeister et al.
The estimated APT model is E(Rp) = T-bill rate + 2.59(Confidence risk) – 0. 66(Time horizon risk) – 4.32(Inflation risk) + 1.49(Business cycle risk) + 3.61 (Market timing risk). The table shows that the S&P 500 had positive exposure to every risk factor except inflation risk. The two largest contributions to excess return came from market timing risk and business cycle risk. According to the table, this model predicts that the S&P 500 will have an expected excess return of 8.09 percent above the T-bill rate. Therefore, if the 30-day Treasury bill rate were 4 percent, for example, the forecasted return for the S&P 500 would be 4 + 8.09 = 12.09 percent a year.
In Example 11-15, we illustrate how we might use the Burmeister et al. factor model to assess the factor bets placed by a portfolio manager managing a U.S. active core equity portfolio (an actively managed portfolio invested in large-cap stocks).
EXAMPLE 11-15 Exposures to Economy-Wide Risks
William Hughes is the portfolio manager of a U.S. core equity portfolio that is being evaluated relative to its benchmark, the S&P 500. Because Hughes’s performance will be evaluated relative to this benchmark, it is useful to understand the active factor bets that Hughes took relative to the S&P 500. With a focus on exposures to economy-wide risk, we use the Burmeister et al. model already presented.
Table 11-16 displays Hughes’s data.
We see that the portfolio manager tracks the S&P 500 exactly on confidence and time horizon risk but tilts toward greater business cycle risk. The portfolio also has a small positive excess exposure to the market timing factor.
We can use the excess exposure to business cycle risk to illustrate the numerical interpretation of the excess sensitivities. Ignoring nonsystematic risk and holding the values of the other factors constant, if there is a +1 percent surprise in the business cycle factor, we expect the return on the portfolio to be 0.01 × 0.54 = 0.0054 or 0.54 percent higher than the return on the S&P 500. Conversely, we expect the return on the portfolio to be lower than the S&P 500’s return by an equal amount for a -1 percent surprise in business cycle risk.
TABLE 11-16 Excess Factor Sensitivities for a Core Equity Portfolio
Because of the excess exposure of 0.54, the portfolio manager appears to be placing a bet on economic expansion, relative to the benchmark. If the factor bet is inadvertent, Hughes is perhaps assuming an unwanted risk. If he is aware of the bet, what are the reasons for the bet?
Care must be taken in interpreting the portfolio manager’s excess sensitivity of 0.25 to the inflation factor. The S&P 500 has a negative inflation factor exposure. The value of 0.25 represents a smaller negative exposure to inflation for the core portfolio—that is, less rather than more exposure to inflation risk. Note from
Table 11-16 that because the risk premium for inflation risk is negative, Hughes is giving up expected return relative to the benchmark by his bet on inflation. Again, what are his reasons for the inflation factor bet?
The market timing factor has an interpretation somewhat similar to that of the CAPM beta about how a stock tends to respond to changes in the broad market, with a higher value indicating higher sensitivity to market returns, all else equal. But the market timing factor reflects only the portion of the S&P 500’s returns not explained by the other four factors, and the two concepts are distinct. Whereas we would expect S&P 500 returns to be correlated with one or more of the first four factors, the market timing factor is constructed to be uncorrelated with the first four factors. Because the market timing factor and the S&P 500 returns are distinct, we would not expect market timing factor sensitivity to be proportional to CAPM beta computed relative to the S&P 500, in general.
Another major macroeconomic factor model is the Salomon Smith Barney U.S. Equity Risk Attribute Model, or Salomon RAM, for short.
EXAMPLE 11-16 Expected Return in the Salomon RAM
The Salomon RAM model explains returns to U.S. stocks in terms of nine factors: six macroeconomic factors, a residual market factor, a residual size factor, and a residual sector factor:
1. Economic growth: the monthly change in industrial production.
2. Credit quality: the monthly change in the yield of the Salomon Smith Barney High-Yield Market 10+ year index, after removing the component of the change that is correlated with the monthly changes in the yields of 30-year Treasury bonds.
3. Long rates: the monthly change in the yield of the 30-year Treasury bond.
4. Short rates: the monthly change in the yield of the 3-month Treasury bill.
5. Inflation shock: the unexpected component of monthly change in the consumer price index (CPI).
6. Dollar: the monthly change in the trade-weighted dollar.
7. Residual market: the monthly return on the S&P 500 after removing the effects of the six factors above.
8. Small-cap premium: the monthly difference between the return on the Russell 2000 Index and the S&P 500, after removing the effect of the seven factors above.
9. Residual sector: the monthly return on a sector membership index after removing the effect of the eight factors above.
Some noteworthy points concerning this model are as follows:
435 • In contrast to the BIRR model and the general model (
Equation 11-16), all the factors except inflation are stated in terms of returns rather than surprises.
• Factors 7, 8, and 9 attempt to isolate the net or unique contribution of the factor by removing the component of the factor return that is correlated with the group of preceding factors. Factors 7, 8, and 9 are each uncorrelated among themselves and with the other factors; they are said to be orthogonal (uncorrelated) factors. In addition, the credit quality factor is constructed to be uncorrelated with the long-rate factor.
• Based on the explanatory power of the model, each stock receives a RAM ranking that reflects its coefficient of determination, with 1 the highest and 5 the lowest rank.
• The factor sensitivities are presented in standardized form.
The bank and the computer manufacturer have investment-grade debt. The cable TV provider and department store are relatively heavy users of debt that is rated below investment grade. The computer manufacturer uses little debt in its capital structure. Based only on the information given, answer the following questions.
1. Contrast the factor sensitivities of the cable TV provider stock to those of the average stock.
2. State which stocks are expected to do well in an economy showing strong economic growth coupled with an improving credit environment, all else equal.
3. Explain a possible business reason or a reason related to company fundamentals to explain negative sensitivity of the cable TV provider’s stock to the credit quality factor.
Solution to 1: The factor sensitivities to short rates, the trade-weighted dollar, the residual market factor, and the small-cap premium factor are above average, as indicated by positive factor sensitivities. The sensitivity to the residual sector factor is average, as indicated by zero factor sensitivity. By contrast, the cable TV provider’s stock has below-average sensitivity to the economic growth, credit quality, long-rate, and inflation factors, as indicated by negative factor sensitivities.
Solution to 2: Both the bank and the computer manufacturer have positive sensitivity to the economic growth factor, which is the monthly change in industrial production. As the factor and factor sensitivity are defined, the positive sensitivity implies above-average returns for these two stocks in an environment of strong economic growth, all else equal. The bank has a negative coefficient on the credit quality factor, whereas the computer manufacturer has a positive sensitivity. An improving credit environment means that the yields of high-yield bonds are declining. Thus we would observe a negative value for the credit quality factor in that environment. Of the two stocks, we expect that only the bank stock with a negative sensitivity should give above-average returns in an improving credit environment. Thus the bank stock is expected to do well in the stated scenario.
Solution to 3: The credit quality factor essentially measures the change in the premium for bearing default risk. A negative coefficient on the credit quality factor means that the stock should do well when the premium for bearing default risk declines (an improving credit environment). One explanation for the negative sensitivity of the cable TV provider’s stock to the credit quality factor is that the company is a heavy borrower with less than investment-grade debt. The cost of such debt reflects a significant default premium. The cable TV provider’s borrowing costs should decline in an improving credit environment; that decline should positively affect its stock price.
4.5.2. Fundamental Factor Models Financial analysts frequently use fundamental factor models for a variety of purposes, including portfolio performance attribution and risk analysis.
436 Fundamental factor models focus on explaining the returns to individual stocks using observable fundamental factors that describe either attributes of the securities themselves or attributes of the securities’ issuers. Industry membership, price-earnings ratio, book value-to-price ratio, size, and financial leverage are examples of fundamental factors.
Example 11-17 reports a study that examined macroeconomic, fundamental, and statistical factor models.
EXAMPLE 11-17 Alternative Factor Models
Connor (1995) contrasted a macroeconomic factor model with a fundamental factor model to compare how well the models explain stock returns.
437Connor reported the results of applying a macroeconomic factor model to the returns for 779 large-cap U.S. stocks based on monthly data from January 1985 through December 1993. Using five macroeconomic factors, Connor was able to explain approximately 11 percent of the variance of return on these stocks.
438 Table 11-18 shows his results.
TABLE 11-18 The Explanatory Power of the Macroeconomic Factors
Source: Connor (1995).
| Factor | Explanatory Power from Using Each Factor Alone | Increase in Explanatory Power from Adding Each Factor to All the Others |
|---|
| Inflation | 1.3% | 0.0% |
| Term structure | 1.1% | 7.7% |
| Industrial production | 0.5% | 0.3% |
| Default premium | 2.4% | 8.1% |
| Unemployment | -0.3% | 0.1% |
| All factors | | 10.9% |
Connor also reported a fundamental factor analysis of the same companies for which he conducted a macroeconomic factor analysis. The factor model employed was the BARRA US-E2 model (the current version is E3).
Table 11-19 shows these results. In the table, “variability in markets” represents the stock’s volatility, “success” is a price momentum variable, “trade activity” distinguishes stocks by how often their shares trade, and “growth” distinguishes stocks by past and anticipated earnings growth.
439TABLE 11-19 The Explanatory Power of the Fundamental Factors
Source: Connor (1995).
| Factor | Explanatory Power from Using Each Factor Alone | Increase in Explanatory Power from Adding Each Factor to All the Others |
|---|
| Industries | 16.3% | 18.0% |
| Variability in markets | 4.3% | 0.9% |
| Success | 2.8% | 0.8% |
| Size | 1.4% | 0.6% |
| Trade activity | 1.4% | 0.5% |
| Growth | 3.0% | 0.4% |
| Earnings to price | 2.2% | 0.6% |
| Book to price | 1.5% | 0.6% |
| Earnings variability | 2.5% | 0.4% |
| Financial leverage | 0.9% | 0.5% |
| Foreign investment | 0.7% | 0.4% |
| Labor intensity | 2.2% | 0.5% |
| Dividend yield | 2.9% | 0.4% |
| All factors | | 42.6% |
As
Table 11-19 shows, the most important fundamental factor is “industries,”
11 represented by 55 industry dummy variables. The fundamental factor model explained approximately 43 percent of the variation in stock returns, compared with approximately 11 percent for the macroeconomic factor model. Connor’s article does not provide tests of the statistical significance of the various factors in either model; however, Connor did find strong evidence for the usefulness of fundamental factor models, and this evidence is mirrored by the wide use of those models in the investment community. Fundamental factor models are frequently used in portfolio performance attribution, for example. We shall illustrate this use later in the chapter. Typically, fundamental factor models employ many more factors than macroeconomic factor models, giving a more detailed picture of the sources of a portfolio manager’s results.
We cannot conclude from this study that fundamental factor models are inherently superior to macroeconomic factors, however. Each of the major types of models has its uses. The factors in various macroeconomic factor models are individually backed by statistical evidence that they represent systematic risk (i.e., risk that cannot be diversified away). In contrast, a portfolio manager can easily construct a portfolio that excludes a particular industry, so exposure to a particular industry is not systematic risk. The two types of factors, macroeconomic and fundamental, have different implications for measuring and managing risk, in general. The macroeconomic factor set is parsimonious (five variables). The fundamental factor set is large (67 variables including the 55 industry dummy variables), and at the expense of greater complexity, it can give a more detailed picture of risk in terms that are easily related to company and security characteristics. Connor found that the macroeconomic factor model had no marginal explanatory power when added to the fundamental factor model, implying that the fundamental risk attributes capture all the risk characteristics represented by the macroeconomic factor betas. Because the fundamental factors supply such a detailed description of the characteristics of a stock and its issuer, however, this finding is not necessarily surprising.
We encounter a range of distinct representations of risk in the fundamental models that are currently used in practical applications. Diversity exists in both the identity and exact definition of factors as well as in the underlying functional form and estimation procedures. Despite the diversity, we can place the factors of most fundamental factor models for equities into three broad groups:
• Company fundamental factors. These are factors related to the company’s internal performance. Examples are factors relating to earnings growth, earnings variability, earnings momentum, and financial leverage.
• Company share-related factors. These factors include valuation measures and other factors related to share price or the trading characteristics of the shares. In contrast to the previous category, these factors directly incorporate investors’ expectations concerning the company. Examples include price multiples such as earnings yield, dividend yield, and book-to-market. Market capitalization falls under this heading. Various models incorporate variables relating to share price momentum, share price volatility, and trading activity that fall in this category.
• Macroeconomic factors. Sector or industry membership factors come under this heading. Various models include factors such as CAPM beta, other similar measures of systematic risk, and yield curve level sensitivity, all of which can be placed in this category.
4.6. Applications
The following sections present some of the major applications of multifactor models in investment practice.
We begin by discussing portfolio performance attribution and risk analysis. We could frame the discussion in terms of raw returns or in terms of returns relative to a portfolio’s benchmark. Because they provide a reference standard for risk and return, benchmarks play an important role in many institutional investors’ plans for quantitatively risk-controlled returns. We shall thus focus on analyzing returns relative to a benchmark.
Multifactor models can also help portfolio managers form portfolios with specific desired risk characteristics. After discussing performance attribution and risk analysis, we explain the use of multifactor models in creating a portfolio with risk exposures that are similar to those of another portfolio.
4.6.1. Analyzing Sources of Returns Multifactor models can help us understand in detail the sources of a manager’s returns relative to a benchmark. For simplicity, in this section we analyze the sources of the returns of a portfolio fully invested in the equities of a single national equity market.
440Analysts frequently favor fundamental multifactor models in decomposing (separating into basic elements) the sources of returns. In contrast to statistical factor models, fundamental factor models allow the sources of portfolio performance to be described by name. Also, in contrast to macroeconomic factor models, fundamental models suggest investment style choices and security characteristics more directly, and often in greater detail.
We first need to understand the objectives of active managers. As mentioned, managers are commonly evaluated relative to a specified benchmark. Active portfolio managers hold securities in different-from-benchmark weights in an attempt to add value to their portfolios relative to a passive investment approach. Securities held in different-from-benchmark weights reflect portfolio manager expectations that differ from consensus expectations. For an equity manager, those expectations may relate to common factors driving equity returns or to considerations unique to a company. Thus when we evaluate an active manager, we want to ask questions such as “Did the manager have insights that were valuable in the sense of adding value above a passive strategy?” Analyzing the sources of returns using multifactor models can help answer these questions.
The return on a portfolio,
Rp, can be viewed as the sum of the benchmark’s return,
RB, and the
active return (portfolio return minus benchmark return):
(11-20)
With a factor model in hand, we can analyze a portfolio manager’s active return as the sum of two components. The first component is the product of portfolio manager’s factor tilts (active factor sensitivities) and the factor returns; we may call that component the return from factor tilts. The second component is the part of active return reflecting the manager’s skill in individual asset selection; we may call that component asset selection.
Equation 11-21 shows the decomposition of active return into those two components:
In
Equation 11-21, we measure the portfolio’s and benchmark’s sensitivities to each factor in our risk model at the beginning of an evaluation period.
Example 11-18 illustrates the use of a relatively parsimonious fundamental factor model in decomposing and interpreting returns.
EXAMPLE 11-18 Active Return Decomposition of an Equity Portfolio Manager
As an equity analyst at a pension fund sponsor, Ronald Service uses the following multifactor model to evaluate U.S. equity portfolios:
where
Rp and RF = the return on the portfolio and the risk-free rate of return, respectively
RMRF = the return on a value-weighted equity index in excess of the one-month T-bill rate
SMB = small minus big, a size (market capitalization) factor. SMB is the average return on three small-cap portfolios minus the average return on three large-cap portfolios.
HML = high minus low, the average return on two high book-to-market portfolios minus the average return on two low book-to-market portfolios
WML = winners minus losers, a momentum factor. WML is the return on a portfolio of the past year’s winners minus the return on a portfolio of the past year’s losers.
441In
Equation 11-22, the sensitivities are interpreted as regression coefficients and are not standardized.
Service’s current task is evaluating the performance of the most recently hired U.S. equity manager. That manager’s benchmark is the Russell 1000, an index representing the performance of U.S. large-cap stocks. The manager describes herself as a “stock picker” and points to her performance in beating the benchmark as evidence that she is successful.
Table 11-20 presents an analysis based on
Equation 11-21 of the sources of that manager’s active return during the year. In
Table 11-20, “A. Return from Factor Tilts,” equal to 2.1241 percent, sums the four numbers above it in the column; the return from factor tilts is the first component of the
Equation 11-21.
Table 11-20 lists asset selection as equal to -0.05 percent. Active return is found as 2.1241% + (-0.05%) = 2.0741%.
From his previous work, Service knows that the returns to growth-style portfolios often have a positive sensitivity to the momentum factor (WML) in
Equation 11-22. By contrast, the returns to certain value-style portfolios, such as those following a contrarian strategy, often have low or negative sensitivity to the momentum factor.
Using the information given, address the following:
1. Determine the manager’s investment style mandate.
2. Evaluate the sources of the manager’s active return for the year.
3. What concerns might Service discuss with the manager as a result of the return decomposition?
Solution to 1: The benchmark’s sensitivities reflect the baseline risk characteristics of a manager’s investment opportunity set. We can infer the manager’s anticipated style by examining the characteristics of the benchmark selected for her. We then confirm these inferences by examining the portfolio’s actual factor exposures:
• Stocks with high book-to-market are generally viewed as value stocks. Because the pension sponsor selected a benchmark with a high sensitivity (1.0) to HML (the high book-to-market minus low book-to-market factor), we can infer that the manager has a value orientation. The actual sensitivity of 1.4 to HML indicates that the manager had even more exposure to high book-to-market stocks than the benchmark.
• The benchmark’s and portfolio’s approximate neutrality to the momentum factor is consistent with a value orientation.
• The benchmark’s and portfolio’s low exposure to SMB suggests essentially no net exposure to small-cap stocks.
The above considerations as a group suggest that the manager has a large-cap value orientation.
Solution to 2: The dominant source of the manager’s positive active return was her positive active exposure to the HML factor. The bet contributed (1.40 – 1.00)(5.10%) = 2.04% or approximately 98 percent of the realized active return of about 2.07 percent. During the evaluation period, the manager sharpened her value orientation, and that bet paid off. The manager’s active exposure to the overall market (RMRF) was unprofitable, but her active exposures to small stocks (SMB) and to momentum (WML) were profitable; however, the magnitudes of the manager’s active exposures to RMRF, SMB, and WML were relatively small, so the effects of those bets on active return was minor compared with her large and successful bet on HML.
Solution to 3: Although the manager is a self-described “stock picker,” her active return from asset selection in this period was actually negative. Her positive active return resulted from the concurrence of a large active bet on HML and a high return to that factor during the period. If the market had favored growth rather than value without the manager doing better in individual asset selection, the manager’s performance would have been unsatisfactory. Can the manager supply evidence that she can predict changes in returns to the HML factor? Is she overconfident about her stock selection ability? Service may want to discuss these concerns with the manager. The return decomposition has helped Service distinguish between the return from positioning along the value-growth spectrum and return from insights into individual stocks within the investment approach the manager has chosen.
4.6.2. Analyzing Sources of Risk Continuing with our focus on active returns, in this section we explore analysis of active risk.
Active risk is the standard deviation of active returns. Many terms in use refer to exactly the same concept, so we need to take a short detour to mention them. A traditional synonym is
tracking error (TE), but the term may be confusing unless
error is associated by the reader with
standard deviation; tracking-error volatility (TEV) has been used (where
error is understood as a
difference); and
tracking risk is now in common use (but the natural abbreviation TR could be misunderstood to refer to total return). We will use the abbreviation TE for the concept of tracking risk, and we will refer to it usually as tracking risk:
In
Equation 11-23,
s(
Rp —RB) indicates that we take the sample standard deviation (indicated by
s) of the time series of differences between the portfolio return,
Rp, and the benchmark return,
RB. We should be careful that active return and tracking risk are stated on the same time basis.
442As a broad indication of ranges for tracking risk, in U.S. equity markets a well executed passive investment strategy can often achieve tracking risk on the order of 1 percent or less per annum. A semi-active or enhanced index investment strategy, which makes tightly controlled use of managers’ expectations, often has a tracking risk goal of 2 percent per annum. A diversified active U.S. large-cap equity strategy that might be benchmarked on the S&P 500 would commonly have tracking risk in the range of 2 percent to 6 percent per annum. An aggressive active equity manager might have tracking risk in the range of 6 percent to 9 percent or more.
Somewhat analogous to use of the traditional Sharpe measure in evaluating absolute returns, the ratio of mean active return to active risk, the
information ratio (IR), is a tool for evaluating mean active returns per unit of active risk. The historical or
ex post IR has the form
In the numerator of
Equation 11-24,

and

stand for the sample mean return on the portfolio and the sample mean return on the benchmark, respectively. To illustrate the calculation, if a portfolio achieved a mean return of 9 percent during the same period that its benchmark earned a mean return of 7.5 percent, and the portfolio’s tracking risk was 6 percent, we would calculate an information ratio of (9%—7.5%)/6% = 0.25. Setting guidelines for acceptable active risk or tracking risk is one of the ways that some institutional investors attempt to assure that the overall risk and style characteristics of their investments are in line with those desired.
EXAMPLE 11-19 Communicating with Investment Managers
The framework of active return and active risk is appealing to investors who want to closely control the risk of investments. The benchmark serves as a known and continuously observable reference standard in relation to which quantitative risk and return objectives may be stated and communicated. For example, a U.S. public employee retirement system issued a solicitation (or request for proposal) to prospective investment managers for a “risk-controlled U.S. large-cap equity fund” that included the following requirements:
• Shares must be components of the S&P 500.
• The portfolio should have a minimum of 200 issues. At time of purchase, the maximum amount that may be invested in any one issuer is 5 percent of the portfolio at market value or 150 percent of the issuers’ weight within the S&P 500 Index, whichever is greater.
• The portfolio must have a minimum 0.30 percent information ratio either since inception or over the last seven years.
• The portfolio must also have tracking risk of less than 4.0 percent with respect to the S&P 500 either since inception or over the last seven years.
Analysts use multifactor models to understand in detail a portfolio manager’s risk exposures. In decomposing active risk, the analyst’s objective is to measure the portfolio’s active exposure along each dimension of risk—in other words, to understand the sources of tracking risk.
443 Among the questions analysts will want to answer are the following:
• What active exposures contributed most to the manager’s tracking risk?
• Was the portfolio manager aware of the nature of his active exposures, and if so, can he articulate a rationale for assuming them?
• Are the portfolio’s active risk exposures consistent with the manager’s stated investment philosophy?
• Which active bets earned adequate returns for the level of active risk taken?
In addressing these questions, analysts often choose fundamental factor models because they can be used to relate active risk exposures to a manager’s portfolio decisions in a fairly direct and intuitive way. In this section, we explain how to decompose or explain a portfolio’s active risk using a multifactor model.
We previously addressed the decomposition of active return; now we address the decomposition of active risk. In analyzing risk, it is convenient to use variances rather than standard deviations because the variances of uncorrelated variables are additive. We refer to the variance of active risk as
active risk squared:
(11-25)
We can separate a portfolio’s active risk squared into two components:
•
Active factor risk is the contribution to active risk squared resulting from the portfolio’s different-than-benchmark exposures relative to factors specified in the risk model.
444 •
Active specific risk or
asset selection risk is the contribution to active risk squared resulting from the portfolio’s active weights on individual assets as those weights interact with assets’ residual risk.
445 When applied to an investment in a single asset class, active risk squared has two components. The decomposition of active risk squared into two components is
Active factor risk represents the part of active risk squared explained by the portfolio active factor exposures. Active factor risk can be found indirectly as the difference between active risk squared and active specific risk, which has the expression
446
where

is the
ith asset’s active weight in the portfolio (that is, the difference between the asset’s weight in the portfolio and its weight in the benchmark) and

is the residual risk of the
ith asset (the variance of the
ith asset’s returns left unexplained by the factors).
447 Active specific risk identifies the active nonfactor or residual risk assumed by the manager. We should look for a positive average return from asset selection as compensation for bearing active specific risk.
EXAMPLE 11-20 A Comparison of Active Risk
Richard Gray is comparing the risk of four U.S. equity managers who share the same benchmark. He uses a fundamental factor model, the BARRA US-E3 model, which incorporates 13 risk indexes and a set of 52 industrial categories. The risk indexes measure various fundamental aspects of companies and their shares such as size, leverage, and dividend yield. In the model, companies have nonzero exposures to all industries in which the company operates.
Table 11-21 presents Gray’s analysis of the active risk squared of the four managers, based on
Equation 11-26.
448 In
Table 11-21, the column labeled “Industry” gives the portfolio’s active factor risk associated with the industry exposures of its holdings; the column “Risk Indexes” gives the portfolio’s active factor risk associated with the exposures of its holdings to the 13 risk indexes.
Using the information in
Table 11-21, address the following:
1. Contrast the active risk decomposition of Portfolios A and B.
2. Contrast the active risk decomposition of Portfolios B and C.
3. Characterize the investment approach of Portfolio D.
Solution to 1:
Table 11-22 restates the information in
Table 11-21 to show the proportional contributions of the various sources of active risk. In the last column of
Table 11-22, we now give the square root of active risk squared—that is, active risk or tracking risk. To explain the middle set of columns in
Table 11-22, Portfolio A’s value of 25 percent under the Industry column is found as 12.25/49 = 0.25. So Portfolio A’s active risk related to industry exposures is 25 percent of active risk squared.
Portfolio A has assumed a higher level of active risk than B (tracking risk of 7 percent versus 5 percent). Portfolios A and B assumed the same proportions of active factor and active specific risk, but a sharp contrast exists between the two in terms of type of active factor risk exposure. Portfolio A assumed substantial active industry risk, whereas Portfolio B was approximately industry neutral relative to the benchmark. By contrast, Portfolio B had higher active bets on the risk indexes representing company and share characteristics.
Solution to 2: Portfolios B and C were similar in their absolute amounts of active risk. Furthermore, both Portfolios B and C were both approximately industry neutral relative to the benchmark. Portfolio C assumed more active factor risk related to the risk indexes, but B assumed more active specific risk. We can also infer from the second point that B is somewhat less diversified than C.
Solution to 3: Portfolio D appears to be a passively managed portfolio, judging by its negligible level of active risk. Referring to
Table 11-21, Portfolio D’s active factor risk of 0.50, equal to 0.707 percent expressed as a standard deviation, indicates that the portfolio very closely matches the benchmark along the dimensions of risk that the model identifies as driving average returns.
Example 11-20 presented a set of hypothetical portfolios with differing degrees of tracking risk in which active factor risk tended to be larger than active specific risk. Given a well-constructed multifactor model and a well-diversified portfolio, this relationship is fairly commonplace. For well-diversified portfolios, managing active factor risk is typically the chief task in managing tracking risk.
Example 11-20 presented an analysis of active risk at an aggregated level; a portfolio’s active factor risks with respect to the multifactor model’s 13 risk indexes was aggregated into a single number. In appraising performance, an analyst may be interested in a much more detailed analysis of a portfolio’s active risk. How can an analyst appraise the individual contributions of a manager’s active factor exposures to active risk squared?
Whatever the set of factors, the procedure for evaluating the contribution of an active factor exposure to active risk squared is the same. This quantity has been called a factor’s marginal contribution to active risk squared (FMCAR). With
K factors, the marginal contribution to active risk squared for a factor
j, FMCAR
j is
where
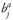
is the portfolio’s active exposure to factor
j. The numerator is the active factor risk for factor
j.
449 The numerator is similar to expressions involving beta that we encountered earlier in discussing the market model, but with multiple factors, factor covariances as well as variances are relevant. To illustrate
Equation 11-27 in a simple setting, suppose we have a two-factor model:
• The manager’s active exposure to the first factor is 0.50; that is,

. The other active factor exposure is
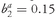
.
• The variance-covariance matrix of the factors is described by Cov(F1, F1) = σ2(F1) = 225, Cov(F1, F2) = 12, and Cov(F2, F2) = σ2(F2) = 144.
• Active specific risk is 53.71.
We first compute active factor risk for each factor; that calculation is the numerator in
Equation 11-27. Then we find active risk squared by summing the active factor risks and active specific risk, and form the ratio indicated in
Equation 11-27. For the first factor, we calculate the numerator of FMCAR
1 as
For the second factor, we have
Active factor risk is 57.15 + 4.14 = 61.29. Adding active specific risk, we find that active risk squared is 61.29 + 53.71 = 115. Thus we have FMCAR1 = 57.15/115 = 0.497 or 49.7 percent, and FMCAR2 = 4.14/115 = 0.036 or 3.6 percent. Active factor risk as a fraction of total risk is FMCAR1 + FMCAR2 = 49.7% + 3.6% = 53.3%. Active specific risk contributes 100%—53.3% = 46.7% to active risk squared. Example 11-21 illustrates the application of these concepts.
EXAMPLE 11-21 An Analysis of Individual Active Factor Risk
William Whetzell is responsible for a monthly internal performance attribution and risk analysis of a domestic core equity fund managed internally by his organization, a Canadian endowment. In his monthly analyses, Whetzell uses a risk model incorporating the following factors:
• Log of market cap
• E/P, the earnings yield
• B/P, the book-to-price ratio
• Earnings growth
• Average dividend yield
• D/A, the long-term debt-to-asset ratio
• Volatility of return on equity (ROE)
• Volatility of EPS
The factor sensitivities in the model have the standard interpretation of factor sensitivities in fundamental factor models.
Having determined that he earned an active return of 0.75 percent during the last fiscal year, Whetzell turns to the task of analyzing the portfolio’s risk. At the start of that fiscal year, the investment committee made the following decisions:
• to tactically tilt the portfolio in the direction of small-cap stocks;
• to implement an “earnings growth at a reasonable price” (GARP) bias in security selection;
• to keep any active factor risk, expressed as a standard deviation, under 5 percent per annum;
• to keep active specific risk at no more than 50 percent of active risk squared; and
• to achieve an information ratio of 0.15 or greater.
Before Whetzell presented his report, one investment committee member reviewing his material commented that the investment committee should adopt a passive investment strategy for domestic equities if the equity fund continues to perform as it did during the last fiscal year.
Table 11-23 presents information on the equity fund. The factor returns were constructed to be approximately mutually uncorrelated.
Based on the information in
Table 11-23, address the following:
1. For each factor, calculate (A) the active factor risk and (B) the marginal contribution to active risk squared.
2. Discuss whether the data are consistent with the objectives of the investment committee having been met.
3. Appraise the endowment’s risk-adjusted performance for the year.
4. Explain two pieces of evidence supporting the committee member’s statement concerning a passive investment strategy.
Solution to 1:
a. Active factor risk for a factor = (Active sensitivity to the factor)
2(Factor variance) in
Equation 11-27 with zero factor correlations.
Log of market cap = (0.05—0.25)2 (225) = 9.0
E/P = (—0.05—0.05)2(144) = 1.44
B/P = [—0.25—(—0.02)]2(100) = 5.29
Earnings growth = (0.25—0.10)2 (196) = 4.41
Dividend yield = (0.01—0.00)2 (169) = 0.0169
D/A = (0.03—0.03)2(81) = 0.0
Volatility of ROE = (—0.25—0.02)2(121) = 8.8209
Volatility of EPS = (—0.10—0.03)2 (64) = 1.0816
b. The sum of the individual active factor risks equals 30.0594. We add active specific risk to this sum to obtain active risk squared of 30.0594 + 29.9406 = 60. Thus FMCAR for the factors is as follows:
Log of market cap = 9/60 = 0.15
E/P = 1.44/60 = 0.024
B/P = 5.29/60 = 0.0882
Earnings growth = 4.41/60 = 0.0735
Dividend yield = 0.0169/60 = 0.0003
D/A = 0.0/60 = 0.0
Volatility of ROE = 8.8209/60 = 0.1470
Volatility of EPS = 1.0816/60 = 0.0180
Solution to 2: We consider each investment committee objective in turn. The first objective was to tactically tilt the portfolio in the direction of small-cap stocks. A zero sensitivity to the log market cap factor would indicate average exposure to size. An exposure of 1 would indicate a positive exposure to returns to increasing size that is one standard deviation above the mean, given the standard interpretation of factor sensitivities in fundamental factor models. Although the equity fund’s exposure to size is positive, the active exposure is negative. This result is consistent with tilting toward small-cap stocks.
The second objective was to implement an “earnings growth at a reasonable price” bias in security selection. The equity fund has a positive active exposure to earnings growth consistent with seeking companies with high earnings growth rates. It is questionable, however, whether the “reasonable price” part of the approach is being satisfied. The fund’s absolute E/P and B/P sensitivities are negative, indicating below average earning yield and B/P (higher than average P/E and P/B). The active exposures to these factors are also negative. If above-average earnings growth is priced in the marketplace, the fund may need to bear negative active exposures, so we cannot reach a final conclusion. We can say, however, that none of the data positively supports a conclusion that the GARP strategy was implemented.
The third objective was to keep any active factor risk, expressed as a standard deviation, under 5 percent per annum. The largest active factor risk was on the log of market cap factor. Expressed as a standard deviation, that risk was (9)1/2 = 3 percent per annum, so this objective was met.
The fourth objective was to keep active specific risk at no more than 50 percent of active risk squared. Active specific risk as a fraction of active risk squared was 29.9406/60 = 0.4990 or 49.9 percent, so this objective was met.
The fifth objective was to achieve an information ratio of 0.15 or greater. The information ratio is active return divided by active risk (tracking risk). Active return was given as 0.75 percent. Active risk is the square root of active risk squared: (60)1/2 = 7.7460%. Thus IR = 0.75%/7.7460% = 0.0968 or approximately 0.10, which is short of the stated objective of 0.15.
Solution to 3: The endowment’s realized information ratio of 0.10 means its risk-adjusted performance for the year was inadequate.
Solution to 4: The active specific return for the year was negative, although the fund incurred substantial active specific risk. Therefore, specific risk had a negative reward. Furthermore, the realized information ratio fell short of the investment committee’s objective. With the qualification that this analysis is based on only one year, these facts would argue for the cost-efficient alternative of indexing.
In our discussion of performance attribution and risk analysis, we have given examples related to common stock. Multifactor models have also been used in similar roles for portfolios of bonds and other asset classes.
We have illustrated the use of multifactor models in analyzing a portfolio’s active returns and active risk. At least equally important is the use of multifactor models in portfolio construction. At that stage of the portfolio management process, multifactor models permit the portfolio manager to make focused bets or to control portfolio risk relative to her benchmark’s risk. In the remaining sections, we discuss these uses of multifactor models.
4.6.3. Factor Portfolios A portfolio manager can use multifactor models to establish a specific desired risk profile for his portfolio. For example, he may want to create and use a factor portfolio. A factor portfolio for a particular factor has a sensitivity of 1 for that factor and a sensitivity of 0 for all other factors. It is thus a portfolio with exposure to only one risk factor and exactly represents the risk of that factor. As a pure bet on a source of risk, factor portfolios are of interest to a portfolio manager who wants to hedge that risk (offset it) or speculate on it. Example 11-22 illustrates the use of factor portfolios.
EXAMPLE 11-22 Factor Portfolios
Analyst Wanda Smithfield has constructed six portfolios for possible use by portfolio managers in her firm. The portfolios are labeled A, B, C, D, E, and F in
Table 11-24.
1. A portfolio manager wants to place a bet that real business activity will increase.
a. Determine and justify the portfolio among the six given that would be most useful to the manager.
b. What type of position would the manager take in the portfolio chosen in Part A?
2. A portfolio manager wants to hedge an existing positive exposure to time horizon risk.
a. Determine and justify the portfolio among the six given that would be most useful to the manager.
b. What type of position would the manager take in the portfolio chosen in Part A?
Solution to 1A: Portfolio B is the most appropriate choice. Portfolio B is the factor portfolio for business cycle risk because it has a sensitivity of 1 to business cycle risk and a sensitivity of 0 to all other risk factors. Portfolio B is thus efficient for placing a pure bet on an increase in real business activity.
Solution to 1B: The manager would take a long position in Portfolio B to place a bet on an increase in real business activity.
Solution to 2A: Portfolio D is the appropriate choice. Portfolio D is the factor portfolio for time horizon risk because it has a sensitivity of 1 to time horizon risk and a sensitivity of 0 to all other risk factors. Portfolio D is thus efficient for hedging an existing positive exposure to time horizon risk.
Solution to 2B: The manager would take a short position in Portfolio D to hedge the positive exposure to time horizon risk.
The next section illustrates the procedure for constructing a portfolio with a desired configuration of factor sensitivities.
4.6.4. Creating a Tracking Portfolio In the previous section, we discussed the use of multifactor models to speculate on or hedge a specific factor risk. Perhaps even more commonly, portfolio managers use multifactor models to control the risk of portfolios relative to their benchmarks. For example, in a risk-controlled active or enhanced index strategy, the portfolio manager may attempt to earn a small incremental return relative to her benchmark while controlling risk by matching the factor sensitivities of her portfolio to her benchmark. That portfolio would be an example of a tracking portfolio. A tracking portfolio is a portfolio having factor sensitivities that are matched to those of a benchmark or other portfolio.
The technique of constructing a portfolio with a target set of factor sensitivities involves the solution of a system of equations using algebra.
• Count the number of constraints. Each target value of beta represents a constraint on the portfolio, and another constraint is that the weights of the investments in the portfolio must sum to one. As many investments are needed as there are constraints.
• Set up an equation for the weights of the portfolio’s investments reflecting each constraint on the portfolio. We have an equation stating that the portfolio weights sum to 1. We have an equation for each target factor sensitivity; on the left-hand side of the equal sign, we have a weighted average of the factor sensitivities of the investments to the factor, and on the right-hand side of the equal sign we have the target factor sensitivity.
• Solve the system of equations for the weights of the investments in the portfolio.
In Example 11-23, we illustrate how a tracking portfolio can be created.
EXAMPLE 11-23 Creating a Tracking Portfolio
Suppose that a pension plan sponsor wants to be fully invested in U.S. common stocks. The plan sponsor has specified an equity benchmark for a portfolio manager, who has decided to create a tracking portfolio for the benchmark. For the sake of using familiar data, let us continue with the three portfolios J, K, and L, as well as the same two-factor model from Example 11-13.
The portfolio manager determines that the benchmark has a sensitivity of 1.3 to the surprise in inflation and a sensitivity of 1.975 to the surprise in GDP. There are three constraints. One constraint is that portfolio weights sum to 1, a second is that the weighted sum of sensitivities to the inflation factor equals 1.3 (to match the benchmark), and a third is that the weighted sum of sensitivities to the GDP factor equals 1.975 (to match the benchmark). Thus we need three investments to form the portfolio, which we take to be Portfolios J, K, and L. We repeat
Table 11-14 below.
TABLE 11-14 (repeated) Sample Portfolios for a Two-Factor Model
As mentioned, we need three equations to determine the portfolio weights wJ, wK, and wL in the tracking portfolio.
•
Equation 1. This equation states that portfolio weights must sum to 1.
•
Equation 2. The second equation states that the weighted average of the sensitivities of J, K, and L to the surprise in inflation must equal the benchmark’s sensitivity to the surprise in inflation, 1.3. This requirement ensures that the tracking portfolio has the same inflation risk as the benchmark.
1.0wJ + 0.5wK + 1.3wL = 1.3
•
Equation 3. The third equation states that the weighted average of the sensitivities of J, K, and L to the surprise in GDP must equal the benchmark’s sensitivity to the surprise in GDP, 1.975. This requirement ensures that the tracking portfolio has the same GDP risk as the benchmark.
1.5wJ + 1.0wK + 1.1wL = 1.975
We can solve for the weights as follows. From Equation 1,
wL = (1—
wJ—
wK). We substitute this result in the other two equations to find
1.0wJ + 0.5wK + 1.3(1—wJ—wK) = 1.3, simplifying to wK =—0.375wJ
and
We next substitute wK =—0.375wJ into 0.4wJ—0.1wK = 0.875, obtaining 0.4wJ—0.1 (—0.375wJ) = 0.875 or 0.4wJ +0.0375wJ = 0.875, so wJ = 2.
Using
wK =—0.375
wJ obtained earlier,
wK =—0.375 ×2 =—0.75. Finally, from
wL = (1—
wJ—
wK) = [1—2—(—0.75)] =—0.25. To summarize,
The tracking portfolio has an expected return of 0.14wJ + 0.12wK + 0.11wL = 0.14(2)+(0.12)(—0.75)+01.1(—0.25) = 0.28—0.09—0.0275 = 0.1625. In Example 11-13 using the same inputs, we calculated the APT model as E(Rp) = 0.07—0.02βp,1 + 0.06βp,2. For the tracking portfolio, βp,1 = 1.3 and βp,2 = 1.975. As E(Rp) = 0.07—0.02(1.3) + 0.06(1.975) = 0.1625, we have confirmed the expected return calculation.
4.7. Concluding Remarks
In earlier sections, we showed how models with multiple factors can help portfolio managers solve practical tasks in measuring and controlling risk. We now draw contrasts between the CAPM and the APT, providing additional insight into why some risks may be priced and how, as a result, the portfolio implications of a multifactor world differ from those of the world described by the CAPM. An investor may be able to make better portfolio decisions with a multifactor model than with a single-factor model.
The CAPM provides investors with useful and influential concepts for thinking about investments. Considerable evidence has accumulated, however, that shows that the CAPM provides an incomplete description of risk.
450 What is the portfolio advice of CAPM, and how can we improve on it when more than one source of systematic risk drives asset returns? An investor who believes that the CAPM explains asset returns would hold a portfolio consisting only of the risk-free asset and the market portfolio of risky assets. If the investor had a high tolerance for risk, she would put a greater proportion in the market portfolio. But to the extent the investor held risky assets, she would hold them in amounts proportional to their market-value weights, without consideration for any other dimension of risk. In reality, of course, not everyone holds the same portfolio of risky assets. Practically speaking, this CAPM-oriented investor might hold a money market fund and a portfolio indexed on a broad market index.
451With more than one source of systematic risk, the average investor might still want to hold a broadly based portfolio and the risk-free asset. Other investors, however, may find it appropriate to tilt away from an index fund after considering dimensions of risk ignored by the CAPM. To make this argument, let us explore why, for example, the business cycle is a source of systematic risk, as in the Burmeister et al. model discussed earlier. There is an economic intuition for why this risk is systematic:
452 Most investors hold jobs and are thus sensitive to recessions. Suppose, for example, that a working investor faces the risk of a recession. If this investor compared two stocks with the same CAPM beta, given his concern about recession risk, he would accept a lower return from the counter cyclical stock and require a risk premium on the procyclical one. In contrast, an investor with independent wealth and no job-loss concerns would be willing to accept the recession risk.
If the average investor holding a job bids up the price of the counter cyclical stocks, then recession risk will be priced. In addition, procyclical stocks would have lower prices than if the recession factor were not priced. Investors can thus, as Cochrane (1999a) notes, “earn a substantial premium for holding dimensions of risk unrelated to market movements.”
This view of risk has portfolio implications. The average investor is exposed to and negatively affected by cyclical risk, which is a priced factor. (Risks that do not affect the average investor should not be priced.) Investors who hold jobs (and thus receive labor income) want lower cyclical risk and create a cyclical risk premium, whereas investors without labor income will accept more cyclical risk to capture a premium for a risk that they do not care about. As a result, an investor who faces lower-than-average recession risk optimally tilts towards greater-than-average exposure to the business cycle factor, all else equal.
In summary, investors should know which priced risks they face and analyze the extent of their exposure. Compared with single-factor models, multifactor models offer a rich context for investors to search for ways to improve portfolio selection.

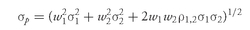

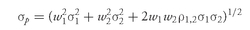
 .
.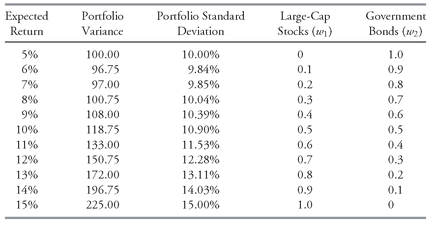
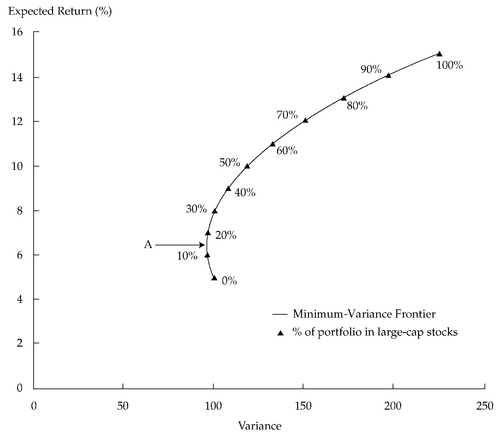








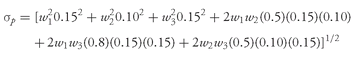
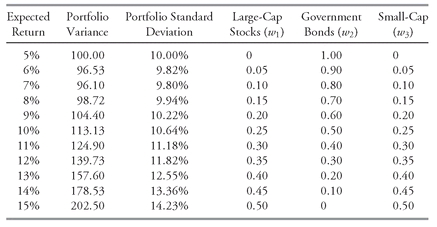
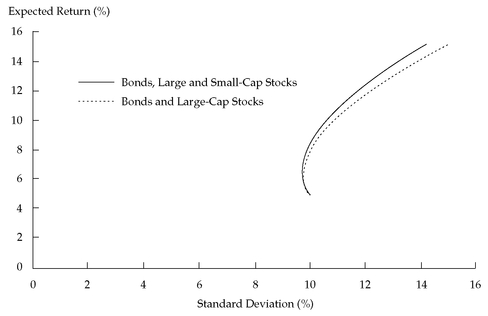

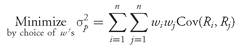
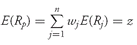 and subject to
and subject to 



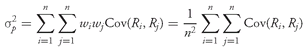
 and the average covariance between all pairs of two stocks
and the average covariance between all pairs of two stocks 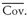 . It is possible to show390 that Equation 11-4 simplifies to
. It is possible to show390 that Equation 11-4 simplifies to

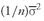 has a limit of 0 as n becomes large. Also, the contribution of the average covariance across stocks to the portfolio variance stays nonzero because
has a limit of 0 as n becomes large. Also, the contribution of the average covariance across stocks to the portfolio variance stays nonzero because  has a limit of
has a limit of 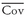 as n becomes large. Therefore, as the number of assets in the portfolio becomes large, portfolio variance approximately equals average covariance. In large portfolios, average covariance—capturing how assets move together—becomes more important than average individual risk or variance.
as n becomes large. Therefore, as the number of assets in the portfolio becomes large, portfolio variance approximately equals average covariance. In large portfolios, average covariance—capturing how assets move together—becomes more important than average individual risk or variance. (using our assumption that all stocks have the same standard deviation of returns, denoted σ).
(using our assumption that all stocks have the same standard deviation of returns, denoted σ). with 0.30σ2:
with 0.30σ2:
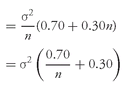
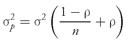
 when n is extremely large. With only 30 stocks, for example, the portfolio variance is only approximately 8 percent larger than minimum possible value (0.323σ2/0.30σ2—1 = 0.077), and the variance is 67.7 percent smaller than the variance of a portfolio that contains only one stock.
when n is extremely large. With only 30 stocks, for example, the portfolio variance is only approximately 8 percent larger than minimum possible value (0.323σ2/0.30σ2—1 = 0.077), and the variance is 67.7 percent smaller than the variance of a portfolio that contains only one stock.

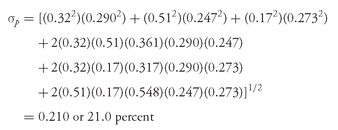

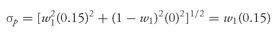
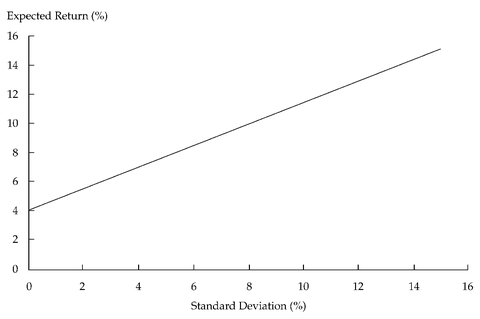

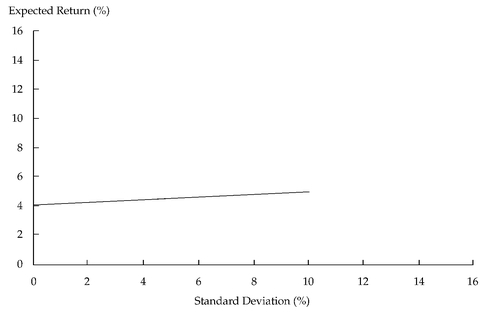
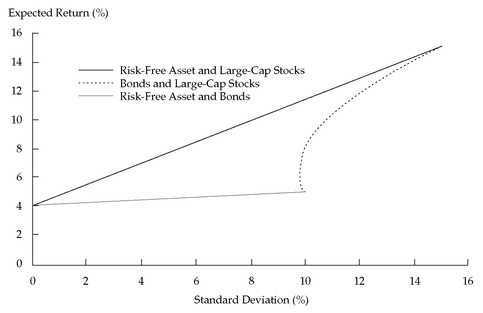



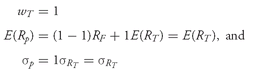
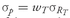 .
.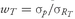 . If we substitute this value of wT back into the expression for expected return, E(Rp)= (1—wT )RF + wT E(RT), we get
. If we substitute this value of wT back into the expression for expected return, E(Rp)= (1—wT )RF + wT E(RT), we get
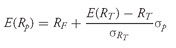
 is the return that the investor demands in order to take on an extra unit of risk. Example 11-5B illustrates how to calculate the investor’s price of risk and other aspects of his investment using the capital allocation line.
is the return that the investor demands in order to take on an extra unit of risk. Example 11-5B illustrates how to calculate the investor’s price of risk and other aspects of his investment using the capital allocation line. . The investor demands an additional 40 basis points of expected return of the portfolio for every 1 percentage point increase in the standard deviation of portfolio returns.
. The investor demands an additional 40 basis points of expected return of the portfolio for every 1 percentage point increase in the standard deviation of portfolio returns. , or 40 percent. In other words, 40 percent of the assets are in the tangency portfolio and 60 percent are in the risk-free asset. The expected return for the portfolio is
, or 40 percent. In other words, 40 percent of the assets are in the tangency portfolio and 60 percent are in the risk-free asset. The expected return for the portfolio is 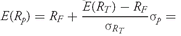
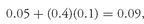 , or 9 percent.
, or 9 percent.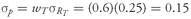 or 15 percent.
or 15 percent.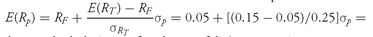
 . If the standard deviation for the portfolio’s returns is 35 percent, then the investor can demand an expected return of E(Rp) = 0.05 + 0.4σp = 0.05 + 0.4(0.35) = 0.19, or 19 percent.
. If the standard deviation for the portfolio’s returns is 35 percent, then the investor can demand an expected return of E(Rp) = 0.05 + 0.4σp = 0.05 + 0.4(0.35) = 0.19, or 19 percent.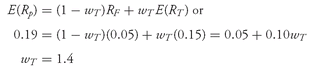




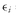 = an error term
= an error term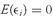 .
. .
. for all i not equal to j.413
for all i not equal to j.413 
 , the variance of the error for the return of asset i in the market model,
, the variance of the error for the return of asset i in the market model, 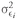 , and the sensitivity, βi.
, and the sensitivity, βi.
 , is sometimes referred to as the systematic risk of asset i. The error variance term in Equation 11-13,
, is sometimes referred to as the systematic risk of asset i. The error variance term in Equation 11-13,  , is sometimes referred to as the nonsystematic risk of asset i.
, is sometimes referred to as the nonsystematic risk of asset i. , and on the sensitivities βi and βj.
, and on the sensitivities βi and βj.
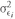 , as well as the expected return and variance for the market. Because we need to estimate only 3n + 2 parameters with the market model, we need far fewer parameters to construct the minimum-variance frontier than we would if we estimated the historical means, variances, and covariances of asset returns. For example, if we estimated the minimum-variance frontier for 1,000 assets (say, 1,000 different stocks), the market model would use 3,002 parameters for computing the minimum-variance frontier, whereas the historical estimates approach would require 501,500 parameters, as discussed earlier.
, as well as the expected return and variance for the market. Because we need to estimate only 3n + 2 parameters with the market model, we need far fewer parameters to construct the minimum-variance frontier than we would if we estimated the historical means, variances, and covariances of asset returns. For example, if we estimated the minimum-variance frontier for 1,000 assets (say, 1,000 different stocks), the market model would use 3,002 parameters for computing the minimum-variance frontier, whereas the historical estimates approach would require 501,500 parameters, as discussed earlier.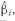 , of βi; we call this estimate an unadjusted beta. Later we will introduce an adjusted beta. We can use these estimates to compute the expected returns and the variances and covariances of those returns for mean—variance optimization.
, of βi; we call this estimate an unadjusted beta. Later we will introduce an adjusted beta. We can use these estimates to compute the expected returns and the variances and covariances of those returns for mean—variance optimization.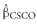 , is 2.09, and the residual standard deviation,
, is 2.09, and the residual standard deviation,  , is 11.52.
, is 11.52. , is 1.75, and the residual standard deviation,
, is 1.75, and the residual standard deviation,  , is 11.26.
, is 11.26.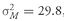 , which corresponds to an annual standard deviation of returns of about 18.9 percent. Using the data given, estimate the correlation of returns between Cisco and Microsoft.
, which corresponds to an annual standard deviation of returns of about 18.9 percent. Using the data given, estimate the correlation of returns between Cisco and Microsoft. and
and 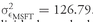 . Using the definition of correlation as covariance divided by the individual standard deviations, and using Equations 11-13 and 11-14, we have
. Using the definition of correlation as covariance divided by the individual standard deviations, and using Equations 11-13 and 11-14, we have
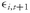 is an error term. If beta followed a random walk, the best predictor of βi,t +1 would be βi,t because the error term has a mean value of 0. The historical beta would be the best predictor of the future beta, and the historical beta need not be adjusted.
is an error term. If beta followed a random walk, the best predictor of βi,t +1 would be βi,t because the error term has a mean value of 0. The historical beta would be the best predictor of the future beta, and the historical beta need not be adjusted.
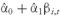 . In this case, the historical beta needs to be adjusted because the best prediction of beta in the next period is
. In this case, the historical beta needs to be adjusted because the best prediction of beta in the next period is  , not βi,t.
, not βi,t.

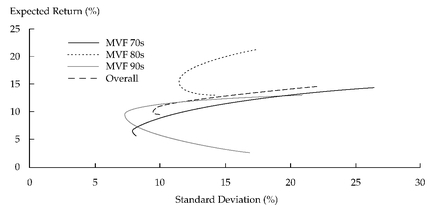



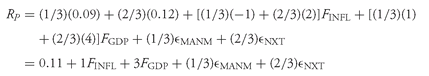
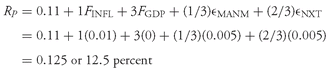
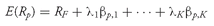
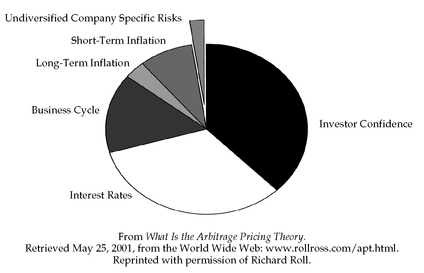






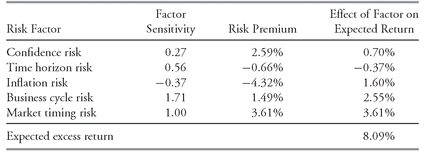
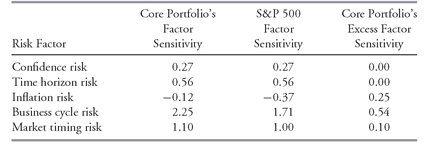
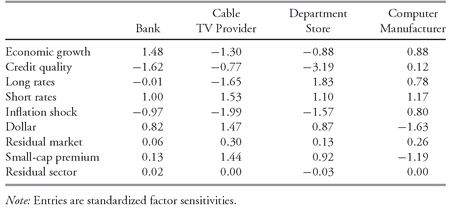





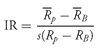
 and
and  stand for the sample mean return on the portfolio and the sample mean return on the benchmark, respectively. To illustrate the calculation, if a portfolio achieved a mean return of 9 percent during the same period that its benchmark earned a mean return of 7.5 percent, and the portfolio’s tracking risk was 6 percent, we would calculate an information ratio of (9%—7.5%)/6% = 0.25. Setting guidelines for acceptable active risk or tracking risk is one of the ways that some institutional investors attempt to assure that the overall risk and style characteristics of their investments are in line with those desired.
stand for the sample mean return on the portfolio and the sample mean return on the benchmark, respectively. To illustrate the calculation, if a portfolio achieved a mean return of 9 percent during the same period that its benchmark earned a mean return of 7.5 percent, and the portfolio’s tracking risk was 6 percent, we would calculate an information ratio of (9%—7.5%)/6% = 0.25. Setting guidelines for acceptable active risk or tracking risk is one of the ways that some institutional investors attempt to assure that the overall risk and style characteristics of their investments are in line with those desired.


 is the ith asset’s active weight in the portfolio (that is, the difference between the asset’s weight in the portfolio and its weight in the benchmark) and
is the ith asset’s active weight in the portfolio (that is, the difference between the asset’s weight in the portfolio and its weight in the benchmark) and  is the residual risk of the ith asset (the variance of the ith asset’s returns left unexplained by the factors).447 Active specific risk identifies the active nonfactor or residual risk assumed by the manager. We should look for a positive average return from asset selection as compensation for bearing active specific risk.
is the residual risk of the ith asset (the variance of the ith asset’s returns left unexplained by the factors).447 Active specific risk identifies the active nonfactor or residual risk assumed by the manager. We should look for a positive average return from asset selection as compensation for bearing active specific risk.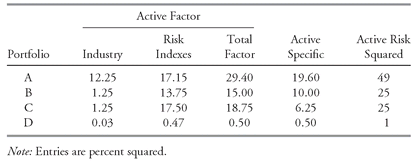

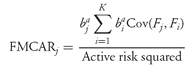
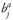 is the portfolio’s active exposure to factor j. The numerator is the active factor risk for factor j.449 The numerator is similar to expressions involving beta that we encountered earlier in discussing the market model, but with multiple factors, factor covariances as well as variances are relevant. To illustrate Equation 11-27 in a simple setting, suppose we have a two-factor model:
is the portfolio’s active exposure to factor j. The numerator is the active factor risk for factor j.449 The numerator is similar to expressions involving beta that we encountered earlier in discussing the market model, but with multiple factors, factor covariances as well as variances are relevant. To illustrate Equation 11-27 in a simple setting, suppose we have a two-factor model:  . The other active factor exposure is
. The other active factor exposure is 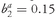 .
.