CHAPTER I
PROPERTIES OF THE TRIANGLE
A LIST of the fundamental formulae connecting the elements of a triangle, proofs of which have been given in Durell and Wright’s Elementary Trigonometry, will be found in Section D of the formulae at the beginning of that book ; references to these proofs will be indicated by the prefix E.T.
For geometrical proofs of theorems on the triangle, the reader is referred to some geometrical text-book. When these theorems are quoted or illustrated in this chapter, references, indicated by the prefix M.G., are given to Durell’s Modern Geometry.
Revision. Examples for the revision of ordinary methods of solving a triangle are given in Exercise I. a, below.
It is sometimes convenient to modify the process of solution. If, for example, the numerical values of b, c, A are given and if the value of a only is required, we may proceed as follows :
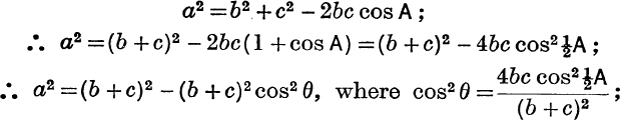
![]()
where
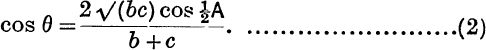
θ is first found from (2) and then a is obtained from (1), both equations being adapted to logarithmic work.
An angle θ, used in this way, is called a subsidiary angle. For other examples of the use of subsidiary angles, see Ex. I. a, Nos. 21 to 25.
EXERCISE I. a.
[Solution of Triangles]
1. What are the comparative merits of the formulae for cos A, cos![]() , sin
, sin![]() , tan
, tan![]() , when finding the angles of a triangle from given numerical values of a, b, c ?
, when finding the angles of a triangle from given numerical values of a, b, c ?
2. Given a = 100, b = 80, c = 50, find A.
3. Given a = 37, b = 61, c = 37, find B.
4. Given a = 11·42, b = 13·75, c = 18·43, find A, B, C.
5. Given A = 17° 55′, B = 32° 50′, c = 251, find a from the formula a = c sin A cosec C.
6. Given B = 86°, C = 17° 42′, b = 23, solve the triangle.
7. Given b = 16·9, c = 24·3, A = 154° 18′, find ![]() (B – C) from the formula
(B – C) from the formula ![]() , and complete the solution of the triangle.
, and complete the solution of the triangle.
8. Given b = 27, c = 36, A = 62° 35′, find a.
Solve the triangles in Nos. 9-13 :
9. A = 39° 42′, B = 81° 12′, c = 47·6.
10. b = 6·32, c = 8·47, B = 43°.
11. a = 110, b = 183, c = 152.
12. a = 6·81, c = 9·06, B = 119° 45′.
13. b = 16·9, c = 12·3, C = 51°.
[The Ambiguous Case]
14. Given A = 20° 36′, c = 14·5, find the range of values of a such that the number of possible triangles is 0, 1, 2. Complete the solution if a equals (i) 8·3, (ii) 16·2, (iii) 3·2, (iv) 5·1.
15. Given b, c, and. B, write down the quadratic for a, and the sum and product of its roots, a1 and a2. Verify the results geometrically.
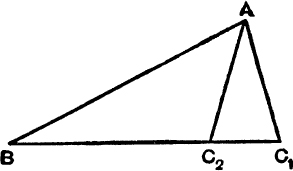
If A1, C1 and A2, C2 are the remaining angles of the two triangles which satisfy the data, find C1 + C2 and A1 + A2.
16. With the data of No. 15, prove that
![]()
17. With the data of No. 15, prove that
![]()
18. (i) With the data of No. 15, if a1 = 3a2, prove that
![]()
(ii) With the data of No. 15, if C2 = 2C1, prove that
![]()
19. If the two triangles derived from given values of c, b, B have areas in the ratio 3 : 2, prove that 25 (c2 – b2) = 24c2 cos2B.
20. With the data of No. 15, if A1 =2A2, prove that 4c3 sin2 B = b2(b +3c).
![]()
[Subsidiary Angles]
21. Given b = 16·9, c = 24·3, A = 154° 18′, find a from formulae (1) and (2), p. 1.
22. Show that the formula c = b cos A± ![]() (a2 – b2 sin2 A) may be written in the form c = a sin (θ ± A) cosec A, where
(a2 – b2 sin2 A) may be written in the form c = a sin (θ ± A) cosec A, where ![]() .
.
23. Show how to apply the method of the subsidiary angle to a2 = (b – c)2 + 2bc(l – cos A).
24. In any triangle, prove that tan ![]() (B – C) = tan (45° – θ)cot
(B – C) = tan (45° – θ)cot ![]() A, where
A, where ![]() .
.
Hence find ![]() (B – C) if b = 321, c = 436, A = 119° 15′.
(B – C) if b = 321, c = 436, A = 119° 15′.
25. Express a cos θ – b sin θ in a form suitable for logarithmic work.
[Miscellaneous Relations]
26. If a = 4, b = 5, c = 6, prove that C = 2A.
27. Express in a symmetrical form ![]() .
.
28. Prove that b2(cot A + cot B) = c2(cot A + cot C).
29. Simplify cosec (A – B) . (a cos B – b cos A).
30. Prove that a2 sin (B – C) = (b2 – c2) sin A.
31. Prove that ![]() .
.
32. If b cos B = c cos C, prove that either b = c or A = 90°.
33. Prove that sin2 A + sin B sin C cos A = ![]() .
.
34. Prove that 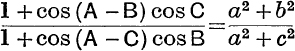 .
.
35. Prove that
![]()
36. Express cos ![]() (A – B). cosec
(A – B). cosec ![]() in terms of a, b, c,
in terms of a, b, c,
37. If b + c = 2a, prove that 4Δ = 3a2 tan ![]() .
.
38. If a2 = b(b + c), prove that A = 2B.
39. Prove that c2 = a2 cos 2B + b2 cos2A + 2ab cos(A – B).
40. Prove that ![]() .
.
41. Prove that
![]()
42. If cos A cos B + sin A sin B sin C = 1, prove that A = 45° = B.
The Circumcentre. The centre O of the circle through A, B, C is found by bisecting the sides of the triangle at right angles, and the radius is given by the formulae
![]()
![]()
The reader should prove that these formulae hold also when ![]() BAC is obtuse.
BAC is obtuse.
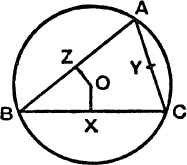
The in-centre and e-centres. The centres I, I1, I2, I3 of the circles which touch the sides are found by bisecting the angles of the triangle, internally and externally.
FIG. 2.
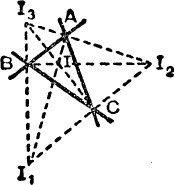
FIG. 3.
The radii of these circles are given by
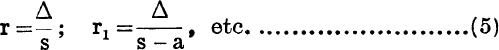
![]()
Also in Fig. 3, we have
![]()
For proofs of these formulae and further details, see E.T., pp. 184·186, 277, 278 and M.G., pp. 11, 24, 25.
The Orthocentre and Pedal Triangle. The perpendiculars AD, BE, CF from the vertices of a triangle to the opposite sides meet at a point H, called the orthocentre ; the triangle DEF is called the pedal triangle (M.G., p. 20).
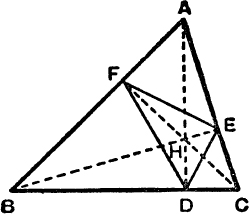
FIG. 4.
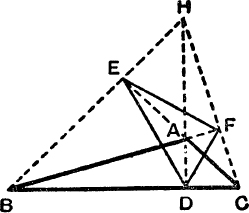
FIG. 5.
If Δ ABC is acute-angled, (Fig. 4), H lies inside the triangle.
Since BFEC is a cyclic quadrilateral, AFE and ACB are similar triangles ;

Since HECD is a cyclic quadrilateral, ![]() HDE =
HDE = ![]() HCE = 90° – A ; similarly
HCE = 90° – A ; similarly ![]() HDF = 90° – A ;
HDF = 90° – A ;
![]()
Further, HD bisects ![]() EDF and similarly HE bisects
EDF and similarly HE bisects ![]() DEF ; ∴ H is the in-centre of Δ DEF. Also since BC is perpendicular to AD, it is the external bisector of
DEF ; ∴ H is the in-centre of Δ DEF. Also since BC is perpendicular to AD, it is the external bisector of ![]() EDF ; hence A, B, C are the e-centres of the pedal triangle.
EDF ; hence A, B, C are the e-centres of the pedal triangle.
We have also
![]()
and
![]()
The reader should work out the corresponding results for Fig. 5, where the triangle is obtuse-angled.
If ![]() BAC is obtuse,
BAC is obtuse, ![]() EDF = 2A – 180° and other results are modified by writing – cos A for cos A. [See Ex. I. b, No. 27 and note the difference of form in No. 36. See also Example 3.]
EDF = 2A – 180° and other results are modified by writing – cos A for cos A. [See Ex. I. b, No. 27 and note the difference of form in No. 36. See also Example 3.]
The Nine-Point Circle. The circle which passes through the midpoints X, Y, Z of the sides BC, CA, AB passes also through D, E, F and through the mid-points of HA, HB, HC ; it is therefore called the nine-point circle and its centre N is the mid-point of OH (M.G., p. 27).
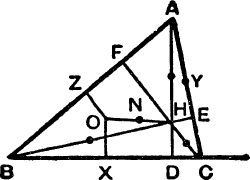
FIG. 6.
Since Δ XYZ is similar to Δ ABC and of half its linear dimensions, the radius of the nine-point circle is ![]() R.
R.
Since each of the points H, A, B, C is the orthocentre of the triangle formed by the other three, the circumcircle of Δ DEF is the common nine-point circle of the four triangles ABC, BCH, CHA, HAB.
Also, since Δ ABC is the pedal Δ of Δ I1I2I3 and of Δ II2I3, etc., the circumradius of each of these triangles is 2R.
The Polar Circle. In Fig. 6 and Fig. 7 we have, by cyclic quadrilaterals,
![]()
In Fig. 7, where ![]() BAC is obtuse, A and D are on the same side of H, and so also are B, E and C, F. In this case, if HA . HD = p2, it follows that the polars of A, B, C w.r.t. the circle, centre H, radius ρ, are BC, CA, AB.
BAC is obtuse, A and D are on the same side of H, and so also are B, E and C, F. In this case, if HA . HD = p2, it follows that the polars of A, B, C w.r.t. the circle, centre H, radius ρ, are BC, CA, AB.
The triangle ABC is therefore self polar w.r.t. this circle ; and the circle is called the polar circle of Δ ABC.
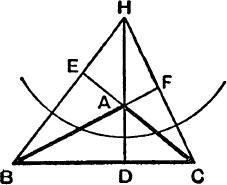
FIG. 7.
We have
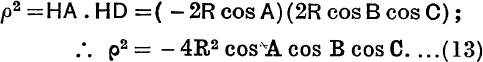
An acute-angled triangle in real geometry has no polar circle.
Notation. The lettering already adopted for special points connected with the triangle will be employed throughout the Chapter. This will shorten the statement of many of the examples.
We add some illustrative examples.
Example 1. Prove s2 = Δ(cot ![]() A + cot
A + cot ![]() B + cot
B + cot ![]() C).
C).
Since
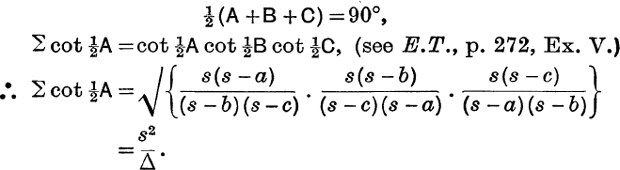
Example 2. Express 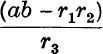 in a symmetrical form.
in a symmetrical form.
Since
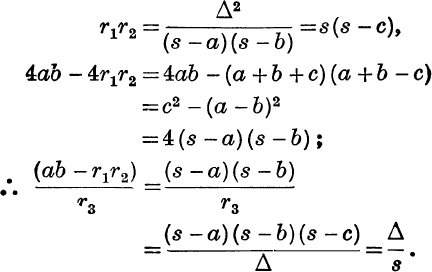
Example 3. If J is the in-centre of BHC, express the radius of the circle BJC in terms of R and A.
By equation (3) the radius is ![]() BC cosec BJC, but
BC cosec BJC, but
![]() BJC = 90° +
BJC = 90° + ![]()
![]() BHC = 180° –
BHC = 180° – ![]() A, if B and C are acute angles;
A, if B and C are acute angles;
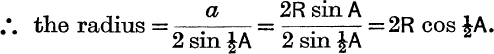
If either B or C is obtuse, ![]() BJC = 90° +
BJC = 90° + ![]() A, and then the radius = 2R sin
A, and then the radius = 2R sin ![]() A.
A.
EXERCISE I. b.
1. If a = 15·1, A =24° 36′, find R.
2. If a = 3, b = 5, c = 7, find R and r.
3. If a = 13, b = 14, c = 15, find r1, r2, r3.
4. If a = 23×5, A = 62°, and b = c, find R and r.
5. Prove that
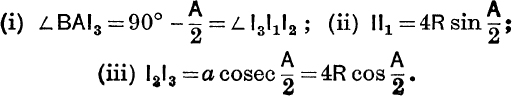
6. Verify Equation (6), p. 4, by using the formulae sin ![]() , cos
, cos ![]() , etc., in terms of the sides.
, etc., in terms of the sides.
7. Express a (cos A + cos B cos C) in a symmetrical form.
Prove the following relations :
8. ![]()
9. ![]()
10. r2r3 tan ![]() = Δ.
= Δ.
11. r2r3 + r3r1 + r1r2 = s2.
12. r2 + r3 = 4R cos2 ![]() .
.
13. r – r1 + r2 + r3 = 2a cot A.
14. AI . AI1 = bc.
15. IA. IB = 4Rr sin ![]() .
.
16. IA. IB. IC = ![]() .
.
17. II1. II2. II3 = 16R2r.
18. Δ ABI : Δ ACI = c : b.
19. AD2 (cot B + cot C) = 2Δ.
20. AD = 2r cosec ![]() cos
cos ![]() cos
cos ![]() .
.
21. Δ OI2I3 : Δ OI3I1 = (b + c) : (a + c).
22. AH = α cot A = 2OX.
23. AH + BH +CH = 2 (R + r).
24. If a = 14, b = 13, c = 15, prove that AD = 12.
25. Given B = 37°, C =46°, BE = 9×3, find 6.
26. If BP . PC = Δ, (see Fig. 3), prove that A =90°.
27. In Fig. 5, where ![]() BAC is obtuse, prove that
BAC is obtuse, prove that
(i) EF = –a cos A, FD = b cos B, DE = c cos C ;
(ii) ![]() FDE = 2A – 180°,
FDE = 2A – 180°, ![]() DEF = 2B,
DEF = 2B, ![]() EFD = 2C;
EFD = 2C;
(iii) AH = – 2R cos A, BH = 2R cos B, CH = 2R cos C;
(iv) HD = 2R cosB cos C, HE = – 2R cos C cos A,
HF = – 2R cos A cos B.
28. If a = 13, b = 9, c = 5, find ρ (see p. 6).
29. Find an expression for the radius of the polar circle of Δ II2 I3 in terms of R, r1.
30. Prove that the circumradius of Δ HBC equals R.
31. Prove that the circumradius of Δ OBC is > ![]() R.
R.
32. Prove that the in-radius of Δ AEF is r cos A.
33. Prove that the area of Δ DEF is ± 2A cos A cos B cos C.
34. Given b, c, B, prove that the product of the in-radii of the two possible triangles is c (c – b) sin2 ![]() B.
B.
35. Prove that the in-radius of Δ I1I2I3, is ![]() .
.
36. If Δ ABC is acute-angled, prove that the perimeter of Δ DEF is 4R sin A sin B sin C. If ![]() BAC is obtuse, prove that the perimeter is 4R sin Δ cos B cos C.
BAC is obtuse, prove that the perimeter is 4R sin Δ cos B cos C.
37. Find in terms of A, B, C, R the in-radius of Δ DEF (i) if Δ ABC is acute-angled, (ii) if ![]() BAC is obtuse.
BAC is obtuse.
38. Prove that a sin B sin C + b sin C sin A + c sin A sin B = ![]() .
.
39. Express ![]() + r Cos A – R cos2 A in a symmetrical form.
+ r Cos A – R cos2 A in a symmetrical form.
40. Prove that
(i) a2 cos2 A = b2 cos2 B + c2 cos2 C + 2bc cos B cos C cos 2A;
(ii) a2 cos2 A cos2 2A = b2 cos2B cos2 2B + c2 cos2 C cos2 2C + 2bc cos B cos C cos 2B cos 2C cos 4A;
(iii) a2 cosec2 ![]() = b2 cosec2
= b2 cosec2 ![]() + c2 cosec2
+ c2 cosec2 ![]() – 2bc cosec
– 2bc cosec ![]() cosec
cosec ![]() sin
sin ![]() .
.
Any Line through a Vertex. Suppose any line through A cuts BC at K. Denote ![]() by
by ![]() , so that K is the centroid of masses y, z at B, C respectively.
, so that K is the centroid of masses y, z at B, C respectively.
Let ![]() BAK = β,
BAK = β, ![]() KAC = γ,
KAC = γ, ![]() AKC = θ.
AKC = θ.
Draw BB′, CC′ perpendicular to AK.
Then
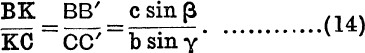
FIG. 8.
This may be written
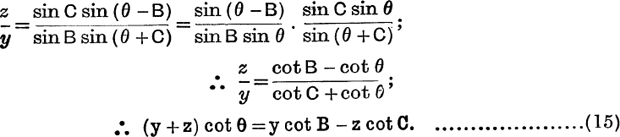
This relation, which determines θ for a given triangle and given position of K, is often useful in three-force problems in statics (cf. Ex. I. c, No. 11) ; an alternative method of proof is indicated in Ex. I. c, No. 8. Sometimes (cf. Ex. I. c, No. 12) it is convenient to have an expression for θ in terms of β, γ.
From (14),
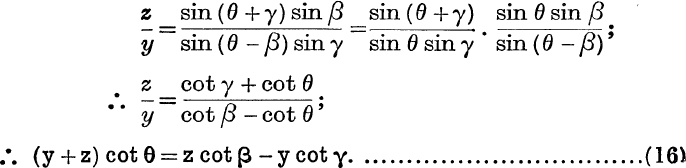
The Centroid. The centroid of k1 at (x1, y2), k2 at (x2, y2), k3 at (x3, y3), etc., is the centre of mass of particles of masses proportional to k1, k2, k3, etc., at these points. The centroid is also called the centre of mean position. The point may also be defined geometrically, and its coordinates are 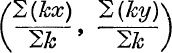 ; thus the idea of mass is not really involved. The values of the k’s need not all be positive, but ∑k must not be zero. (M.G., pp. 58-64.)
; thus the idea of mass is not really involved. The values of the k’s need not all be positive, but ∑k must not be zero. (M.G., pp. 58-64.)
If T is any point in AK, we have with the notation of Fig. 9,
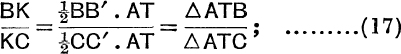
∴ K is the centroid of Δ CTA at B and Δ ATB at C;
FIG. 9.
∴ the centroid of Δ BTC at A, Δ CTA at B, Δ ATB at C lies on AK, that is on AT ; similarly it must lie on BT, and it is therefore at T.
Hence, if any point T is the centroid of masses λ, μ, v at A, B, C, then λ : μ: v = Δ TBC : Δ TCA : Δ TAB.
If, with the same notation as before, K is the centroid of y at B and z at C, the length of AK is given by a theorem of Apollonius (M.G., p. 61):
![]()
where
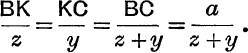
And more generally (M.G., p. 62) if G is the centroid of k1 at P1, k2 at P2, etc., and if O is any point,
![]()
Equation (19) is useful in dealing with expressions connected with Δ ABC of the form λ .TA2 + μ .TB2 + v .TC2. (Cf. Ex. I. c, Nos. 39, 40 and Ex. I. d, Nos. 22-28.)
Medians. If y = z, AK is a median ; we then have from (15) and (18)
![]()
![]()
The three medians of a triangle are concurrent at a point G, which is the centroid of equal masses at A, B, C or of equal masses at X, Y, Z
Further GX = ![]() AX and in addition G is the point on OH such that OG =
AX and in addition G is the point on OH such that OG = ![]() OH. (M.G., p. 28.)
OH. (M.G., p. 28.)
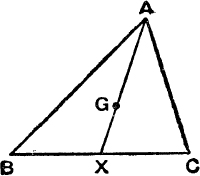
FIG. 10.
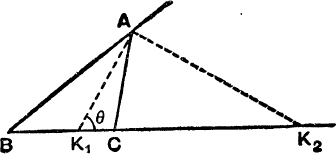
FIG. 11.
Angle-Bisectors. If AK1 is the internal bisector of ![]() BAC, β = γ =
BAC, β = γ = ![]() A and θ = B +
A and θ = B + ![]() A = 9O° –
A = 9O° – ![]() (C–B).
(C–B).
Also z: y = c : b; ∴ from (18), we have
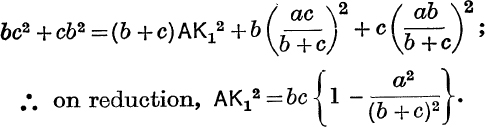
If AK2 is the external bisector of ![]() BAC,
BAC,
![]()
Also z : y = c : – b; ∴ from (18) as before, we have
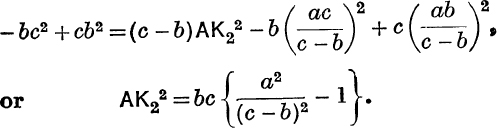
Direct methods of proof are indicated in Ex. I. c, Nos. 15, 16.
Example 4. Show that ∑ cot AXC = 0
![]()
Equation (20) gives
![]()
and equation (16), with y = z, gives
![]()
from which the required results follow.
Example 5. Find what masses at the vertices have their centroid at the circumcentre, and deduce that, if S is on the circle ABC,
![]()
The area BOC = ![]() R2 sin 2A;
R2 sin 2A;
∴ the ratios of the areas BOC, COA, AOB are
![]()
∴ the masses are proportional to sin2A, sin2B, sin2C (see p. 10). Hence, by equation (19),
EXERCISE I. c.
1. If AO meets BC at K, prove that ![]() .
.
2. If K is a point on the base BC of an equilateral triangle ABC and if ![]() BAK = 15°, calculate
BAK = 15°, calculate ![]() .
.
3. If B = C = 30° and if the perpendicular at A to AC cuts BC at K, prove that BK = ![]() KC.
KC.
4. If a = 13, b = 14, c = 15, find cot B, cot C and cot AXC.
5. If a = 61, b = 11, c = 60 and if K divides BC internally as 3 : 2, find cot AKC.
6. If a = 85, b = 13, c = 84 and if K divides BC externally as 3 : 2, find cot AKC.
7. Prove that tan AXC = ![]() .
.
8. If B, K, D, C are any four collinear points, prove that
![]()
From this relation, deduce equation (15) on p. 9.
9. Prove that abc cot AXB = R(b2 – c2).
10. If the trisectors of ![]() BAC meet BC in K, K′, prove that
BAC meet BC in K, K′, prove that
![]()
11. A uniform rod AB, 1 ft. long, is suspended from O by strings OA, OB of lengths 10 in., 7 in. ; find the angle between AB and the vertical.
12. A uniform rod AB rests with its ends on two smooth planes, as shown ; XOY is horizontal, find the angle between AB and the vertical.
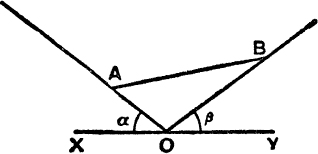
FIG. 12.
13. If a = 5, b = 4, c = 6 and if K divides BC internally as 3:2, find AK.
14. If ![]() XAC = 90°, prove that tan A + 2 tan C =0.
XAC = 90°, prove that tan A + 2 tan C =0.
15. If the internal bisector of ![]() BAC meets BC at K, prove that
BAC meets BC at K, prove that ![]() (b + c). AK sin
(b + c). AK sin ![]() = Δ, and deduce that
= Δ, and deduce that ![]() , and that
, and that
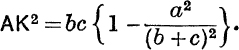
16. If the external bisector of ![]() BAC meets BC produced at K′, prove that
BAC meets BC produced at K′, prove that ![]() (c – b). AK′ cos
(c – b). AK′ cos ![]() = Δ, and deduce that
= Δ, and deduce that
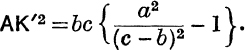
17. If the internal bisector of ![]() BAC meets BC at K, prove that
BAC meets BC at K, prove that
(i) AI : IK =(b + c) : a;
(ii) a . PD =(c – b) (s – a);
(iii) tan APC = ![]() .
.
18. If the internal bisector of ![]() BAC meets BC at K and the circumcircle at L, prove that AL =
BAC meets BC at K and the circumcircle at L, prove that AL = ![]() (b + c)sec
(b + c)sec ![]() . Find AK . AL and show that
. Find AK . AL and show that
![]()
19. Find the areas of Δ BOC, Δ BHC and deduce the area of Δ BNC. If AN meets BC at K, find ![]() .
.
20. Show that I is the centroid of a at A, b at B, c at C.
21. What is the centroid of – a at A, b at B, c at C ?
22. If H is the centroid of x at A, y at B, z at C, find x : y : z
23. Find the centroid of
(i) 1 at A, 1 at B, 1 at C, 1 at H ;
(ii) 3 at G, –2 at O.
24. Prove that AX2 + BY2 + CZ2 = ![]() (a2 + b2 + c2).
(a2 + b2 + c2).
25. If BY is perpendicular to CZ, prove that b2 + c2 = 5a2.
26. Prove that tan BGC = ![]() .
.
27. If BY cuts AD at T, prove that AT = ![]() .
.
28. If B = 55°, C = 23° 30′, AX =40, prove that BY![]() 60.
60.
29. If A = 90°, and if BC is trisected at Tl, T2, prove that
![]()
30. If A = B = 45° and if K is on AB, prove that AK2 + BK2 = 2CK2.
31. If AX = m, AD = h, prove that ![]() .
.
32. If ![]() BAX = β,
BAX = β, ![]() CAX = γ, prove that tan
CAX = γ, prove that tan ![]() tan
tan ![]() .
.
33. If the internal bisectors make angles θ, ϕ, Ψ with the opposite sides, prove that a sin 2θ + b sin 2ϕ + c sin 2Ψ = 0.
34. Prove that 3 cot BGC = cot A – ![]() .
.
35. If C = 2B and if CB is divided externally at Q in the ratio 4:1, prove that AQ – AC = ![]() QC.
QC.
36. If A, B, C, D are collinear and O is any point, prove that
![]()
37. If AU, BV, CW are concurrent lines cutting BC, CA, AB at U, V, W, prove that
![]()
38. If three segments AB, BC, CD of a straight line are of lengths α, β, γ and subtend equal angles θ at a point P, prove that
![]()
39. (i) Use equation (19) and No. 20 to show that
![]()
(ii) For what position of T is TA2 + TB2 + TC2 least ?
40. What is the locus of T, if
![]()
is constant ?
Distances between Special Points. With the usual notation,
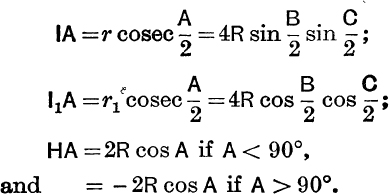
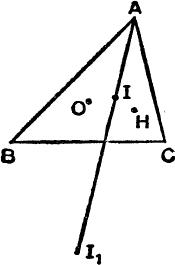
FIG. 13.
To find OI2 (M.G., p. 35).
Let C be one of the acute angles of the triangle ABC.
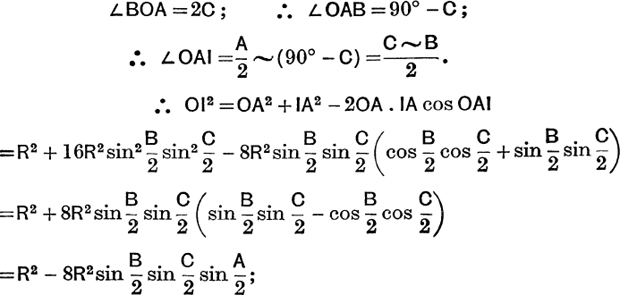
![]()
In the same way it can be proved that
![]()
To find OH2.
For an acute-angled triangle ABC, ![]() OAB = 90° – C,
OAB = 90° – C, ![]() HAB = 90° –B,
HAB = 90° –B,
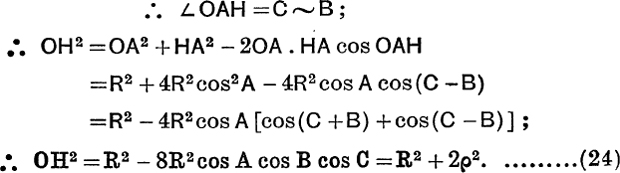
If A > 9°, ![]() HAB = 90° + B; ∴ cos OAH = –cos (C – B); also
HAB = 90° + B; ∴ cos OAH = –cos (C – B); also
![]()
∴ the final result is the same as before.
For an acute-angled triangle ABC, ![]() I1AH =
I1AH = ![]() ~ (90° – C) =
~ (90° – C) = ![]() ;
;
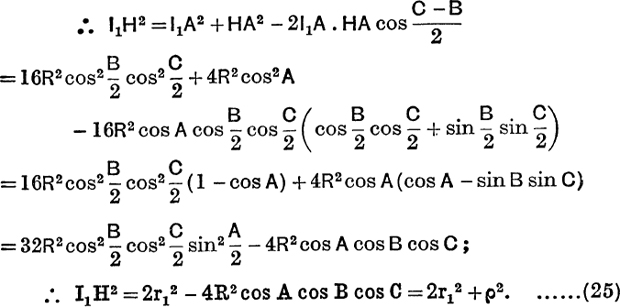
In the same way it can be proved that
![]()
The reader should verify that these results are also true for an obtuse-angled triangle.
A geometrical method of proof of (24) is indicated in Ex. I. d, No. 21.
The reciprocity of the relations (24) and (26) is explained by the following argument: since Δ ABC circumscribes its own in-circle and is self-polar w.r.t. its own polar circle, there exists a triangle αβγ which is inscribed in this polar circle, and is self-polar w.r.t. this in-circle (Durell’s Projective Geometry, p. 209). ∴ H is the circumcentre, ρ is the circumradius, I is the orthocentre, r is the polar-radius of Δ αβγ.
∴applying (24) to Δ αβγ, we have HI2 = ρ2 +2r2.
To find IN.
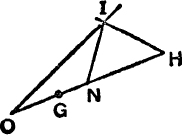
FIG. 14.
The nine-point centre N is the mid-point of OH ;
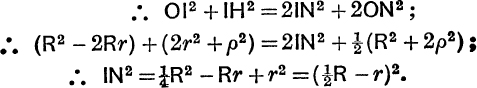
But OI2 = R(R – 2r); ∴ R ≥ 2r;
![]()
In the same way it can be proved that.
![]()
Since the radius of the nine-point circle is ![]() R, equations (27) and (28) prove that the nine-point circle touches the in-circle and the escribed circles [Feuerbach’s Theorem, M.G., p. 117].
R, equations (27) and (28) prove that the nine-point circle touches the in-circle and the escribed circles [Feuerbach’s Theorem, M.G., p. 117].
Example 6. If IH is parallel to BC, find a relation between the cosines of the angles of the triangle.
I and H will be equidistant from BC, thus r = 2R cos B cos C, thus
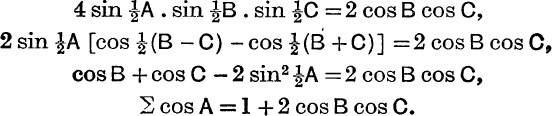
Example 7. Express IG in terms of the radii of the various circles connected with the triangle.
By equation (19) we have, since G is the centroid of 2 at O and 1 at H, (see Fig. 14)
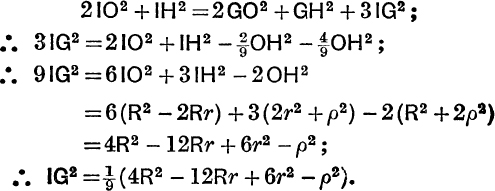
EXERCISE I. d.
1. If OI is parallel to BC, prove that cos B + cos C = 1.
2. If IG is parallel to BC, prove that r1 = 3r.
3. Prove OI2 = R2 [3 – 2∑(cos A)].
4. Prove II12 = 4R (r1 – r) and I2I32 = 4R (r2 + r3).
5. Prove II22 + I1I32 = II32 + I1I22.
6. Prove OH2 = 9R2 – a2 – b2 – c2.
7. If A = 60°, prove OH2 = (3R + 2r) (R – 2r).
8. Prove tan IAX = tan2![]() tan
tan![]() .
.
9. If in a scalene triangle IG is perpendicular to BC, prove that
![]()
10. If O lies on the in-circle, prove that cos A + cosB + cos C = ![]() 2.
2.
11. If OH makes an angle ϕ with BC, prove that
![]()
12. Prove that
![]()
13. Prove that ρ2 = (r + 2R)2 – s2.
14. If the circumcircle cuts the nine-point circle orthogonally prove that cos A cos B cos C = – ![]() .
.
15. If AH = r, prove that the circumcircle cuts one escribed circle orthogonally.
16. If OI cuts AD at T, prove OT = OI cos![]() cosec
cosec ![]() .
.
17. Prove that the area of Δ OIH is
![]()
18. If S is the circumcentre of Δ BHC, prove that
![]()
19. If IO = IH, prove that either AO = AH or A, O, I, H are concyclic. Deduce that an angle of the triangle is 60°.
20. Prove NI + NI1 + NI2 + NI3 = 6R.
21. If ![]() BAC is obtuse and if HA cuts the circumcircle at T, prove that (i) HT = 2HD ; (ii) HA . HT = 2ρ2. Hence show that
BAC is obtuse and if HA cuts the circumcircle at T, prove that (i) HT = 2HD ; (ii) HA . HT = 2ρ2. Hence show that
![]()
22. Prove that
(i) OI2 + OI12 + OI22 + OI32 = 12R2 ;
(ii) NA2 + NB2 + NC2 + NH2 = 3R2.
23. Prove that
(i) DA2 + DB2 + DC2 + DH2 = 4R2 ;
(ii) AI12 + AI22 + AI32 + AI2 = 16R2.
24. Prove that HA2 + HB2 + HC2 – HO2 = 3R2.
25. Prove that AG2 + BG2 + CG2 = ![]() R2 (1 + cos A cos B cos C).
R2 (1 + cos A cos B cos C).
26. Prove that a . IA2 + b . IB2 + c . IC2 = 4Rrs; find a similar expression for a . I3A2 + b. I3B2 – c . I3C2.
27. If T is any point, prove that
TA2 . sin 2A +TB2 . sin 2B +TC2. sin 2C = 4 (R2 + OT2) sin A sin B sin C.
28. If T is a point on the in-circle, prove that
![]()
29. Prove that the common chord of the circumcircle and the escribed circle, centre I1, is ![]() .
.
30. If t1, t2, t3 are the lengths of the tangents from I1, I2, I3 to the circumcircle, prove that (i) 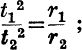 (ii)
(ii) ![]() .
.
Solution of Triangles from Miscellaneous Data. No general rules can be given, but the following typical examples may be useful.
(i) Given a, b – c, A.
In Fig. 15, cut off AK = AB ; then KC = b – c.
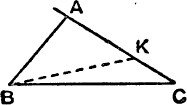
FIG. 15.
Also ![]() BKC = 90° +
BKC = 90° + ![]() A and
A and ![]() KBC =
KBC = ![]() (B – C);
(B – C);
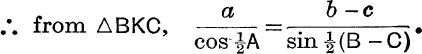
This determines ![]() (B – C) and therefore B, C.
(B – C) and therefore B, C.
(ii) Given a, R, Δ.
A is given by the relation ![]() .
.
Also, cos (B – C) + cos A = 2 sin B sin C = 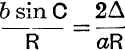 .
.
This determines (B – C) and therefore B and C since A has been found.
(iii) Given the altitudes p1, p2, p3.
The ratios a: b: c are given by 2Δ = ap1 = bp2 = cp3.
A is then given by 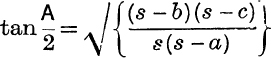 ; also c = p2 cosec A.
; also c = p2 cosec A.
(iv) Given r1; r2, r3.
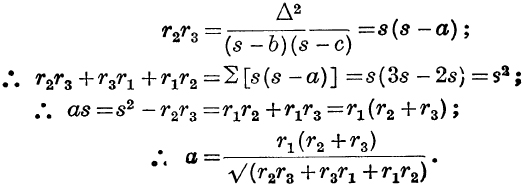
EXERCISE I. e.
1. Given a – b = 19·8, c = 22·2, C = 29° 16′, find B.
2. Given b = 3·36, a + c = 9·28, B = 37° 25′, find A.
3. Given AD = 6, BE = 8, CF = 9, find A and a.
4. Given b = 8, c = 10, AX = 7, find A.
5. Given A = 45°, a = 2 (b – c), find B.
6. Given r = 5, r1 = 12, r2 = 20, find a, c.
7. Given b, B and that a + c = 2b, show how to solve the triangle.
8. Express bc and b2 + c2 in terms of a, R, Δ.
9. Express sin ![]() A in terms of r1, r2, r3.
A in terms of r1, r2, r3.
10. Express tan B in terms of b, c, A.
11. Express c in terms of a, b, A.
12. Given B, b, c2 – a2, show how to find C.
13. Given A = 53° and BE = 2CF, find B.
14. Given A = 42°, r = 3·5, find the least possible value of a.
15. Given a = ![]() 57, A = 60°, Δ = 2
57, A = 60°, Δ = 2![]() 3 find b, B.
3 find b, B.
16. Given A = 60°, b – c = 4, AD = 11, find a and sin ![]() .
.
17. Given cot(B – C) = 7 and BC = 5AD, find cot B.
18. Given a, s, A, show how to find B.
19. Express a in terms of r, A, p where p = AD.
Errors. If u is a known function, f(x), of x, we have, using differentials : du = f′ (x). dx. If the value of u is calculated from a measured or observed value of x, the resulting error δu in u, due to an error δx in x is given by
![]()
If u is a known function of several independent variables x, y, z, etc., then the error in u due to errors in the values of x, y, z, etc., is given by
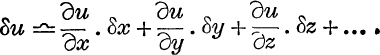
Example 8. The area of Δ ABC is calculated from measurements of B, C, a; find the error in the calculated value of Δ due to an error δB in the measured value of B.
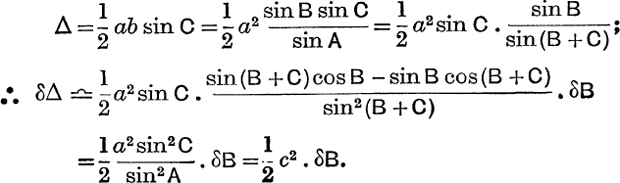
Here, δB is measured in radians; thus an error of 1′ in B causes an error of approximately ![]() in Δ.
in Δ.
If there are errors δB, δC, δa in B, C, a, the resulting error in Δ is given by
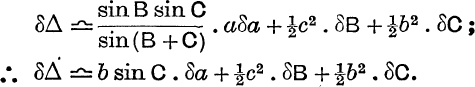
EXERCISE I. f.
1. If Δ is expressed as a function of a, B, C, prove that ![]() .
.
2. If Δ is expressed as a function of a, b, c, prove that
![]()
3. If A is calculated from measurements of a, b, c, prove that the error due to a small error y in b is about ![]() radians.
radians.
4. If R is calculated from measurements of a, b, c, prove that the error due to a small error x in a is about ![]() x cosec A cot B cot C.
x cosec A cot B cot C.
5. The base AB of a triangle ABC is fixed and the vertex C moves along the arc of a circle of which AB is a chord, prove that
![]()
6. An observer, on the ground, 50 ft. from a vertical tower, observes the angles of elevation of two marks on the tower to be 45° and 30°. Find the approximate error to which the calculated distance between them is liable if there may be an error of 1′ in each observed angle.
7. If c is calculated from measurements of a, b, C, prove that the error due to small errors x, y, γ in a, b, C is about
![]()
8. With the data of No. 7, prove that the relative error ![]() in the calculated area of the triangle is approximately
in the calculated area of the triangle is approximately ![]() .
.
9. If C is calculated from measurements of a, b, c in which there are small errors x, y, z, prove that the error in C is approximately ![]() cosec B –
cosec B – ![]() cot B –
cot B – ![]() cot A.
cot A.
10. If c is calculated from measurements of a, b, R and if there is a small error x in a, prove that the error in c is approximately
![]()
11. The area Δ of a triangle on a given base c is expressed in terms of c, A, B. Prove that
![]()
In finding the vertex when the base is accurately known and the base angles are subject to small errors ±α, ±β, show that the area of the small region within which the vertex must lie is approximately
![]()
12. The area ABC was calculated from the measured values a, b, 90° of BC, CA, ACB and it was found that the calculated area was too great by z and that a – x, b – y were the true lengths of BC, CA. Show that the error in C was about 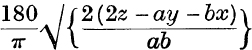 degrees, if z, x, y were small.
degrees, if z, x, y were small.
MISCELLANEOUS EXAMPLES
EXERCISE I. g.
1. If a + b = 2c, prove that cot![]() + cot
+ cot ![]() = 2 cot
= 2 cot ![]() .
.
2. Prove that ∑(ab sin2 C) = 2s . ∑(a cos B cos C).
3. Prove that 2aR sin (B – C) = b2 – c2.
4. Prove that Δ = r2 cot ![]() cot
cot ![]() cot
cot ![]() .
.
5. Prove that (r1 – r) cot2 = r2 + r3.
6. Prove that a2 = (r1 – r) (4R – r1 + r).
7. Prove that IA . II1 = 4Rr.
8. Prove that ![]() .
.
9. Prove that the circumradius of Δ IBC is 2R sin![]() and find that of Δ I1BC.
and find that of Δ I1BC.
10. Prove that 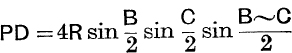 .
.
11. Prove that ![]() .
.
12. Prove that AD cuts the in-circle at an angle
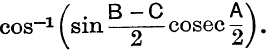
13. Given ![]() , prove that the triangle is right-angled.
, prove that the triangle is right-angled.
14. If B = 18°, C = 36°, prove that a – b = R.
15. If cos A + cos B = ![]() , prove that 2r – R = 2R cos C.
, prove that 2r – R = 2R cos C.
16. Given a, b, B, find the difference between the in-radii of the two triangles.
17. Prove that ∑(a3cos A) = abc (1 + 4 cos A cos B cos C).
18. Prove that rl, r2, r3 are the roots of
![]()
19. Prove that 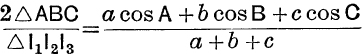 .
.
20. If T is the mid-point of EF, prove that XT = ![]() asin A.
asin A.
21. If a2 cos2 A + b2 cos2 B = c2 cos2 C, prove that one of the angles A, B, C is determinate, and find it.
22. If ![]() CAX = 90°, prove that 3accos A cos C = 2(c2 – a2).
CAX = 90°, prove that 3accos A cos C = 2(c2 – a2).
23. If a, b, c are in A.P., prove that
![]()
24. ABC, ABD are equilateral triangles in perpendicular planes ; calculate ![]() CAD.
CAD.
25. If B = C = 2A, prove that ![]() .
.
26. If DT, DT′ are perpendicular to AB, AC, prove that ![]() .
.
27. Prove that the tangents at A, B, C to the circumcircle form a triangle of area ±R2 tan A tan B tan C.
28. Prove that the radii of the circles which touch AB, AC and the circumcircle are r sec2![]() and r1 sec2
and r1 sec2![]() . [Use Inversion.]
. [Use Inversion.]
29. If l, m are the directed lengths of the perpendiculars from A, B to any line through C, prove that
![]()
[If A and B are on opposite sides of the line, l and m must be regarded as opposite in sign.
30. Prove that, if a > b > c, the length of the shortest line which bisects the area of ABC Is ![]() (2Δ tan
(2Δ tan ![]() C).
C).
31. If the angles of a triangle are calculated from measured values of the sides > show that the small errors satisfy
![]()
32. If r is calculated from measured values of a, b, c, show that the error due to an error x in a is
![]()