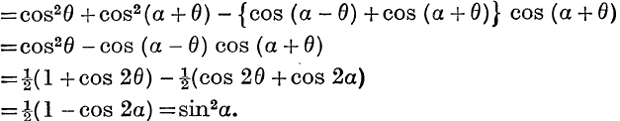
CHAPTER XIV
Numerical, Single-letter, and Two-letter Identities.
Example 1. Prove that cos2θ + cos2(α + θ) – 2 cos α cos θ cos (α + θ) is independent of θ.
First Method. The expression
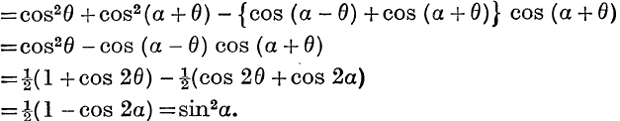
Second Method.
If
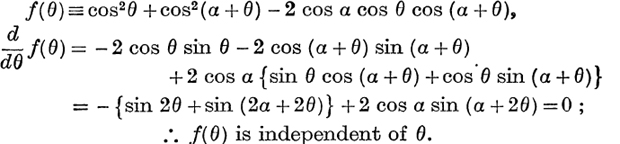
Third Method. Take a circle with diameter OD of unit length, and draw chords OB, OA making angles θ, α + θ with that diameter, as in Fig. 79; then OB = cosθ, OA = cos(α + θ), and AB = sin α. The expression
![]()
which is independent of θ.
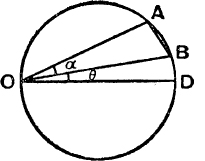
FIG. 79.
Fourth Method. Take a triangle ABC having ![]() , and hence C = α; then c2 = a2 + b2 – 2ab cos C;
, and hence C = α; then c2 = a2 + b2 – 2ab cos C;
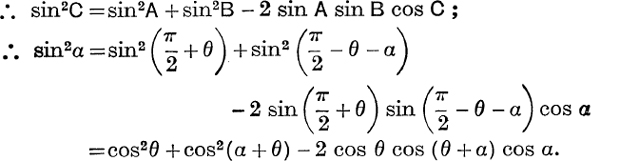
It should be noticed that the geometrical methods have to be modified, or interpreted in accordance with certain conventions for some values of α and θ.
EXERCISE XIV. a.
1. (cos A + sin A) (cot A + tan A) = cosec A + sec A.
2. (2 -cos2B)(2 +tan2B) _=(1 +2 tan2B)(2 -sin2B).
3. tan2C +cot2C = cosec2C sec2C – 2.
4. If sec D + cosec D = ![]() , then cos3D + sin3D = –
, then cos3D + sin3D = – ![]() .
.
5. cos2 22![]() ° – cos2 67
° – cos2 67![]() ° = cos 45°.
° = cos 45°.
6. 2 cos 5° 37′ 30″ = ![]() .
.
7. 4 cos 24° cos 36° cos 84° = sin 18°.
8. tan 9° – tan 27° – tan 63° + tan 81° = 4.
9. cos 12° + cos 60° + cos 84° = cos 24° + cos 48°.
10. sin 40° sin 50° = sin 30° sin 80°.
11. tan 20° tan 40° = tan 10° tan 60°.
12. If x : y : z : 1 = sin 40° : sin 60° : sin 80° : sin 20°, then
![]()
13. cos2 14° – cos 7° cos 21° = sin2 7°.
14. If tan ![]() = t, then tan θ + sec θ =
= t, then tan θ + sec θ = ![]() .
.
15. If cot A – tan A = x, then ![]() .
.
16. If sec 2A = 2 + sec A, then cos 2A +cos 3A = 0.
17. cosec 2θ + cot 4θ = cot θ – cosec 4θ.
18. 4(cos 2θ + cos 6θ)(cos 6θ + cos 8θ) = 1 + sin 150 cosecθ.
19. cot3θ + tan3θ = 8 cosec32θ – 6 cosec 2θ.
20. sin3θ sin 3θ + cos3θ cos 3θ = cos32θ.
21. sin3(60° + 0) + sin3(60° – θ) = ![]() .
.
22. 3 tan θ – 2 cot θ = cosec 2θ – 5 cot 2θ.
23. If α + β = ![]() , then
, then 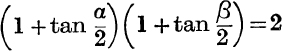 .
.
24. If tan2A = 1 + 2 tan2B, then cos 2B = 1 + 2 cos 2A.
25. If tan 2θ = μ cosec 2α – cot 2α, then 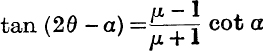 .
.
26. If ![]() , then
, then
![]()
27. If (1 + e cos α)(l – e cos β) = 1 – e2, and e is not zero, then
![]()
28. If ![]() , then
, then
![]()
29. ![]() .
.
30. 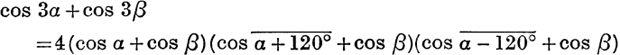 .
.
31. If 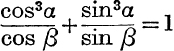 , then sin 2α + 2 sin (α + β) = 0.
, then sin 2α + 2 sin (α + β) = 0.
32. If (2 cos α – cos 2α) sin 3β – (2 sin α – sin 2α) cos 3β = 3 sin β and α ≡ 2(β + nπ), then ![]() .
.
Conditional Identities.
Example 2. If A + B + C = π, prove that
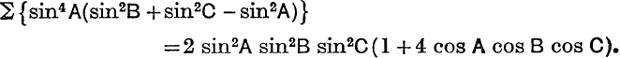
We have ∑x(y + z)2 ≡ (y + z)(z + x)(x + y) + 4xyz.
Putting b2 + c2 – a2, c2 + a2 – b2, a2 + b2 – c2 for x, y; z, the identity gives
![]()
where A, B, C are the angles of the triangle with sides a, b, c. Since a : b : c = sin A : sin B : sin C, it follows that
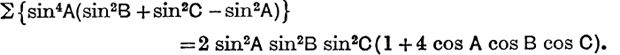
Example 3. If x + y + z = 0, prove that
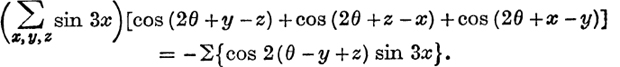
The left-hand side may be written
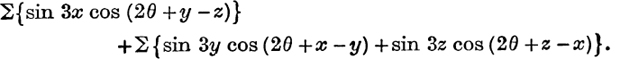
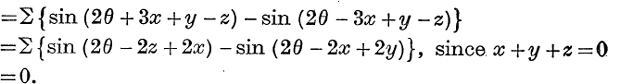
The second term
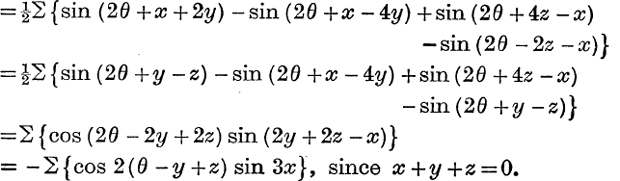
EXERCISE XIV. b.
In this Exercise, it is to be assumed that A + B + C = π,. or that A + B + C + D = 2π.
Prove the following :
1. cos2A + cos2B + cos2C + 2 cos A cos B cos C = 1.
2. sin2B +sin2C – 2 sin B sin C cos ![]() is symmetrical.
is symmetrical.
3. 1 + cos 2A + cos 2B + cos 2C = – 4 cos A cos B cos C.
4. sin 3A +sin 3B +sin 3C = – 4 ![]() .
.
5. ![]() .
.
6. ![]() .
.
7. sin 2A sin2A + sin 2B sin2B + sin 2C sin2C = sin 2A sin 2B sin 2C + 2 sin A sin B sin C.
8. sin4A + sin4B + sin4C = 2 (sin2B sin2C + sin2C sin2A + sin2A sin2B) – 4 sin2A sin2B sin2C.
9. sm 5A +sm 5B +sm 5C = ![]() .
.
10. 4(cos5A + cos5B + cos5C) = ![]() .
.
11. sin 2nA + sin 2nB +sin 2nC = – 4 cos nπ sin nA sin nB sin nC.
12. cot A + cot B + cot C = cot A cot B cot C + cosec A cosec B cosec C.
13. (tan A + tan B + tan C)(cot A + cot B + cot C) – sec A sec B sec C is constant.
14. If
cos A = cot β cot γ, cos B = cot γ cot α, and cos C = cot α cot β, then cos2α + cos2 β + cos2γ = 1.
15. If 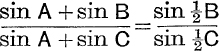 , then B = C.
, then B = C.
Deduce that, if two angle-bisectors of a triangle are equal, then the triangle is isosceles.
16. If (m + n) tan A + (n + l) tan B + (l + m) tan C = 0, then
![]()
17. ![]() .
.
18. sin A + sin B + sin C + sin D = ![]() .
.
19. 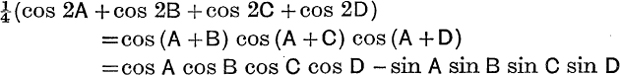 .
.
20. 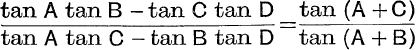 .
.
21. If 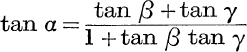 , then
, then 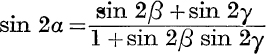 .
.
22. If ![]() , then
, then 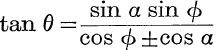 .
.
23. sin α sin(β – γ) + sin β sin (γ – α) + sin γ sin (α – β) = 0, and deduce that
![]()
24. ∑ sin β sin γ sin (β – γ) = – sin(β – γ) sin(γ – α) sin (α – β).
25. 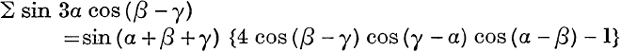 .
.
26. 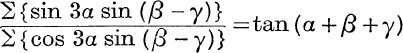 .
.
27. 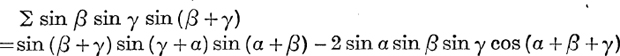 .
.
28. ∑ {sin 2α sin(γ – β)} = ∑ sin (β – γ) . ∑ sin(β + γ).
29. If cos 2α + 2 sin β sin γ = 0 = cos 2β + 2 sin γ sin α, prove that, in general, cos 2γ + 2 sin α sin β = 0.
30. If 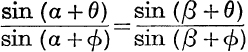 , prove that α – β or θ – ϕ is nπ.
, prove that α – β or θ – ϕ is nπ.
31. If sin3θ + sin (A + θ) sin (B + θ) sin (C + θ) = 0, prove that
![]()
32. sin s sin (s – α) sin (s – b) sin (s – c) + cos s cos (s – α) cos (s – b) cos (s – c) = cos a cos b cos c, where a + b + c = 2s.
Miscellaneous Transformations.
Example 4. If tan α = tan3β and tan 2β = 2 tan γ, prove that
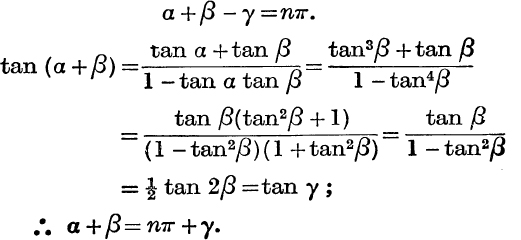
EXERCISE XIV. c.
1. If ![]() , prove that
, prove that
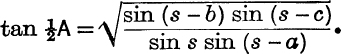
where 2s = a + b + c.
2. If tan(B + C – A) + tan(C + A – B) + tan(A + B – C) = tan(A + B + C), prove that A or B or C is ![]() .
.
3. If sin x + sin y + sin z = ![]() , prove that x + y + z = nπ.
, prove that x + y + z = nπ.
4. If cos 2A + cos 2B + cos 2C + cos (2A + 2B +2C) = 0, prove that
![]()
5. If cos 2A + cos 2B + cos 2C + 1 + 4 cos A cos B cos C =0, prove
![]()
6. If (sin α + sin β + sin γ)2 + (cos α + cos β + cos γ)2 = 1, prove that two of tho angles differ by (2n + 1)π.
7. If 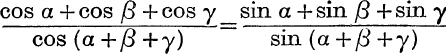 , prove that ∑ sin (β + γ) = 0, and that each fraction = ∑ cos (β + γ).
, prove that ∑ sin (β + γ) = 0, and that each fraction = ∑ cos (β + γ).
8. If ![]() and θ – ϕ ≠ 2nπ, prove that ∑ sin θ = – sin (∑θ), and that
and θ – ϕ ≠ 2nπ, prove that ∑ sin θ = – sin (∑θ), and that ![]() .
.
9. If 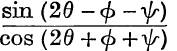 and
and 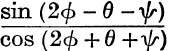 are equal, and if θ – ϕ ≠ nπ, prove that
are equal, and if θ – ϕ ≠ nπ, prove that 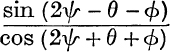 is equal to them.
is equal to them.
10. If sin 2x = k tan β and sin 2y = k tan α, and x – y = α – β = 0, α + β ≠ nπ, prove that sin 2x + sin 2y = – 2 sin (α + β) cos (x + y), and that sin (α + β – x – y) = k tan (x + y).
11. If 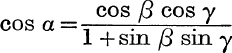 , prove that
, prove that ![]() .
.
12. If ∑ cos α = 0 = ∑ sin α for three angles α, β, γ between + π and – π, prove that these are of the form ![]() , and deduce that
, and deduce that
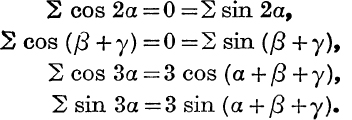
13. Show how to use de Moivre’s Theorem to prove the last two results in No. 12.
14. If ∑ cos α = 0 = ∑ sin α, prove
![]()
15. If ![]() , prove that either A + B + C = nπ or tan A + tan B = 2 tan C.
, prove that either A + B + C = nπ or tan A + tan B = 2 tan C.
16. If sin2x + sin2y + sin2z = 1 + 2 sin x sin y sin z, prove that
![]()
17. If a triangle inscribed in an ellipse has its centroid at the centre of the ellipse, show that the eccentric angles of its vertices satisfy ∑ cos α = 0 = ∑ sin α, and conversely.
18. If a triangle inscribed in an ellipse has its centroid at the centre, prove that the tangents at the vertices are parallel to the opposite sides. [Use No. 12 or geometry.]
Some easy examples have been given in E.T., p. 266. The following illustrate other methods.
Example 5. Eliminate θ from the equations
![]()
We have
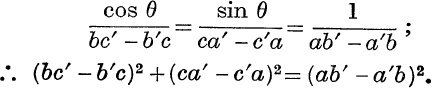
Example 6. Eliminate θ from the equations
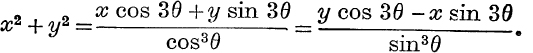
Each expression
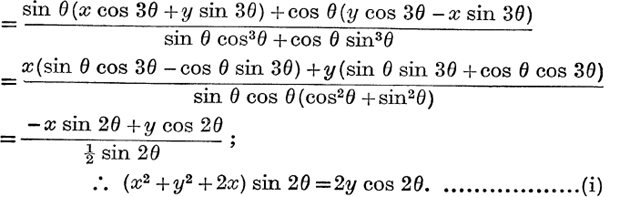
Also each expression
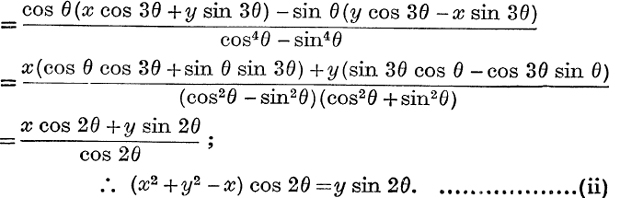
From (i) and (ii),
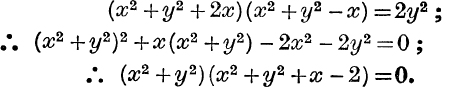
EXERCISE XIV. d
Eliminate θ from :
1. tan α = cos θ tan β, tan θ sin α = tan γ.
2. α sin α = b, α sin (θ – α) = c.
3. α cos2θ + b sin2θ = c, (b – c) tan2θ + (c – α) cot2θ = d.
4. a sin θ = b sin 2θ, c cos θ = d cos 2θ.
5. sin θ + sin 2θ = a, cos θ + cos 2θ = b.
6. sin3θ = a, cos3θ = b; also express the result in a rational form.
7. 3 sin θ + 2 cos θ = a, 2 sin θ + 3 cos θ = b.
8. 3 cos θ + cot θ = a, 4 cos θ – cot θ = b.
9. x + cos θ = sec θ, y + sin θ = cosec θ.
10. a sin θ(4 cos2θ – 1) = x, b cos θ(4 sin2θ – 1) = y.
11. 1 + sin2θ = a sin θ, 1 + cos2θ = b cos θ.
12. x cos θ + y sin θ = α sin 2θ, – x sin θ + y cos θ = 2α cos 2α.
13. x cos θ + y sin θ = α cosec θ, x sin θ – y cos θ = α cosec θ cot θ.
14. x cos θ + y sin θ = c = x cos (θ + α) + y sin (θ + α).
15. a + b cos θ + c cos 2θ = 0, 2α cos θ + b cos 2θ + c cos 3θ = 0.
16. ax sec θ – by cosec θ = c2, ax sec θ tan θ + by cosec θ cot θ = 0.
17. ![]() , x sin θ – y cos θ =
, x sin θ – y cos θ = ![]() .
.
18. a sin θ + b cos θ = c, a cosec θ + b sec θ = d.
19. tan θ + tan 2θ = c, cot θ + cot 2θ = d.
20. 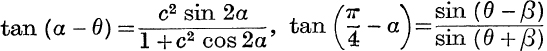 .
.
21. (a + b) tan (θ – a) =(a – b) tan (θ + α), a cos 2α + b cos 2θ = c.
22. ![]() .
.
23. x : a : b = cos θ + e cos α : sin θ : 1 + e cos (θ + α), where b2 = a2(l – e2).
24. x = tan–1 (θ + α) + tan–1 (θ – α), y = sin–1θ.
Elimination. Two Variables.
Example 7. Eliminate θ and ϕ from the equations,
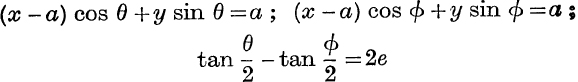
given that θ and ϕ are unequal and between 0 and 2π.
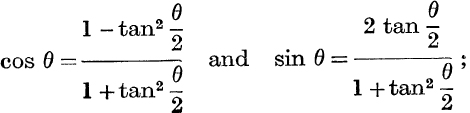
![]()
![]() and
and ![]() (being unequal) are the two roots of
(being unequal) are the two roots of
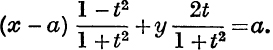
This reduces to xt2 – 2yt + 2a – x = 0;
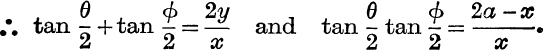
But
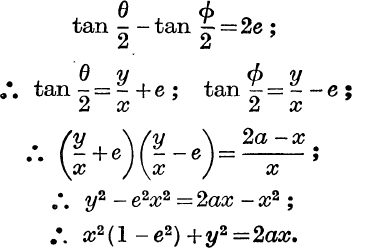
EXERCISE XIV. e.
Eliminate θ and ϕ in Nos. 1 to 12 :
1. sin θ – sin ϕ = 2a, cos θ – cos ϕ = 2b, θ – ϕ = 2γ.
2. x = a sin (θ – ϕ), y = 2a cos ϕ cos ϕ, θ + ϕ = a.
3. sin θ + sin ϕ = a, cos θ + cos ϕ = b, tan θ – tan ϕ = c sec θ sec ϕ.
4. sin θ + sin ϕ = x, cos θ + cos ϕ = y, ![]()
![]() = z.
= z.
5. sin θ + sin ϕ = s, tan θ + tan ϕ = t, sec θ + sec ϕ = k
6. cos θ +cos ϕ = a, cos 2θ + cos 2ϕ = b, cos 3θ + cos 3ϕ = c.
7. y tan θ = x tan2θ + a, y tan ϕ = x tan2ϕ + a, tan θ tan ϕ = – 1.
8. 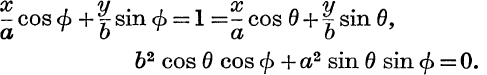
9. cos θ = cos α cos β, cos γ = cos β cos γ, ![]() .
.
10. x cos θ + y sin θ = x cos ϕ + y sin ϕ = 2a, ![]() .
.
11. 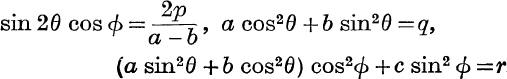 .
.
12. 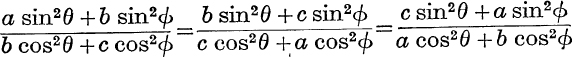 .
.
13. Eliminate A and B from a sin B = b sin A, c = a cos B + b cos A, and d = cos(A + B).
14. Eliminate θ, ϕ, and ψ from
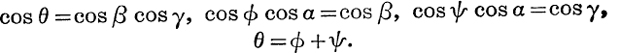
15. Eliminate θ, ϕ, ψ from
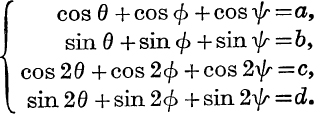
16. Eliminate α1, α2, α3, β1, β2, β3 from
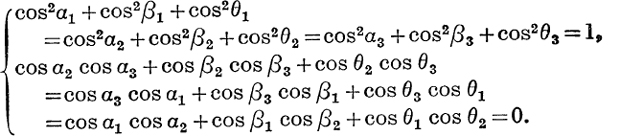
17. Eliminate l and m from
![]()
where no two of the angles α, β, γ differ by a multiple of 2π.
Also prove that l = m (cos α + cos β + cos γ).
18. If sin(ϕ + ψ) + sin(ψ + θ) + sin(θ + ϕ) = 0 and
![]()
where sin (θ + ϕ) ≠ 0, prove that λμ + λ + μ = 0.
19. Eliminate x, y, z from
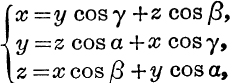
and express the result in factors.
20. Eliminate m and m′ between
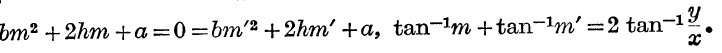
Inequalities.
Example 8. If θ1 θ2, θ3, θ4, θ5 are five positive acute angles such that their sum is 5α, find the maximum value of 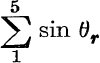 .
.
Suppose that θ1 is as large as any of the 5 angles and that θ2 is as small as any of the 5 angles, so that θ1 > α > θ2 > 0.
Then
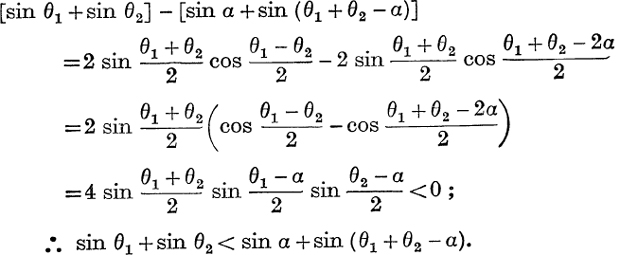
If then, in 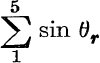 , we replace sin θ1, sin θ2 by sin α, sin (θ1 + θ2 – α), we have not altered the sum of the angles but we have increased the sum of their sines.
, we replace sin θ1, sin θ2 by sin α, sin (θ1 + θ2 – α), we have not altered the sum of the angles but we have increased the sum of their sines.
This process can be repeated until each angle is α and this stage is reached after 4 steps at most; ![]() the maximum value is 5 sin α.
the maximum value is 5 sin α.
EXERCISE XIV. f.
Discuss the maximum and minimum values of (Nos. 1-5):
1. 4 tan x + 3 cot x.
2. 1 – sin x + sin2x.
3. 5 – 4 sin x + sin2x.
4. 5 sec θ – 3 tan θ.
5. 10 sin2θ + 15 sin θ cos θ + 18 cos2θ.
6. Show that tan 3x cot x is not between 3 and ![]() .
.
7. Find the least numerical value of ![]() when a > b.
when a > b.
8. Find the maximum and minimum values of tan 3x cot3x.
9. Show that the maximum and minimum values of
![]()
are the roots of (x – a) (x – c) = b2.
Find the greatest values of the following (Nos. 10-13):
10. a cos θ + b cos ϕ, subject to θ + ϕ = α.
11. tan θ tan ϕ, subject to ![]() , and
, and  .
.
12. sin θ sin ϕ sin ψ, subject to θ + ϕ + ψ = 3α, and ![]() .
.
13. cos θ cos ϕ cos ψ, subject to θ + ϕ + ψ = 3α, and ![]() .
.
14. Find the minimum value of tan2A + tan2B + tan2C, where A, B, C are three acute angles whose sum is a right angle.
15. Find the least values of (i) ∑ tan A, (ii) ∑ cot A, (iii) ∑ cosec A, when A, B, C are positive acute angles with a constant sum 3D.
In a triangle ABC, prove the following results (Nos. 16-22):
16. 1 < cos A + cos B + cos C ≤ ![]() .
.
17. cos 2A + cos 2B + cos 2C ≥ – ![]() .
.
18. 8 cos A cos B cos C ≤ 1, and only = 1 if A =B = C.
19. cos2![]() (B – C) + cos2
(B – C) + cos2![]() (C – A) + cos2
(C – A) + cos2![]() (A – B) > 1.
(A – B) > 1.
20. tan A + tan B + tan C ≥ 3 ![]() , if the angles are acute.
, if the angles are acute.
21. 8 sin ![]() A sin
A sin ![]() B sin
B sin ![]() C ≤ 1.
C ≤ 1.
22. x2 + y2 + z2 – 2yz cos A – 2zx cos B – 2xy cos C > 0, unless
![]()
23. Prove that the least value of cos2θ + cos2ϕ + cos2ψ, subject to a cos θ + b cos ϕ + c cos ψ = d, is ![]() .
.
24. If 0 < (α, β, γ) < ![]() π, prove that
π, prove that
![]()
MISCELLANEOUS EXAMPLES
EXERCISE XIV. g.
1. Prove that sin 16° + sin 20° + sin 92° = sin 52° + sin 56°.
2. Prove that
![]()
3. Prove that ![]() .
.
4. Express sin (α + β) and cos (α + β) in terms of sin α + sin β( ≡ s) and cos α + cos β (≡ c), and prove that
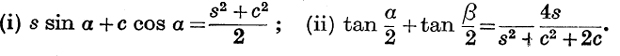
5. If 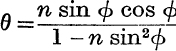 , prove that tan (θ – ϕ) = (n – 1) tan ϕ.
, prove that tan (θ – ϕ) = (n – 1) tan ϕ.
6. If e (sin ϕ – sin ϕ′) = sin(ϕ – ϕ′) and ϕ, ϕ′ do not differ by 2nπ, prove that e2 sin ϕ sin ϕ′ = (e2 – 1) cos2![]() (ϕ – ϕ′).
(ϕ – ϕ′).
7. Prove that 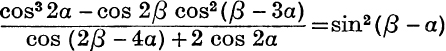 .
.
8. If 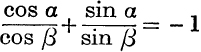 , prove that
, prove that ![]() .
.
9. If A + B + C + D = 2π, prove that
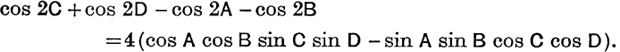
10. If c1, c2, c3, c4 are the cosines of the angles of a quadrilateral, prove that
![]()
11. Prove that
![]()
12. If 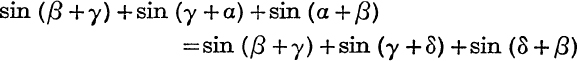 prove that α + β + γ + δ = (2n + 1)π, if the angles are essentially distinct
prove that α + β + γ + δ = (2n + 1)π, if the angles are essentially distinct
13. If cos α + cos β + cos γ = – cos α cos β cos γ prove that cosec2α + cosec2β + cosec2γ = 1 ± 2 cosec α cosec β cosec γ.
14. If 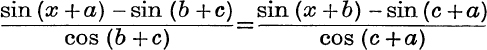 , prove that each of them is equal to the third similar expression, unless a – b = nπ.
, prove that each of them is equal to the third similar expression, unless a – b = nπ.
15. If a + b + c = 2s, prove that
![]()
16. Prove that
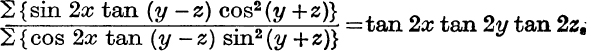
Eliminate θ in Nos. 17-24.
17. a sin θ + b cos θ = c, a cos θ – b sin θ = d.
18. 2 cos2θ + sin θ = a, 2 sin2θ + cos θ = b.
19. x cos θ + b sin θ = cos 3θ, x sin θ – y cos θ = 3 sin 3θ.
20. a sin (θ + α) + b sin (θ + β) + c sin (θ + γ) = 0
![]()
21. cos3θ + a cos θ = b, sin3ϕ + a sin ϕ = c.
22. 16 sin5θ – sin 5θ = 5x, 16 cos5θ – cos 5θ = 5y.
23. sin2θ tan α + sin2α tan θ = p, cos2θ cot α + cos2α cot θ = q.
24. 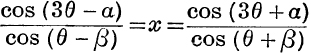 .
.
25. Find the greatest possible value of ![]() .
.
26. Prove that cot θ – cot 4θ > 2, if 0 < θ < ![]() π.
π.
27. Prove that
![]()
28. In any triangle ABC prove that ∑tan2![]() A ≥ 1.
A ≥ 1.
29. Prove that the area of the pedal triangle DEF ≤ ![]() Δ.
Δ.
30. If sin θ = μ sin ϕ, where μ > 1, and θ, ϕ lie between 0 and ![]() , prove that θ – ϕ increases when ϕ increases.
, prove that θ – ϕ increases when ϕ increases.