CHAPTER II
PROPERTIES OF THE QUADRILATERAL
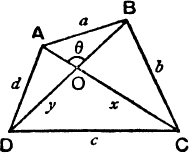
Notation. In dealing with a quadrilateral ABCD, we shall denote the angles by A, B, C, D, and shall represent the other elements (see Fig. 16), as follows :
FIG. 16.
We assume the quadrilateral to be convex.
The Cyclic Quadrilateral. If a quadrilateral is known to be cyclic, and if the lengths of the sides, in order, are given, it is possible to calculate the other elements of the figure. Formulae for S, x, y, the circumradius R, and the angles, in terms of a, b, c, d may be obtained as follows :
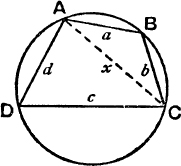
FIG. 17.
The area of a cyclic quadrilateral is
We have
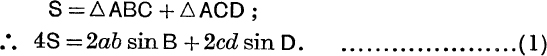
Also a2 + b2 – 2ab cos B = x2 = c2 + d2 – 2cd cos D;
From (1) and (2), by squaring and adding,
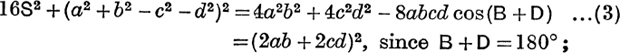
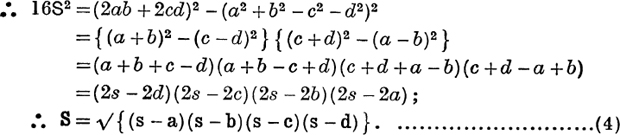
This formula was first given by the Hindu mathematician Brahmagupta (630 A.D.), but he believed, wrongly, that it held good for any quadrilateral. The Greek mathematician Hero had, however, pointed out that the general quadrilateral is not determined by the four sides alone. An n-sided polygon is determined by 2n – 3 elements—a simple framework with n joints is ‘ just stiff ’ if it contains 2n – 3 rods.
The diagonals of a cyclic quadrilateral are given in terms of the sides by the formulae
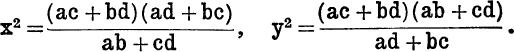
Since
and
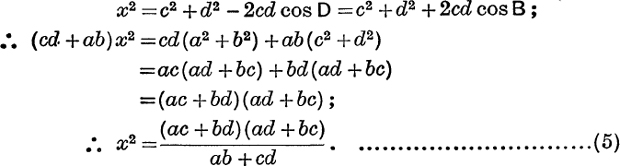
The formula for y is proved in the same way.
By multiplication, we have Ptolemy’s Theorem,
By division, we have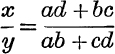 
.
The circumradius, R, is given by
Using the formula 
for a triangle, we have
∴ adding,
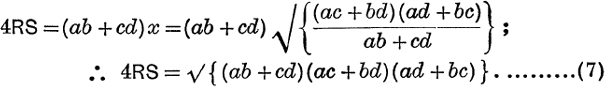
The Angles of a cyclic quadrilateral may be found from formulae like
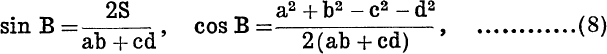
which follow from equations (1) and (2), p. 24, in virtue of B + D = 180°. From (8) it is easy to obtain
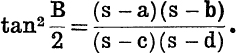
The expressions for x2 and y2 are easily remembered, if this is desired, by noting that the sides paired together in the denominator are on the same side of the required diagonal.
EXERCISE II. a.
[The results in this Exercise refer to cyclic quadrilaterals.]
1. Find the area of the cyclic quadrilateral whose sides in order are 4, 5, 6, 7.
2. With the data of No. 1, find the lengths of the diagonals x, y.
3. With the data of No. 1, find the length of the diameter of the circumcircle.
4. With the data of No. 1, find the interior angle between the sides of lengths 4, 5.
5. Prove that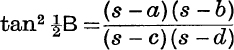 
.
6. Prove that (s – b) tan 
A = (s – d)tan B.
7. Express tan C tanD in terms of the sides.
8. Prove that S = 
tan A (a2 – b2 – c2 + d2).
9. Interpret the results obtained from the formulae for S, cos B, and R by putting d = 0.
10. Simplify the expressions for S and tan2 B when a + c = b + d. What is the geometrical meaning of this condition ?
11. The sides of a quadrilateral taken in order are 7, 4, 4, 3, and the angle between the first two is 60° ; prove that the quadrilateral is cyclic and find its circumradius.
12. From equations like a2 = AO2 + OB2 – 2AO . OB cos θ, prove that 2xy cos θ = b2 + d2 – a2 – c2, and deduce that
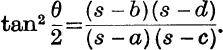
13. Prove that 
.
14. Prove that 
.
15. Express BO . OD in terms of the sides.
16. If AB, DC are produced to meet at P, and DA, CB at Q, prove that 
, and deduce expressions for QA, QB, QC, QD in terms of the sides. Write down similar expressions for PA, PB, PC, PD.
17. With the data of No. 16, prove that the other point of intersection K of the circles QAB, PBC lies on PQ, and deduce that
The General Quadrilateral. Equation (3), p. 24, is applicable to any quadrilateral, and it may be used to calculate the area. The equation may also be written
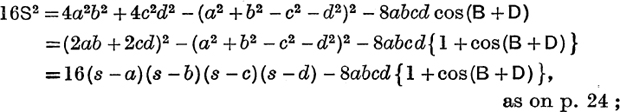
If the lengths of the sides of a quadrilateral are given, equation (9) shows that the area is greatest when cos (B + D) = 0, i.e. when B + D = 180°. Therefore the area is greatest when the quadrilateral is cyclic.
An extension of Ptolemy's Theorem. It was proved in E.T., pp. 178, 179, that
It may similarly be proved (see Ex. II. a, No. 12), that
squaring and adding,
substituting for 16S2 from equation (3),
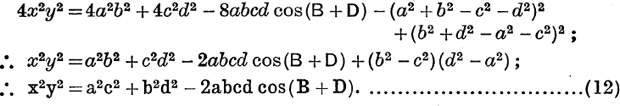
Equations (10) and (11) lead to another expression for the area. By division,
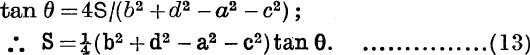
The Circumscribable Quadrilateral. This is a quadrilateral in which a circle can be inscribed.
If P, Q, R, T are the points of contact of AB, BC, CD, DA, we have
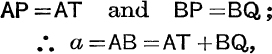
similarly
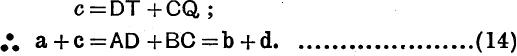
Conversely, it can be proved that, if a + c = b + d, a circle can be inscribed in the quadrilateral, see Ex. II. b, No. 8.
From (14). we have
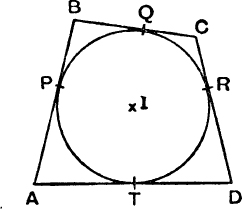
FIG. 18.
thus equation (9), p. 27, becomes
We have therefore for the area of a circum-scribable quadrilateral
If the quadrilateral is also cyclic, sin (B + D) = sin 90° = 1;
The in-radius of a circumscribable quadrilateral or polygon is 
.
For, if I is the in-centre, Δ AIB = ra, etc.;
∴ by addition,
For some properties of regular polygons, see E.T., pp. 179, 180.
EXERCISE II. b.
1. Find the sum of two opposite angles of the quadrilateral in which a = 13, b = 14, c = 12, d = 9, S = 138.
2. For the quadrilateral of No. 1, find the angle between the diagonals.
3. For the quadrilateral of No. 1, find xy.
4. If a = 7, b = 8, c = 9, d = 11, and S =33, find the angle between the diagonals.
5. If a = 7, b = 8, c = 9, d = 11, and θ = 60°, find S and xy.
6. The sides of a cyclic quadrilateral in order are 2, 4, 3, 5 ; calculate the cosine of the angle of intersection of the diagonals.
7. Explain the meaning of equation (12) when B = D = 0°, and when B = D = 180°.
8. In a quadrilateral for which a + c = b + d, where a > d, AX is cut off from AB equal to AD, and CY is cut off from CB equal to CD. Show that BX = BY and that the circumcentre of DXY is equidistant from the sides of the quadrilateral. (This proves the converse of relation (14) on p. 27.)
9. If B + D = 90°, prove that x2y2 = a2c2 + b2d2.
10. Show that the area of a circumscribable quadrilateral is (ac – bd) tan θ or (b – a)(a – d) tan θ or 
{x2y2 –(ac – bd)2}.
11. If a quadrilateral circumscribes a circle, show that the radius of the circle is 
.
12. If ABCD is circumscribable, prove that
13. If ABCD is circumscribable, prove that
14. If a + b = c + d, deduce a formula for the area from the general formula.
15. If a circle can be drawn to touch the sides of a quadrilateral when produced, obtain a relation of the form a + b = c + d.
16. The sides, in order, of a cyclic quadrilateral are 4, 3, 5 and 6. Show that the quadrilateral is also circumscribable, and find (i) its area, (ii) its in-radius, (iii) the angle between the sides 4 and 6, (iv) the lengths of the diagonals, and (v) the circumradius.
17. The sides, taken in order, of a hexagon circumscribed about a circle are 13, 12, 8, 11, 9, and x. Find x, and if the area is 60, find the radius of the circle.
18. How many elements are required, in general, to determine a pentagon ? A cyclic pentagon has sides, in order, of lengths 39, 52, 39, 25, 33 and the longest diagonal is 65, find the area.
EASY MISCELLANEOUS EXAMPLES
EXERCISE II. c.
1. The sides of a cyclic quadrilateral taken in order are 1, 3, 4, 6 ; find the largest angle.
2. Three cyclic quadrilaterals have sides 8, 9, 10, 13, in different orders. Prove that their areas and circumradii are equal, and find the lengths of their diagonals.
3. Prove that there is a quadrilateral in which a = b = y = 65, c = 50, d = 78, x = 112, and find its area. Is the quadrilateral cyclic ?
4. If a = 4, b = 1, c = 7, B = 120° = C, find d.
5. If a = l, b = 3, c = 2, A = 60°, B = 150°, find d and D.
6. When a, b, c, A, C are given, is the quadrilateral determined with or without ambiguity ?
7. If a = 7, b = 12, c = 5, A = 60°, C = 90°, find d.
8. If a = 14, b = 12, c = 5, A = 60°, C = 90°, find d.
9. If A = 90°, B = 60°, C = 150°, a = 2, b = 1, find c and d.
10. If A = 120° = B, D = 90°, a = 3, c = 5, find b and d.
11. If a2 + c2 = b2 + d2, prove that θ = 90°.
12. If A = 60° and B = 90° = D, prove that 3x2 = 4y2.
13. If ABCD is cyclic and AD is a diameter, prove that
14. If ABCD is cyclic and a – c = b – d, prove that S = bctan
. Interpret the condition geometrically.
15. If ABCD is circumscribable, prove that
16. If ABCD is both cyclic and circumscribable, prove that
17. Find the ratio of the areas of two regular polygons of n sides and 2n sides inscribed in the same circle.
18. Find the ratio of the areas of two regular polygons of n sides, inscribed in and circumscribed about a given circle.
19. The length of a side of a regular n-sided polygon is 2l, and the areas of the polygon and of the inscribed and circumscribed circles are A, B, C ; prove that C – B = πl2 and n2l2B = πA2.
20. Prove that the ratio of the areas of two regular polygons of n sides and 2n sides and of equal perimeters is
21. If rn and Rn denote the in-radius and circumradius of a regular n-sided polygon of given perimeter, prove that
22. If a square and a regular hexagon have equal perimeters, prove that the ratio of their areas 
.
HARDER MISCELLANEOUS EXAMPLES
EXERCISE II. d.
1. Do equations (9) to (13) require any modification for the quadrilateral in Fig. 19 ?
FIG. 19.
2. Two quadrilaterals ABCD, A′B′C′D′ of equal area, but not congruent, have their corresponding sides equal; also B = D′ = 90° ; prove that ab = cd.
3. If a = 24, b = 7, c = 65, d = 60, x = 25, find S, y, D.
4. If a = 13, b = 14, c = 12, d = 9, S = 138, show that
91 cos B – 54 cos D = 35 and 91 sin B + 54 sin D = 138.
Hence prove that 138 sin D – 35 cos D = 138 and find D. Show also that x = 15 or x = 
18·1.
5. Fig. 20 represents a “crossed ” cyclic quadrilateral. What meaning must be given to S and what other conventions should be introduced to enable equations (1), (2), (3) on p. 24 to remain true ? Obtain a result corresponding to equation (4).
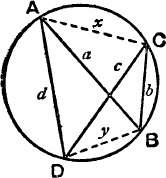
FIG. 20.
6. With the data of Fig. 20, find x and y in terms of a, b, c, d. Show that 4 rods of lengths 8, 9, 10, 13 cannot be fitted together in any order to form a crossed cyclic quadrilateral.
7. If ABCD is cyclic and if AB, DC, when produced, cut at right angles, prove that (ab + cd)2 + (ad + bc)2 = (b2 – d2)2.
8. If ABCD is cyclic and if ac = bd, prove that the tangents at A and C meet on BD. Conversely, if the tangents at A, C meet on BD (i.e. if ABCD is a harmonic system of points on a circle), prove that
9. A quadrilateral is inscribed in a given circle of radius R, and one side subtends a given angle a at a point of the arc of the circle on the opposite side to the quadrilateral. Prove that the greatest possible area of the quadrilateral is 2R2 sin3
.
10. If the sides of a cyclic quadrilateral are the roots of
express S in terms of p, q, s, t.
11. In a cyclic quadrilateral, prove that the productions of AB, DC meet at an angle ϕ, given by
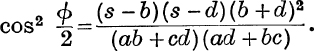
12. Discuss the different ways in which a quadrilateral may be determined by five of the eight elements (4 sides, 4 angles), showing in which cases more than one quadrilateral may exist.
13. In any quadrilateral, prove that
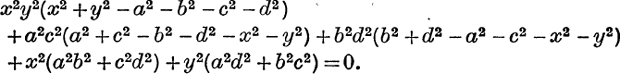
14. If ABCD is circumscribable, and α, β, γ, δ are the lengths of the tangents from A, B, C, D, prove that
15. Prove that the distance between the circumcentres of ADC and BDC is asin (B +D) cosec C cosec D.
16. If R and r are the circumradius and in-radius of a quadrilateral and if z is the distance between the centres of the circles, prove that 
. corresponding result for a triangle.
[If I is the in-centre, let AI, CI meet the circumcircle in A′, C′; use AI . IA′= R2 – z2 = CI . IC′ to find IA′, IC′, and substitute in
17. Prove that the necessary and sufficient condition for the existence of a crossed cyclic quadrilateral with sides of lengths a, b, c, d in that order of magnitude is b + c > a + d. For a = 13, b = 12, c = 11, d = 6, find x and y.
18. A hexagon is inscribed in a circle of radius R; alternate sides are of lengths l, m; prove that 3R2 = l2 + lm + m2.
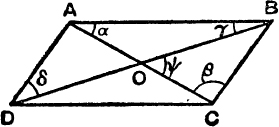
FIG. 21.
19. In Fig. 21, ABCD is a parallelogram. Prove that
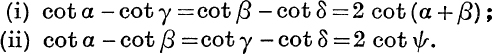
20. If Pn and P′n are the perimeters of regular n-gons inscribed and circumscribed to the same circle, prove that
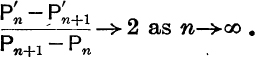
21. The base of a pyramid is a horizontal regular n-gon, and its vertex is at height h vertically above the centre of the base. If a is the circumradius of the base and 2θ the angle between two adjacent sloping faces, prove that
