

 |  |
Vectors are objects that you can add together to make new vectors, and they can be multiplied by scalars to make new vectors as well. Vectors are points located in a finite space. While you may not view your data as a vector, they are great ways to represent numeric information.
If you are dealing with ages, heights, and weights of a large group of people, you could treat this data like three-dimensional vectors: age, weight, height. If you are teaching a class that has four exams throughout the semester, you could treat these grades like a four-dimensional vector: test1, test2, test3, test4.
One of the easiest from-scratch approaches is to show your vectors as a number list. This list of three numbers will correspond to a single vector in your three-dimensional space, and so on:
“ height_weight_age = [70,
170,
40 ]
Grades = [95,
80,
75,
62 ] “
A problem that comes with this approach is that you are going to want to do arithmetic on your vectors. Since Python lists don’t work as vectors, and as such don’t give you any tools for vector arithmetic, you will have to create these types of tools yourself. Let’s see how that would work.
To start out, you will need to add in two vectors. Vectors will add component-wise. This means that if there are two vectors, a and b, and they have the same length, they have a sum that has a first element of a[0] + b[0], and a second element of a[1] + b[1], and so on. If they don’t have the same length, then they can’t be added in.
If you were to add in the vectors [2, 3] and [3, 2] you would get [2 + 3, 3 + 2] or [5, 5].
This can easily be used by zipping all of the vectors together and then make use of a comprehension to add in all of the corresponding elements.
“ def vector_add(a, b):
Return [a_i + b_i
For a_i, b_i in zip (a, b)] “
In a similar manner, you can subtract your two vectors by getting rid of the corresponding elements.
“ def vector_substract(a, b):
Return [a_i – b_i
For a_i, b_i in zip (a, b)] “
There may be times when you need to sum a vector list. This means that you will want to make a new vector which is the sum of all the first elements, and the second vector is the sum of the second elements, etc. The simplest way for you to figure this out is to add a vector at a time
“ def vector_sum (vectors) :
Result = vectors[0]
For vector in vectors [1:] :
Result = vector_add(result, vector)
Return result “
When you really think about what we are doing, we are only reducing the vector list with vector_add. This means that we are able to rewrite this using higher-order function, such as:
“ def vector_sum(vectors) :
Return reduce(vector_add, vectors) “
Or you could:
“ Vector_sum = partial(reduce, vector_add) “
This last one is probably cleverer instead of helpful. Next, you will also have to multiply your vector by your scalar, which can be done by multiplying every vector element by this number.
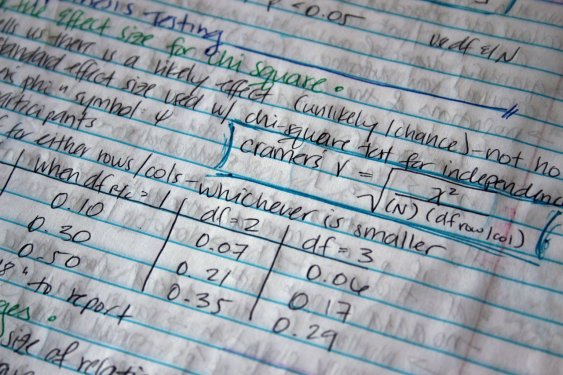
“ def scarlar_multiply (c, a):
Return [c * a_i for a_i in a] “
This is going to give you the ability to compute the componentwise means of your same-sized vector lists.
“ def vector_mean(vectors):
N = len(vectors)
Return scalar_multiply( 1/n, vector_sum (vectors)) “
One of the lesser known tools is to use the dot product. This product is created through the sum of two vectors and their componentwise products.
“ def dot(a, b):
Return sum(a_i * b_i
For a_i, b_i in zip(a, b)) “
This product will measure how far vector a will extend in vector b’s direction. One example would be if b = [1, 0] then dot (a, b) is only the first element of a. A different way to do this is by saying it is the length of the vector you would see if you were to project point a on point b.
When you use this, it is quite easy to find a vector’s sum of squares.
“ def sum_of_squares (a):
Return dot (a, a) “
And this can then be used to figure out the length or magnitude
“ import math
Def magnitude(a):
Return math.sqrt(sum_of_square(a)) “
At this point you now have the pieces you need to figure out space between your two vectors, as you can see in this equation:
![]()
“ def squared_distance(a, b) :
Return sum_of_squares( vector_subtract (a, b))
Def distanc(a, b) :
Return mathsqrt(squared_distance(a, b)) “
You can write the equivalent to get a clearer image of what we’re looking at.
“ def distanc(a, b) :
Return magnitude( vector_substract (a, b)) “
This is a pretty good amount of information to help you get started with vectors. It’s important that you take the time to study them even further if you are still unsure how it works.
Note: When it comes to using lists as vectors, it works well for exposition, but not for performance. When it comes to production code, you want to use NumPy library. This library includes all of the high-performance array class, and it includes all of the arithmetic operations.