15.1 Introduction
Accidents by industrial radiography sources, which usually involve powerful gamma-emitting sources, could result in very high radiation doses to workers, leading to serious injuries or even death [1]. Even members of the public could be accidentally irradiated by such sources when the sources are not properly controlled or regulated. Moreover, industrial radiography accidents are one of the most frequently reported accidents among all reported cases in nuclear-related industries [2]. According to Lima et al. [3], a total of 80 industrial radiography accidents involving 120 workers and 110 members of the public, including 12 deaths, were recorded globally between 1896 and 2014.
Radiation accidents could lead to high radiation doses, which could induce acute radiation syndrome (ARS ); these are primarily classified into hematopoietic (0.2–2 Gy), gastrointestinal (6–10 Gy), and cerebrovascular (>10 Gy) syndromes [4]. For the effective management of patients (i.e., exposed individuals) with ARS, initial medical triage should be performed accurately and rapidly, whereby those patients who could develop symptoms should be separately identified from those who do not require medical intervention [5]. Therapies for ARS, such as dose mitigators, should be promptly administered during the latent period in which the exposed person still feels well, i.e., before symptoms occur [6]. For this purpose, it is essential not only to carefully document clinical signs and symptoms but also to accurately and quickly estimate radiation doses to exposed individuals [7].
Individual radiation doses can be estimated using various dosimetric techniques based on biological, physical, and computational approaches. However, all the existing dosimetry techniques have limitations and none of them can be used as a stand-alone tool in a satisfactory manner for most radiation accident scenarios [8]. For instance, biological or physical dosimetry techniques generally require more than several days for sample collection and analysis, and these time-consuming processes make it difficult to perform timely medical triage. These techniques are therefore impractical, especially for use in a large-scale accident involving many individuals [5, 6, 9, 10]. Moreover, these techniques are generally limited to estimating the whole-body dose, without information on organ/tissue doses or dose distributions [8]. It should be noted that information about the whole-body absorbed dose is insufficient, particularly for partial-body or localized exposures. Organ/tissue absorbed doses and/or absorbed dose distributions can be estimated from computational dosimetry approaches (e.g., Monte Carlo simulations with computational human phantoms) if reliable information on the accident scenario is available, including accurate source geometry and duration of exposure [11], which are often unclear in accident situations [8, 12]. No single technique fully meets the criteria of an ideal dosimetry technique for use in accident situations; therefore, an integrated approach using multiple dosimetry techniques is considered the best strategy [8, 13, 14]. Absorbed doses calculated with computational human phantoms could be used as one of the dose estimators, particularly as an “initial, rapid estimator.”
In the present study, a comprehensive set of organ/tissue absorbed dose coefficients (DCs) for industrial radiography sources was obtained by Monte Carlo simulations with the adult male and female mesh-type reference computational phantoms (MRCPs ) recently developed by Task Group 103 of the International Commission on Radiological Protection (ICRP ) [15]. In addition, adult male and female non-reference computational phantoms that represent the 10th and 90th percentiles of the Caucasian population were also used. These phantoms were constructed by deformation and modification of the MRCPs [16]. Note that for dose estimation of individuals in accident situations, consideration of the reference person would be insufficient, particularly when the body size of the individual involved in the accident is significantly different from that of the reference person. In this case, the dose estimation could be better approximated by using DCs calculated with a non-reference computational phantom whose body size is close to that of the actual individual.
The phantoms were implemented into the Geant4 Monte Carlo code [17] to calculate DCs by simulating the most commonly used industrial radiography sources, i.e., 192Ir and 60Co, for various source locations. The behavior of the calculated DCs was investigated, primarily by comparing the DCs among the different body size phantoms to study the influence of body size on the DCs.
15.2 Material and Methods
15.2.1 Mesh-Type Computational Phantoms
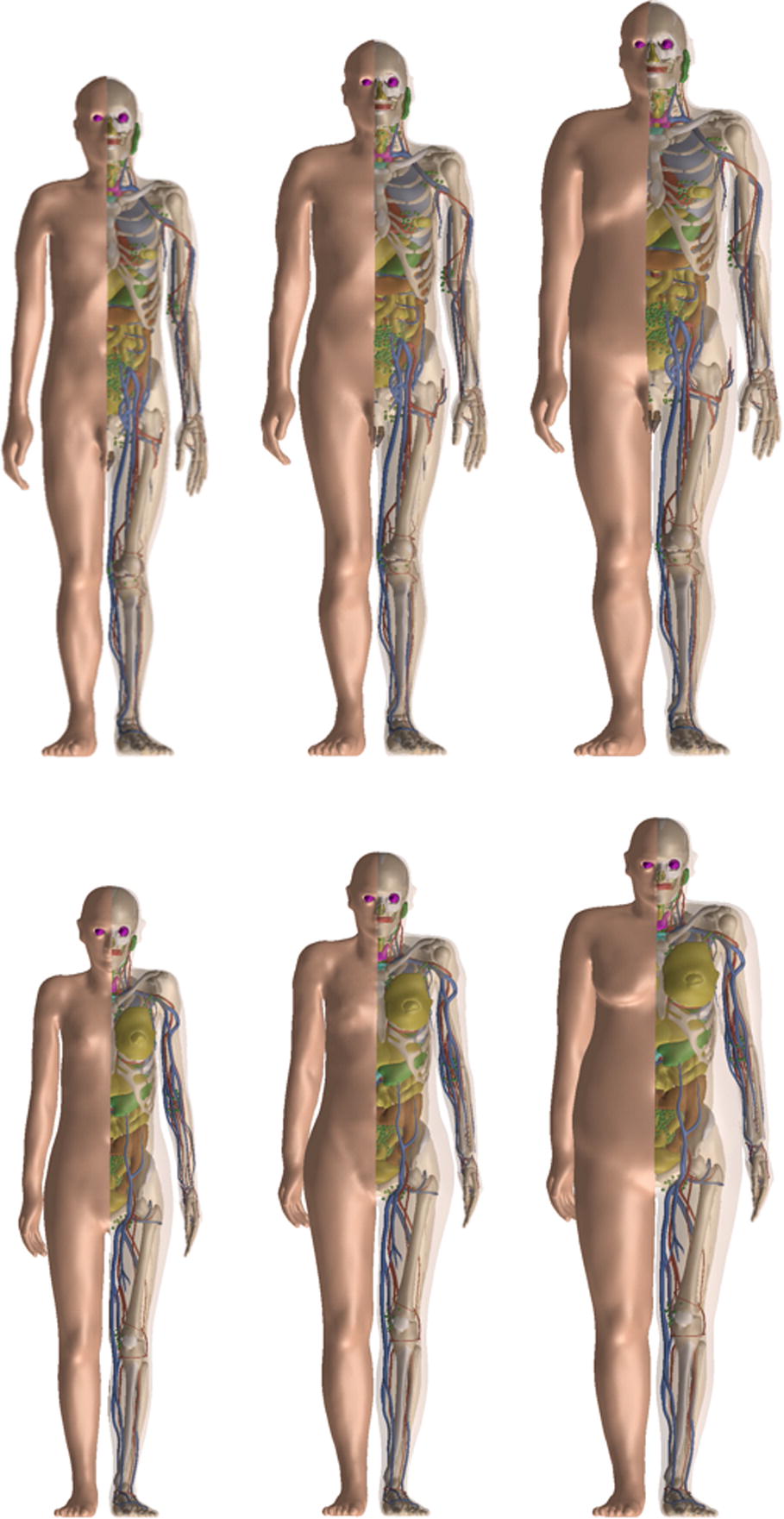
10th percentile (left), mesh-type reference computational phantoms (MRCPs ) (middle), and 90th percentile (right) phantoms for an adult male (upper figure) and adult female (lower figure)
The MRCPs represent the adult reference male and female, as established in ICRP Publication 89 [21] with respect to the reference standing height, body mass (male: 1.76 m and 73 kg; female: 1.63 m and 60 kg) and individual organ and tissue masses. The 10th and 90th percentile phantoms were constructed by Lee et al. [16], by selectively deforming and modifying the MRCPs. The 10th percentile phantoms, which represent small statures, have the 10th percentile standing height and 10th percentile body mass (male: 1.67 m and 56 kg; female: 1.55 m and 44 kg), with organ masses ~25% lighter than those of MRCPs. The 90th percentile phantoms, which represent large statures, have the 90th percentile standing height and the 90th percentile body mass (male: 1.86 m and 108 kg; female: 1.72 m and 94 kg), and organ masses ~25% heavier than those of MRCPs.
15.2.2 Calculation of Organ Absorbed Dose Coefficients for Industrial Radiography Sources
The most commonly used industrial radiography sources of the 192Ir and 60Co radioisotopes were simulated as point sources placed near the phantoms. 192Ir emits gamma rays up to 0.820 MeV with mean energy of 0.377 MeV, whereas 60Co emits 1.33 and 1.17 MeV gamma rays. The point sources were assumed to be located at three different distances (0.005, 0.1, and 0.3 m) in four directions (anterior, posterior, right lateral, and left lateral) and at five locations along the height of the phantom (ground, middle thigh and lower, middle, and upper torso). In addition, for the lower torso level, three longer distances (1, 1.5, and 3 m) were considered for the four directions. The source distances used in the calculations are the distances from the phantom surface to the sources, except for the anterior and posterior directions at the ground and middle thigh levels, for which the source distances were measured from the center of an imaginary segment tangent to the surfaces of feet or left and right legs at the given level.
The doses of organs/tissues were calculated as organ/tissue-averaged absorbed dose per radioactive decay (Gy s−1 Bq−1), by using the Geant4 Monte Carlo code [17]. For the simulations, we used a range cut of 5 μm for secondary electrons and photons, and the Livermore physics model ( G4EmLivermorePhysics ), which is provided by Geant4 for the transportation of electrons and photons with the energies ranging from 250 eV to 1 GeV. The statistical errors of the calculated values were less than 5% for all cases. The red bone marrow (RBM) DCs were calculated by using the fluence-to-absorbed dose response functions provided in Annex D of ICRP Publication 116 [22] in order to consider the microscopic structure of bone geometry for different skeletal regions.
Note that the DCs in the present study (assuming point sources) were calculated without considering the exact source geometry. In order to allow users to consider the self-shielding effect of the sources, source self-shielding factors were additionally calculated by investigating the ratio of DCs for the spherical volume sources enclosed by capsule material to those for the bare point sources. For this purpose, combinations of four different thicknesses of radioactive material (1, 2, 3, and 4 mm) and two different thicknesses of capsule wall (1 and 2 mm) were considered, which cover the geometries of most radiography sources. The composition of the capsule material was assumed to correspond to that of 316 L stainless steel.
15.3 Results and Discussion
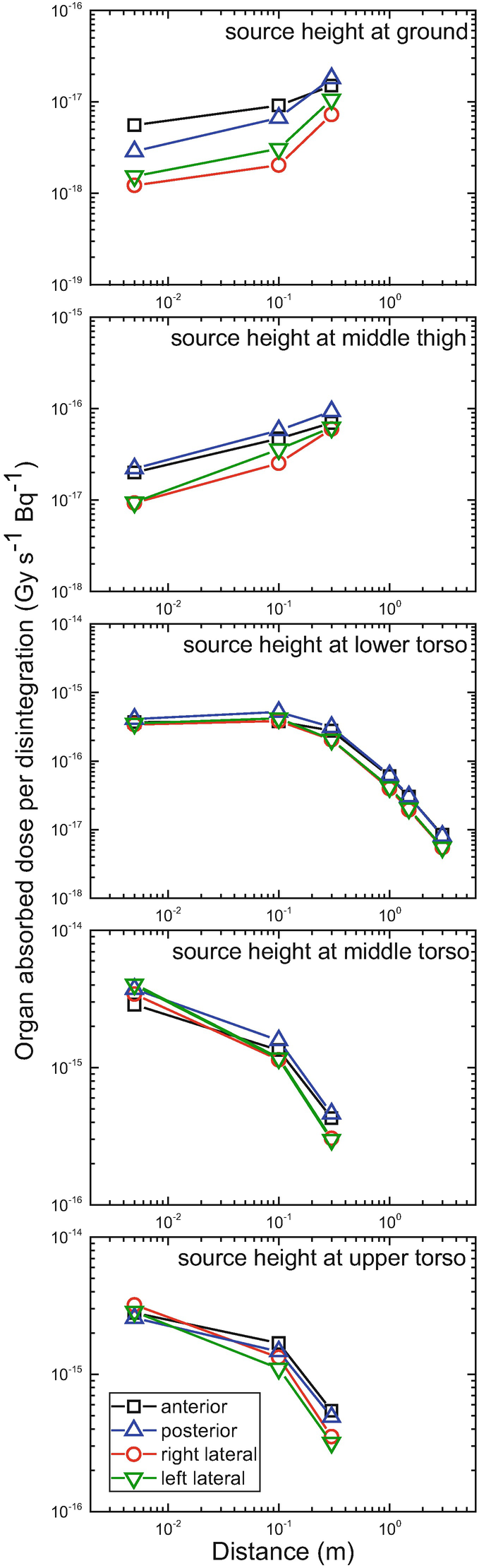
Lungs absorbed dose coefficients for the adult male mesh-type reference computational phantom as a function of distance from the phantom surface, for a point source of 60Co placed in four different directions (anterior, posterior, right lateral, and left lateral) and at five different heights (ground, middle thigh and lower, middle, and upper torso)
Our analysis also showed that the DC difference due to different body sizes tends to be larger when the source is closer to the body. When the source distance is shorter than 1 m, in general, the DCs of the 90th percentile phantoms were significantly smaller than those of the MRCPs; the maximum difference was a factor of ~8 for the female brain for the 192Ir source located at 0.3 m from the phantom surface in the right-lateral direction at the ground level. The DCs of the 10th percentile phantoms were significantly larger than those of the MRCPs; the maximum difference was 2.3 times for the female brain for the 192Ir source located at 0.1 m from the phantom surface in the left-lateral direction at the ground level. It should be noted that, for both cases, maximum differences were not found at the shortest source distance (0.005 m), because in these cases the source particles could directly reach the head only for the smaller phantoms, while this was not the case for the other phantoms.

Large intestine absorbed dose coefficients for the adult male mesh-type reference computational phantom (black squares) as a function of distance from the phantom surface, for a point source of 192Ir in four different directions (anterior, posterior, right lateral, and left lateral) at the height of the lower torso level, along with those of the 10th percentile adult male phantom (red circles) and the 90th percentile adult male phantom (blue triangles)
Finally, the DCs of MRCPs were generally found to be closer to the DCs of 10th percentile phantom than those of 90th percentile phantom. This is mainly because the MRCPs do not exactly correspond to the 50th percentile in body weight; the adult male and female MRCPs correspond to ~30th and ~40th percentile in body weight, respectively, which are closer to 10th percentile than 90th percentile. It can also be seen that the body size effect tends to be less significant for sources in the posterior direction as opposed to those in the other directions (anterior and left and right laterals). This can be explained by the fact that the change of the residual soft tissue (i.e., adipose tissue) among the different body size phantoms in the back is smaller than that in the other sides, especially in the abdominal region [23–25].
Source self-shielding factors for 192Ir and 60Co
Capsule-wall thickness | Radioactive material thickness | |||||||
|---|---|---|---|---|---|---|---|---|
1 mm | 2 mm | 3 mm | 4 mm | |||||
192Ir | 60Co | 192Ir | 60Co | 192Ir | 60Co | 192Ir | 60Co | |
1 mm | 0.840 | 0.972 | 0.717 | 0.965 | 0.627 | 0.958 | 0.556 | 0.949 |
2 mm | 0.803 | 0.953 | 0.694 | 0.947 | 0.606 | 0.938 | 0.536 | 0.929 |
15.4 Conclusion
In the present study, a comprehensive data set of organ absorbed dose coefficients (DC) for industrial radiography sources of two radioisotopes (192Ir and 60Co), placed in 72 different source locations were obtained by performing Monte Carlo simulations with the mesh-type reference computational phantoms (MRCPs ) and 10th and 90th percentile phantoms. In addition, the characteristics of the DC data were investigated, thereby finding that the body size indeed significantly influences the DCs, especially when the sources are closer than 1 m to the human body, which is often the case for accidents involving industrial radiography sources. The DC data are expected to be used as an initial tool for the rapid dose estimation of individuals accidentally exposed to industrial radiography sources. A full set of the DCs will appear in a forthcoming ICRP Publication prepared by the ICRP Task Group 103 of Committee 2.
Acknowledgments
The authors would like to thank Dr. Wi-Ho Ha and Mr. Han Sung Kim of Korea Institute of Radiological & Medical Sciences (KIRAMS) for helpful discussions. This work was supported by the Nuclear Safety Research Development (NSR&D) Program through Korea Foundation of Nuclear Safety (KoFONS), funded by the Nuclear Safety and Security Commission (NSSC), and additionally by the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT and Future Planning (Project No.: 1705006, 2016R1D1A1A09916337). Two of the authors (Haegin Han and Chansoo Choi) were supported by the Global Ph.D. Fellowship program (Project No.: NRF-2018H1A2A1059767 and NRF-2017H1A2A1046391).

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.