© The Author(s) 2019
S. Makarov et al. (eds.)Brain and Human Body Modelinghttps://doi.org/10.1007/978-3-030-21293-3_5

5. Design and Analysis of a Whole-Body Noncontact Electromagnetic Subthreshold Stimulation Device with Field Modulation Targeting Nonspecific Neuropathic Pain

Sergey Makarov1, 2  , Gene Bogdanov3, Gregory Noetscher2, William Appleyard3, Reinhold Ludwig3, Juho Joutsa4, 5, 6 and Zhi-De Deng7
(1)
Massachusetts General Hospital, Boston, MA, USA
(2)
Worcester Polytechnic Institute, Worcester, MA, USA
(3)
ECE Department, Worcester Polytechnic Inst, Worcester, MA, USA
(4)
Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Harvard Medical School, Charlestown, MA, USA
(5)
Department of Neurology, University of Turku, Turku, Finland
(6)
Division of Clinical Neurosciences, Turku University Hospital, Turku, Finland
(7)
Noninvasive Neuromodulation Unit, Experimental Therapeutics & Pathophysiology Branch, National Institutes of Mental Health, NIH, Bethesda, MD, USA
 
 
Sergey Makarov
Email: makarov@wpi.edu

Keywords

Electromagnetic stimulationModulationNeuropathic pain reliefLow back painChronic painTENSSafety

5.1 Introduction

Pain is distinguished by duration as acute (less than 6 weeks), subacute (6–12 weeks), and chronic (12 weeks or more) pain. Approximately 100 million US adults suffer from common chronic pain conditions, more than the number affected by heart disease, diabetes, and cancer combined [1]. The economic cost of chronic pain in adults, including health care expenses and lost productivity, is $560–630 billion annually [1]. Seven in ten Americans feel that pain research and management should be one of the medical community’s top few priorities (16%) or a high priority (55%) [2].

One form of chronic pain is nociceptive pain, which is the normal response to injury of tissues such as muscles, visceral organs, joints, or bones. Another form is neuropathic pain, which involves dysfunction of (i) the peripheral nervous system (PNS) or (ii) the central nervous system (CNS). The latter case is amplification and generation of pain within the CNS itself due to distorted sensory processing, malfunctioning of pain-inhibitory mechanisms, and enhancing pain-facilitatory mechanisms [3–6]. An example is psychogenic pain, which does not usually have a physical origin [7, 8]. Highly prevalent symptoms in chronic pain are depression and anxiety [7–11], which are reported by more than 50% of patients with chronic pain [9]. Pain and depression may create a vicious cycle in which pain worsens depression and vice versa [10].

Low back pain, either acute or chronic, dominates other pain types [7] and affects about 80–84% of the population at least once at some point in life [12–14]. In the US Armed Services alone, low back pain was the primary diagnosis for more than seven million ambulatory care visits between 2000 and 2009 [15]. Current estimates are that approximately 25% of people with acute low back pain experience recurrent episodes, while 7–10% progress to a chronic state [15] and can experience significant physical, psychological, and social sequelae that affect their long-term functioning and quality of life [16]. According to [11], 70% of subjects with chronic low back pain report fatigue and 18% report depression. According to [17], 59% of the patients with chronic low back pain report poor sleep.

Chronic low back pain accounts for 22% of all chronic pain cases and for 35% of most persistent pain sites [7]. The classification of low back pain is complicated by the varying presentation and complex nature of pain [14]. The most common diffuse neuropathic pain without radiating beyond the buttocks is classified as nonspecific low back pain [14], which makes up 60% of individuals suffering from chronic low back pain [18].

The initial treatment for acute nonspecific low back pain is conservative, including nonopioid analgesics (acetaminophen, aspirin), nonsteroidal anti-inflammatory drugs (ibuprofen, ketoprofen), physiotherapy, dynamic strengthening exercises, thermotherapy, and, if necessary, a short course of muscle relaxants [13, 14]. Further, conservative methods include traction treatment, manual therapy, and transcutaneous electrical nerve stimulation (TENS) [14]. A commonly prescribed treatment for chronic pain is opioids (codeine, oxycodone, hydrocodone, and morphine) [13, 19]. The use of opioids is controversial due to severe addiction and misuse [13, 15, 16, 20, 21]. It is argued that chronic use of opioids is detrimental to people with back pain because they can aggravate depression, leading to a worsening of the pain [13]. Whenever possible, opioid medications in chronic noncancer pain should be avoided [20].

TENS is a common drug-free alternative treatment technique that stimulates selected sensory nerves and muscles via electrodes placed on the skin over the painful area [22–28]. The electrodes inject electric currents and, most importantly, electric fields into body. The theory is that the local electric field stimulation can modify both cause and perception of chronic pain. A number of systematic reviews of the effect of TENS on various painful conditions, such as labor pain, rheumatoid arthritis, phantom limb pain, and chronic lower back pain, are available [22, 24–28]. However, these reviews indicate that most controlled randomized clinical trials failed to show significant effects of the existing small-scale TENS systems with a strongly localized electric field distribution.

This design-based study is driven by the limitations of TENS. We introduce a conceptually different electromagnetic stimulation device. Instead of local high-intensity and suprathreshold TENS, we suggest to stimulate the PNS and muscular system of the entire lower body in a noncontact, patient-friendly way. At the same time, we suggest to use low or subthreshold power levels. In other words, we propose mild yet more broad electromagnetic treatment, potentially beneficial for nonspecific chronic pain. The proposed device [29, 30] would primarily affect peripheral nerves, the spinal cord, muscles, joints, and bone. Simultaneously, it could influence the somatosensory cortex via many affected pathways, in line with the modern concept of central control of pain [8]. Based on the numbers cited above [7, 14, 18], we can estimate that some 14% of all chronic pain cases might be subject to the proposed alternative treatment.

The text is organized as follows. Section 5.2 describes a theoretical device model, specifies the field distribution within the resonator, and describes hardware design, test, and functionality, including semiautomatic operation/tuning and representative continuous run times. Section 5.3 provides computational results for the electric field distribution within the body obtained via two independent numerical methods. Section 5.4 discusses possible device modifications, as well as potential application scenarios. Section 5.5 concludes the chapter.

5.2 Materials and Methods

5.2.1 Suprathreshold Versus Subthreshold Stimulation

The vast majority of transcutaneous electrical nerve stimulation (TENS) devices [14, 22–28] today are suprathreshold. They excite local currents/electric fields that are strong enough to produce an action potential in peripheral axons assembled in bundles of sensory nerve fibers. A case in point is a small pulsed-current InTENSity™ Twin Stim® III device [31] similar to that shown in Fig. 5.1a [32], intended for home use. It creates a prominent zapping sensation when the electrodes are connected to the lower back. The majority of PEMF (pulsed electromagnetic field) devices operate in a similar fashion.
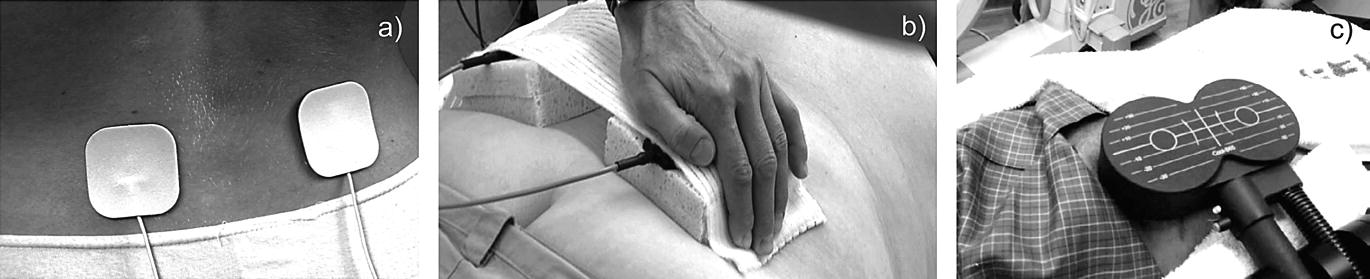
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig1_HTML.jpg
Fig. 5.1

(a) Portable pulsed-current TENS (or PEMF) device from National Health Service (NHS) England website [32]. (b) Stationary continuous-current TENS device with sponge electrodes for low back pain treatment in Hannover, Germany [33]. (c) Induction coil-based peripheral neuropathic pain stimulation for low back pain treatment [34, 35]

Alternatively, a continuous current injection with a more powerful stationary device may be employed by chiropractors as shown in Fig. 5.1b [33]. When connected to the lower back, it creates a rather strong burning sensation. The electric field may also be injected via a noncontact induction coil [34, 35] as in Fig. 5.1c. Although a broader coverage with many electrodes is now possible, local suprathreshold effects still dominate.

With respect to treatment-persistent depression, only three nonpharmacological therapies have been approved by the FDA to date; all of them are electromagnetic and suprathreshold: transcranial magnetic stimulation [36], vagus nerve stimulation [37], and electroconvulsive therapy [38].

Subthreshold refers to a low-power electromagnetic stimulation that is too small to elicit action potentials. However, it still alters the axonal membrane potential [39]. This effect accumulates and maximizes toward axon terminals, i.e., synapses [39]. It is synaptic efficacy (or natural neurotransmission efficacy) that is altered and enhanced by the subthreshold stimulation [39]. In a chain of neurons, this stimulation could cause an incremental relay effect, which may further enhance neuronal network activity [39]. The theory of subthreshold stimulation [39–42] has been developed in application to transcranial current stimulation [39–47]. Low-field magnetic stimulation of depression is an active area of research [48–54]. The subthreshold technique is also a modern research direction in spinal cord stimulation [55–59], as it eliminates noxious and off-target paresthesia, while being efficient, as well as in vagus [60], occipital [61], proximal [62], and parasympathetic [63] nerve stimulation, and in neuromuscular stimulation [64]. Electrocutaneous subthreshold stimulation has been found to improve sleep and reduce reactive anxiety/depression [65].

5.2.2 Concept of the Magnetic Stimulator. Two-Dimensional Analytical Solution for Solenoidal E-Field

Figure 5.2 shows the anticipated device concept. An external, uniform, rotating (or circularly-polarized) magnetic flux density B with amplitude B0 is created in the transverse plane around a tissue volume, depicted in Fig. 5.2a. By Faraday’s law of induction, this field excites an axial, rotating solenoidal electric field E in free space or in a tissue volume, which is expressed in terms of the magnetic vector potential A,
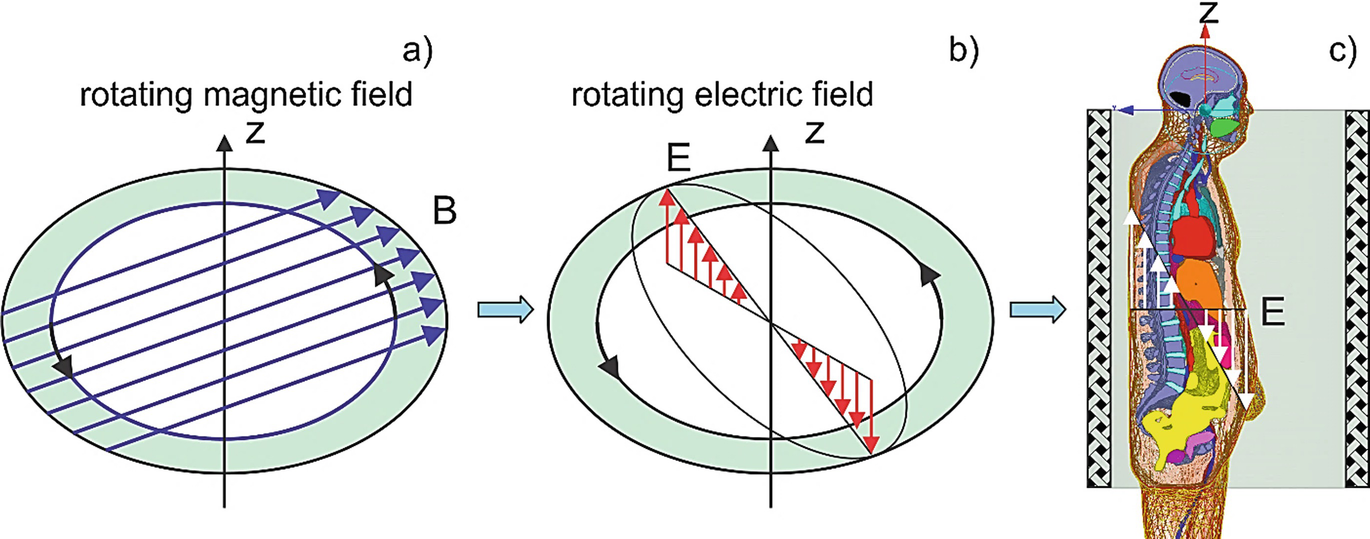
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig2_HTML.png
Fig. 5.2

Concept of non-invasive electric field excitation via the induction mechanism. A rotating magnetic field shown in (a) excites the rotating electric field within the conductor (b) and within the body (c), respectively

$$ E=-\raisebox{1ex}{$\partial A$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right. $$
(5.1)
as shown in Fig. 5.2b; we set B =  ∇  × A. Thus, when a biological body is placed into this volume, a significant noninvasively excited electric field in the axial direction will appear parallel to the major peripheral nerves, spinal cord, long bones, major arteries, veins, and other structures. This is in contrast to a solenoidal coil wound around the body creating electric fields and currents in the less desirable transverse plane.

The rotational character of the field also assures that not only one body cross section (e.g., coronal or sagittal) will be subject to the electric field excitation, but the entire body volume.

In the ideal, two-dimensional case and for any conducting target with a strict cylindrical symmetry placed into the device, either homogeneous or not, the corresponding two-dimensional problem, shown in Fig. 5.2a, b, will have an exact analytical solution in the quasi-static (or eddy current) approximation. The electric field within the target is given by [66].

$$ {E}_x=0,\kern1em {E}_y=0,\kern1em {E}_z=\omega {B}_0r\cos \left(\omega t-\phi \right) $$
(5.2)
$$ J=\sigma E $$
(5.3)
where r is the radial distance from the coil axis in cylindrical coordinates, ω is the angular frequency, ϕ is an arbitrary phase, J is induced current density, and σ is the (local) medium conductivity which is either constant or obeys cylindrical symmetry. Although Eqs. (5.2) and (5.3) might be used to roughly estimate the electric field in the body based on a cylindrically symmetric assumption, its actual value will deviate as shown below.

5.2.3 Three-Dimensional Coil Resonator Design. Solenoidal E-Field

The external rotating magnetic flux density B is created using a volumetric resonator in the form of a low-pass birdcage coil. Resonators of this type (called “birdcage coils”) are routinely used as MRI radio frequency (RF) coils [67, 68], but for a completely different purpose, namely atomic spin excitation and RF signal acquisition. The resonant frequency in this application is very high, typically 64 MHz (for 1.5 T magnets) or higher. For our purpose, we decided to reconstruct that design for a much lower frequency band of 100 kHz or less. In particular, the band of 10 kHz has recently demonstrated great promise for spinal cord stimulation for back and leg chronic pain management [55–59, 69–77] with and without previous back surgeries [70, 72], and is utilized by TENS [78]. In addition to superior pain relief, the 10 kHz band may provide long-term improvements in quality of life and functionality for subjects with chronic low back and leg pain [77]. On the other hand, a wider band of 4–30 kHz has been used for polyneuropathy (a general degeneration of peripheral nerves that spreads toward the center of the body) electrostimulation treatment [79–82].

We chose the birdcage coil because it can produce a very homogeneous B-field in the transverse plane, and because it can produce a circularly polarized B-field. These features relax the requirements for accurate patient positioning relative to the coil. The patient has significant freedom of movement transversely within the coil, including freedom of rotation (thanks to circular polarization). This should enhance patient comfort and permit long treatment sessions.

The resonator concept will allow for an arbitrary “tonic” modulation [30] of the carrier frequency, which was found to beneficially address the variable nature of chronic pain across different patients [76]. This modulation can be either open- or closed-loop (e.g., a single-channel EEG signal fed back to the modulator).

When the resonant frequency becomes low as in the present case, the standard RF birdcage coil will possess very low inductance L. Tuning such a coil toward resonance at low frequencies would require large capacitance C. This, however, means a low Q-factor (quality factor $$ Q=\sqrt{L/C}/R $$ is the “gain” of the series resonator) and higher costs, as well as higher fabrication complexity [83, 84], and will restrict the use of the conventional birdcage coil to frequencies above at least a few megahertz. Different methods to overcome this difficulty have been suggested [83–88], but they are all limited to small-size coils.

Our design described in the subsequent patent application [29] utilizes a unique large-scale low-pass birdcage coil topology with an intentionally very large number (144) of long rungs (boosting inductance) and bridging capacitors seen in Figs. 5.6 and 5.7. After this point, the improvement in adding more rungs is small. Several other reasons for the number of rungs include:

  • To distribute the required capacitors uniformly around the coil circumference

  • To improve the mechanical stiffness of this self-supporting coil structure

  • To reduce rung tube diameter, simplifying assembly

  • To facilitate direct drive of the coil at a single rung (for each mode). The equivalent parallel resistance at resonance was significantly above 50 ohms for the 144 rung configuration, permitting the use of capacitive-only matching networks. Later in the development process, we decided not to use direct drive, but the option remains

However, we are not claiming that the particular number of rungs we used is optimal. All the coil geometrical parameters (number of rungs, rung and end ring tube diameters, coil length and diameter) are subject to optimization during design and construction of the next prototype. We may even consider switching to a fundamentally different coil winding design, such a saddle coil. That said, any optimization is not expected to dramatically improve the coil’s B-field. Improvements up to 20% may be possible (slightly more if the coil is made smaller).

Along with this, we employ carefully designed inductive power coupling. The inductive coupling blocks DC and acts as a balun (balanced-unbalanced transformer). This is useful in terms of both circuit design (we avoid having to install a transformer) and safety concerns (no direct path from the AC to the coil). It also allows adjusting the load resistance at resonance. Inductive coupling perturbs the current distribution in the coil significantly less than directly driving an individual rung. As a result, the resonator possesses a superior quality factor of approximately 300 [30]. Therefore, we may achieve any desired electric field levels of up to 50–100 V/m within the lower body due to the resonance effect and still use standard power electronics equipment.

A computational model of a particular resonator constructed in this study is shown in Fig. 5.3a with the electric current distribution to scale. The coil has a diameter of 0.94 m and a length of 1.10 m; the coil resonates at 100 kHz or at 145 kHz depending on the values of the bridging capacitors. The coil consists of two rings (top and bottom) joined via multiple straight rungs, each bridged with a lumped capacitor at its center. The capacitors control the coil’s resonant frequency. The resonating coil is fed via two lumped ports in quadrature, or using inductive coupling with two loops in quadrature as explained below.
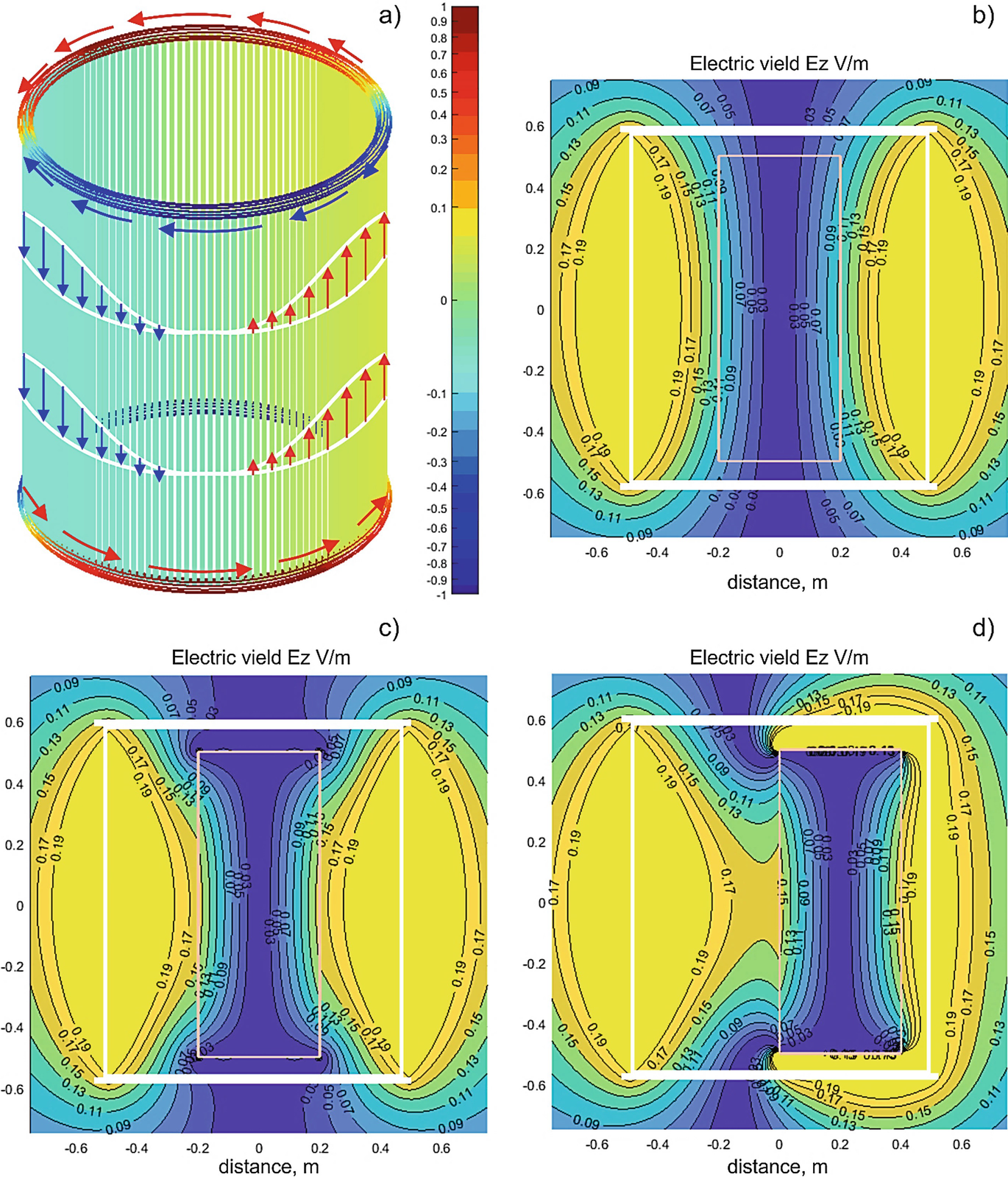
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig3_HTML.png
Fig. 5.3

Current distribution in the coil resonator and the associated solenoidal electric field created by the coil when the ring current amplitude is 1 A for one resonant mode. (a) Electric current distribution in the coil along with the current color bar to scale; (b) Magnitude of the vertical electric field Ez in V/m for an empty coil in the coronal plane; (c) Magnitude of the vertical electric field Ez in V/m for the coil with a coaxial conducting cylinder 0.4 × 1 m inside; (d) Magnitude of the vertical electric field Ez in V/m for the coil with a conducting cylinder 0.4 × 1 m shifted in the transverse plane inside

From the modeling point of view, the resonant electric current in both rings at any fixed time instant behaves like a full period of a sine function of polar angle φ. This ring current distribution is shown in Fig. 5.3a. As time progresses, the ring current distribution shown in Fig. 5.3a rotates with angular frequency ω. As a result, the time-domain ring current i(t, φ) in the top and bottom rings can be expressed in the form

$$ i\left(t,\varphi \right)=\pm {I}_0\cos \left(\omega t-\varphi +\pi /2\right),\kern0.5em \varphi \in 0,2\pi $$
(5.4)
where I0 is the current amplitude determined by the excitation power and by the quality factor (or the “gain”) of the resonator.
The AC current in each rung shown in Fig. 5.3a does not change along its length. Simultaneously, at any fixed time instant, it also varies from rung to rung as a harmonic function of the polar angle φ with the full period corresponding to the ring circumference. This rung current distribution is shown in Fig. 5.3a. As time progresses, the rung current distribution shown in Fig. 5.3a also rotates with angular frequency ω. Each individual time-domain rung current density j(t, φ) can be expressed in the form
$$ j\left(t,\varphi \right)=\frac{I_0}{F}\cos \left(\varphi +\omega t\right),\kern1em F=\frac{1}{2}\sum \limits_{m=0}^{\frac{N}{2}-1}\sin \left(\frac{2\pi m}{N}\right),\kern1em \varphi \in 0,2\pi $$
(5.5)
where N is the total number of rungs. This form obeys the current conservation law, or Kirchhoff’s Current Law (KCL), at every ring-rung junction.

The useful current, which creates a nearly constant horizontal rotating magnetic field Br with amplitude B0 and axial rotating electric field Ez according to Eq. (5.2), is the rung current density j(t, φ). Contributions of each rung add up in a constructive manner. The ring current, on the other hand, does not contribute to the axial (or vertical) electric field, Ez. However, it may create a strong transverse electric field very close to the rings.

It should be pointed out that Eqs. (5.4) and (5.5) describe the rotating current behavior, which is a combination of two elementary resonant modes. Each elementary mode does not rotate and appears as depicted in Fig. 5.3a. However, when excited in quadrature (with a 90 degree phase shift and a 90 degree excitation offset along the coil circumference), both modes combine to create the current distribution given by Eqs. (5.4) and (5.5) and the associated rotating electric field. The rotation phenomenon enables us to treat the entire body and not merely a singular component or region.

5.2.4 Solenoidal Electric Field Distribution with and without a Simple Conducting Object

Figure 5.3b–d shows the resulting electric field distribution in the coil (coronal plane) when the current amplitude I0 = 1 ampere in either ring given by Eq. (5.4). The results are given for one resonant mode, as shown in Fig. 5.3a. Due to linearity, this result can simply be scaled for other excitation levels. Accurate field computations have been performed with the fast multipole method described in [89]. The magnitude of the axial component Ez in V/m for an empty coil is shown in Fig. 5.3b. The electric field is indeed zero at the coil’s center.

When a conducting object representing a load is inserted into the coil, the field distribution changes. Figure 5.3c shows the distribution when a conducting cylinder with a diameter of 0.4 m and a length of 1 m is inserted into the coil along its axis. The particular conductivity value σ does not matter since only the conductivity contrast, (σ − σair)/(σ + σair), is present in the solution [66]. This value is always unity since σair = 0.

An interesting and useful effect is observed in Fig. 5.3c: we see a “pulling” of the electric field into the cylinder close to the coil center. This is due to surface charges that appear at and near the cylinder tips. As a result, the electric field close to the cylinder surface at the center plane of the coil increases by nearly 36%.

Another remarkable observation (this effect is common in MRI RF coils) follows from Fig. 5.3d where the conducting cylinder has been shifted from the coil axis to the right by 0.2 m. While the electric field outside the conducting cylinder clearly changes, the field within the cylinder remains nearly the same, as observed in Fig. 5.3c. This may be explained as a result of the electric field being induced by the magnetic field, similar to eddy currents. Since the magnetic field is relatively homogeneous in the transverse plane of the coil, the induced electric fields in a load should not strongly depend on the transverse position of the load within the coil.

These rudimentary simulations allow us to establish two basic facts relevant for the analysis of realistic electric field distributions in a human body within the coil. First, we expect that the average transcutaneous electric field will be slightly higher than predicted by the air-filled coil model in dorsal, abdominal, and lumbar body regions. Second, we expect that the field within the body will not change significantly when the body is moved within the coil in the transverse plane; this circumstance seems to be useful from a practical point of view.

5.2.5 Contribution of Unpaired Electric Charges

Generally, the total electric field within the coil is expressed in terms of two auxiliary potentials. Instead of Eq. (5.1), one has

$$ E=-\partial A/\partial t-\nabla \varphi $$
(5.6)
where φ is the scalar electric potential and A is the magnetic vector potential. In the quasistatic approximation to Maxwell’s equations, the time derivative in the Lorentz gauge $$ \frac{1}{c^2}\partial \varphi /\partial t+\nabla \cdot A=0 $$ is neglected (which gives us the Coulomb gauge, ∇ · A = 0), while it is still kept in Eq. (5.6). As a result, the − ∇ φ term in Eq. (5.6) becomes a conservative electric field contribution due to charge density alone, while the −∂A/∂t term is a true solenoidal electric field contribution due to current density alone.

In accordance with the (quasi)electrostatic theory [90], the conservative electric field is blocked by charges induced on a surface of a conducting object and does not penetrate into the object. Therefore, its contribution is ignored in the present study, similar to the theoretical models of transcranial magnetic stimulation or TMS. Note that this charge contribution may be quite large in the present problem, close to the bridging capacitors.

We have also performed full-wave ANSYS ED simulations of this coil and found that the capacitor voltage drop E-field does not significantly affect the E-field within the patient. The externally applied conservative E-field is expelled from the patient by the high conductivity of tissues. Only the E-field induced from the B-field is important.

5.2.6 Power Amplifier/Driver

In order to create the rotating magnetic and electric fields, as seen in Figs. 5.2a, b, two resonant modes are excited in the coil resonator. These modes display the same current distribution as shown in Fig. 5.3a, but rotated by 90 degrees about the coil axis with respect to each other as well as having an additional temporal phase shift of 90 degrees.

To accomplish this, a custom designed class-D, high-efficiency, single-frequency power amplifier (PA), whose circuit schematic is presented in Fig. 5.4a, was constructed and prototyped, as shown in Fig. 5.4b, c. The upper block in Fig. 5.4a is a class-S modulator, which is followed by two class-D output stages in quadrature, exciting the two resonant modes. The PA has two outputs, one for each resonant mode, and generates a harmonic power RF signal at a fixed carrier frequency at each output. At present, this frequency is typically around 100 kHz. At the same time, the same PA may be tuned to operate at any carrier frequency from 30 kHz to 300 kHz in the LF band. The PA operation, including variable power levels, an optional variable modulation or tonic frequency, and a semiautomatic patient-specific RF frequency tuning procedure, which is automated via a microcomputer board, can be seen in Figs. 5.4c and 5.5d.
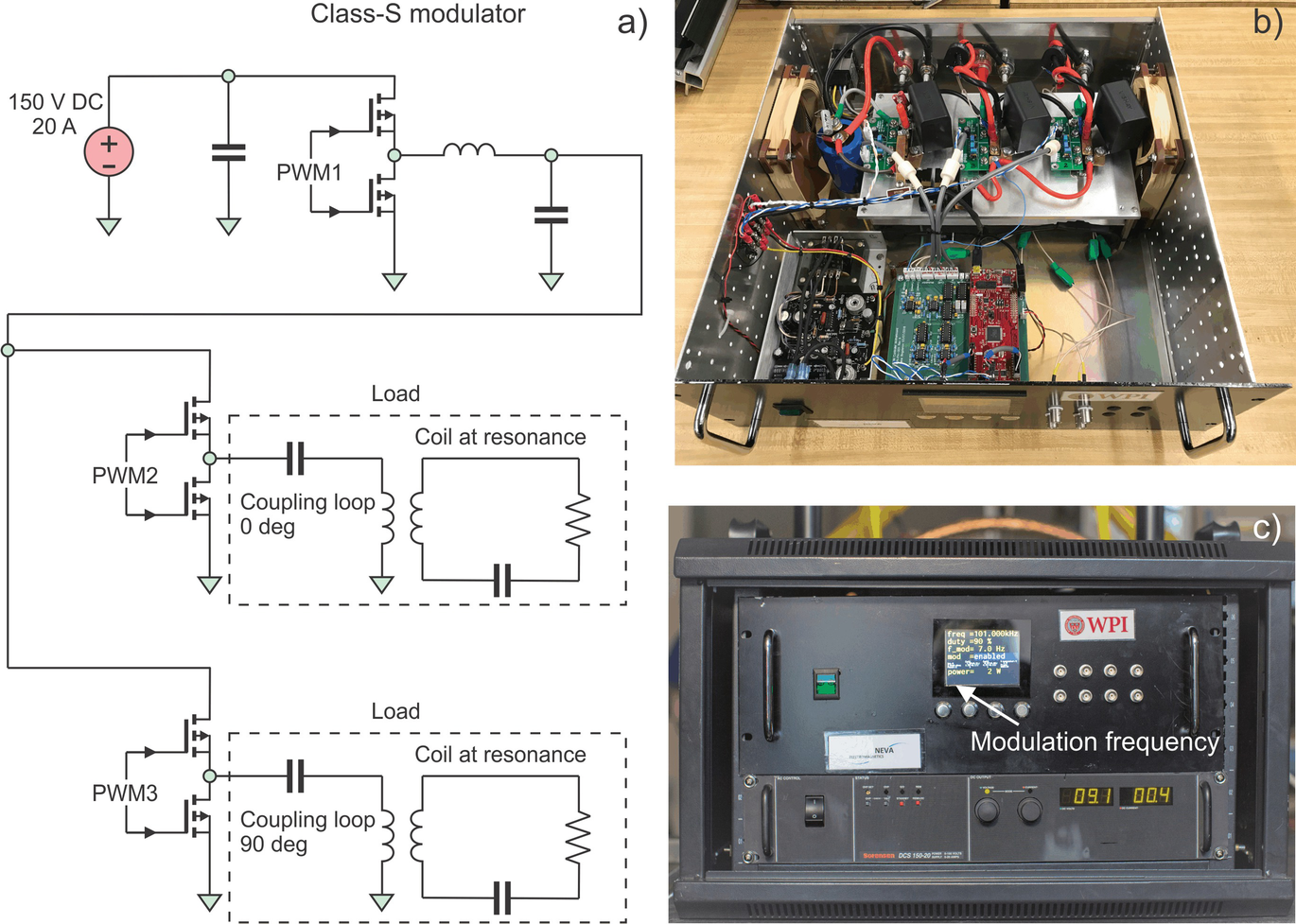
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig4_HTML.png
Fig. 5.4

(a) High-level circuit schematic of the two-channel power amplifier. (b) Rackmount air-cooled assembly of the electronic hardware. (c) Amplifier display controlling output power and modulation frequency (if used)

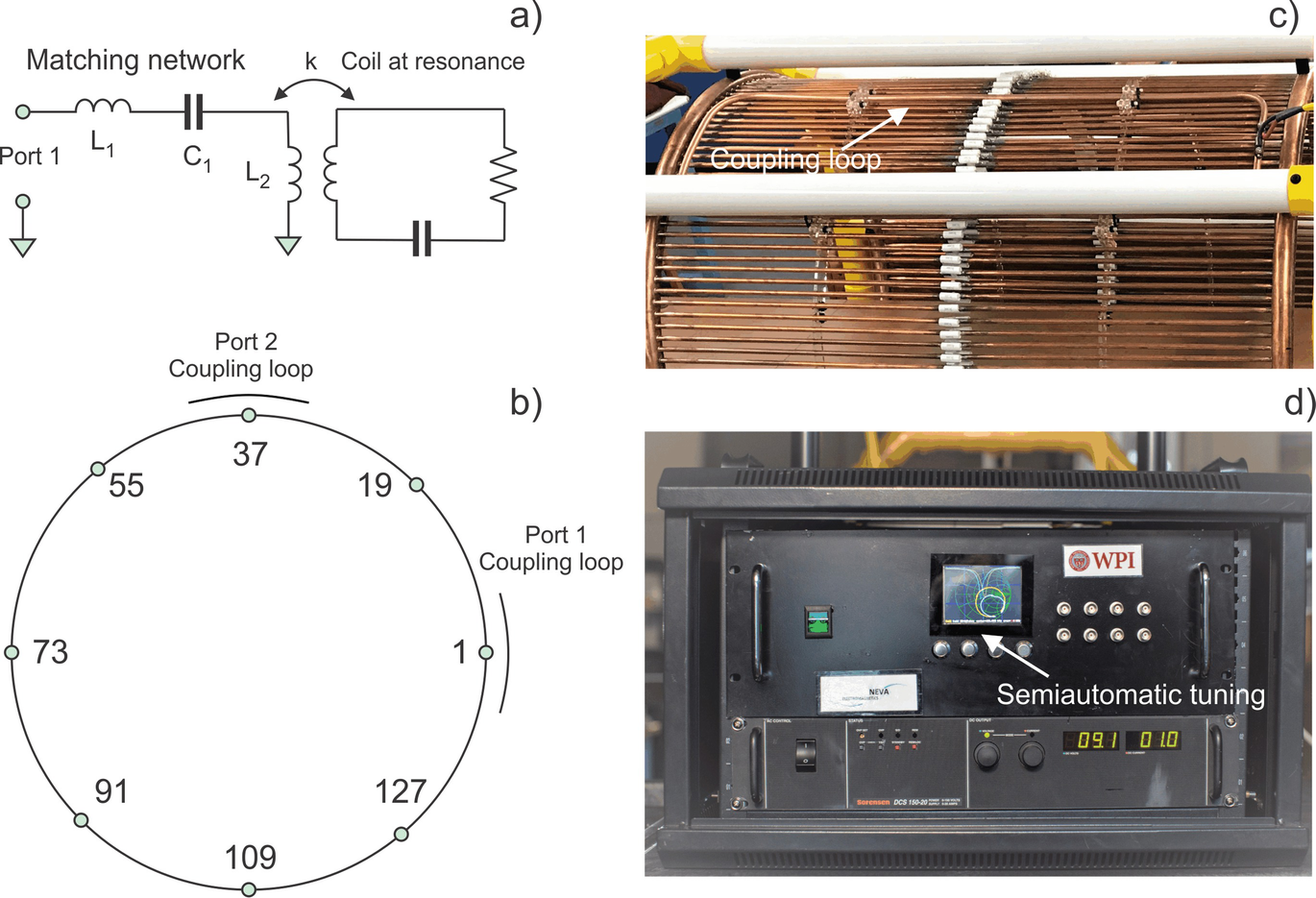
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig5_HTML.png
Fig. 5.5

(a) Matching and tuning network of the power amplifier. (b) Assembly of two coupling-loop feed around the coil circumference with 144 rungs. (c) Noncontact inductive coupling of the power amplifier to the coil resonator at one port. (d) Smith chart/reflection coefficient display of the power amplifier controller used for semiautomatic tuning at any desired time instant

The PA output stage is powered by a 3 kW Sorensen DCS 150–20 Variable Regulated DC (direct current) power supply seen at the bottom of Fig. 5.4c. When connected to a standard three-phase 208 VAC outlet, the max RF output power is about 2.9 kW, based on 3 kW DC power. Alternatively, when connected into a single-phase 240 VAC outlet, the max RF power reduces to about 2.3 kW based on 2.4 kW DC power.

Arbitrary modulation (pulse or CW) of the carrier signal with a maximum modulation frequency component of 1 kHz is available via the modulator. The modulation bandwidth is limited mainly by the coil envelope time constant of about 1 ms. Typical modulation is sinusoidal in the 0.5–100 Hz range, generated by the PA firmware.

The PA also monitors its output power and load impedance. It uses this information to automatically adjust the carrier frequency in a narrow band such that the output power remains on target. The amplifier cost, including the DC power supply, is under $10,000. The prototype 100 kHz PA was assembled in a rackmount case shown in Figs. 5.4b, c.

The reason for designing a custom, fixed-frequency PA is the lack of an affordable and appropriate commercial model. Industrial low-frequency RF power supplies, e.g., Comdel’s CLB3000, are costly and require a matched 50 Ω load. Because our load impedance varies widely with frequency, keeping the load matched is a challenge. It would require load impedance monitoring and fine frequency control (potentially difficult with a commercial unit), and/or a software-controlled matching network (costly). Additionally, generating two outputs in quadrature would require either a 90° hybrid (another costly component), or phase-locking two commercial PAs at a 90° phase difference, which can be difficult. Finally, the majority of commercial PAs require water cooling, whereas our PA relies on air cooling. One disadvantage of our custom design is its unknown reliability, a factor that will be proven over time.

5.2.7 Coupling and Matching the Power Amplifier to the Resonating Coil

The amplifier is coupled to the resonating coil inductively via two proximate loops. One such loop is shown in Fig. 5.5c. Apart from certain technical advantages of the inductive coupling, this methodology assures that there is no direct current path from the AC power outlet to the coil. This design enhances overall device safety at any power level, including high-power operation.

The matching network for a single coil port is shown in Fig. 5.5a. Two ports with identical matching networks are located 90° apart around the coil structure, as shown in Fig. 5.5b. The port matching network consists of a series capacitance C1, series inductance L1, and the fixed inductance L2 of the inductive loop seen in Fig. 5.5c.

The matching network is tuned such that the load looks mostly resistive over a small frequency band around the coil’s resonance. For example, the load reactance stays quite low from 99.85 kHz to 100.15 kHz, while the resistance varies from 1.3 Ω to 6 Ω. Because the coil resonance shifts as the coil heats up, the operating frequency must be actively adjusted to compensate for this change, or the output power will vary.

We used two Cornell Dubilier Electronics 940C20S47K-F per rung (C = 0.094 μF per rung). These are 0.047 μF, 2 kV DC, 500 V AC-rated polypropylene film capacitors. They have a typical ESR of 12 mΩ at 100 kHz (Q = 2800), and a max RMS current rating of 5.2 A at 70 °C. We exceed this current rating by about 50% at full power. However, we have measured capacitor temperatures using an IR camera. They are below 70 °C, well within the operating range.

Another important safety feature of the matching network is its benign power envelope step response. The matching network avoids large spikes in PA output current while energy is building up in the resonating coil.

Finally, the matching network presents a sufficiently inductive impedance to higher harmonics of the PA output voltage. This protects the output stage, and ensures that voltage transitions occur when the output current is low, thereby improving efficiency. The efficiency of the PA with the expected load is estimated to be greater than 90% over a wide output power range.

5.2.8 Tuning Procedure

The primary adjustable components are the series capacitance C1 in Fig. 5.5a and the coil rung capacitors at the numbered locations in Fig. 5.5b. First, the coil needs to be manually tuned by installing smaller capacitors in parallel with the primary coil capacitors at strategic locations. Coil adjustments include mode decoupling, tuning of each mode to the same frequency, and impedance matching for each mode (at the coupling loop). Since capacitance is normally only added, the coil only tunes down in frequency.

The semiautomatic tuning procedure implies adjusting PA frequency in a very narrow frequency range. It ensures that the reflection coefficient of both modes stays below −25 dB when matched to the maximum-power coil impedance of Z0 = 2.5 Ω and that both resonances are within a 20 Hz band. The tuning procedure is controlled and guided by the Smith chart/reflection coefficient display of the PA controller seen in Fig. 5.5d. It includes a number of well-defined steps, and is applied to the coil at its designated operating location in an effort to account for the presence of large nearby metal objects. The tuning procedure is simple to perform.

5.2.9 Coil Assembly, Device Setup, and Operation

A resonator coil prototype made of thin-walled, light copper tubing was constructed; it is shown in Figs. 5.6a, b and 5.7. Tubing thickness was kept at ¾ mm or greater to avoid excessive eddy current losses in the copper. The capacitor size in Fig. 5.6a is relatively large since those components must operate at significant currents levels, up to 18 A RMS per rung for a maximum power of 3 kW, and at large voltages, up to 300 V RMS across the capacitor. The total coil weight without the frame is approximately 120 lbs. (54 kg).
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig6_HTML.jpg
Fig. 5.6

(a) Complete framed resonator coil unit with the PA. (b) Smith chart/reflection coefficient display of the power amplifier controller to be used for semiautomatic tuning for an individual subject/patient. (c) Amplifier display controlling output power and modulation frequency for harmonic modulation

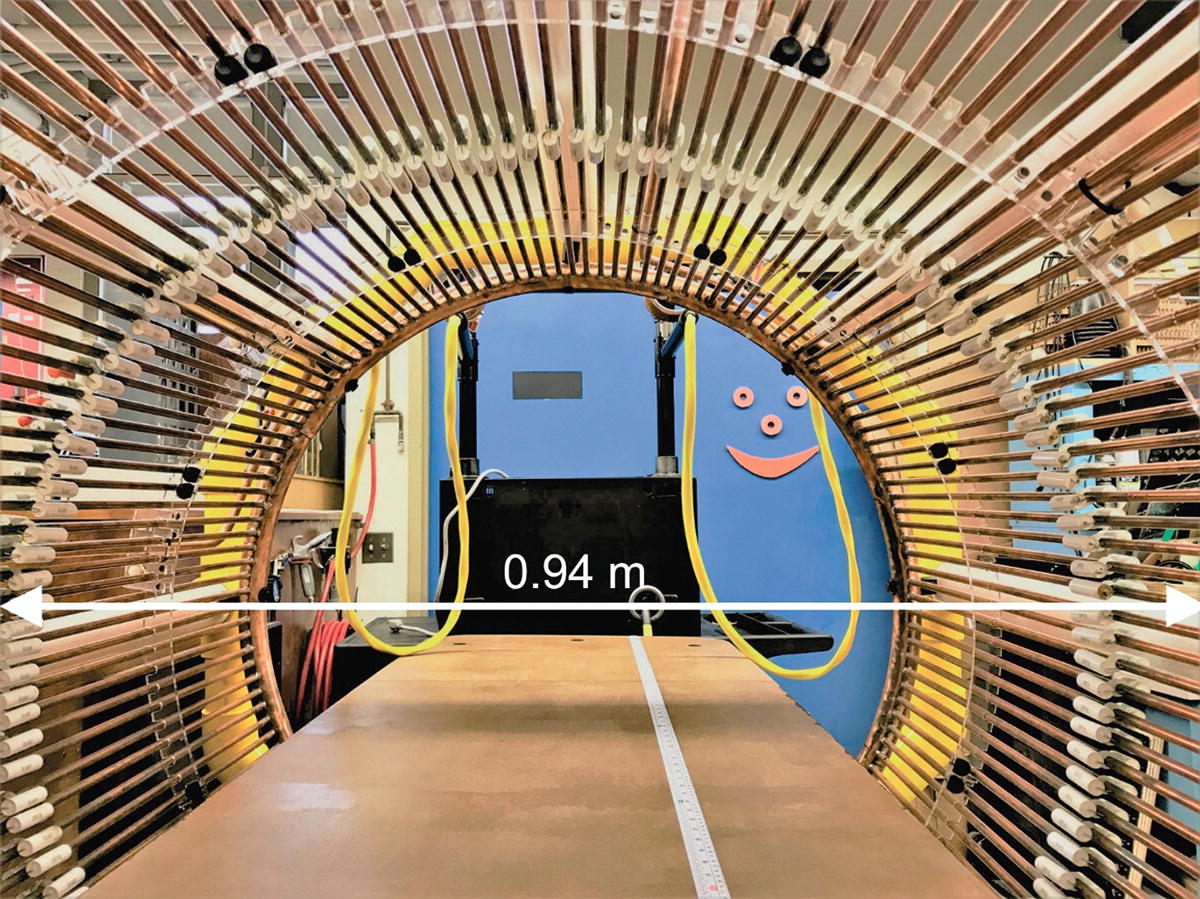
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig7_HTML.jpg
Fig. 5.7

Active area of the subthreshold resonator device

This durable coil prototype was then framed, augmented with a horizontal bed, and placed horizontally to enable a subject to rest in the coil, as shown in Fig. 5.6a, which simultaneously shows the complete device setup. The entire coil frame is portable. The distance between the PA, which is connected to the inductive coupling loops of the coil via two isolated cables, can vary from 1 to 3 m, although larger distances may be possible. As mentioned above, there is no direct ohmic current path from the AC power outlet to the coil, which is an important safety feature.

An operator sets the power level, the modulation frequency, and performs RF tuning at the beginning of the resonator operation and for a particular coil load. At the maximum power level, the ring conductors of the coil heat up to approximately 70–75 °C at continuous operation, as illustrated in Fig. 5.8. Continuous coil operation at the maximum input power of 3 kW was tested multiple times with an uninterrupted operation time of up to 2 h and with a cumulative operating time in excess of 100 h.
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig8_HTML.jpg
Fig. 5.8

Infrared map of the coil and PA(rear) temperature distribution after 30 min of operation at maximum power obtained with FLIR A325sc IR camera

5.2.10 Quality Factor of the Resonator and the Magnetic Field Strength

The achievable field strength in the coil is determined by three factors: the strength of the PA, the quality factor Q or the “gain” of the resonator, and the coil volume. When the quality factor is high, large field values within the coil can be achieved at a modest input power.

When measured across one of its rung capacitors, the birdcage coil behaves like a parallel resonator in a narrow frequency range around the resonant mode. Using a setup with a signal generator and oscilloscope, the resonator’s quality factor has been estimated in the form:

$$ Q=\frac{f_0}{\left({f}_{\mathrm{U}}-{f}_{\mathrm{L}}\right)\left(1-\frac{V_1}{V_0}\right)} $$
(5.7)
where f0 is the resonance frequency and voltage V0 is the open-circuited generator voltage. Derivation of Eq. (5.7) is given in Appendix A. Voltage V1 is measured at resonance (where it is maximized). fL and fU are the lower and upper frequencies, respectively, where voltage V1 drops by 3 dB from its peak at resonance. This method is accurate in the high Q limit. The experimental data for 100 kHz and 145 kHz are given in Table 5.1. Table 5.1 reports a Q-factor value of about 300 and a minimum difference between loaded (with a human body) and unloaded coil, which is to be expected at this low frequency. These values agree with the theoretical/simulation predictions to within 10%. With decreasing frequency, the Q-factor will decrease approximately proportional to the square root of the resonant frequency.
Table 5.1

Measured Q-factors for the coil resonator at 100 kHz and 145 kHz, respectively

Coil

f0, kHz

fL, kHz

fU, kHz

Q

Unloaded

145.30

144.567

145.875

295.8

Loaded

145.28

144.566

145.879

292.2

Unloaded

101.42

101.008

101.827

277.3

Loaded

101.43

101.009

101.835

275.0

The load is a 200 lb. subject

The established quality factor values are superior to the values reported in the literature for known low-frequency resonator coils (used for low-field MRI) in Table 5.2. Note that all listed competitors have a much smaller coil size/volume and typically a lower quality factor.
Table 5.2

Characteristics of existing low-frequency RF coils given for comparison with the present resonator prototype

Ref.#

Type of the coil

Frequency, kHz

Q (unloaded)

[83]

Wound birdcage coil (84 mm long and has a diameter of 73 mm)

386

180

[84]

Wound birdcage coils and a solenoid. The diameter and the length of the coils are 70 mm

238/425

100–280

[85]

27 tTurn saddle coil made of Litz wire with 8 cm diameter

373

105

[86]

4-Coil Whiting-Lee configuration, 33 cm long

83.6

100

[87]

Solenoidal coils; 6–46 cm in length and 4–52 cm in diameter

210/275

60–30, reduced Q

[88]

Cylindrical saddle-shaped loops (5 saddle pairs of 10 turns each), coil diameter is 26 mm

87

NA

It is important to point out again that the quality factor in Table 5.1 is weakly affected by body loading, in contrast to conventional high-frequency MRI RF coils. This observation, also mentioned in Ref. [84] and other sources, is a limitation of the present electromagnetic stimulator. The RF power losses are mostly in the coil itself, and not in the human body.

B-field measurements have been performed via a calibrated single-axis coil probe located at the coil axis. The B-field magnitude was 1.01 mT at the coil center and at full power (3 kW DC) at 100 kHz. The measured and theoretical results differ by no more than 10%. At the full input power level of 3 kW, the amplitude of the resonant ring current I0 at 100 kHz in two coil rings reaches 603 A, while the amplitude of the rung current reaches 26 A.

5.3 Device Safety Estimates

5.3.1 Peripheral Nervous System (PNS) Stimulation Threshold

The present low-frequency subthreshold electrostimulation device must not exceed the PNS simulation threshold to operate safely and without unpleasant sensation. Guidelines from the International Commission on Non-Ionizing Radiation Protection (Table 5.2 of [91]) require the occupational exposure to an electric field to be limited to a value of approximately 27 V/m RMS at 100 kHz and by a value of 39 V/m RMS at 145 kHz (the so-called basic restrictions [91]). These restrictions are mainly due to limits on peripheral nerve stimulation [91] and should therefore be respected. Other relevant results on the PNS stimulation thresholds at lower frequencies are presented in Refs. [92–94].

5.3.2 Specific Absorption Rate (SAR)

Safety estimates also rely upon the levels of the specific absorption rate (SAR) within the body. The SAR is the energy absorption rate that causes body temperature to rise due to an imposed electromagnetic field. The maximum value of SAR1g in the body must be below 10 W/kg required by the FDA-accepted safety standard [95, 96]. The global-body SAR must be below the 2 W/kg limit [95, 96].

5.3.3 Method of Analysis

SAR and electric field measurements cannot be performed easily for human subjects in vivo. SAR and device performance estimates are typically derived and accepted today from computational electromagnetics (CEM) simulations performed with detailed virtual humans [97]. In this study, we use the multi-tissue CEM phantom VHP-Female v. 5.0 (female/60 year/162 cm/88 kg, obese) [97–103] derived from the cryosection dataset archived within the Visible Human Project® of the US National Library of Medicine [104]. The phantom includes about 250 individual tissues and is augmented with material property values from the IT’IS database [105]. The average-body conductivity is assigned as 0.25 S/m, which reflects a mixture of muscle and fat.

The primary CEM software used in this study is the accurate commercial FEM solver ANSYS® Electromagnetic Suite 18.2.0 with rigorous adaptive mesh refinement. In addition, and for verification/validation purposes, we employ an in-house boundary element fast multipole method (BEM-FMM) described in Ref. [89]. In the latter case, a higher near-surface resolution can be achieved and the original surface phantom model can be refined and smoothed from approximately 0.5 M triangles to 3.5 M triangles. In this particular study, the human model is placed in the coil at the shoulder landmark, as shown in Fig. 5.9, so that the top of the shoulder coincides with the ring plane. Other configurations have also been considered.
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig9_HTML.png
Fig. 5.9

Multi-tissue CEM phantom VHP-Female v. 5.0 within the resonant coil (ANSYS 18.2.0)

Results obtained with both software packages differ by no more than 2% in the unloaded coil (field at the coil center) and by no more than 25–50% in the coil loaded with the multi-tissue human body. The latter deviation may be explained by somewhat different surface meshes.

Below we report simulations at two power levels: 1.5 kW input power and 3 kW input power. The first power level is the half power level of the amplifier driver; the second power level corresponds to full power. At full power level, the amplitude of the resonant ring current I0 in Eqs. (5.4 and 5.5) reaches 603 A, while the amplitude of the rung current reaches 26 A.

5.3.4 Electric Field Levels

Figure 5.10 shows the simulated RMS levels of the electric field in the body at 100 kHz and at the input power level of 1.5 kW obtained via the BEM-FMM simulations. We observe that, at half power level of the amplifier driver, the fields everywhere in the body do not generally exceed 30 V/m RMS and are thus within the ICNIRP guidelines. As expected, higher field levels are observed closer to the surface; the field gradually decreases toward the center of the body.
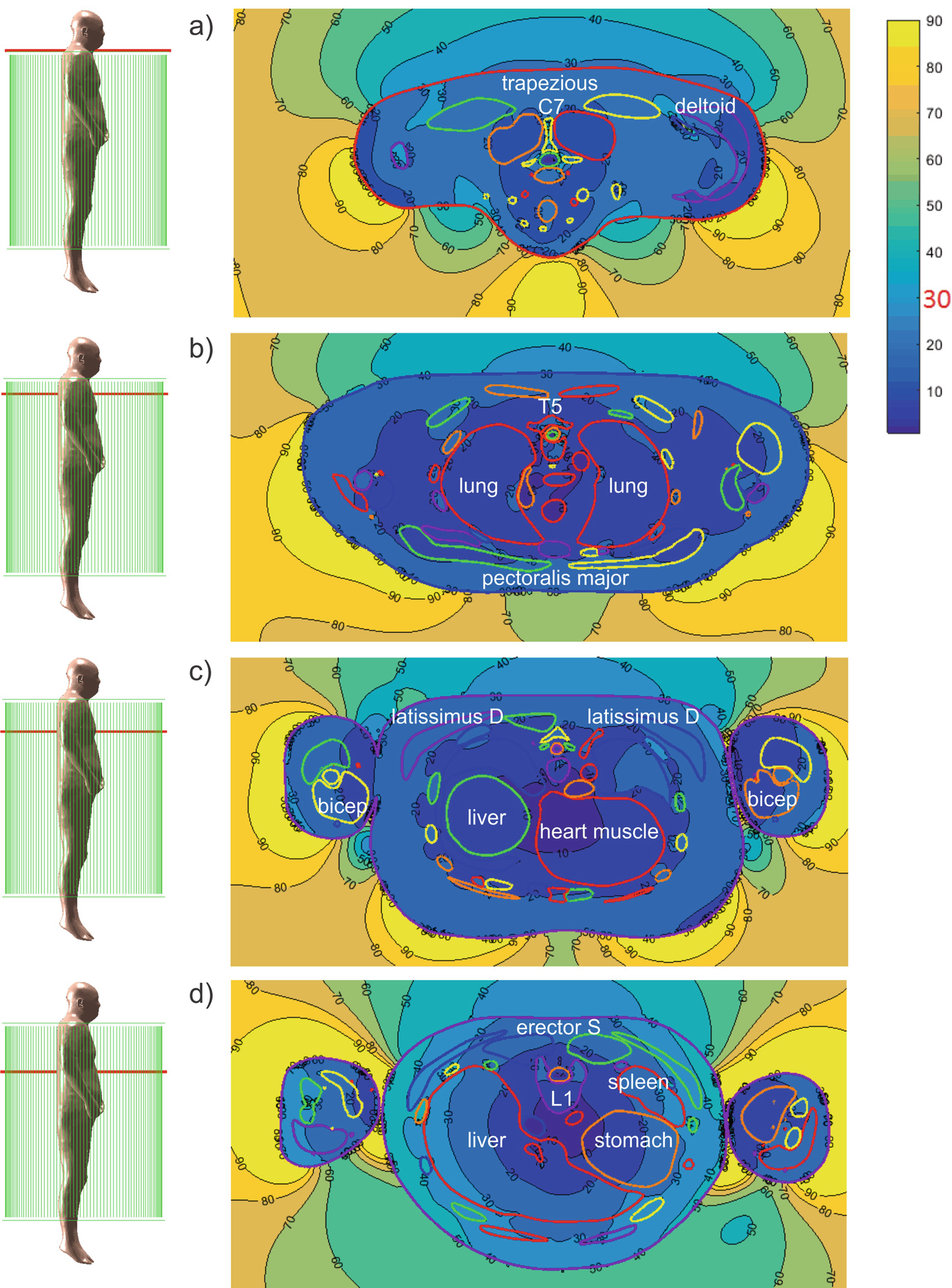
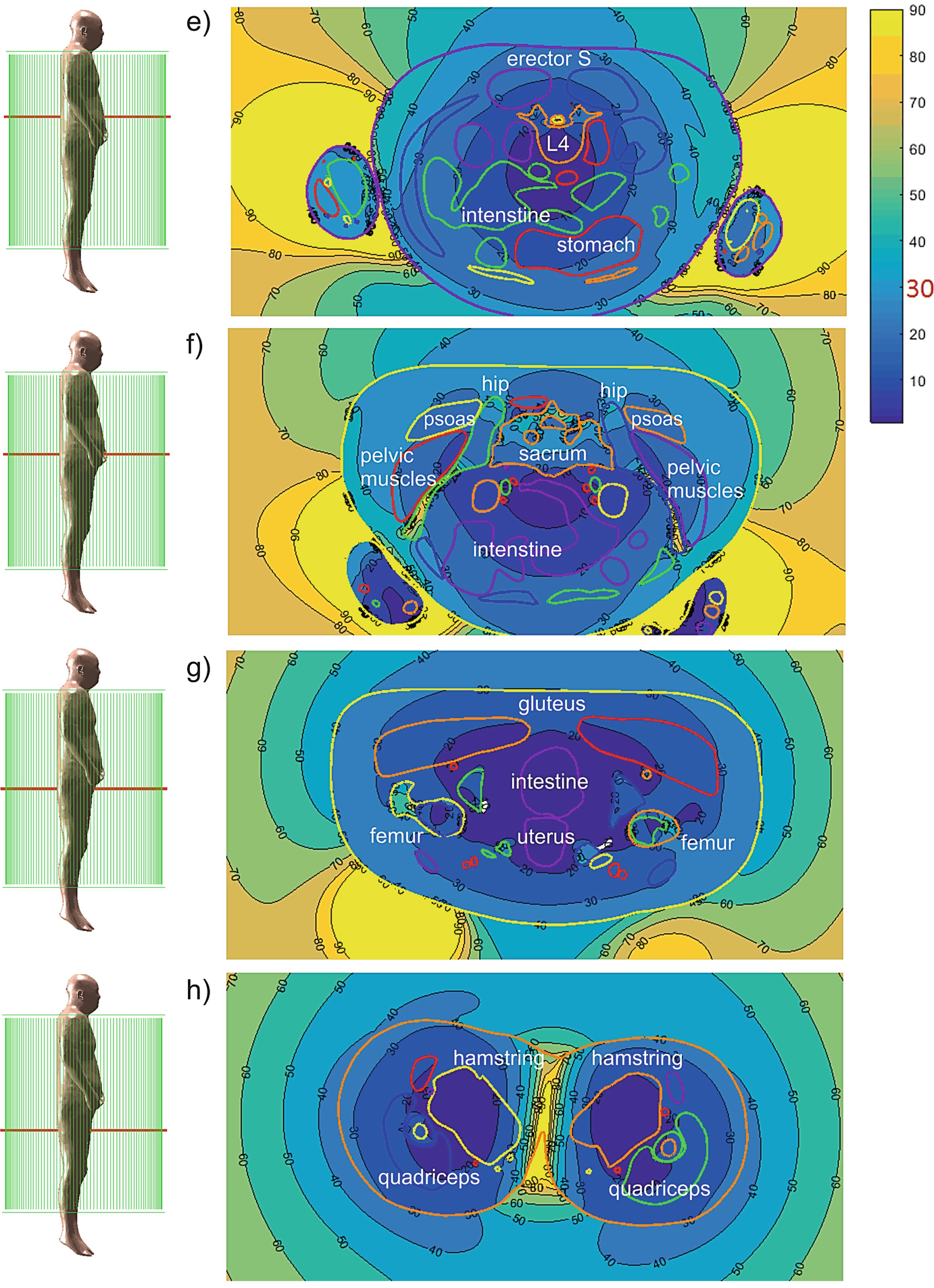
../images/473436_1_En_5_Chapter/473436_1_En_5_Fig10a_HTML.png../images/473436_1_En_5_Chapter/473436_1_En_5_Fig10b_HTML.png
Fig. 5.10

Complex RMS magnitude of the electric field (V/m) at 1500 W input power

Quantitative estimates of the average electric field for every particular tissue obtained via ANSYS Electromagnetic Suite 18.2.0 are given in Table. 5.3. Note the lower electric fields in the intracranial volume. Additionally, we observe higher electric fields in the individual body muscles. It is also interesting to observe that the fields in bone may be quite high, in particular in the femur and pelvic bones.
Table 5.3

Computed electric field levels (V/m RMS) in every individual tissue at 1.5 kW input power (ANSYS® Electromagnetic Suite 18.2.0)

Mesh

Tissue

Avg. E field (V/m RMS)

Mesh

Tissue

Avg. E field (V/m RMS)

1

Air Internal Maxillary Sinus Left

7.7

39

Cuneiform Medial right

0.6

2

Air Internal Maxillary Sinus Right

6.9

40

discC02C03

10.3

3

Arteries

10.5

41

discC03C04

11.6

4

Bladder

28.0

42

discC04C05

14.3

5

C01

14.5

43

discC05C06

16.9

6

C02

13.6

44

discC06C07

19.0

7

C03

14.8

45

discC07T01

20.6

8

C04

18.5

46

discL01L02

13.9

9

C05

21.7

47

discL02L03

11.5

10

C06

26.1

48

discL03L04

8.4

11

C07

29.6

49

discL04L05

4.7

12

Calcaneous left

0.6

50

discL05L06

7.1

13

Calcaneous right

1.1

51

discL06S00

13.8

14

Cartilage1 Left

18.5

52

discT01T02

20.2

15

Cartilage1 Right

19.9

53

discT02T03

17.6

16

Cartilage2 Left

19.7

54

discT03T04

17.9

17

Cartilage2 Right

20.3

55

discT04T05

17.4

18

Cartilage3 Left

21.2

56

discT05T06

15.8

19

Cartilage3 Right

20.9

57

discT06T07

15.2

20

Cartilage4 Left

22.5

58

discT07T08

14.4

21

Cartilage4 Right

21.8

59

discT08T09

13.6

22

Cartilage5 Left

24.3

60

discT09T10

13.2

23

Cartilage5 Right

22.6

61

discT10T11

12.5

24

Cartilage6 Left

36.3

62

discT11T12

13.2

25

Cartilage6 Right

35.9

63

discT12L01

13.4

26

Cerebellum

1.4

64

Eye Left

5.0

27

Clavicle left

55.6

65

Eye Right

5.3

28

Clavicle right

34.9

66

Feet1Phalange left

0.5

29

Coccyx

42.6

67

Feet1Phalange right

0.4

30

CSF OuterShell

3.5

68

Feet2Phalange left

0.4

31

CSF Ventricles

0.4

69

Feet2Phalange right

0.4

32

Cuboid Left

0.9

70

Feet3Phalange left

0.3

33

Cuboid Right

0.6

71

Feet3Phalange right

0.4

34

Cuneiform Intermediate left

1.3

72

Feet4Phalange left

0.4

35

Cuneiform Intermediate right

0.5

73

Feet4Phalange right

0.6

36

Cuneiform Lateral left

1.1

74

Feet5Phalange left

0.4

37

Cuneiform Lateral right

0.4

75

Feet5Phalange right

0.7

38

Cuneiform Medial left

1.3

76

Femur Bone Marrow Left

7.1

77

Femur Bone Marrow Right

8.6

117

Humerus right

23.1

78

Femur left

69.3

118

Intestine

20.6

79

Femur right

83.7

119

Jaw lower

10.0

80

Fibula left

5.9

120

Kidney left

29.3

81

Fibula right

5.4

121

Kidney right

27.2

82

Gray Matter Spinal Cord

1.5

122

L01

27.9

83

Hands1 1Phalange left

10.2

123

L02

25.3

84

Hands1 1Phalange right

9.5

124

L03

22.1

85

Hands1 2Phalange left

9.5

125

L04

19.0

86

Hands1 2Phalange right

12.1

126

L05

14.4

87

Hands1 3Phalange left

12.2

127

L06

17.9

88

Hands1 3Phalange right

13.4

128

Liver

29.8

89

Hands2 1Phalange left

7.6

129

Lungs

19.4

90

Hands2 1Phalange right

7.1

130

Median Nerve left

11.6

91

Hands2 2Phalange left

8.1

131

Median Nerve right

13.0

92

Hands2 2Phalange right

8.5

132

Muscle Bicep left

11.9

93

Hands2 3Phalange left

7.1

133

Muscle Bicep right

12.9

94

Hands2 3Phalange right

9.5

134

Muscle Calf left

5.0

95

Hands3 1Phalange left

6.4

135

Muscle Calf right

5.2

96

Hands3 1Phalange right

6.2

136

Muscle Deltoid left

18.7

97

Hands3 2Phalange left

8.1

137

Muscle Deltoid right

19.3

98

Hands3 2Phalange right

8.6

138

Muscle Erector spinae left

26.8

99

Hands3 3Phalange left

9.3

139

Muscle Erector spinae right

26.9

100

Hands3 3Phalange right

11.0

140

Muscle Forearm Extensors left

6.9

101

Hands4 1Phalange left

7.2

141

Muscle Forearm Extensors right

8.6

102

Hands4 1Phalange right

6.9

142

Muscle Forearm Flexors left

6.9

103

Hands4 2Phalange left

10.4

143

Muscle Forearm Flexors right

7.2

104

Hands4 2Phalange right

10.0

144

Muscle Gluteus left

27.9

105

Hands4 3Phalange left

11.1

145

Muscle Gluteus right

27.2

106

Hands4 3Phalange right

10.7

146

Muscle Hamstring left

18.9

107

Hands5 1Phalange left

9.0

147

Muscle Hamstring right

19.1

108

Hands5 1Phalange right

10.3

148

Muscle Latissimus Dorsi left

36.6

109

Hands5 2Phalange left

11.0

149

Muscle Latissimus Dorsi right

38.5

110

Hands5 2Phalange right

12.6

150

Muscle Neck Combined left

13.6

111

Hands5 3Phalange left

10.3

151

Muscle Neck Combined right

13.4

112

Hands5 3Phalange right

12.1

152

Muscle Obliques left

39.5

113

Heart Muscle

14.2

153

Muscle Obliques right

40.1

114

Hip left

60.0

154

Muscle Pectoralis major left

21.7

115

Hip right

61.4

155

Muscle Pectoralis major right

20.9

116

Humerus left

20.7

156

Muscle Pectoralis minor left

19.2

157

Muscle Pectoralis minor right

18.6

194

Ribs left8

47.3

158

Muscle Pelvic Combined left

25.7

195

Ribs left9

46.1

159

Muscle Pelvic Combined right

25.0

196

Ribs left10

48.5

160

Muscle Psoas left

13.9

197

Ribs left11

51.7

161

Muscle Psoas right

13.9

198

Ribs left12

39.0

162

Muscle Quadriceps left

20.2

199

Ribs right1

29.6

163

Muscle Quadriceps right

19.9

200

Ribs right2

26.2

164

Muscle Rectus Abdominis left bottom

32.3

201

Ribs right3

25.2

165

Muscle Rectus Abdominis left middle

34.9

202

Ribs right4

26.1

166

Muscle Rectus Abdominis left top

39.1

203

Ribs right5

27.2

167

Muscle Rectus Abdominis right bottom

32.5

204

Ribs right6

29.9

168

Muscle Rectus Abdominis right middle

35.4

205

Ribs right7

35.6

169

Muscle Rectus Abdominis right top

38.1

206

Ribs right8

43.2

170

Muscle Sartorius left

18.6

207

Ribs right9

53.9

171

Muscle Sartorius right

17.5

208

Ribs right10

58.9

172

Muscle Tibialis Anterior left

6.2

209

Ribs right11

56.9

173

Muscle Tibialis Anterior right

5.8

210

Ribs right12

40.9

174

Muscle Trapezius left

23.6

211

Sacrum

45.7

175

Muscle Trapezius right

24.0

212

Scapula left

38.2

176

Muscle Tricep left

12.0

213

Scapula right

38.8

177

Muscle Tricep right

14.0

214

Skin Shell

27.8

178

Navicular left

1.8

215

Skull

22.8

179

Navicular right

0.7

216

Sphenoid

8.9

180

Patella left

24.3

217

Spleen

33.9

181

Patella right

22.6

218

Sternum

25.2

182

Peripheral Nerve left

17.1

219

Stomach

22.6

183

Peripheral Nerve Right

14.1

220

T01

28.4

184

Pubic Symphysis

32.1

221

T02

27.2

185

Radial Nerve left

14.6

222

T03

27.2

186

Radial Nerve right

12.4

223

T04

26.9

187

Ribs left1

26.4

224

T05

25.7

188

Ribs left2

30.1

225

T06

25.5

189

Ribs left3

26.4

226

T07

26.2

190

Ribs left4

26.7

227

T08

26.4

191

Ribs left5

28.3

228

T09

26.9

192

Ribs left6

31.5

229

T10

26.1

193

Ribs left7

37.3

230

T11

26.4

231

T12

27.5

240

Trabecular upper right

0.9

232

Talus left

1.3

241

Trachea Sinus

12.4

233

Talus right

0.6

242

Ulna Radius left

8.1

234

Tibia left

8.3

243

Ulna Radius right

7.8

235

Tibia right

7.9

244

Uterus

17.3

236

Tongue

5.2

245

Veins lower

12.5

237

Trabecular lower left

0.5

246

Veins upper

12.4

238

Trabecular lower right

0.8

247

White Matter

1.0

239

Trabecular upper left

0.7

However, the computed local electric fields may considerably exceed the values reported in Table 5.3, in particular by 1.5–6 times. These peak values are less accurate. One potential source of the numerical error is insufficient resolution of lengthy and time-consuming full-body computations very close to the interfaces where higher fields are usually observed.

5.3.5 SAR Levels

The body-averaged or whole-body (global-body) SARbody is given by averaging the local SAR over the entire body volume. In terms of the complex field phasor E(r), one has
$$ SA{R}_{\mathrm{body}}=\frac{1}{V_{\mathrm{body}}}{\int}_{V_{\mathrm{body}}}\frac{\sigma (r)}{2\rho (r)}\kern0.5em E(r)\cdot E{(r)}^{\ast } dV $$
(5.8)
Here, σ(r) is the local tissue conductivity and ρ(r) is the local mass density. At full power of 3 kW and positioned at the shoulder landmark, the global-body SAR computed via ANSYS Electromagnetic Suite 18.2.0 is 0.25 W/kg. Thus, the total power dissipation in the body does not exceed 30 W, i.e., 1% of the total power. The same percentage ratio is valid at half input power.

The second critical estimate is SAR1g, which is given by averaging over a contiguous volume with the weight of 1 g,

$$ SA{R}_{1g}(r)=\frac{1}{V_{1g}}{\int}_{V_{1g}}\frac{\sigma (r)}{2\rho (r)}\kern0.5em E(r)\cdot E{(r)}^{\ast } dV $$
(5.9)
The maximum value of SAR1g in the body computed via ANSYS Electromagnetic Suite 18.2.0 at the full power of 3 kW and located at the shoulder landmark is 4.55 W/kg.

Although this last value might appear to be relatively high, it is still within the corresponding SAR limits in MRI machines [95, 96]. In particular, the major applicable MRI safety standard, issued by the International Electrotechnical Commission (IEC) and also accepted by the U.S. Food and Drug Administration, in the normal mode (mode of operation that causes no physiological stress to patients) limits global-body SAR to 2 W/kg, global-head SAR to 3.2 W/kg, local head and torso SAR to 10 W/kg, and local extremity SAR to 20 W/kg [96]. The global SAR limits are intended to ensure a body core temperature of 39 °C or less [95, 96].

5.4 Discussion

5.4.1 Efficacy of Stimulation

The present study establishes safety and potential feasibility of the resonant neurostimulation device. However, its efficacy for treatment of chronic back pain remains largely unknown. Only clinical trials, which would ideally thoroughly investigate both short-term and cumulative effects of the suggested lower-body electromagnetic treatment, could probably answer this question. Our aim is to provide a doctor with the possibility to vary power, resonant frequency, tonic frequency, and electromagnetic pulse envelope to enable the best possible outcome during the anticipated clinical trial.

5.4.2 Integrated Effect of Stimulation

The present subthreshold stimulation device will not only affect the PNS of the lower back but also muscles, bones, tendons, and cartilage. Evidence suggests that subthreshold pulsed electromagnetic fields may stimulate osteogenesis in vitro and in vivo [106, 107], improve bone quality in osteoporotic and nonosteoporotic cell-based studies [108, 109], human studies [110–114], animal studies [115–121], and augment bone fracture healing [107, 122–124]. Further evidence suggests that TENS therapy stimulates a change in the biochemical and physiological muscle conditions that may lead to muscle relaxation [125, 126]. Some evidence also suggests that the kHz stimulation of the lower body will increase the vascular endothelial growth factor receptor on circulating hematopoietic stem cells [81], whose local niche (the bone marrow of the pelvis, femur, and sternum [127]) might be well affected by the present stimulation device.

Another extremely interesting effect of the kHz peripheral nerve stimulation observed previously in [65, 80] and implicitly in the present device is a potential for sleep improvement. It is not clear how to describe and account these integrated effects of the stimulation. We will attempt to carefully document and report prior relevant literature findings and the corresponding stimulation conditions for nerve/muscle/bone/marrow, and link them to the present stimulation conditions.

5.4.3 Operation as an EMAT

The present electrostimulation device may also operate as an electromagnetic acoustic transducer (EMAT) when a DC current is injected into the tissue via surface electrodes at a specified location. The Lorentz force will excite an ultrasonic field whose frequency is the resonant frequency.

5.4.4 Variation of Resonant Frequency

While fine tuning with a low-loss ferromagnetic load is straightforward, it is quite challenging, however, to vary the resonant frequency of a power resonator, which is usually cast in stone, allowing only a narrow tuning range. In order to do this, we have studied three different methods: a bank of electronically controlled switched power capacitors, a bank of fixed capacitors with low-resistance power relay switches, and a mechanically replaceable bolted joints-based fixed-capacitor bank. Such banks need be constructed for each of the 144 rungs of the coil in Fig. 5.6 or Fig. 5.7 in order to vary the resonant or carrier frequency over the band of, say, 10–100 kHz.

Although the first two approaches are fast and elegant, they are unfeasible. The key is the equivalent series resistance (ESR) of switched capacitors and power relay switches. Existing series switches increase ESR by about 10 times or even more. This dramatically lowers the resonator quality factor Q, resulting in about three times lower field values for a given input power. The switched capacitor solution has other serious drawbacks. Each switched capacitor block is much larger than a fixed capacitor, which will result in issues related to physically accommodating all components. On the other hand, for a relay with an exceptionally small contact resistance of 5 mΩ, Q will change by a factor of 0.6 at 100 kHz and 0.3 at 10 kHz. As the relays cycle, their contact resistance may go up significantly, especially if we do not follow the guidelines for minimum switched current (to create an arc that cleans the contacts). Thus, Q could continue dropping with cycling. Therefore, we plan to implement low-ESR mechanically replaceable bolted-joints based fixed-capacitor banks. The frequency-switching operation will take approximately 3 h.

5.5 Conclusion

In this technical study, we described a whole-body noncontact subthreshold electromagnetic stimulation device based on the concept of a familiar MRI RF resonating coil, but at a much lower resonant frequency (100–150 kHz and potentially down to 10 kHz), with a field modulation option (0.5–100 Hz), and with an input power level of up to 3 kW. Its unique features include a relatively high electric field level within the subject’s biological tissue due to the resonant effect but at low power dissipation, or SAR level, in the body itself.

We emphasize that in the low-frequency limit and at moderate field levels, SAR rather weakly correlates with the deposited electric field. One reason for this is that SAR is proportional to the field squared, and is thus quite small at moderate and low field levels. A second reason is that the tissue conductivity itself is lower (at 100 kHz, it is twice as low as at 100 MHz for muscle and five times lower for fat [105]).

Due to the large resonator volume and its noncontact nature, the subject may be conveniently located anywhere within the resonating coil over a prolonged period of time at moderate and safe electric field levels. The electric field effect does not depend on a particular body position within the resonator. The field penetration is deep everywhere in the body, including the extremities; muscles, bones, and peripheral tissues are mostly affected. Over a shorter period of time, the electric field levels could be increased to relatively large values with an amplitude of about 1 V/cm.

We envision treatment of chronic pain, and particularly neuropathic pain, as the primary potential clinical application for the device. The device enables whole-body coverage, which could be useful in the treatment of widespread pain conditions, such as painful polyneuropathy or fibromyalgia. In addition, a deeper tissue penetration can be achieved without side-effects caused by high current density in the skin associated with the traditional contact electrodes of TENS. It should be noted that these potential clinical applications are speculative and warrant empirical testing in the future.

Considerable attention has been paid to device safety including both the AC power safety and human exposure to electromagnetic fields. In the former case, we have used inductive coupling, which assures that there is no direct current path from the AC power outlet to the coil. This design enhances overall device safety at any power level, including high-power operation. As with more traditional MRI devices, no large metal objects should be located in the immediate vicinity of the coil.

Human exposure to the electromagnetic field within the coil has been evaluated by performing extensive modeling with two independent numerical methods and with an anatomically realistic multi-tissue human phantom. We have shown that the SAR levels within the body correspond to the safety standards of the International Electrotechnical Commission when the input power level of the amplifier driver does not exceed 3 kW. We have also shown that the electric field levels generally comply with the safety standards of the International Commission on Non-Ionizing Radiation Protection when the input power level of the amplifier driver does not exceed 1.5 kW.

Acknowledgments

The authors are thankful to Dr. James O’Rourke, Dr. John McNeill, Ms. Leah Morales, Mr. Brandon Weyant (all from Worcester Polytechnic Institute), MD Irina V. Zhdanova (ClockCoach), and Dr. Aapo Nummenmaa (Massachusetts General Hospital) for useful discussions. Dr. Deng is supported by the Intramural Research Program of the National Institute of Mental Health, NIH.

Creative Commons

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.