© Springer Nature Switzerland AG 2019
Jiaojiao Jiang, Sheng Wen, Bo Liu, Shui Yu, Yang Xiang and Wanlei ZhouMalicious Attack Propagation and Source IdentificationAdvances in Information Security73https://doi.org/10.1007/978-3-030-02179-5_10

10. Identifying Propagation Source in Time-Varying Networks

Jiaojiao Jiang1 , Sheng Wen1, Shui Yu3, Bo Liu2, Yang Xiang3 and Wanlei Zhou4
(1)
Swinburne University of Technology, Hawthorne, Melbourne, VIC, Australia
(2)
La Trobe University, Bundoora, VIC, Australia
(3)
University of Technology Sydney, Ultimo, NSW, Australia
(4)
Digital Research & Innovation Capability, Swinburne University of Technology, Hawthorn, Melbourne, VIC, Australia
 

Identifying the propagation sources of malicious attacks in complex networks plays a critical role in limiting the damage caused by them through the timely quarantine of the sources. However, the temporal variation in the topology of the underlying networks and the ongoing dynamic processes challenge our traditional source identification techniques which are considered in static networks. In this chapter, we introduce an effective approach used in criminology to overcome the challenges. For simplicity, we use rumor source identification to present the approach.

10.1 Introduction

Rumor spreading in social networks has long been a critical threat to our society [143]. Nowadays, with the development of mobile devices and wireless techniques, the temporal characteristic of social networks (time-varying social networks) has deeply influenced the dynamic information diffusion process occurring on top of them [151]. The ubiquity and easy access of time-varying social networks not only promote the efficiency of information diffusion but also dramatically accelerate the speed of rumor spreading [91, 170].

For either forensic or defensive purposes, it has always been a significant work to identify the source of rumors in time-varying social networks [42]. However, the existing techniques for rumor source identification generally require firm connections between individuals (i.e., static networks), so that administrators can trace back along the determined connections to reach the diffusion sources. For example, many methods rely on identifying spanning trees in networks [160, 178], then the roots of the spanning trees are regarded as the rumor sources. The firm connections between users are the premise of constructing spanning trees in these methods. Some other methods detect rumor sources by measuring node centralities, such as degree, betweenness, closeness, and eigenvector centralities [146, 201]. The individual who has the maximum centrality value is considered as the rumor source. All of these centrality measures are based on static networks. Time-varying social networks, where the involved users and interactions always change, have led to great challenges to the traditional rumor source identification techniques.

In this chapter, a novel source identification method is proposed to overcome the challenges, which consists the following three steps: (1) To represent a time-varying social network, we reduce it to a sequence of static networks, each aggregating all edges and nodes present in a time-integrating window. This is the case, for instance, of rumors spreading in Bluetooth networks, for which the fine-grained temporal resolution is not available, whose spreading can be studied through different integrating windows Δt (e.g., Δt could be minutes, hours, days or even months). In each integrating window, if users did not activate the Bluetooth on their devices (i.e., offline), they would not receive or spread the rumors. If they moved out the Bluetooth coverage of their communities (i.e., physical mobility), they would not receive or spread the rumors. (2) Similar to the detective routine in criminology, a small set of suspects will be identified by adopting a reverse dissemination process to narrow down the scale of the source seeking area. The reverse dissemination process distributes copies of rumors reversely from the users whose states have been determined based on various observations upon the networks. The ones who can simultaneously receive all copies of rumors from the infected users are supposed to be the suspects of the real sources. (3) To determine the real source from the suspects, we employ a microscopic rumor spreading model to analytically estimate the probabilities of each user being in different states in each time window. Since this model allows the time-varying connections among users, it can feature the dynamics of each user. More specifically, assuming any suspect as the rumor source, we can obtain the probabilities of the observed users to be in their observed states. Then, for any suspect, we can calculate the maximum likelihood (ML) of obtaining the observation. The one who can provide the maximum ML will be considered as the real rumor source.

10.2 Time-Varying Social Networks

In this section, we introduce the primer for rumor source identification in time-varying social networks, including the features of time-varying social networks, the state transition of users when they hear a rumor, and the categorization of partial observations in time-varying social networks.

10.2.1 Time-Varying Topology

The essence of social networks lies in its time-varying nature. For example, the neighborhood of individuals moving over a geographic space evolves over time (i.e., physical mobility), and the interaction between the individuals appears and disappears in online social networks (i.e., online/offline) [151]. Time-varying social networks are defined by an ordered stream of interactions between individuals. In other words, as time progresses, the interaction structure keeps changing. Examples can be found in both face-to-face interaction networks [27], and online social networks [170]. The temporal nature of such networks has a deep influence on information spreading on top of them. Indeed, the spreading of rumors is affected by duration, sequence, and concurrency of contacts among people.

Here, we reduce time-varying networks to a series of static networks by introducing a time-integrating window. Each integrating window aggregates all edges and nodes present in the corresponding time duration. In Fig. 10.1, we show an example to illustrate the time-integrating windows. In the time window t − 1 (or, at time t − 1), a rumor started to spread from node S who had interaction with five neighbors in this time window. In the next time window t, nodes B, D and F were successfully infected. In this time window, we notice that node O moved next to B (i.e., physical mobility), and node G had no interaction with its neighbors (i.e., offline). Other examples of physical mobility or online/offline status of nodes can be found in the time window t + 1.
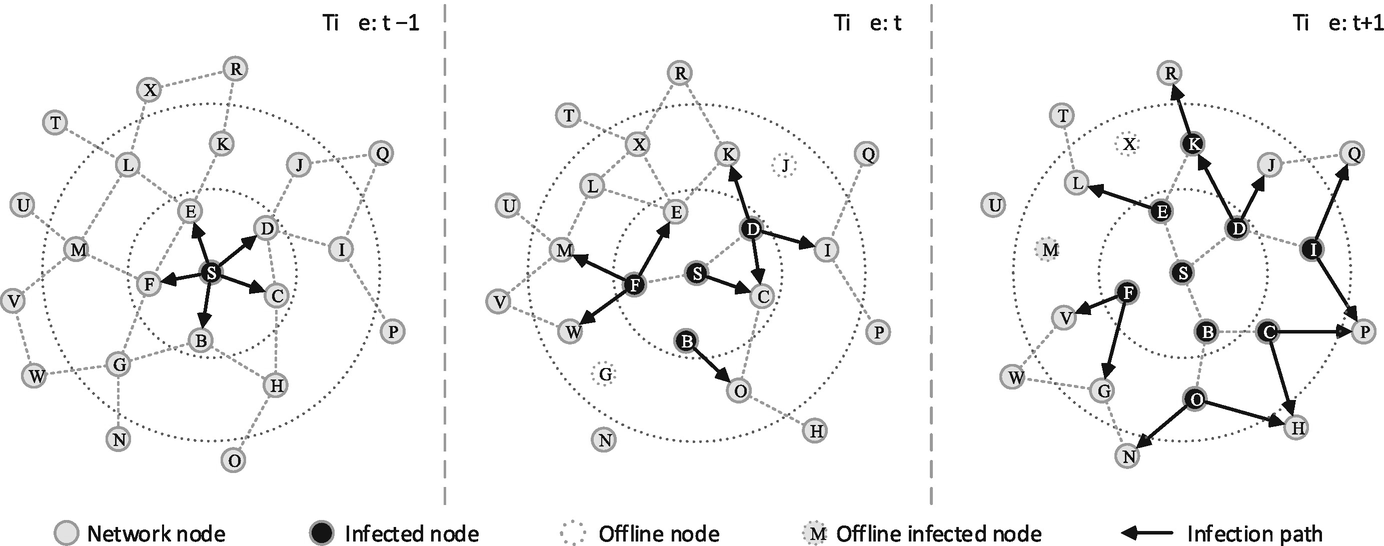
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig1_HTML.png
Fig. 10.1

Example of a rumor spreading in a time-varying network. The random spread is located on the black node, and can travel on the links depicted as line arrows in the time windows. Dashed lines represent links that are present in the system in each time window

10.2.2 Security States of Individuals

For the convenience of description, we borrow the notions from epidemiology to describe the spreading of rumors in time-varying social networks [207]. We say a user is infected when he/she accepts the rumors, and an infected user is recovered if he/she abandons the rumors. In this chapter, we adopt the classic susceptible-infected-recovered (SIR) scheme to present the infection dynamics of each user. Figure 10.2 shows the state transition graph of an arbitrary user in this model. Every user is initially susceptible (Sus.). They can be infected (Inf.) by their neighbors with probability v(i, t), and then recover (Rec.) with probability q(i). Rumors will be spread out from infected users to their social neighbors until they get recovered. There are also many other models of rumor propagation, including the SI, SIS, SIRS models [117, 128]. In present work, we adopt the SIR model because it can reflect the state transition of users when they hear a rumor, from being susceptible to being recovered. Generally, people will not believe the rumor again after they know the truth. Therefore, recovered users will not transit their states any more. For other propagation models, readers can refer to Sect. 10.6 for further discussion.
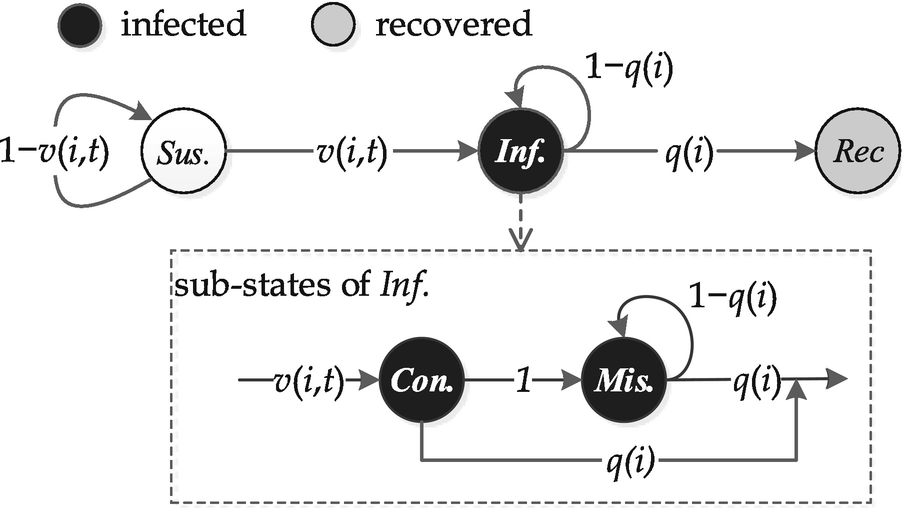
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig2_HTML.png
Fig. 10.2

State transition of a node in rumor spreading model

To more precisely describe node states under different types of observations, we introduce two sub-states of nodes being infected: ‘contagious’ (Con.) and ‘misled’ (Mis.), see Fig. 10.2. An infected node first becomes contagious and then transit to being misled. The Con. state describes the state of nodes newly infected. More specifically, a node is Con. at time t means this node is susceptible at time t − 1 but becomes infected at time t. An misled node will stay being infected until it recovers. For instance, sensors can record the time at which they get infected, and the infection time is crucial in detecting rumor sources because it reflects the infection trend and speed of a rumor. Hence, the introduction of contagious and misled states is intrinsic to the rumor spreading framework.

10.2.3 Observations on Time-Varying Social Networks

Prior knowledge for source identification is provided by various types of partial observations upon time-varying social networks. According to previous work on static networks, we collect three categories of partial observations: wavefronts, snapshots, and sensor observations. We denote the set of observed nodes as O = {o 1, o 2, …, o n}. Following the rumor spreading in Fig. 10.1, we will explain each type of the partial observations as follows.

Wavefront [24]: Given a rumor spreading incident, a wavefront provides partial knowledge of the time-varying social network status. Only the users who are in the wavefront of the spreading can be observed (i.e., all the contagious nodes in the latest time window are observed). Figure 10.3a shows an example of the wavefront in the rumor spreading in Fig. 10.1. We see that nodes C, E, I, K and O are in the wavefront as they transit to being contagious at time t + 1.
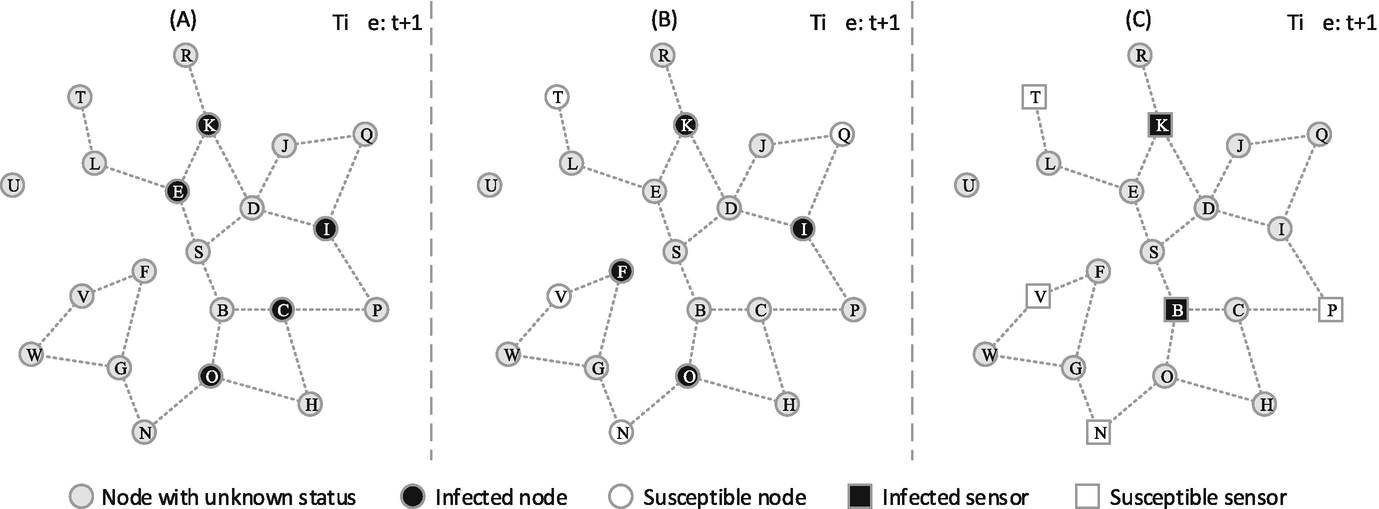
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig3_HTML.png
Fig. 10.3

Three types of observations in regards to the rumor spreading in Fig. 10.1. (a) Wavefront; (b) Snapshot; (c) Sensor observation

Snapshot [115]: Given a rumor spreading incident, a snapshot also provides partial knowledge of the time-varying social network status. In this case, only a group of users can be observed in the latest time window when the snapshot is taken. The states of the observed users can be susceptible, infected or recovered. We use O S, O I and O R to denote the observed users who are susceptible, infected or recovered, respectively. This type of observations is the most common one in our daily life. Figure 10.3b shows an example of the snapshot in the rumor spreading in Fig. 10.1. We see that O S = {N, Q, T, V }, O I = {F, I, K, O} and O R = ∅.

Sensor Observation [146]: Sensors are a group of pre-selected users in time-varying social networks. The sensors can record the rumor spreading dynamics over them, including the security states and the time window when they get infected (more specifically, become contagious). We introduce O S and O I to denote the set of susceptible and infected sensors, respectively. For each o i ∈ O I, the infection time is denoted by t i. This type of observation is usually obtained from sensor networks. Figure 10.3c shows an example of the sensor observations in the rumor spreading in Fig. 10.1. In this case, O S = {N, P, T, V }, O I = {K, B}, and the infection time of node K is t + 1, and node B is infected at time t.

We can see that these three types of partial observations provide three different categories of partial knowledge of the time-varying social network status. Different types of observations are suitable for different circumstances in real-world applications. Readers can refer to [24, 146, 201] for further discussion on different types of partial observations. The partial knowledge together with the time-varying characteristics of social networks make the tracing back of rumor sources much more difficult.

10.3 Narrowing Down the Suspects

Current methods of source identification need to scan every node in the underlying network. This is a bottlenecks of identifying rumor sources: scalability. It is necessary to narrow down a set of suspects, especially in large-scale networks. In this section, we develop a reverse dissemination method to identify a small set of suspects. The details of the method are presented in Sect. 10.3.1, and its efficiency will be evaluated in Sect. 10.3.2.

10.3.1 Reverse Dissemination Method

In this subsection, we first present the rationale of the reverse dissemination method. Then, we show how to apply the reverse dissemination method into different types of partial observations on networks.

10.3.1.1 Rationale

The rationale of the reverse dissemination method is to send copies of rumors along the reversed dynamic connections from observed nodes to exhaust all possible spreading paths leading to the observation. The node from which all the paths, covering all the observed nodes’ states, originated is more likely to be a suspect. The reverse dissemination method is inspired from the Jordan method [201]. The reverse dissemination method is different from the Jordan method, because our method is based on time-varying social networks (involving the physical mobility and online/offline status of users) rather than static networks. In Fig. 10.4, we show a simple example to illustrate the reverse dissemination process. This example follows the rumor spreading in Fig. 10.1 and the wavefront observation in Fig. 10.3a. All wavefront nodes O I = {E, C, I, K, O} observed in time window t + 1 are labeled as black in Fig. 10.4a. The whole process is composed of two rounds of reverse dissemination. In round 1 (Fig. 10.4a), all observed nodes broadcast labeled copies reversely to their neighbors in time window t. For example, nodes S and O received copies of node C (S, O ← C), and node D received copies of three observed nodes C, I and K (D ← C, I, K). In round 2 (Fig. 10.4b), the neighbors who have received labeled copies will relay them to other neighbors in time window t − 1. In each round, the labels will be recorded in each relay node. We can see from Fig. 10.4b that node S has received all copies from all the observed nodes (S ← C, E, K, I, O). Then, node S is chosen to be a suspect.
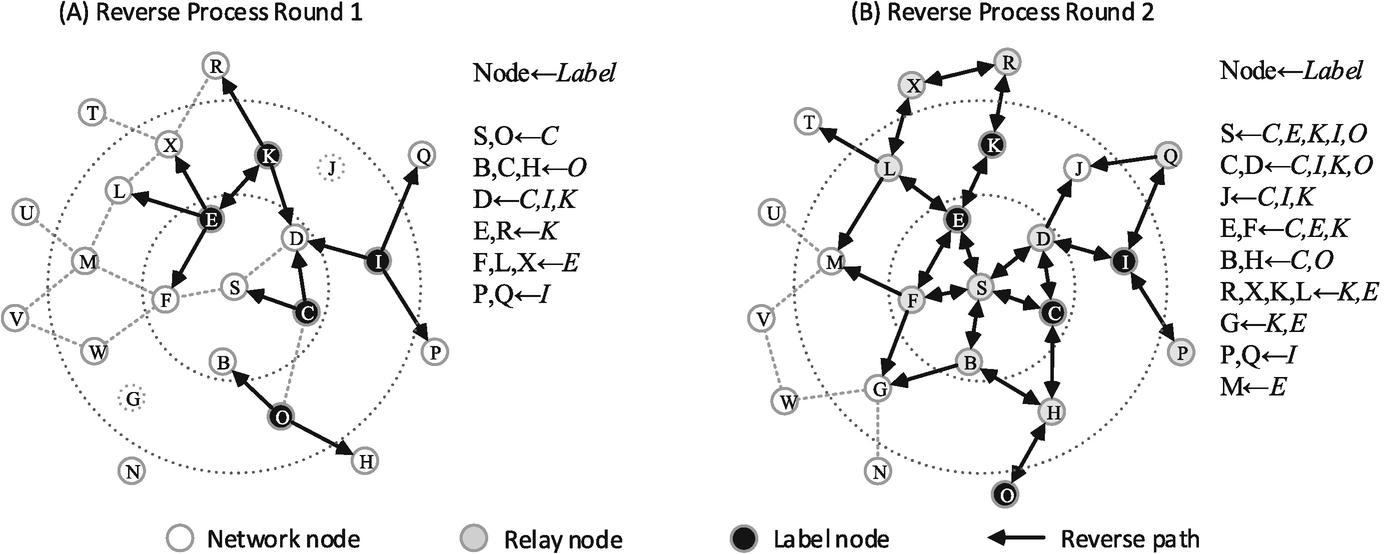
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig4_HTML.png
Fig. 10.4

Illustration of the reverse dissemination process in regards to the wavefront observation in Fig. 10.3a. (a) The observed nodes broadcast labeled copies of rumors to their neighbors in time window t; (b) The neighbors who received labeled copies will relay them to their own neighbors in time window t − 1

We notice that the starting time for each observed node starting their reverse dissemination processes varies in different types of observations. For a wavefront, since all the observed nodes are supposed to be contagious in the latest time window, all the observed nodes need to simultaneously start their reverse dissemination processes. For a snapshot, the observed nodes stay in their states in the latest time window. Therefore, the reverse dissemination processes will also simultaneously starts from all the observed nodes. However, for a sensor observation, because the infected sensors record their infection time, the starting time of reverse dissemination for each sensor will be determined by t i. More specifically, the latest infected sensors first start their reverse dissemination processes, and then the sensors infected in the previous time window, until the very first infected sensors.

10.3.1.2 Wavefront

Given a reverse dissemination process starting from an observed node o i, we use P C(u, t|o i) to denote the probability of an arbitrary node u to be contagious after time t, where t denotes the time span of the whole reverse dissemination process. Let all observed nodes o i start their reverse dissemination processes in the latest time window. To match the wavefront, it is expected a suspect u can simultaneously receive rumor copies from all o i ∈ O (i.e., the rumor copies sent from all observed nodes can make node u become contagious simultaneously). Mathematically, we identify those nodes who can provide the maximum likelihood, L(u, t), of being a suspect receiving copies from all the observed nodes, as in
$$\displaystyle \begin{aligned} L(u,t) = \sum_{o_i\in O}\mbox{ln}(P_C(u,t|o_i)). \end{aligned} $$
(10.1)
For the convenience of computation, we adopt logarithmic function ln(⋅) in Eq. (10.1) to derive the maximum likelihood. We use U to denote the set of suspects. The ones who provide larger values of L(u, t) are recognized as a member of set U.

10.3.1.3 Snapshot

To match the snapshot observation (which includes susceptible, infected or recovered nodes), it is expected that a suspect u needs to satisfy the following three principles at time t. First, copies of rumors disseminated from observed susceptible nodes o i ∈ O S cannot reach node u at time t (i.e., u is still susceptible). Second, copies of rumors disseminated from observed infected nodes o j ∈ O I can reach node u at time t (i.e., u becomes infected). Third, copies of rumors disseminated from observed recovered nodes o k ∈ O R can arrive at node u before time t (i.e., u becomes recovered). Again, we employ maximum likelihood to capture this kind of nodes, as in
$$\displaystyle \begin{aligned} \begin{aligned} L(u,t)=& \sum_{o_i\in O_S}\mbox{ln}(P_S(u,t|o_i))+\sum_{o_j\in O_I}\mbox{ln}(P_I(u,t|o_j))\\ &+\sum_{o_k\in O_R}\mbox{ln}(P_R(u,t|o_k)),\\ \end{aligned} \end{aligned} $$
(10.2)
where P S(u, t|o i), P I(u, t|o i) and P R(u, t|o i) denote the probabilities of u to be susceptible, infected or recovered after time t, respectively, given that the reverse dissemination started from o i.

10.3.1.4 Sensor

For sensor observations, according to our previous discussion, we let infected sensor o i ∈ O I start to reversely disseminate copies of the rumor at time $$\hat {t}_i=T-t_i$$ , where T = max{t i|o i ∈ O I}. We also let the susceptible sensors o j ∈ O S start to reversely disseminate copies of rumors at time t=0. To match a sensor observation, it is expected a suspect u needs to satisfy the following two principles at time t. First, copies of rumors disseminated from susceptible sensors o i ∈ O S cannot reach node u at time t (i.e., node u is still susceptible). Second, copies of rumors disseminated from all infected sensors o j ∈ O I can be received by node u at time t (i.e., node u becomes contagious). Mathematically, we determine the suspects by computing their maximum likelihood, as in
$$\displaystyle \begin{aligned} \begin{aligned} L(u,t) = &\sum_{o_i\in O_I}\mbox{ln}(P_C(u,t+\hat{t}_i|o_i))\\ &+\sum_{o_j\in O_S}\mbox{ln}(P_S(u,t|o_j)). \end{aligned} \end{aligned} $$
(10.3)

The values of P S(u, t|o i), P C(u, t|o i), P I(u, t|o i) and P R(u, t|o i) will be calculated by the model introduced in Sect. 10.4.2. We summarize the reverse dissemination method in Algorithm 10.1.

Algorithm 10.1: Reverse dissemination

../images/466717_1_En_10_Chapter/466717_1_En_10_Figa_HTML.gif

10.3.2 Performance Evaluation

We evaluate the performance of the reverse dissemination method in real time-varying social networks. Similar to Lokhov et al.’s work [108], we consider the infection probabilities and recovery probabilities to be uniformly distributed in (0,1), and the average infection and recovery probabilities are set to be 0.6 and 0.3. We also use α to denote the ratio of suspects over all nodes, α = |U|∕N, where N is the number of all nodes in a time-varying social network. The value of α ranges from 5% to 100%. We randomly choose the real source in 100 runs of each experiment. The number of 100 comes from the work in [207].

We consider four real time-varying social networks in Table 10.1: The MIT reality [46] dataset captures communication from 97 subjects at MIT over the course of the 2004–2005 academic year. The Sigcom09 [145] dataset contains the traces of Bluetooth device proximity of 76 persons during SIGCOMM 2009 conference in Barcelona, Spain. The Enron Email [164] dataset contains record of email conversations from 143 users in 2001. The Facebook [171] dataset contains communications from 45,813 users during December 29th, 2008 and January 3rd, 2009. All of these datasets reflect the physical mobility and online/offline features of time-varying social networks. According to the study in [151], an appropriate temporal resolution Δt is important to correctly characterize the dynamical processes on time-varying networks. Therefore, we need to be cautious when we choose the time interval of size Δt. Furthermore, many social networks have been shown small-world, i.e., the average distance l between any two nodes is small, generally l ≤ 6. Previous extensive works show that rumors can spread quickly in social networks, generally after 6–10 time ticks of propagation (see [42]). Hence, we divided the social networks into 6–10 time windows. Therefore, for the datasets used in this chapter, we uniformly divide each into 6–10 discrete time windows [151]. For other division of temporal resolution, readers could refer to [151] for further discussion.
Table 10.1

Comparison of data collected in the experiments

Dataset

MIT

Sigcom09

Email

Facebook

Device

Phone

Phone

Laptop

Laptop

Network type

Bluetooth

Bluetooth

WiFi

WiFi

Duration (days)

246

5

14

6

# of devices

97

76

143

45,813

# of contacts

54,667

69,189

1246

264,004

Figure 10.5 shows the experiment results in the four real datasets. We find the proposed method works quite well in reducing the number of suspects. Especially for snapshots, the searching scale can be narrowed to 5% of all users for the MIT dataset, 15% for the Sigcom09 dataset, and 20% for the Enron Email and Facebook datasets. The number of suspects can be reduced to 45% of all users in the MIT reality dataset under snapshot and wavefront observations. For the Enron Email and Facebook datasets, the number of suspects can be reduced to 20% of all users. The worst case occurred in the Sigcom09 dataset with wavefronts, but our method still achieved a reduction of 35% in the total number of users.
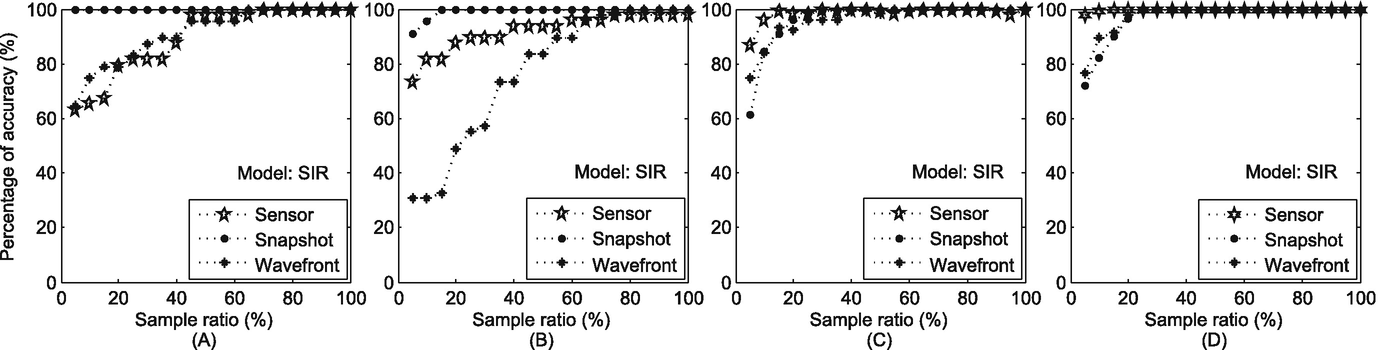
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig5_HTML.png
Fig. 10.5

Accuracy of the reverse dissemination method in networks. (a) MIT; (b) Sigcom09; (c) Enron Email; (d) Facebook

The experiment results on real time-varying social networks show that the proposed method is efficient in narrowing down the suspects. Real-world social networks usually have a large number of users. Our proposed method addresses the scalability in source identification, and therefore is of great significance.

10.4 Determining the Real Source

Another bottleneck of identifying rumor sources is to design a good measure to specify the real source. Most of the existing methods are based on node centralities, which ignore the propagation probabilities between nodes. Some other methods consider the BFS trees instead of the original networks. These violate the rumor spreading processes. In this section, we adopt an innovative maximum-likelihood based method to identify the real source from the suspects. A novel rumor spreading model will also be introduced to model rumor spreading in time-varying social networks.

10.4.1 A Maximum-Likelihood (ML) Based Method

10.4.1.1 Rationale

The key idea of the ML-based method is to expose the suspect from set U that provides the largest maximum likelihood to match the observation. It is expected that the real source will produce a rumor propagation which not only temporally but also spatially matches the observation more than other suspects. Given an observation O = {o 1, o 2, …, o n} in a time-varying network, we let the spread of rumors start from an arbitrary suspect u ∈ U from the time window that is t u before the latest time window. For an arbitrary observed node o i, we use P S(o i, t u|u) to denote the probability of o i being susceptible at time t u, given that the spread of rumors starts from suspect u. Similarly, we have P C(o i, t u|u), P I(o i, t u|u) and P R(o i, t u|u) representing the probabilities of o i being contagious, infected and recovered at time t u, respectively. We use $$\tilde {L}(t_u,u)$$ to denote the maximum likelihood of obtaining the observation when the rumor started from suspect u. Among all the suspects in U, we can estimate the real source by choosing the maximum value of the ML, as in
$$\displaystyle \begin{aligned} (u^*, t^*) = \mbox{arg max}_{u\in U}\tilde{L}(t_{u},u). \end{aligned} $$
(10.4)
The result of Eq. (10.4) suggests that suspect u ∗ can provide a rumor propagation not only temporally but also spatially matches the observation better than other suspects. We also have an estimation of infection scale I(t ∗, u ∗) as a byproduct, as in
$$\displaystyle \begin{aligned} I(t^*,u^*) = \sum_{i=1}^NP_I(i,t^*|u^*). \end{aligned} $$
(10.5)
Later, we can justify the effectiveness of the ML-based method by examining the accuracy of t ∗ and I(t ∗, u ∗).

10.4.1.2 Wavefront

In a wavefront, all observed nodes are contagious in the time window when the wavefront is captured. Supposing suspect u is the rumor source, the maximum likelihood $$\tilde {L}(t_u,u)$$ of obtaining the wavefront O is the product of the probabilities of any observed node o i ∈ O being contagious after time t u. We also adopt a logarithmic function to present the computation of the maximum likelihood. Then, we have $$\tilde {L}(t_u,u)$$ for a wavefront, as in
$$\displaystyle \begin{aligned} \tilde{L}(t_u,u) = \sum_{o_i\in O}\mbox{ln}(P_C(o_i,t_u|u)). \end{aligned} $$
(10.6)

10.4.1.3 Snapshot

In a snapshot, the observed nodes can be susceptible, infected or recovered in the time window when the snapshot is taken. Supposing suspect u is the rumor source, the maximum likelihood of obtaining the snapshot is the product of the probabilities of any observed node o i ∈ O being in its observed state. Then, we have the logarithmic form of the calculation for $$\tilde {L}(t_u,u)$$ in a snapshot, as in
$$\displaystyle \begin{aligned} \begin{aligned} &\tilde{L}(t_u,u) = \sum_{o_i\in O_S}\mbox{ln}(P_S(o_i,t_u|u))+\\ &\sum_{o_j\in O_I}\mbox{ln}(P_I(o_j,t_u|u))+\sum_{o_k\in O_R}\mbox{ln}(P_R(o_k,t_u|u)). \end{aligned} \end{aligned} $$
(10.7)

10.4.1.4 Sensor

In a sensor observation, each infected sensor o i ∈ O I records its infection time t i. Although the absolute time t i cannot directly suggest the spreading time of the rumor, we can derive the relative infection time of each sensor. Supposing suspect u is the rumor source, for an arbitrary infected sensor o i, its relative infection time is $$\tilde {t}_i=t_i-\tilde {t}+t_u$$ where $$\tilde {t}=\mbox{min}\{t_i|o_i\in O_I\}$$ , and t u is obtained from Algorithm 10.1. For suspect u ∈ U, the maximum likelihood $$\tilde {L}(t_u,u)$$ of obtaining the observation is the product of the probability of any sensor o i to be in its observed state at time $$\tilde {t}_i$$ . Then, we have the logarithmic form of the calculation for $$\tilde {L}(t_u,u)$$ in a sensor observation, as in
$$\displaystyle \begin{aligned} {\tilde{L}(t_u,u) = \sum_{o_i\in O_I}\mbox{ln}(P_C(u,\tilde{t}_i|o_i)) +\sum_{o_j\in O_S}\mbox{ln}(P_S(u,t_u|o_j))}. \end{aligned} $$
(10.8)
Note that, P S(u, t|o i), P C(u, t|o i), P I(u, t|o i), and $$P_R(\tilde {u},t|o_i)$$ can be calculated in the rumor spreading model in Sect. 10.4.2. We summarize the method of determining rumor sources in Algorithm 10.2.

Algorithm 10.2: Targeting the suspect

../images/466717_1_En_10_Chapter/466717_1_En_10_Figb_HTML.gif

10.4.2 Propagation Model

In this subsection, we introduce an analytical model to present the spreading dynamics of rumors in time-varying social networks. The state transition of each node follows the SIR scheme introduced in Sect. 10.2.2. For rumor spreading processes among users, we use this model to calculate the probabilities of each user in various states.

In the modeling, every user is initially susceptible. We use η ji(t) to denote the spreading probability from user j to user i in time window t. Then, we can calculate the probability of a susceptible user being infected by his/her infected neighbors as in
$$\displaystyle \begin{aligned} v(i,t) = 1 - \prod_{j\in N_i}[1-\eta_{ji}(t)\cdot P_I(j,t-1)], \end{aligned} $$
(10.9)
where, N i denotes the set of neighbors of user i. Then, we can compute the probability of an arbitrary user to be susceptible at time t as in
$$\displaystyle \begin{aligned} P_S(i,t) = [1-v(i,t)]\cdot P_S(i,t-1). \end{aligned} $$
(10.10)
Once a user gets infected, he/she becomes contagious. We then have the probability that an arbitrary user is contagious at time t as in
$$\displaystyle \begin{aligned} P_C(i,t) = v(i,t)\cdot P_S(i,t-1). \end{aligned} $$
(10.11)
Since an infected user can be either contagious or misled, we can obtain the value of P I(i, t) as in
$$\displaystyle \begin{aligned} P_I(i,t) = P_C(i,t) + (1-q_i(t))\cdot P_I(i,t-1). \end{aligned} $$
(10.12)
Then, the value of the P R(i, t) can be derived from
$$\displaystyle \begin{aligned} P_R(i,t) = P_R(i,t-1) + q_i(t)\cdot P_I(i,t-1). \end{aligned} $$
(10.13)
This model analytically derives the probabilities of each user in various states in an arbitrary time t. This in addition constitutes the maximum likelihood L(u, t) of an arbitrary user u being a suspect in time window t in Sect. 10.3.1. This also supports the calculation of the maximum likelihood $$\tilde {L}(t,u)$$ to match the observation in time window t, given that the rumor source is the suspicious user u in Sect. 10.4.1.

10.5 Evaluation

In this section, we evaluate the efficiency of our source identification method. The experiment settings are the same as those presented in Sect. 10.3.2. Specifically, we let the sampling ratio α range from 10% to 30%, as the reverse dissemination method has already achieved a good performance with α dropping in this range.

10.5.1 Accuracy of Rumor Source Identification

We evaluate the accuracy of our method in this subsection. We use δ to denote the error distance between a real source and an estimated source. Ideally, we have δ = 0 if our method accurately captures the real source. In practice, we expect that our method can accurately capture the real source or a user very close to the real source (i.e., δ is very small). As the user close to the real source usually has similar characteristics with the real source, quarantining or clarifying rumors at this user is also very significant to diminish the rumors [160].

Our method shows good performances in the four real time-varying social networks. Figure 10.6 shows the frequency of the error distances (δ) in the MIT reality dataset under different categories of observations. When the sampling ratio α ≥ 20%, our method can identify the real sources with an accuracy of 78% for the sensor observations, more than 60% for the snapshots, and around 36% for the wavefronts. For the wavefronts, although our method cannot identify real sources with very high accuracy, the estimated sources are very close to the real sources, and are generally 0–2 hops away. Figure 10.7 shows the frequency of the error distances δ in the Sigcom09 dataset. When the sampling ratio α ≥ 20%, the proposed method can identify the real sources with an accuracy of more than 70% for the snapshots. For the other two categories of observations, although our method cannot identify real sources with very high accuracy, the estimated sources are very close to the real sources, with an average of 1–2 hops away in the sensor observations, and 1–3 hops away for the wavefronts. Figure 10.8 shows the performance of our method in the Enron Email dataset. When the sampling ratio α ≥ 20%, our method can identify the real sources with an accuracy of 80% for the snapshots, and more than 45% for the wavefronts. The estimated sources are very close to the real sources, with an average 1–3 hops away in the sensor observations. Figure 10.9 shows the performance of our method in the Facebook dataset. Similarly, when the sampling ratio α ≥ 20%, the proposed method can identify the real sources with an accuracy of around 40% for the snapshots. The estimated sources are very close to the real sources, with an average of 1–3 hops away from the real sources under the sensor and wavefront observations.
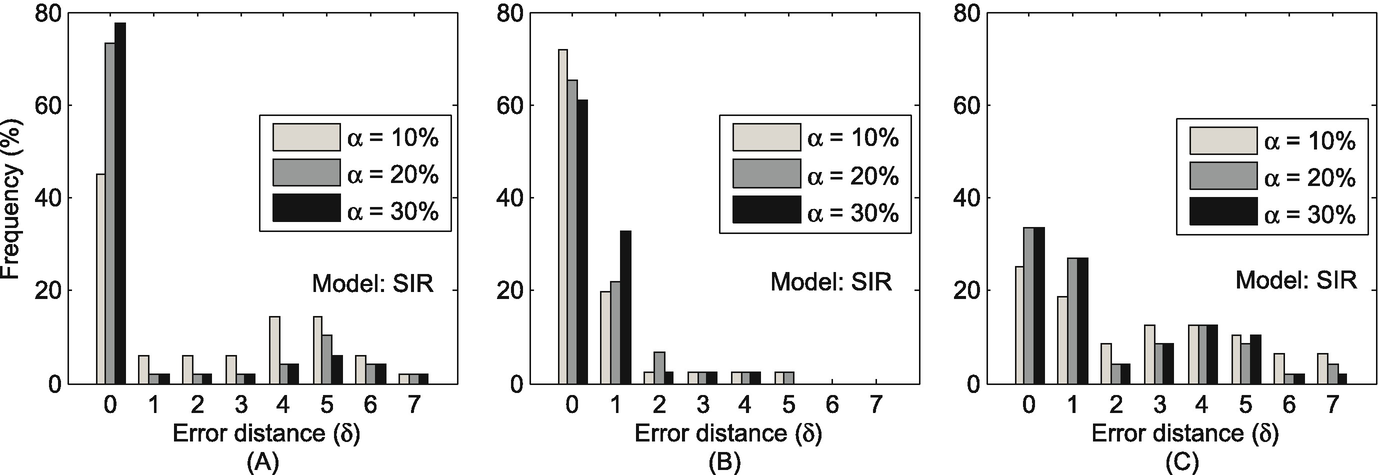
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig6_HTML.png
Fig. 10.6

The distribution of error distance (δ) in the MIT Reality dataset. (a) Sensor; (b) Snapshot; (c) Wavefront

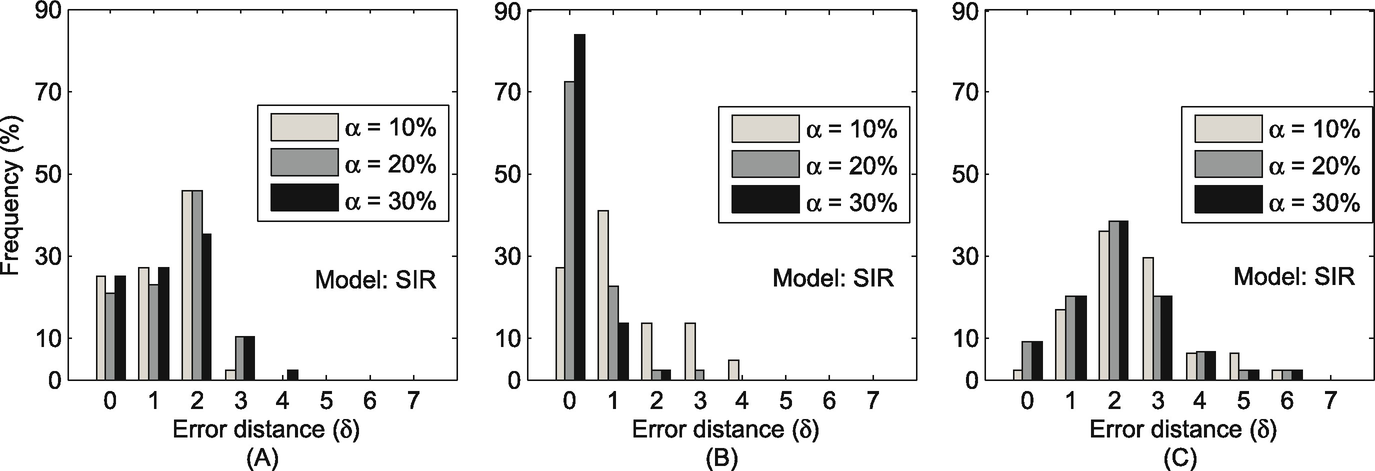
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig7_HTML.png
Fig. 10.7

The distribution of error distance (δ) in the Sigcom09 dataset. (a) Sensor; (b) Snapshot; (c) Wavefront

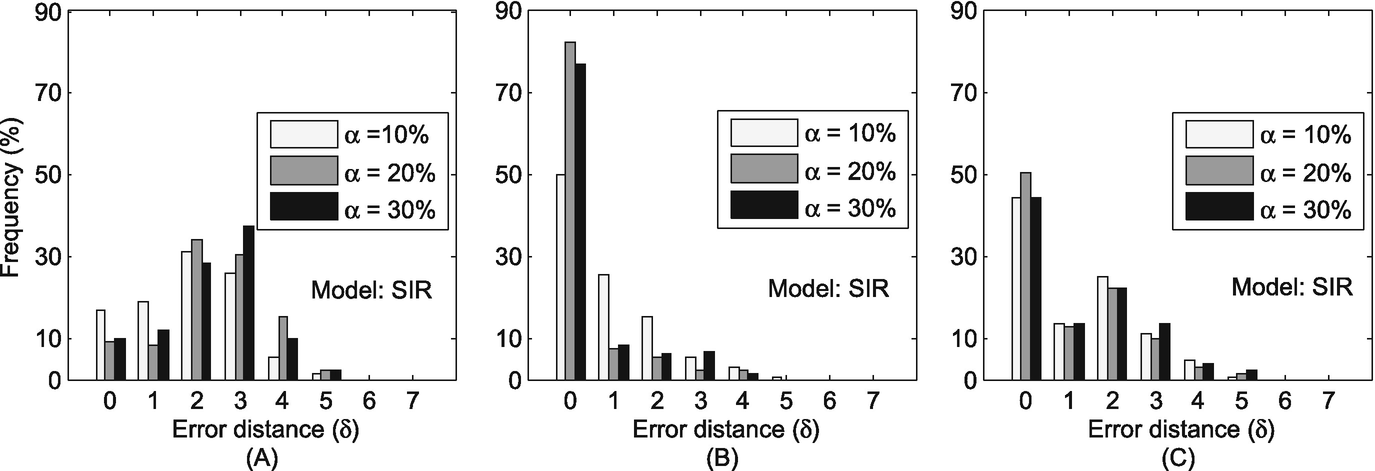
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig8_HTML.png
Fig. 10.8

The distribution of error distance (δ) in the Enron Email dataset. (a) Sensor; (b) Snapshot; (c) Wavefront

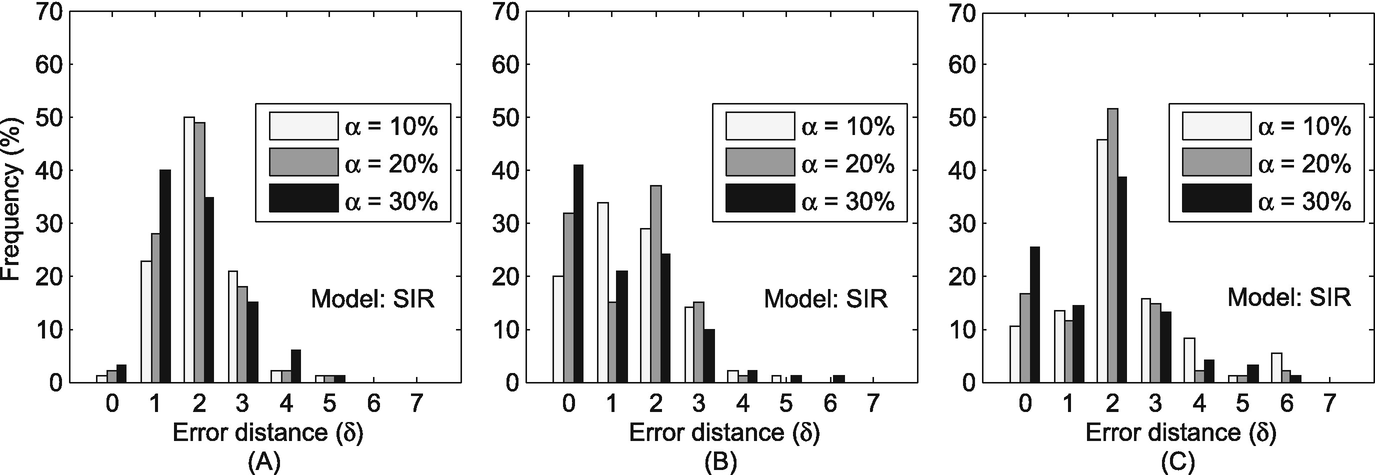
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig9_HTML.png
Fig. 10.9

The distribution of error distance (δ) in the Facebook dataset. (a) Sensor; (b) Snapshot; (c) Wavefront

Compared with previous work, our proposed method is superior because our method can work in time-varying social networks rather than static networks. Our method can achieve around 80% of all experiment runs that accurately identify the real source or an individual very close to the real source. However, the previous work of [178] has theoretically proven their accuracy was at most 25% or 50% in tree-like networks, and their average error distance is 3–4 hops away.

10.5.2 Effectiveness Justification

We justify the effectiveness of our ML-based method from three aspects: the correlation between the ML of the real sources and that of the estimated sources, the accuracy of estimating rumor spreading time, and the accuracy of estimating rumor infection scale.

10.5.2.1 Correlation Between Real Sources and Estimated Sources

We investigate the correlation between the real sources and the estimated sources by examining the correlation between their maximum likelihood values. For different types of observation, the maximum likelihood of an estimated source can be obtained from Eqs. (10.6), (10.7) or Eq. (10.8), i.e., $$\tilde {L}(t^*,u^*)$$ . The maximum likelihood of a real source is obtained by replacing u ∗ and t ∗ as the real source and the real rumor spreading time, respectively. If the estimated source is in fact the real source, their maximum likelihood values should present high correlation.

The correlation results of the maximum likelihood values when α = 20% in the four time-varying social networks are shown from Figs. 10.10, 10.11, 10.12, 10.13. We see that the maximum likelihood values of the real sources and that of the estimated sources are highly correlated with each other. Their maximum likelihood values approximately form linear relationships to each other. Figure 10.10 shows the results in the MIT reality dataset. We can see that the maximum likelihood values of the real sources and that of the estimated sources are highly correlated in both sensor and snapshot observations. The worst results occurred in wavefront observations, however the majority of the correlation results still tend to be clustered in a line. These exactly reflect the accuracy of identifying rumor sources in Fig. 10.6. The results in the Sigcom09 dataset are shown in Fig. 10.11. We see that the maximum likelihood values are highly correlated in both snapshot and wavefront observations. The worst results occurred in sensor observations, however the majority of the correlation results still tend to be clustered in a line. These exactly reflect the accuracy of identifying rumor sources in Fig. 10.7. The results in the Enron Email dataset are shown in Fig. 10.12. We see that the maximum likelihood values are highly correlated in both snapshot and wavefront observations, and slightly correlated in sensor observations. These exactly reflect the accuracy of identifying rumor sources in Fig. 10.8. Similar results can be found in the Facebook dataset in Fig. 10.13, which precisely reflects the accuracy of identifying rumor sources in Fig. 10.9.
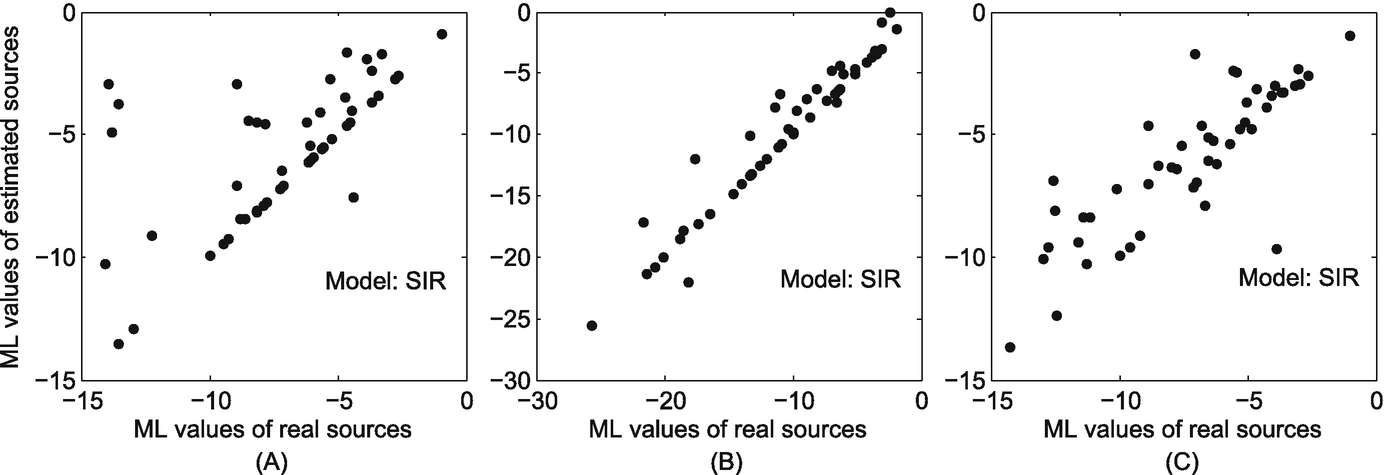
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig10_HTML.png
Fig. 10.10

The correlation between the maximum likelihood of the real sources and that of the estimated sources in the MIT reality dataset. (a) Sensor observation; (b) Snapshot observation; (c) Wavefront observation

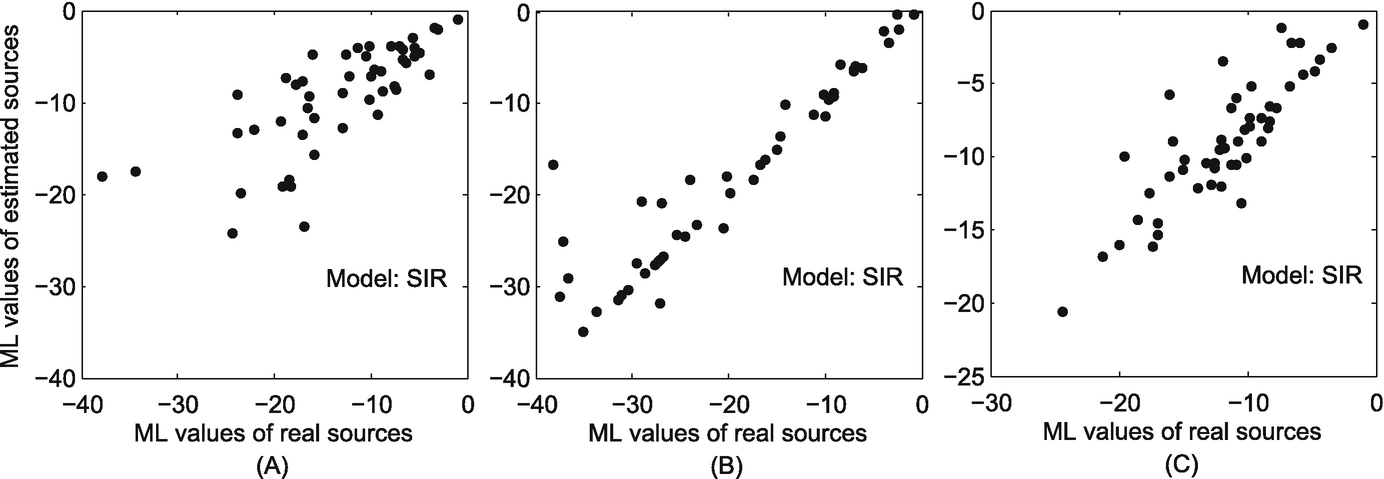
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig11_HTML.png
Fig. 10.11

The correlation between the maximum likelihood of the real sources and that of the estimated sources in the Sigcom09 dataset. (a) Sensor observation; (b) Snapshot observation; (c) Wavefront observation

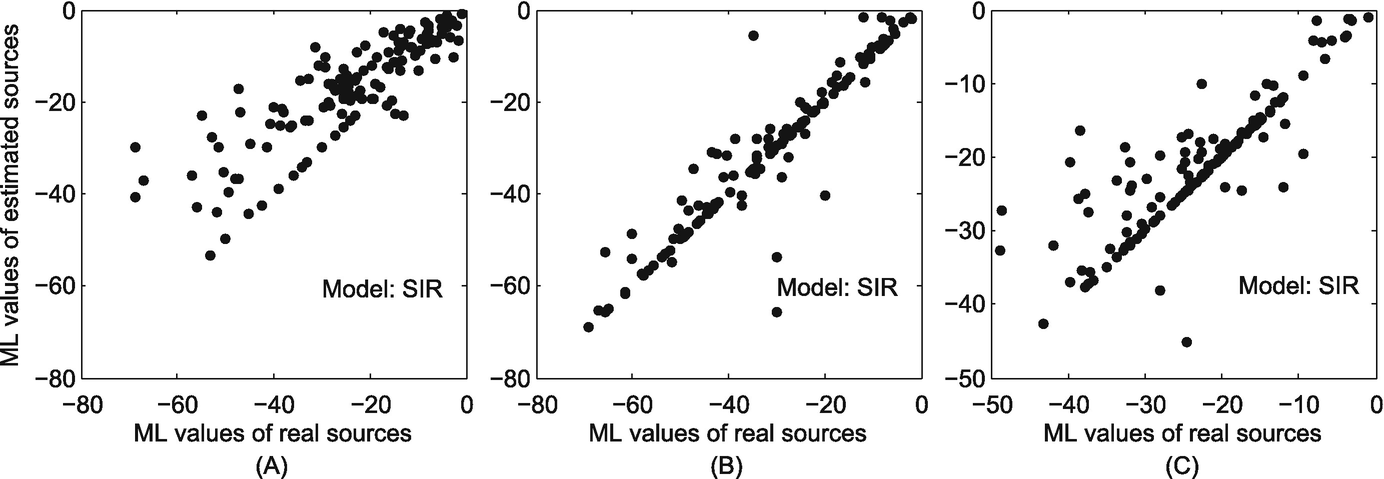
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig12_HTML.png
Fig. 10.12

The correlation between the maximum likelihood of the real sources and that of the estimated sources in the Enron Email dataset. (a) Sensor observation; (b) Snapshot observation; (c) Wavefront observation

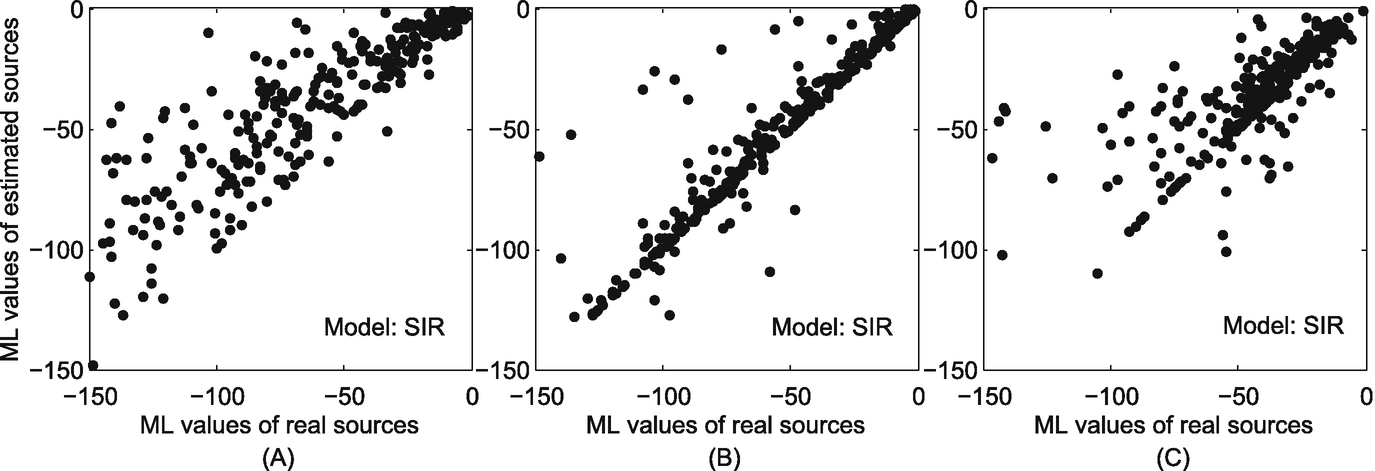
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig13_HTML.png
Fig. 10.13

The correlation between the maximum likelihood of the real sources and that of the estimated sources in the Facebook dataset. (a) Sensor observation; (b) Snapshot observation; (c) Wavefront observation

The strong correlation between the ML values of the real sources and that of the estimated sources in time-varying social networks reflects the effectiveness of our ML-based method.

10.5.2.2 Estimation of Spreading Time

As a byproduct, our ML-based method can also estimate the spreading time (in Eq. (10.4)) of rumors. In order to justify the effectiveness of our proposed method, we further investigate the effectiveness of this byproduct. We expect the estimate can accurately expose the real spreading time of rumors. We let the real spreading time vary from 2 to 6 in four real time-varying social networks. The experiment results are shown in Table 10.2.
Table 10.2

Accuracy of estimating rumor spreading time

Environment settings

Estimated spreading time

Observation

T

MIT

Sigcom09

Email

Facebook

Sensor

2

2± 0

2±0

2±0

1.787±0.411

 

4

4.145± 0.545

3.936± 0.384

4.152± 0.503

3.690± 0.486

 

6

6.229±0.856

5.978±0.488

6.121±0.479

5.720±0.604

Snapshot

2

1.877±0.525

2.200±1.212

2.212±0.781

2.170±0.761

 

4

3.918± 0.862

3.920± 0.723

3.893± 0.733

4.050± 0.716

 

6

6.183±1.523

6.125±1.330

5.658±1.114

5.650±1.266

Wavefront

2

2±0

2±0

2±0

1.977±0.261

 

4

4.117± 0.686

4± 0

3.984± 0.590

4.072± 0.652

 

6

6±0

5.680±1.096

5.907± 0.640

5.868±0.864

As shown in Table 10.2, we analyze the means and the standard deviations of the estimated spreading time. We see that the means of the estimated spreading time are very close to the real spreading time, and most results of the standard deviations are smaller than 1. Especially when the spreading time T = 2, our ML-based method in sensor observations and wavefront observations can accurately estimate the spreading time in the MIT reality, Sigcom09 and Enron Email datasets. The results are also quite accurate in the Facebook dataset. From Table 10.2, we can see that our method can estimate the spreading time with extremely high accuracy in wavefront observations, and relatively high accuracy in snapshot observations.

Both the means and standard deviations indicate that our method can estimate the real spreading time with high accuracy. The accurate estimate of the spreading time indicates that our method is effective in rumor source identification.

10.5.2.3 Estimation of Infection Scale

We further justify the effectiveness of our ML-based method by investigating its accuracy in estimating the infection scale of rumors provided by the second byproduct in Eq. (10.5). We expect that the ML-based method can accurately estimate the infection scale of each propagation incident. Particularly, we let the rumor spreading initiate from the node with largest degree in each full time-varying social network and spread for six time windows in experiments.

In Fig. 10.14, we show the real infection scales at each time tick, and also the estimated infection scales in different types of observations. We can see that the proposed method can provide a fairly accurate estimate of on the infection scales of rumors in the MIT reality dataset, the Sigcom09 dataset and the Facebook dataset in different types of observations. As shown in Fig. 10.14c, the worst result occurred in the Enron Email dataset after time tick 4. According to our investigation, this was caused by a great deal of infected nodes that tend to be in the recovered stage in the SIR scheme, which leads to a fairly large uncertainty in the estimate.
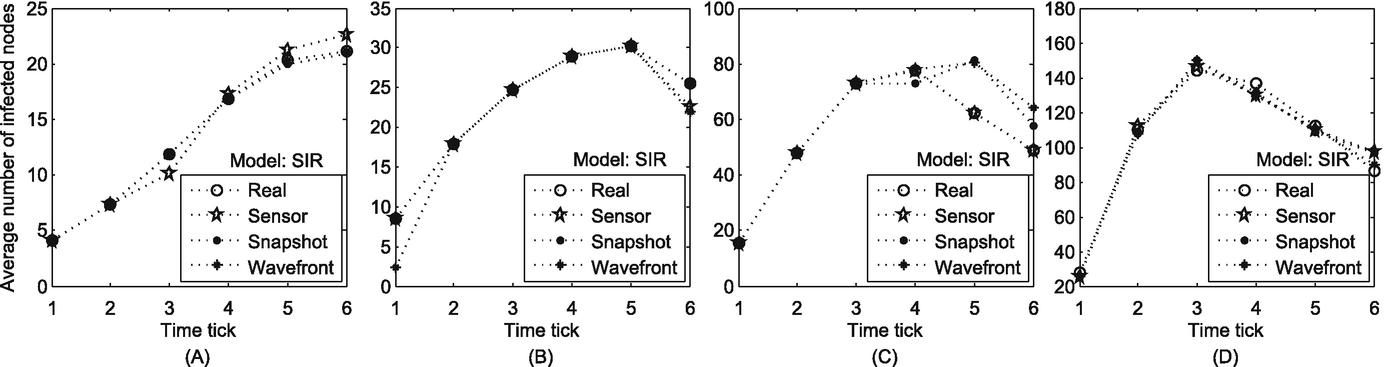
../images/466717_1_En_10_Chapter/466717_1_En_10_Fig14_HTML.png
Fig. 10.14

The accuracy of estimating infection scale in real networks. (a) MIT; (b) Sigcom09; (c) Enron Email; (d) Facebook

To summarize, all of the above evaluations reflect the effectiveness of our method from different aspects: the high correlation between the ML values of the real sources and that of the estimated sources, the high accuracy in estimating spreading time of rumors, and the high accuracy of the infection scale.

10.6 Summary

In this chapter, we explore the problem of rumor source identification in time-varying social networks that can be reduced to a series of static networks by introducing a time-integrating window. In order to address the challenges posted by time-varying social networks, we adopted two innovative methods. First, we utilized a novel reverse dissemination method which can sharply narrow down the scale of suspicious sources. This addresses the scalability issue in this research area and therefore dramatically promotes the efficiency of rumor source identification. Then, we introduced an analytical model for rumor spreading in time-varying social networks. Based on this model, we calculated the maximum likelihood of each suspect to determine the real source from the suspects. We conduct a series of experiments to evaluate the efficiency of our method. The experiment results indicate that our methods are efficient in identifying rumor sources in different types of real time-varying social networks.

There is some future work can be done in identifying rumor sources in time-varying networks. There are also many other models of rumor propagation, such as the models in [117, 128]. These models can be basically divided into two categories: the macroscopic models and the microscopic models. The macroscopic models, which are based on differential equations, only provide the overall infection trend of rumor propagation, such as the total number of infected nodes [207]. The microscopic models, which are based on difference equations, not only provide the overall infection status of rumor propagation, but they also can estimate the probability of an arbitrary node being in an arbitrary state [146]. In the field of identifying propagation sources, researchers generally choose microscopic models, because it requires to estimate which specific node is the first one getting infected. As far as we know, so far there is no work that is based on the macroscopic models to identify rumor sources in social networks. Future work may also investigate combining microscopic and macroscopic models, or even adopting the mesoscopic models [118, 124], to estimate both the rumour sources and the trend of the propagation. There are also many other microscopic models other than the SIR model adopted in this chapter, such as the SI, SIS, and SIRS models [146, 201]. As we discussed in Sect. 10.2.2, people generally will not believe the rumor again after they know the truth, i.e., after they get recovered, they will not transit to other states. Thus, the SIR model can reflect the state transition of people when they hear a rumor. We also evaluate the performance of the proposed method on the SI model. Since the performance of our method on the SI model is similar to that on the SIR model, we only present the results on the SIR model in this chapter.