© Springer Nature Switzerland AG 2019
Jiaojiao Jiang, Sheng Wen, Bo Liu, Shui Yu, Yang Xiang and Wanlei ZhouMalicious Attack Propagation and Source IdentificationAdvances in Information Security73https://doi.org/10.1007/978-3-030-02179-5_11

11. Identifying Multiple Propagation Sources

Jiaojiao Jiang1 , Sheng Wen1, Shui Yu3, Bo Liu2, Yang Xiang3 and Wanlei Zhou4
(1)
Swinburne University of Technology, Hawthorne, Melbourne, VIC, Australia
(2)
La Trobe University, Bundoora, VIC, Australia
(3)
University of Technology Sydney, Ultimo, NSW, Australia
(4)
Digital Research & Innovation Capability, Swinburne University of Technology, Hawthorn, Melbourne, VIC, Australia
 

The global diffusion of epidemics, computer viruses and rumors causes great damage to our society. One critical issue to identify the multiple diffusion sources so as to timely quarantine them. However, most methods proposed so far are unsuitable for diffusion with multiple sources because of the high computational cost and the complex spatiotemporal diffusion processes. In this chapter, we introduce an effective method to identify multiple diffusion sources, which can address three main issues in this area: (1) How many sources are there? (2)Where did the diffusion emerge? (3) When did the diffusion break out? For simplicity, we use rumor source identification to present the approach.

11.1 Introduction

With the rapid urbanization and advancements in communication technologies, the world has become more interconnected. This not only makes our daily life more convenient, but also has made us vulnerable to new types of diffusion risks. These diffusion risks arise in many different contexts. For instance, infectious diseases, such as SARS [123], H1N1 [62] or Ebola [168], have spread geographically and killed hundreds of thousands or even millions of people. Computer viruses, like Cryptolocker and Alureon, cause a good share of cyber-security incidents [119]. In the real world, rumors often emerge from multiple sources and spread incredibly fast in complex networks [62, 123, 142, 168]. After the initial outbreak of rumor diffusion, the following three issues often attract people’s attention: (1) How many sources are there? (2) Where did the diffusion emerge? and (3) When did the diffusion breakout?

In the past few years, researchers have proposed a series of methods to identify rumor diffusion sources in networks. These methods mainly focus on the identification of a single diffusion source in networks. For example, Shah and Zaman [160] proposed a rumor-center method to identify rumor sources in networks under complete observations. Essentially, they consider the rumor source as the node that has the maximum number of distinct propagation paths to all the infected nodes. Zhu and Ying [203] proposed a Jordan-center method, which utilizes a sample path based approach, to detect diffusion sources in tree networks with snapshot observations. Luo et al. [115] derived the Jordan-center method based on a different approach. Shah and Zaman [161] proved that, even in tree networks, the rumor source identification problem is a #P-complete problem, which is at least as hard as the corresponding NP problem. The problem becomes even harder for generic networks. However, due to the extreme complexity of the spatiotemporal rumor propagation process and the underlying network structure, few of existing methods are proposed for identifying multiple diffusion sources. Luo et al. [114] proposed a multi-rumor-center method to identify multiple rumor sources in tree-structured networks. The computational complexity of this method is O(n k), where n is the number of infected nodes and k is the number of sources. It is too computationally expensive to be applied in large-scale networks with multiple diffusion sources. Chen et al. [32] extended the Jordan-center method from single source detection to the identification of multiple sources in tree networks. However, the topologies of real-world networks are far more complex than trees. Fioriti et al. [58] introduced a dynamic age method to identify multiple diffusion sources in general networks. They claimed that the ‘oldest’ nodes, which were associated to those with largest eigenvalues of the adjacency matrix, were the sources of the diffusion. Similar work to this technique can be found in [148]. However, an essential prerequisite is that we need to know the number of sources in advance.

In this chapter, we introduce a novel method, K-center, to identify multiple rumor sources in general networks. In the real world, the rumor diffusion processes in networks are spatiotemporally complex because of the combined multi-scale nature and intrinsic heterogeneity of the networks. To have a clear understanding of the complex diffusion processes, we adopt a measure, effective distance, recently proposed by Brockmann and Helbing [24]. The concept of effective distance reflects the idea that a small propagation probability between neighboring nodes is effectively equivalent to a large distance between them, and vice versa. By using effective distance, the complex spatiotemporal diffusion processes can be reduced to homogeneous wave propagation patterns [24]. Moreover, the relative arrival time of diffusion arriving at a node is independent of diffusion parameters but linear with the effective distance between the source and the node of interest. For multi-source diffusion, we obtain the same linear correlation between the relative arrival time and the effective distance of any infected node. Thereby, supposing that any node can be infected very quickly, an arbitrary node is more likely to be infected by its closest source in terms of effective distance. Therefore, to identify multiple diffusion sources, we need to partition the infection graph so as to minimize the sum of effective distances between any infected node and the corresponding partition center. The final partition centers are viewed as diffusion sources.

The contribution of this part of work is threefold corresponding to the three key issues of rumor source identification problem:

  • We propose a fast method to identify multiple rumor diffusion sources. Based on this method, we can determine where the diffusion emerged. We prove that the proposed method is convergent and the computational complexity is O(mnlogα), where α = α(m, n) is the slowly growing inverse-Ackermann function, n is the number of infected nodes, and m is the number of edges connecting them.

  • According to the topological positions of the detected rumor sources, we derive an efficient algorithm to estimate the spreading time of the diffusion.

  • When the number of sources is unknown, we develop an intuitive and effective approach that can estimate the number of diffusion sources with high accuracy.

11.2 Preliminaries

In this section, we introduce preliminary knowledge used in this chapter, including the analytic epidemic model [207] and the concept of effective distance [24]. For convenience, we borrow notions from the area of epidemics to represent the states of nodes in a network [186]. A node being infected stands for a person getting infected by a disease, viruses having compromised a computer, or a user believing a rumor. Readers can derive analogous meanings for a node being susceptible or recovered.

11.2.1 The Epidemic Model

We adopt the classic susceptible-infected (SI) model to present the diffusion dynamics of each node. Figure 11.1 shows the state transition graph of a node in this model.
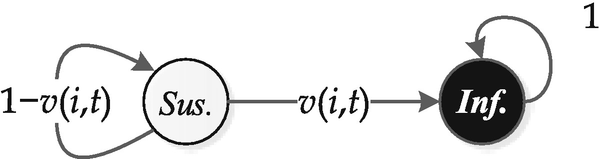
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig1_HTML.png
Fig. 11.1

The state transition graph of a node in the SI model

As shown in Fig. 11.1, every node is initially susceptible (Sus.). An arbitrary susceptible node i can be infected (Inf.) by its already-infected neighbors with probability v(i, t) at time t. Therefore, we can compute the probability of node i to be susceptible at time t as in
$$\displaystyle \begin{aligned} P_S(i, t) = [1 - v(i, t)] \cdot P_S(i, t - 1). \end{aligned} $$
(11.1)
Then, we can obtain the probability of node i to be infected at time t as in
$$\displaystyle \begin{aligned} P_I(i, t) = v(i, t) \cdot P_S(i, t - 1) + P_I (i, t - 1). \end{aligned} $$
(11.2)
We use η ji to denote the propagation probability from node j to its neighboring node i. Then, we can calculate the probability of node i being infected by its neighbors as in
$$\displaystyle \begin{aligned} v(i, t) = 1-\Pi_{j\in N_i} [1 - \eta_{ji}\cdot P_I(j, t - 1)], \end{aligned} $$
(11.3)
where N i denotes the set of neighbors of node i. This model analytically derives the probability of each node in various states at an arbitrary time. To address real problems, the length of each time tick relies on the real environment. It can be 1 min, 1 h or 1 day. We also need to set the propagation probability η ij between nodes properly.

11.2.2 The Effective Distance

Brockmann and Helbing [24] recently proposed a new measure, effective distance, which can disclose the hidden pattern geometry of complex diffusion. The effective distance from a node i to a neighboring node j is defined as
$$\displaystyle \begin{aligned} e(i,j) = 1 - \mbox{log}\eta_{ij}, \end{aligned} $$
(11.4)
where η ij is again the propagation probability from i to j. This concept reflects the idea that a small propagation probability from i to j is effectively equivalent to a large distance between them, and vice versa. To illustrate this measure, a simple example is shown in Fig. 11.2. For instance, the propagation probability is 0.8 between node S and A, and is only 0.1 between S and B (see Fig. 11.2a). Correspondingly, the effective distance between S and A is 1.22 which is much less than that between S and B (see Fig. 11.2b).
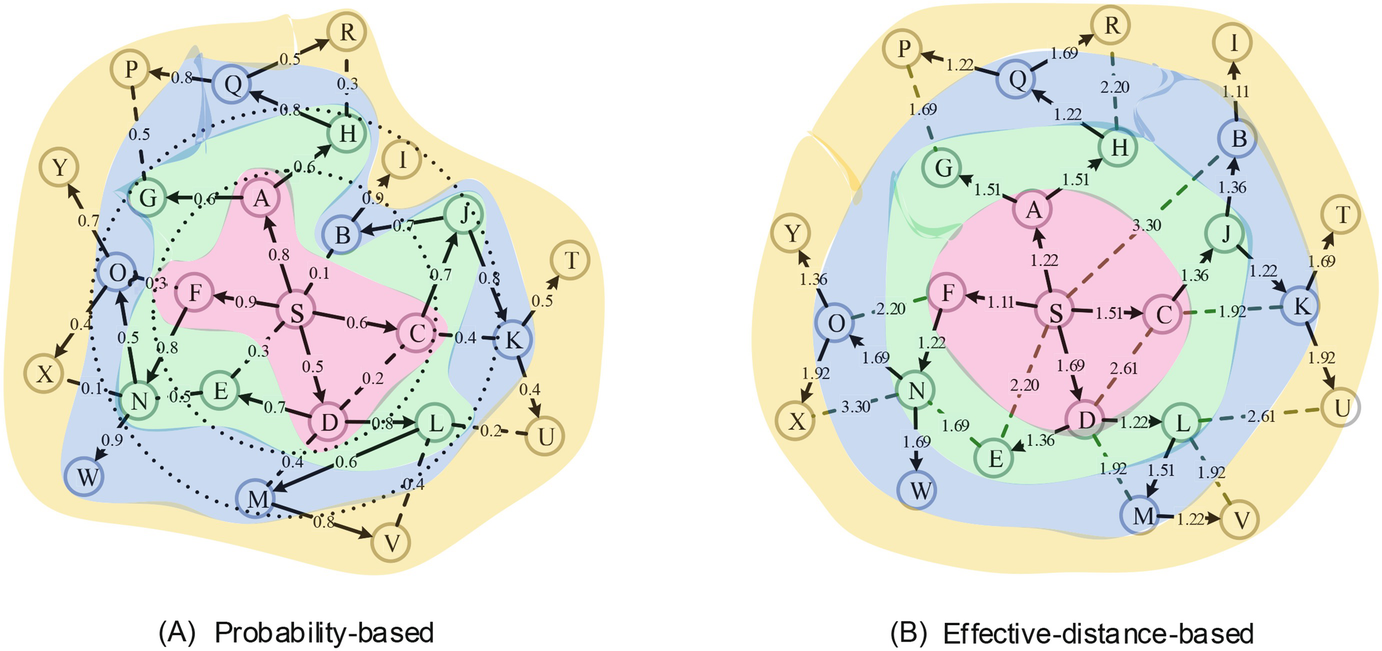
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig2_HTML.png
Fig. 11.2

An example of altering an infection graph using effective distance. (a) An example infection graph with source S. The weight on each edge is the propagation probability. The two dot circles represent the first-order and second-order neighbors of source S. The colors indicate the infection order of nodes, e.g., nodes A, C, D and F are infected after the first time tick. Notice that the diffusion process is spatiotemporally complex. (b) The altered infection graph. The weight on each edge is the effective distance between the corresponding end nodes. Notice that the effective distances from source S to the infected nodes can accurately reflect their infection orders

Based on the effective distances between neighboring nodes, the length λ( Γ) of a path Γ = {u 1, …, u L} is defined as the sum of effective lengths along the edges of the path. Moreover, the effective distance from an arbitrary node i to another node j is defined by the length of the shortest path in terms of effective distance from node i to node j, i.e.,
$$\displaystyle \begin{aligned} d(i,j) = \mbox{min}_{\Gamma}\lambda(\Gamma), \end{aligned} $$
(11.5)

From the perspective of diffusion source s, the set of shortest paths in terms of effective distance to all the other nodes constitutes a shortest path tree Ψs. Brockmann and Helbing obtain that the diffusion process initiated from node s on the original network can be represented as wave patterns on the shortest path tree Ψs. In addition, they conclude that the relative arrival time of the diffusion arriving at a node is independent of diffusion parameters and is linear with the effective distance from the source to the node of interest.

In this chapter, we will alter the original network by utilizing effective distance through converting the propagation probability on each edge to the corresponding effective distance. Then, by using the linear relationship between the relative arrival time and the effective distance of any infected node, we derive a novel method to identify multiple diffusion sources.

11.3 Problem Formulation

Before we present the problem formulation derived in this chapter, we firstly show an alternate expression of an arbitrary infection graph by using effective distance (see again Fig. 11.2). Figure 11.2a shows an example of an infection graph with diffusion source S. The colors indicate the infection order of nodes (e.g., nodes A, C, D and F were infected after the first time tick T = 1, similarly for the other nodes). Notice that the diffusion process is spatiotemporally complex, because the first-order neighbors of source S can be infected after the second time tick (e.g., node E) or even the third time tick (e.g., node B), similarly for the second-order and third-order neighbors. We then alter the infection graph by replacing the weight on each edge with the effective distance between the corresponding end nodes (see Fig. 11.2b). We notice that the effective distances from source S to all the infected nodes can accurately reflect the infection order of them. This exactly shows that the relative arrival time of an arbitrary node getting infected is linear with the effective distance between the source and the node of interest.

Suppose that at time T = 0, there are k(≥ 1) sources, S ∗ = {s 1, …, s k}, starting the diffusion simultaneously [58, 115]. Several time ticks after the diffusion started, we got n infected nodes. These nodes form a connected infection graph G n, and each source s i has its infection region C i(⊆ G n). Let $$\mathcal {C}^{*}=\cup _{i=1}^k C_i$$ be a partition of the infection graph such that C i ∩ C j = ∅. for i ≠ j. Each partition C i is a connected subgraph in G n and consists of the nodes whose infection can be traced back to the source node s i. For an arbitrary infected node v j ∈ C i, suppose it can be infected in the shortest time, then according to our previous analysis, it will have shorter effective distance to source s i than to any other source. Therefore, we need to divide the infection graph G n into k partitions so that each infected node belongs to the partition with the shortest effective distance to the partition center. The final partition centers are considered as the diffusion sources.

Given an infection graph G n, from the above analysis, we know that our goal is to identify a set of diffusion sources S ∗ and the corresponding partition $$\mathcal {C}^*$$ of the infection graph G n. To be precise, we aim to find a partition $$\mathcal {C}^*$$ of G n, to minimize the following objective function,
$$\displaystyle \begin{aligned} \mbox{min}_{\mathcal{C}^*} f = \sum_{i=1}^k\sum_{v_j\in C_i}d(v_j, s_i), \end{aligned} $$
(11.6)
where node v j belongs to partition C i associated with source s i, and d(v j, s i) is the shortest-path distance in terms of effective distance between v j and s i.

Equation (11.6) is the proposed formulation for multi-source identification problem. Since, we need to find out the k centers of the diffusion from Eq. (11.6), we name the proposed method of solving the multi-source identification problem as the K-center method, which we will detail in the following section.

11.4 The K-Center Method

In this section, we propose a K-center method to identify multiple diffusion sources and the corresponding infection regions in general networks. We firstly introduce a method for network partition. Then, we derive the K-center method. Secondly, according to the estimated sources, we derive an algorithm to predict the spreading time of the diffusion. Finally, we present a heuristic algorithm to estimate the diffusion sources when the number of sources is unknown.

11.4.1 Network Partitioning with Multiple Sources

Given an infection network G n and a set of sources S ∗ = {s 1, …, s k}, network partition refers to the division of a network into k partitions with s i(i ∈{1, 2, …, k}) as the partition centers. According to our previous analysis in Sect. 11.3, an arbitrary node v j ∈ G n should be classified into partition C i associated with source s i, such that
$$\displaystyle \begin{aligned} d(v_j , s_i) = \mbox{min}_{s_l\in S} d(v_j , s_l). \end{aligned} $$
(11.7)
In essence, for an arbitrary node v j ∈ G n, it needs to be associated to source s i that is the nearest source to v j. This is similar to the Capacity Constrained Network-Voronoi Diagram (CCNVD) problem [195]. Given a graph and a set of service centers, the CCNVD partitions the graph into a set of contiguous service areas that meet service center capacities and minimize the sum of the distances (min-sum) from graph nodes to allotted service centers. The CCNVD problem is important for critical societal applications such as assigning evacuees to shelters and assigning patients to hospitals.

In this chapter, to satisfy Eq. (11.7), we utilize the Voronoi strategy to partition the altered infection graph obtained from Sect. 11.3. The detailed Voronoi partition process is shown in Algorithm 11.1. Future work may use community structure for network partition. Current methods for detecting community structure include strategies based on betweenness [72], information theory [152], and modularity optimization [132].

Algorithm 11.1: Network partition

../images/466717_1_En_11_Chapter/466717_1_En_11_Figa_HTML.gif

11.4.2 Identifying Diffusion Sources and Regions

In this subsection, we present the K-center method to identify multiple diffusion sources. According to the objective function in Eq. (11.6), we need to find a partition $$\mathcal {C}^*$$ of the altered infection graph G n, which can minimize the sum of the effective distances between each infected node and its corresponding partition center. From the previous subsection, if we randomly choose a set of sources S, Voronoi partition can split the network into subnets such that each node is associated with its nearest source. Thus, Voronoi partition can find a local optimal partition of G n with a fixed set of sources S. However, to optimize the partition $$\mathcal {C}^*$$ , we need to adjust the center of each partition so as to minimize the objective function in Eq. (11.6). In this chapter, we adjust the center of each partition by choosing a new center as the node that has the minimum sum of effective distances to all the other nodes in the partition. Therefore, we call this method as the K-center method. This is similar to the rumor-center method and the Jordan-center method that consider rumor centers or Jordan centers as the diffusion sources. As the name suggests, the K-center method is more specific to the multi-source identification. The detailed process of the K-center method is shown in Algorithm 11.2.

Algorithm 11.2: K-center to identify multiple sources

../images/466717_1_En_11_Chapter/466717_1_En_11_Figb_HTML.gif

The following two theorems show the convergence of the proposed K-center method and its computational complexity.

Theorem 11.1

The objective function in Eq.(11.6) is monotonically decreasing in iterations. Therefore, the K-center method is convergent.

Proof

Suppose that at iteration t, $$S_t = \{s^t_1, \ldots , s^t_k\}$$ are the estimated sources. We then use Algorithm 11.1 to partition the infection graph G n as $$\mathcal {C}^t = \cup _{i=1}^k C_i^k$$ . Thus, the objective function at iteration t becomes
$$\displaystyle \begin{aligned} f^t = \sum_{i=1}^k\sum_{v_j\in C^t_i} d(v_j, s^t_i). \end{aligned} $$
(11.11)
At the next iteration t + 1, according to the K-center method, we recalculate the center of each partition $$C^t_i$$ and obtain $$S^{t+1} = \{s^{t+1}_1, \ldots , s^{t+1}_k\}$$ , such that
$$\displaystyle \begin{aligned} \sum_{v_j\in C^t_i} d(v_j, s^{t+1}_i)\leq \sum_{v_j\in C^t_i} d(v_j, s^{t}_i). \end{aligned} $$
(11.12)
Then, the objective function becomes
$$\displaystyle \begin{aligned} \tilde{f}^t = \sum_{i=1}^k\sum_{v_j\in C^t_i} d(v_j, s^{t+1}_i). \end{aligned} $$
(11.13)
From Eqs. (11.11) and (11.12), we notice that
$$\displaystyle \begin{aligned} \tilde{f}^t \leq f^t. \end{aligned} $$
(11.14)
We then re-partition the infection graph G n with centers $$S^{t+1} = \{s^{t+1}_1, \ldots , s^{t+1}_k\}$$ such that each infected node v j ∈ G n will be associated to a nearest center $$s^{t+1}_i$$ , and obtain a new partition $$\mathcal {C}^{t+1} = \cup _{i=1}^k C^{t+1}_i$$ of G n. Thus, the objective function at iteration t + 1 becomes
$$\displaystyle \begin{aligned} f^{t+1} = \sum_{i=1}^k\sum_{v_j\in C^{t+1}_i} d(v_j, s^{t+1}_i). \end{aligned} $$
(11.15)
Since each node is classified to the nearest $$s^{t+1}_i$$ , we see that
$$\displaystyle \begin{aligned} f^{t+1} \leq \tilde{f}^t. \end{aligned} $$
(11.16)
From Eqs. (11.14) and (11.16), we have
$$\displaystyle \begin{aligned} f^{t+1} \leq \tilde{f}^t \leq f^t. \end{aligned} $$
(11.17)
Therefore, the objective function in Eq. (11.6) is monotonically decreasing, i.e., the K-center method is convergent.

Theorem 11.2

Given a infection graph G n with n nodes and m edges, the computational complexity of the K-center method is O(mnlogα), where α = α(m, n) is the very slowly growing inverse-Ackermann function [ 144 ].

Proof

From Algorithm 11.2, we know that the main difficulty of the K-center method stems from the calculation of the shortest paths between node pairs in the altered infection graph G n. Other computation in this algorithm can be treated as a constant. In this chapter, we adopt the Pettie-Ramachandran algorithm [144], to compute all-pairs shortest paths in G n. The computational complexity of the algorithm is O(mnlogα), where α = α(m, n) is the very slowly growing inverse-Ackermann function [144]. Therefore, we have proved the theorem.

According to Theorem 11.1, we know that the proposed K-center method is well defined. We notice that the rationale of the K-center method is similar to that of the K-means algorithm in the data-mining field. Similar to the K-means algorithm, there is no guarantee that a global minimum in the objective function will be reached. From Theorem 11.2, We see that the computational complexity of the K-center method is much less than the method in [115] with O(n k), and much less than the method in [58] with O(n 3). In addition, the proposed method can be applied in general networks, whereas the other methods mainly focus on trees. Comparatively, the proposed method is more efficient and practical in identifying multiple diffusion sources in large networks.

11.4.3 Predicting Spreading Time

Given an infection graph G n, we can obtain a partition $$C^* = \cup _{i=1}^k C_i$$ of G n and the corresponding partition centers S ∗ by using the proposed K-center method. According to the SI model in Sect. 11.2.1, the spreading time of diffusion can be estimated by the total number of time ticks of the diffusion. Then, we can predict the spreading time based on the hops between the source and the infected nodes in each partition. For an arbitrary source s i associated with partition C i and an arbitrary node v j ∈ C i, we introduce h(s i, v j) to denote the minimum number of hops between s i and v j. Therefore, the spreading time in each partition can be estimated as in
$$\displaystyle \begin{aligned} t_i = \mbox{max}\{h(s_i, v_j)|v_j\in C_i\}, i\in\{1, \ldots , k\}. \end{aligned} $$
(11.18)
Then, the spreading time of the whole diffusion is as in
$$\displaystyle \begin{aligned} T = \mbox{max}\{t_i|i = 1, \ldots , k\}. \end{aligned} $$
(11.19)
The spreading time T based on hops has simplified the modeling process. In the real world, the spreading time of different paths with the same number of hops may vary from each other. We have solved this temporal problem of the SI model in another chapter [186]. In this field, the majority of current modeling is based on spreading hops [176]. To be consistent with previous work, we adopt the simplified hop-based SI model to study the source identification problem.

11.4.4 Unknown Number of Diffusion Sources

In most practical applications, the number of diffusion sources is unknown. In this subsection, we present a heuristic algorithm that allows us to estimate the number of diffusion sources.

Algorithm 11.3: K-center identification with unknown number of sources

../images/466717_1_En_11_Chapter/466717_1_En_11_Figc_HTML.gif

From Sect. 11.4.3, we know that if the number of sources k is given, we can estimate the spreading time T (k) using Eq. (11.19). To estimate the number of diffusion sources, we let k start from 1 and compute the spreading time T (1). Then, we increase the number of sources k by 1 in each iteration and compute the corresponding spreading time T (k) until we find T (k) = T (k+1), i.e., the spreading time of the diffusion stays the same when the number of sources increases from k to k + 1. That is to say when the number of sources increases from k to k + 1, they can lead to the same infection graph G n. We then choose the number of diffusion sources as k (or k + 1). The detailed process of the K-center method with unknown number of sources is shown in Algorithm 11.3. We evaluate this heuristic algorithm in Sect. 11.5.2.

To address real problems, we firstly need to get the underlying network over which the real diffusion spreads. Secondly, we need to measure the propagation probability on each edge in the network. Thirdly, according to the SI model in Sect. 11.2.1, we need to specify the length of one time tick of the diffusion properly. All of this information is crucial to source identification. However it requires big effort to obtain.

11.5 Evaluation

In this section, we evaluate the proposed K-center method in three real network topologies: the North American Power Grid [180], the Yeast protein-protein interaction network [82], and the Facebook network [171]. The Facebook network topology is crawled from December 29th, 2008 to January 3rd, 2009. The basic statistics of these networks are shown in Table 11.1, and their degree distributions are shown in Fig. 11.3. We adopt the classic SI model, and suppose all infections are independent of each other. In simulations, we typically set the propagation probability on each edge, η ij, uniformly distributed in (0, 1). As previous work [186, 207] has proven that the distribution of propagation probability will not affect the accuracy of the SI model, uniform distribution is enough to evaluate the performance of the proposed method. Similar propagation probability setting can be found in [116, 203] and [32]. We randomly choose a set of sources S ∗, and let the number of diffusion sources |S ∗| range from 2 to 5. For each type of network and each number of diffusion sources, we perform 100 runs. The number of 100 comes from the discussion in the previous work of [207]. The implementation is in C++ and Matlab2012b.
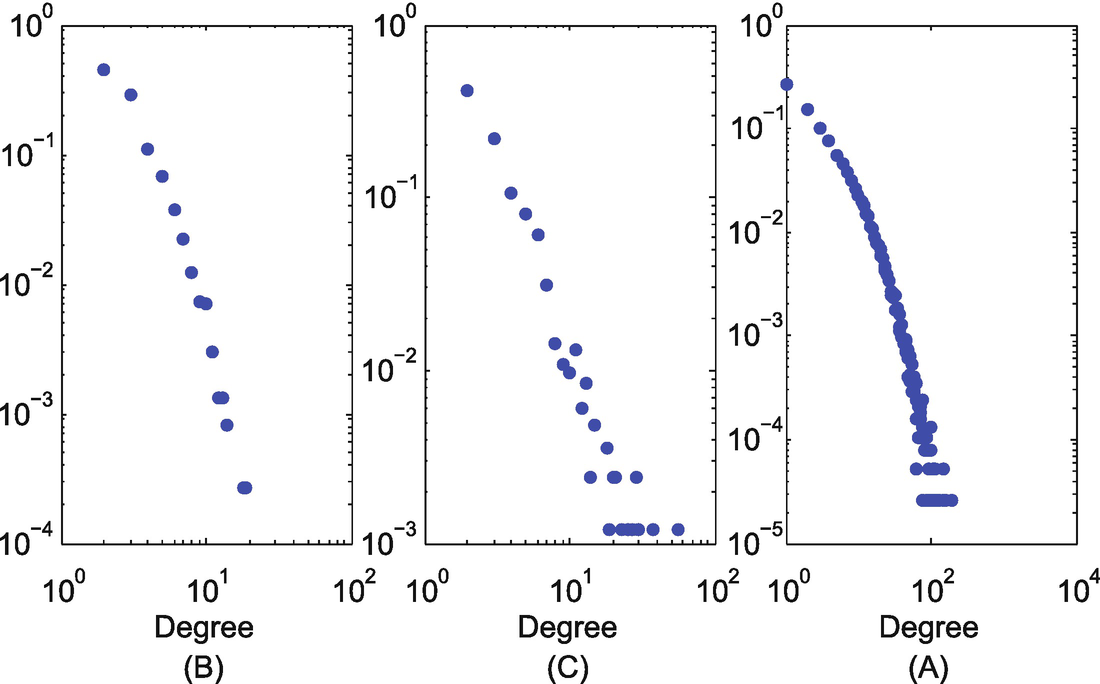
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig3_HTML.png
Fig. 11.3

Degree distribution. (a) Power grid; (b) Yeast; (c) Facebook

Table 11.1

Statistics of the datasets collected in experiments

Dataset

Power grid

Yeast

Facebook

# nodes

4941

2361

45,813

# edges

13,188

13,554

370,532

Average degree

2.67

5.74

8.09

Maximum degree

19

64

223

We firstly show the convergence of the proposed method. Figure 11.4 shows the objective function values in iterations when the number of sources is 2 in the three real network topologies. It can be seen that the objective function is monotonically decreasing in iterations. Similar results can be found when we choose different number of sources. This, therefore, justifies Theorem 11.1 in Sect. 11.4.2.
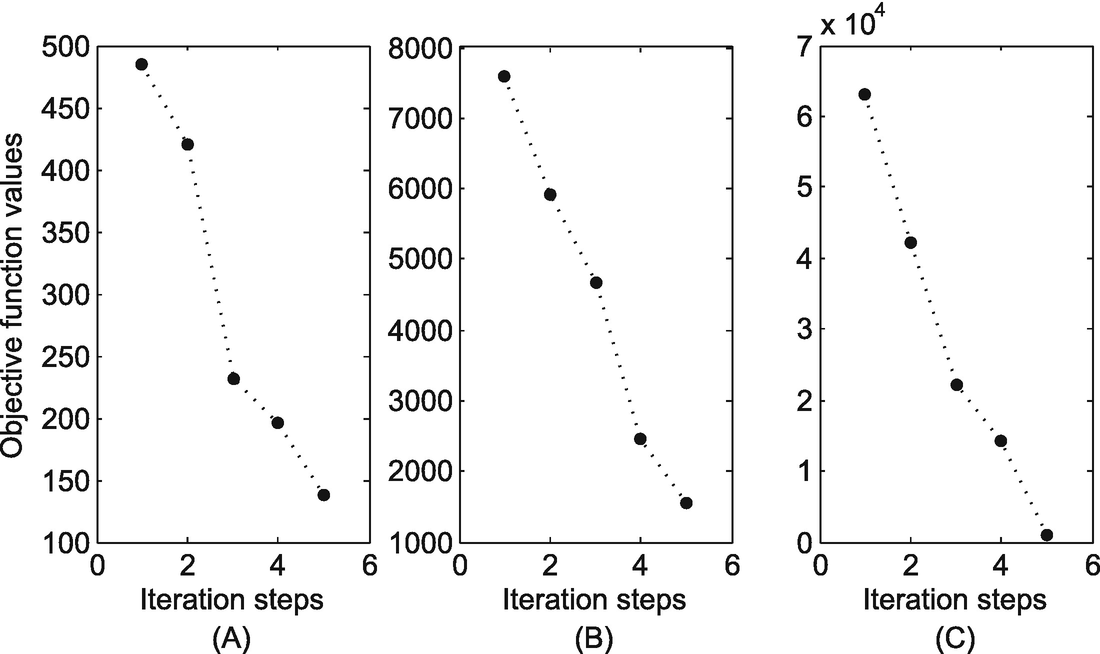
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig4_HTML.png
Fig. 11.4

The monotonically decreasing of the objective functions. (a) Power grid; (b) Yeast; (c) Facebook

11.5.1 Accuracy of Identifying Rumor Sources

We compare the performance of the proposed K-center method with two competing methods: the dynamic age method [58] and the multi-rumor-center method [115]. To quantify the performance of each method, we firstly match the estimated sources $$\hat {S} = \{\hat {s}_1, \ldots , \hat {s}_k\}$$ with the real sources S ∗ = {s 1, …, s k} so that the sum of the error distances between each estimated source and its match is minimized [160]. The average error distance is then given by
$$\displaystyle \begin{aligned} \Delta = \frac{1}{|S^*|}\sum_{i=1}^{|S^*|}h(s_i,\hat{s}_i). \end{aligned} $$
(11.20)
We expect that our method can accurately capture the real sources or at least a set of sources very close to the real sources (i.e., Δ is as small as possible).
The average error distances for the three real network topologies are provided in Table 11.2. From this table we can see that the proposed method outperforms the other two methods, that the estimated sources are closer to the real sources. To have a clearer comparison between our proposed method and the other two methods, we show the histogram of the average error distances (Δ) in Figs. 11.5 and 11.6, when |S ∗| = 2 or 3, respectively. We can see that the proposed K-center method outperforms the others. When |S ∗| = 2, the estimated sources are very close to the real sources in the Power Grid, with the average error distances are generally 1–2 hops. However, the average error distances are around 3–4 hops when using the multi-rumor-center method, and around 3–5 hops when using the dynamic age method. For the Yeast network, the diffusion sources estimated by the proposed method are with an average of 2–3 hops away from the real sources. However, the sources estimated by using the multi-rumor-center method are averagely 2–4 hops away from the real sources, and averagely 3–4 hops away when using the dynamic age method. For the Facebook network, the proposed method can estimate the diffusion sources with an average of 2–3 hops away from the real sources. However, the estimated sources are averagely 3–4 hops away from the real sources when using the other two methods. Similarly, when |S ∗| = 3, the diffusion sources estimated by the proposed method are much closer to the real sources in these real networks.
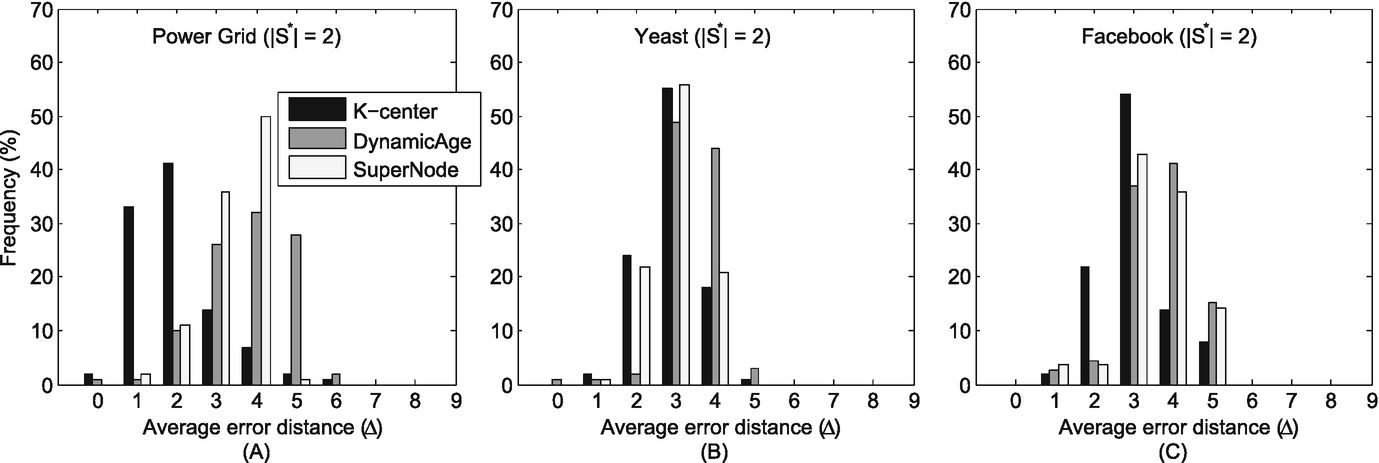
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig5_HTML.png
Fig. 11.5

Histogram of the average error distances (Δ) in various networks when S ∗ = 2. (a) Power grid; (b) Yeast; (c) Facebook

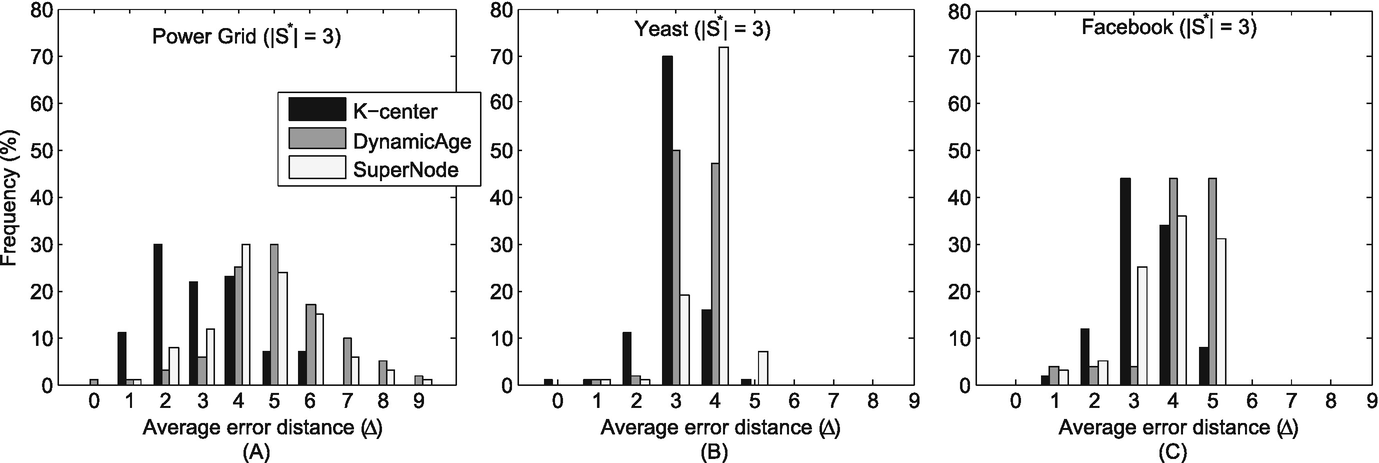
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig6_HTML.png
Fig. 11.6

Histogram of the average error distances (Δ) in various networks when S ∗ = 3. (a) Power grid; (b) Yeast; (c) Facebook

Table 11.2

Accuracy of multi-source identification

Experiment settings

Average error distance Δ

Infection percentage %

Network

|S ∗|

MRC

Dynamic age

K-center

 

Power grid

2

3.135

3.610

1.750

96.290

 

3

4.246

4.726

2.670

83.237

 

4

5.331

6.027

3.240

78.322

 

5

6.388

7.117

3.418

72.903

Yeast

2

2.700

3.175

2.680

89.606

 

3

3.520

3.146

2.733

74.762

 

4

3.525

3.077

2.962

70.599

 

5

3.474

3.050

2.874

68.563

Facebook

2

3.433

3.950

3.215

81.776

 

3

4.667

4.763

4.073

76.654

 

4

5.120

5.762

4.137

69.762

 

5

5.832

6.701

4.290

63.723

We have compared the performance of our method with two competeting methods. From the experiment results (Figs. 11.5 and 11.6, and Table 11.2), we see that our proposed method is superior to previous work. Around 80% of all experiment runs identify the nodes averagely 2–3 hops away from the real sources when there are two diffusion sources. Moreover, when there are three diffusion sources, there are also around 80% of all experiment runs identifying the nodes averagely 3 hops away from the real sources.

11.5.2 Estimation of Source Number and Spreading Time

In this subsection, we evaluate the performance of the proposed method in estimating the number of sources and predicting diffusion spreading time.

Table 11.3 shows the means and the standard deviations of the time estimation in the three real networks when we vary the real spreading time T from 4 to 6 and the number of sources |S ∗| from 2 to 3. Notice that the means of the estimated time are very close to the real spreading time under different experiment settings, and most results of the standard deviations are smaller than 1. This indicates that our method can estimate the real spreading time with high accuracy.
Table 11.3

Accuracy of spreading time estimation

Experiment settings

Estimated spreading time

Network

|S ∗|

T = 4

T = 5

T = 6

Power grid

2

4.020 ± 0.910

5.050 ± 1.256

5.627 ± 1.212

 

3

4.085 ± 0.805

5.051 ± 0.934

6.006 ± 1.123

Yeast

2

4.600 ± 0.710

5.130 ± 0.469

5.494 ± 0.578

 

3

4.534 ± 0.427

5.050 ± 0.408

5.447 ± 0.396

Facebook

2

4.380 ± 1.170

5.246 ± 0.517

5.853 ± 0.645

 

3

4.417 ± 0.736

5.378 ± 0.645

5.738 ± 0.467

Figure 11.7 shows the results in estimating the number of diffusion sources in different networks. We let the number of sources, |S ∗|, range from 1 to 3. In Fig. 11.7, the horizontal axis indicates the estimated number of sources and the vertical axis indicates the percentage of experiment runs estimating the corresponding the number sources. For the Yeast network, we see that 70% experiment runs can accurately estimate the number of sources when |S ∗| = 1. More than 80% of experiment runs can accurately estimate the number of sources when |S ∗| = 2, and around 60% when |S ∗| = 3. For the Power Grid network, it can be seen that around 50% of the total experiment runs can accurately detect the number of sources when |S ∗| ranges from 1 to 3. The accuracy is about 68% on Facebook when |S ∗| ranges from 1 to 3.
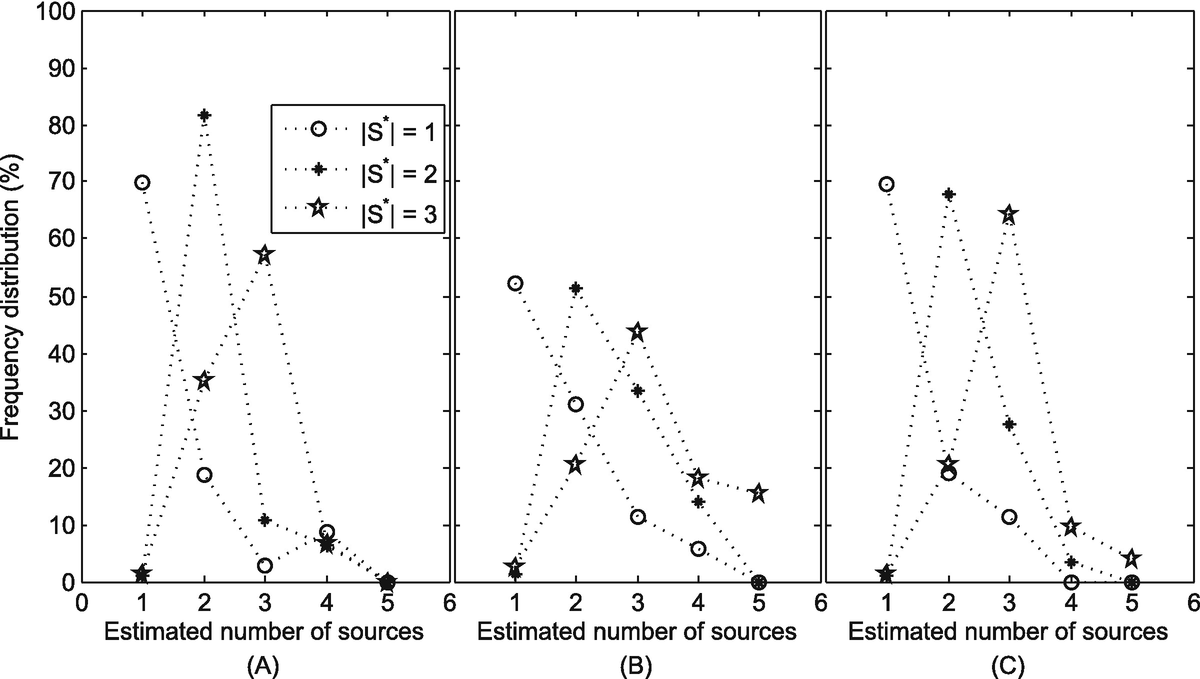
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig7_HTML.png
Fig. 11.7

Estimate of the number of sources. (a) Yeast; (b) Power grid; (c) Facebook

The high accuracy in estimating both the spreading time and the number of diffusion sources reflects the efficiency of our method from different angles.

11.5.3 Effectiveness Justification

We justify the effectiveness of the proposed K-center method from two different aspects. Firstly, we examine the correlation between the objective function values in Eq. (11.6) of the estimated sources and those of the real sources. If they are highly correlated with each other, the objective function in Eq. (11.6) will accurately describe the multi-source identification problem. Secondly, at each time tick, we examine the average effective distances from the newly infected nodes to their corresponding diffusion sources. The linear correlation between the average effective distances and the spreading time will justify the effectiveness of using effective distance in estimating multiple diffusion sources.

11.5.3.1 Correlation Between Real Sources and Estimated Sources

We investigate the correlation between the estimated sources and the real sources by examining the correlation of their objective function values in Eq. (11.6). If the estimated sources are exactly the real sources, their objective function values f should present high correlations.

Figures 11.8 and 11.9 shows the correlation results of the objective function values when |S ∗| is 2 or 3, respectively. We can see that their objective function values approximately form linear relationships. This means that the real sources and the estimated sources are highly correlated with each other. The worst results occur in Figs. 11.8a and 11.9a in the Power Grid network. However, the majority of the correlation results in these two figures still tend to be clustered in a line. The strong correlation between the real sources and estimated sources reflects the effectiveness of the proposed method.
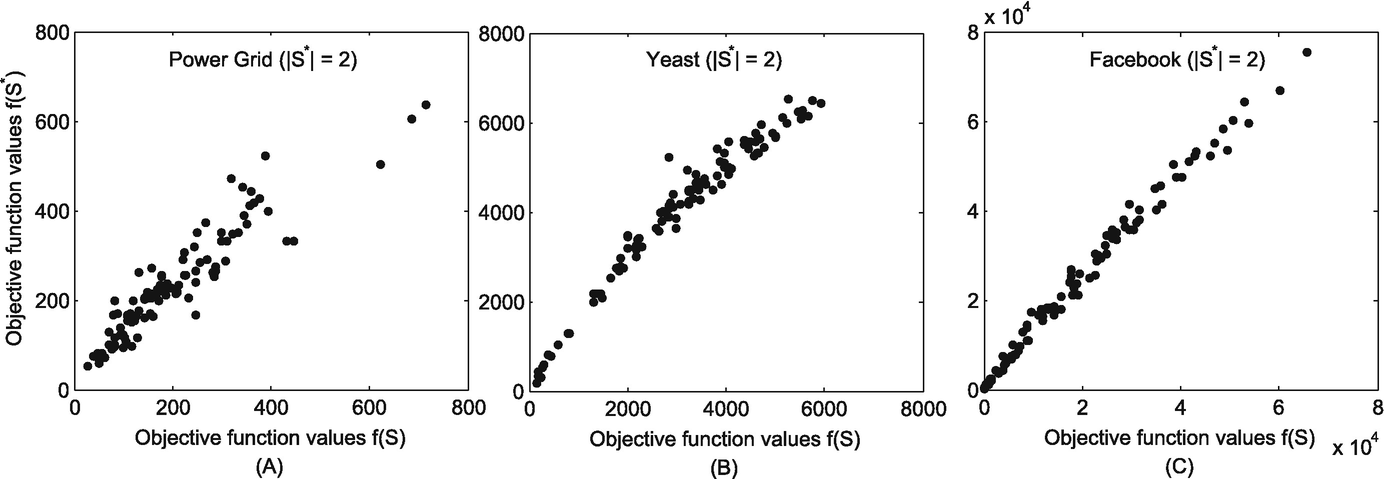
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig8_HTML.png
Fig. 11.8

The correlation between the objective function of the estimated sources and that of the real sources when S ∗ = 2. (a) Power grid; (b) Yeast; (c) Facebook

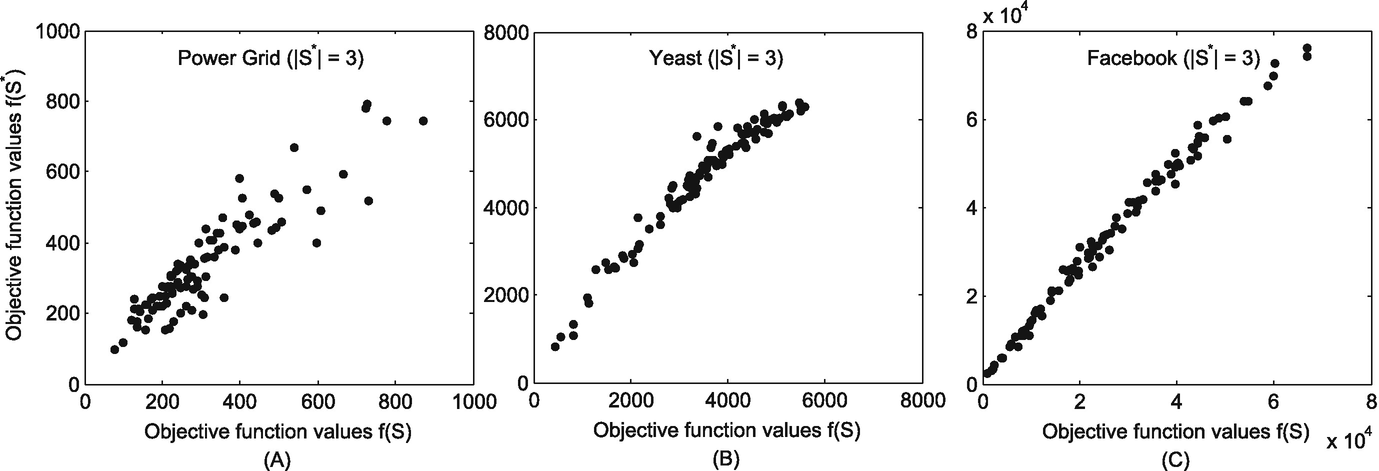
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig9_HTML.png
Fig. 11.9

The correlation between the objective function of the estimated sources and that of the real sources when S ∗ = 3. (a) Power grid; (b) Yeast; (c) Facebook

11.5.3.2 Average Effective Distance at Each Time Tick

We further investigate the correlation between the relative arrival time of nodes getting infected and the average effective distance from them to their corresponding sources. The experiment results in different networks when |S ∗| is 2 or 3 are shown in Figs. 11.10 and 11.11, respectively.
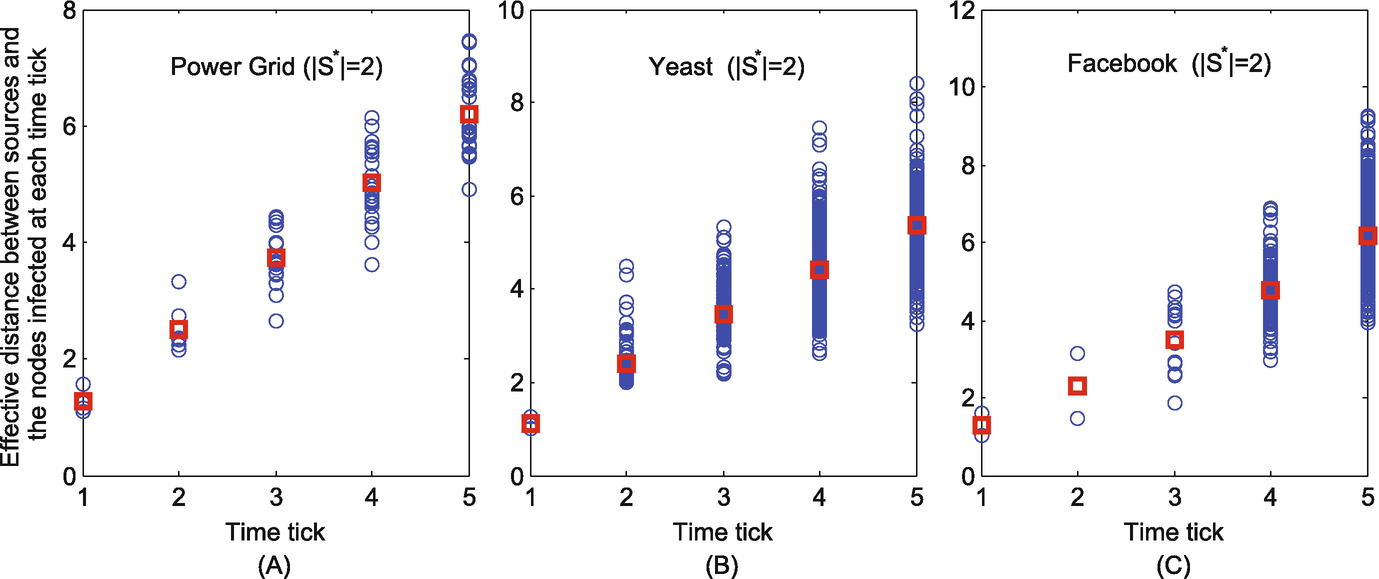
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig10_HTML.png
Fig. 11.10

The effective distances between the nodes infected at each time tick and their corresponding sources when S ∗ = 2. (a) Power grid; (b) Yeast; (c) Facebook

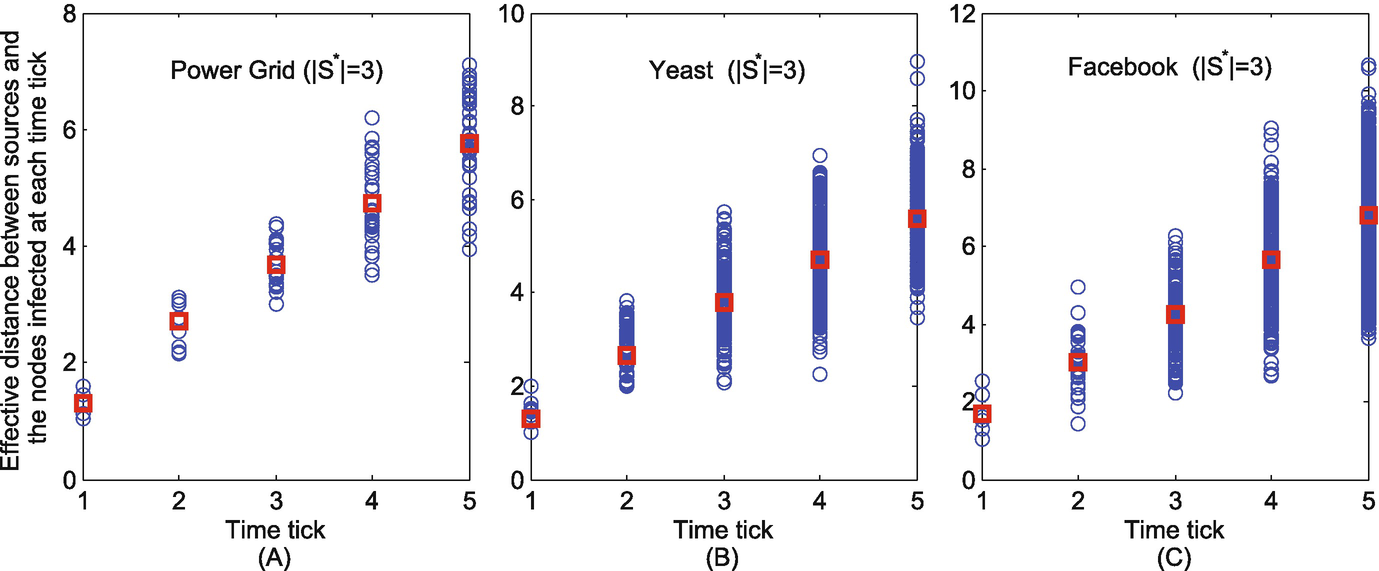
../images/466717_1_En_11_Chapter/466717_1_En_11_Fig11_HTML.png
Fig. 11.11

The effective distances between the nodes infected at each time tick and their corresponding sources when S ∗ = 3. (a) Power grid; (b) Yeast; (c) Facebook

As shown in Figs. 11.10 and 11.11, at each time tick, the effective distance from the nodes infected at this time tick to their corresponding sources are indicated as blue circles. Their average effective distance to the corresponding sources at each time tick is indicated as red square. It can be seen that the average effective distance is linear with the relative arrival time. This therefore justifies that the proposed K-center method is well-developed.

11.6 Summary

In this chapter, we studied the problem of identifying multiple rumor sources in complex networks. Few of current techniques can detect multiple sources in complex networks. We used effective distance to transform the original network in order to have a clear understanding of the complex diffusion pattern. Based on the altered network, we derive a succinct formulation for the problem of identifying multiple rumor sources. Then we proposed a novel method that can detect the positions of the multiple rumor sources, estimate the number of sources, and predict the spreading time of the diffusion. Experiment results in various real network topologies show the outperformance of the proposed method than other competing methods, which justify the effectiveness and efficiency of our method.

The identification of multiple rumor sources is a significant but difficult task. In this chapter, we have adopted the SI model with the knowledge of which nodes are infected and their connections. There are also some other models, such as the SIS and SIR. These models may conceal the infection history of the nodes that have been recovered. Therefore, the proposed method requiring a complete observation of network will not work in the SIS or SIR model. According to our study, we may need other techniques, e.g., the network completion, to cope with the SIS and SIR models. Future research includes the use of different models. Moreover, in the real world, we may only obtain partial observations of a network. Thus, future work includes multi-source identification with partial observations. We may also need to take community structures into account to more accurately identify multiple diffusion sources.