CHAPTER 17
Principles of Evidence-based Dermatology
Michael Bigby1 and Hywel C. Williams2
1Harvard Medical School and Beth Israel Deaconess Medical Center, Boston, MA, USA
2Centre of Evidence-Based Dermatology, Nottingham University Hospitals NHS Trust, Nottingham, UK
Evidence-based medicine
What is evidence-based medicine?
Evidence-based medicine (EBM) is the integration of best research evidence with clinical expertise and patient values. When these three elements are integrated, clinicians and patients form a diagnostic and therapeutic alliance which optimizes clinical outcomes and quality of life. (http://www.oucom.ohiou.edu/ebm/def.htm; last accessed May 2014)
The need for evidence-based medicine
Distinguishing effective treatments from those that are ineffective or harmful
Distinguishing effective treatments from those that are ineffective or harmful has been a problem facing medical practitioners since medicine has been practised [1]. Prior to the 1940s, determination of treatment efficacy was based on expert opinion, trial and error, uncontrolled observation and small case series. The only treatments that could be distinguished as effective were those that produced dramatic increases in survival such as streptomycin for tuberculous meningitis [1]. The publication of the randomized controlled clinical trial (RCT) that demonstrated that streptomycin was effective in the treatment of pulmonary tuberculosis was a landmark event in determining treatment efficacy [2]. Since then, the RCT has become the gold standard for determining the efficacy of therapeutic interventions. Hundreds of RCTs were conducted between 1950 and 1980. However, their results were not catalogued or used systematically to inform medical decision making.
Evidence-based medicine is a framework designed to help practitioners distinguish interventions that are effective from those that are ineffective or harmful. The origin of evidence-based medicine is most often traced to Pierre Charles Alexander Louis who introduced the teaching of statistical methods into the study of medicine in post-revolutionary France. However, a strong case can be made that its modern originator was Archie Cochrane, a British epidemiologist and physician, who in 1971 published his response to being asked to evaluate the effectiveness of the British National Health Service in delivering health care to the population of the UK. In his analysis he concluded that medical science was poor at distinguishing interventions that were effective from those that were not and that physicians were not using available evidence from clinical research to inform their decision making [1, 3].
Like-minded epidemiologists and physicians responded to Archie Cochrane's challenge by examining the methods by which medical decisions and conclusions were reached and proposed an alternative method of summarizing evidence based on finding, appraising and utilizing available data from clinical research performed on patients. In 1985 Sackett, Haynes, Guyatt and Tugwell published a landmark book entitled Clinical Epidemiology: A Basic Science for Clinical Medicine that detailed the rationale and techniques of this evidence-based approach [4]. These authors and others reduced the rules of evidence to a small subset of principles that were easier to teach and to understand and reintroduced the concept in 1992. They named this technique ‘evidence-based medicine’. It was defined as ‘the conscientious, explicit and judicious use of the best current evidence in making decisions about the care of individual patients’ [5]. The definition was expanded to include the integration of independent clinical expertise, best available external clinical evidence from systematic research, and patients’ values and expectations [6]. Others like Iain Chalmers were instrumental in setting up the Cochrane Collaboration, a global network of mainly volunteers tasked with preparing and maintaining unbiased systematic reviews of all RCTs, organized according to specialty [7]. Whereas making a decision about therapy has been the primary focus of EBM, its principles have been extended to diagnosis, prognosis, harmful effects of interventions and economic analyses [1].
It has been estimated that physicians need evidence (e.g. about the accuracy of diagnostic tests, the power of prognostic markers, the comparative efficacy and safety of interventions) about twice for every three out-patients seen (and five times for every in-patient). They get less than a third of this evidence because they do not look for it, cannot find it or it does not exist [1, 8, 9].
Keeping up with the literature
The best external evidence that informs patient care comes from clinical research involving patients. It has a short doubling-time (10 years) and replaces currently accepted diagnostic tests and treatments with new ones that are more powerful, more accurate, more efficacious and safer [1].
In the field of medicine the amount of data published far exceeds our ability to read it. Keeping up by reading the literature is an impossible task for most practising physicians. It would require reading around 19 articles a day, 365 days a year. The average practising physician spends 30 min per week reading the medical literature related to the patients he or she sees (Figure 17.1) [1, 6, 8]. The burden of literature for dermatologists is no less daunting since there are now more than 200 journals devoted to dermatology worldwide [1, 10, 11]. Such expansion in the biomedical literature has been one of the main reasons for developing secondary research synthesis summaries (systematic reviews) of all available evidence, so that the busy physician can go to just one place for an up-to-date summary.
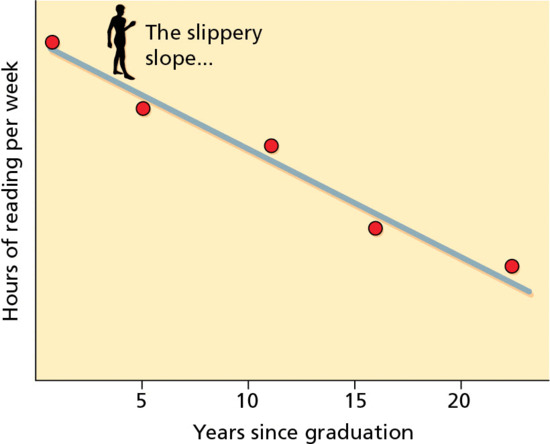
Figure 17.1 Relationship between reading and years from graduation from medical school. (Adapted from Sackett 1997 [21].
Reproduced with permission of Elsevier.)
Even if he or she had the time, the best clinical evidence published in journals is often inaccessible to the average practising physician. Most are not adequately trained in clinical decision making, clinical research, epidemiology or statistics to read many articles published in the primary medical literature. Commonly used techniques and concepts such as odds ratio, confidence interval, utility, Yates correction or fixed effects model, as examples, are inadequately understood. EBM provides a systematic method to evaluate the medical literature that allows the average practising physician to understand the medical literature and to apply it to the care of individual patients.
Practising evidence-based medicine
Practising EBM consists of five steps (Box 17.1) that are explained in detail in the following sections of this chapter. Once learned, the techniques of evidence-based medicine can be performed rapidly and efficiently to use available external evidence from the medical literature with clinical experience and patient preferences to make clinical decisions.
Limitations of evidence-based medicine
Practising EBM is limited by several inherent weaknesses predominately resulting from having to rely on evidence published in the medical literature (Box 17.2). Publication bias results from allowing factors other than quality of the research to influence its acceptability for publication (e.g. sample size, statistical significance or investigators’ or editors’ perception of whether the results are ‘interesting’) [1, 12]. There is a strong bias favouring studies with positive results even if they have methodological weaknesses and small sample size. Negative studies with small sample size are much less likely to be published. Even studies with large sample sizes and negative results may go unpublished: for example two RCTs that demonstrated that topical imiquimod was ineffective in the treatment of molluscum contagiosum have not yet been published [13].
As a result of publication bias, easy to locate studies are more likely to show ‘positive’ effects [1, 12]. In many areas, the studies published are dominated by company-sponsored trials of new, expensive treatments. Treatment is often only compared with placebo in these studies, making it difficult for practising clinicians to decide how the new treatment compares with existing therapies.
Many trials published in the dermatological literature (and in the medical literature generally) are of poor methodological quality. Surveys of clinical trials published in the dermatological literature list the features of trials most important in limiting the risk of bias (e.g. adequate randomization, concealed allocation, intention-to-treat analysis and masking). These features were reported less than 50% of the time [14, 15]. Reporting does not appear to have improved over time. In a systematic review of the treatment of pityriasis versicolor published in 2010, adequate randomization, concealed allocation, intention-to-treat analysis and masking were reported 20%, 10%, 35% and 44% of the time respectively [16].
Sufficient evidence is lacking in many areas in dermatology (and in medicine in general). An analysis of systematic reviews of dermatological topics found insufficient evidence to inform practice in 60% (63/105) [17]. Many dermatological diseases are very uncommon and have not been studied in controlled clinical trials. Case series, case reports and expert opinion based on experience are still legitimate evidence for rare skin diseases where no clinical trials or systematic reviews are available.
‘All or none’ clinical observations such as the use of streptomycin for tuberculous meningitis and insulin for diabetes provide strong evidence of treatment efficacy and obviate the need for expensive and time-consuming clinical trials. The use of dapsone for dermatitis herpetiformis and systemic corticosteroids for pemphigus vulgaris may serve as examples of ‘all or none’ clinical observations in dermatology.
Results in published clinical trials are almost always expressed in summary statistics that refer to the groups treated in the study. Summary statistics refer to groups not individuals (e.g. PASI-75 (psoriasis area and severity index) or proportions who cleared). Some participants may respond a lot and others very little, whereas only the average response is reported. Ideally, in addition to group data, the raw data of individual treatment responses should be presented or made available to determine whether it is possible to identify factors that make it more or less likely that a patient will respond to treatment. These data are rarely provided. Unfortunately in dermatology, most trials are relatively small and of short duration. As a result, they are underpowered to identify predictors of response that could help to identify those groups of people who might respond better or worse to a particular treatment.
Threats to evidence-based medicine
The practice of EBM faces threats from several entities that seek to exploit it for gain (Box 17.3). Some authors approach systematic reviews and meta-analyses as a quick way to get published. A common practice is to look into the literature for areas in which many trials have been published and write a data-driven systematic review. These reviews tend to include many company-sponsored trials of new and expensive treatments compared with placebo which do not necessarily address important clinical questions raised in clinical practice.
Many published therapeutic trials are company-sponsored trials of new treatments. These trials are more likely to have results favourable to the sponsor [18]. Compared with trials funded by other sources, company-sponsored trials that are pre-registered with government registration sites (e.g. trials.gov and clinicaltrialsregister.eu; both last accessed May 2014) are less likely to be published, perhaps indicating that trials with negative results are intentionally not finished or published [18].
Trials with negative results for the primary outcome are often ‘spun’ to give the appearance that the treatment is effective. This objective is accomplished by de-emphasizing the primary outcome and selectively reporting or emphasizing results in secondary outcomes, subgroup analyses or post hoc analyses. In a representative sample of RCTs published in 2006 with statistically non-significant primary outcomes, the reporting and interpretation of findings was frequently inconsistent with the results [19]. Selective outcome reporting bias can be partially overcome by systematic reviews stipulating the preferred clinically important outcomes and by those conducting clinical trials to register their protocol and to state their primary outcome measures of success in publicly accessible trial registers before recruitment starts [20].
Formulating questions and finding evidence
Formulating well-built clinical questions
Practising EBM centres on trying to find answers to clinically relevant questions that arise in caring for individual patients. Asking well-built clinical questions may be the most important step in practising EBM [1]. A well-built clinical question has four elements: a patient or problem, an intervention, a comparison intervention (if necessary) and an outcome. One easy way of remembering these key components is the acronym PICO (patient, intervention, comparator and outcome). A fifth element, time frame (i.e. the time it takes for the intervention to achieve the outcome or how long participants in a study are observed), has been suggested as an additional component for the well-built clinical question yielding the acronym PICOT (Figure 17.2) [2, 3].

Figure 17.2 The PICOT format.
Well-built clinical questions about individual patients can be grouped into several categories: aetiology, diagnosis, therapy, prevention, prognosis and harm. An example of a well-built question about diagnosis is ‘In patients with dystrophic toenails due to onychomycosis [P], would a fungal culture [I] or a periodic acid–Schiff stain (PAS) of a nail clipping [C] be more likely to establish a diagnosis of onychomycosis [O]?’ An example of a well-built question about therapy is ‘In immunocompetent children with cutaneous warts [P], would treatment with imiquimod [I] or vehicle [C] result in clearance of all lesions [O] after 2 months of treatment [T]?’ An example of a well-built question about harm is ‘What is the likelihood that a patient with severe nodular acne [P] treated with isotretinoin [I] or not exposed to isotretinoin [C] will develop ulcerative colitis [O] within 12 months after completing a course of treatment [T]?’
A well-formed clinical question has two strong advantages. Firstly, a major benefit of careful and thoughtful question forming is that it makes the search for, and the critical appraisal of, the evidence easier. The well-formed question makes it relatively straightforward to elicit and combine the appropriate terms needed to tailor the search strategies for the database(s) you choose (e.g. MEDLINE, EMBASE, Cochrane Library). Secondly, having to formulate well-built clinical questions will also train you to define your patient clearly, be specific about the interventions used and choose carefully the outcomes that would make a difference to your patient and you.
What is ‘the best evidence’?
Practising EBM is predicated on finding and utilizing the best evidence [4]. Potential sources of evidence include empirical reasoning based on the aetiology and pathophysiology of disease, personal experience, colleagues or experts, textbooks, articles published in journals, and systematic reviews and guidelines. An important principle of EBM is that the quality (strength) of evidence is based on a hierarchy of evidence (Figure 17.3). The order of the hierarchy of evidence is dependent on the type of question being asked (Table 17.1). The hierarchy of evidence consists of results of well-designed experimental studies such as RCTs (especially if the studies have results of similar magnitude and direction, and if there is homogeneity among studies), results of observational studies such as case series, expert opinion and personal experience, in descending order. The hierarchy was created to encourage the use of the evidence that is most likely to be true and useful in clinical decision making. The ordering of this hierarchy has been widely discussed, actively debated and sometimes hotly contested [5]. It is important to consider study quality when referring to the evidence hierarchy. For example, a well-designed cohort study may provide more reliable evidence than a small, poorly conducted RCT (even though the RCT hypothetically offers a stronger design for minimizing bias).
Table 17.1 Levels of evidence.
| Level of evidence | Therapy/harm | Diagnosis |
| 1a | Multiple randomized controlled trials (RCTs) with homogeneitya | Multiple level 1b (see 1b entry) diagnostic studies with homogeneity; or clinical decision rulesb with 1b studies from different clinical centres |
| 1b | Individual RCT (with narrow confidence intervals) | Independent blind comparison of an appropriate spectrum of consecutive patients, all of who have undergone both the diagnostic test and the reference standard |
| 1c | All or nonec | Very high sensitivity or specificityd |
| 2a | Cohort studies with homogeneity | Multiple level ≥2 (see entries below) diagnostic studies with homogeneity |
| 2b | Individual cohort study (including low-quality RCT; e.g. <80% follow-up) | Independent blind comparison but either in non-consecutive patients, or confined to a narrow spectrum of study individuals (or both), all of whom have undergone both the diagnostic test and the reference standard; or a diagnostic clinical decision rule (CDR) not validated in a test set |
| 2c | ‘Outcomes’ researche | |
| 3a | Case–control studies with homogeneity | Multiple level 3b and better studies (see below) with homogeneity. |
| 3b | Individual case–control study | Independent blind comparison of an appropriate spectrum, but the reference standard was not applied to all study patients |
| 4 | Case series (and poor quality cohort and case–control studies) | Reference standard was not applied independently or not applied blindly |
| 5 | Expert opinion without explicit critical appraisal, or based on physiology, bench research or logical deduction |
Adapted from NHS R&D Centre for Evidence-Based Medicine (http://www.cebm.net/index.aspx?o=1025; last accessed May 2014).
aHomogeneity means lacking variation in the direction and magnitude of results of individual studies.
bClinical decision rules are algorithms or scoring systems that lead to a prognostic estimation or a diagnostic category.
cAll or none – these are interventions that produced dramatic increases in survival or outcome such as streptomycin for tuberculous meningitis.
dA diagnostic finding whose specificity is so high that a positive result rules in the diagnosis or a diagnostic finding whose sensitivity is so high that a negative result rules out the diagnosis.
eOutcomes research includes cost-benefit, cost-effectiveness and cost-utility analysis.

Figure 17.3 The hierarchy of evidence.
A systematic review is an overview of available evidence that answers a specific clinical question, contains a thorough, unbiased search of the relevant literature, explicit criteria for assessing studies and structured presentation of the results. When there are similar studies in a systematic review (i.e. RCTs using the same interventions and outcomes), the authors of a systematic review may use a statistical technique called meta-analysis to combine quantitative data from several studies in order to provide a more precise and informative overall estimate of treatment effects.
Meta-analysis is credited with allowing recognition of important treatment effects by combining the results of small trials that individually lacked the power to demonstrate differences among treatments. For example, the benefits of intravenous streptokinase in acute myocardial infarction was recognized by the results of a cumulative meta-analysis of smaller trials at least a decade before it was recommended by experts and before it was demonstrated to be efficacious in large clinical trials [6]. Meta-analysis has been criticized for the discrepancies between the results of meta-analysis and the results of large clinical trials [7]. For example, results of a meta-analysis of 14 small studies of calcium to treat pre-eclampsia showed benefit of treatment, whereas a large trial failed to show a treatment effect [8]. The frequency of discrepancies ranges from 10% to 23% [8]. Discrepancies can often be explained by differences in treatment protocols, heterogeneity of study populations or changes that occur over time [8].
The type of question being asked determines the type of clinical study that constitutes the best evidence. Questions about therapy and interventions for disease prevention are best addressed by RCTs. Questions about diagnosis are best addressed by cohort studies. RCTs are usually a good source of evidence for the harmful effects of interventions for adverse events that occur frequently, but not for rare but potentially important adverse events. For adverse effects that occur infrequently, cohort studies, case–control studies or post-marketing surveillance studies are best. Case reports are often the first line of evidence for very rare adverse events and sometimes they are the only evidence.
Over three-quarters of a million RCTs have been conducted in medicine. Studies have demonstrated that failure to use randomization or adequate concealment of allocation results in larger estimates of treatment effects, predominantly caused by a poorer prognosis in non-randomly selected control groups compared with randomly selected control groups [9]. However, studies comparing randomized and non-randomized clinical trials of the same interventions have reached disparate and controversial results [10, 11]. Some found that observational studies find stronger treatment effects than randomized controlled trials [9]. Others found that the results of well-designed observational studies (with either a cohort or case–control design) do not systematically overestimate the magnitude of the effects of treatment as compared with RCTs on the same topic [10, 11]. Sifting through the controversy leads to the following limited conclusions: trials using historical controls result in larger estimates of treatment effects compared with randomized controlled trials. Large, inclusive, fully masked controlled trials that generate and conceal the randomization sequence properly and include all those who are originally allocated to the treatment groups (intention-to-treat analysis) are likely to provide the best evidence about effectiveness [5]. RCTs and systematic reviews of well-designed clinical studies have informed the care of dermatological patients [12].
Whereas personal experience is an invaluable part of becoming a competent physician, the pitfalls of relying too heavily on personal experience have been widely documented. Nisbett and Ross extensively reviewed people's ability to draw inferences from personal experience and document several pitfalls [13]. They include:
- Overemphasis on vivid, anecdotal occurrences and underemphasis on significant statistically strong evidence.
- Bias in recognizing, remembering and recalling evidence that supports pre-existing knowledge structures (e.g. ideas about disease aetiology and pathogenesis) and parallel failure to recognize, remember and recall evidence that is more valid.
- Failure to characterize population data accurately because of ignorance of statistical principles including sample size, sample selection bias and regression to the mean.
- Inability to detect and distinguish statistical association and causality.
- Persistence of beliefs in spite of overwhelming contrary evidence.
Nisbett and Ross provide numerous examples of problems associated with recall from controlled clinical research. Physicians may remember patients who improved, often assume that patients who did not return for follow-up improved and conveniently forget the patients who did not improve. A patient treated with a given medication may develop a severe life-threatening reaction. On the basis of this single undesirable experience, the physician may avoid using that medication for many future patients, even though, on average, it may be more efficacious and less toxic than the alternative treatments that the physician chooses.
Few physicians keep adequate, easily retrievable records to codify results of treatments with a particular agent or of a particular disease; and even fewer actually carry out analyses. Few physicians make provisions for tracking those patients who are lost to follow-up. Therefore, statements made about a physician's ‘clinical experience’ may be biased. Finally, for many conditions, a single physician sees far too few patients to enable reasonably firm conclusions to be drawn about the response to treatments. For example, suppose a physician treated 20 patients with lichen planus with tretinoin and found that 12 (60%) had an excellent response. The confidence interval for this response rate (i.e. the true response rate for this treatment in the larger population from which this physician's sample was obtained) ranges from 36% to 81% (http://statpages.org/confint.html; last accessed May 2014). Thus the true overall response rate might well be substantially less (or more) than the physician concludes from personal experience.
Expert opinion can be valuable, particularly for rare conditions in which the expert has the most experience, or when other forms of evidence are not available. However, several studies have demonstrated that expert opinion often lags significantly behind conclusive evidence. Experts may rely too heavily on bench research, pathophysiology and treatments based on logical deduction from pathophysiology, and from the same pitfalls noted for relying on personal experience.
It is widely believed that clinical decisions can be made on the basis of understanding the aetiology and pathophysiology of disease and logic [14]. This paradigm is problematic since the accepted hypothesis for the aetiology and pathogenesis of disease changes over time. For example, in the last 20 years, hypotheses about the aetiology of psoriasis have shifted from a disorder of keratinocyte proliferation and homeostasis, to abnormal signalling of cyclic adenosine monophosphate, to aberrant arachidonic acid metabolism, to aberrant vitamin D metabolism, to the current favourite, a T-cell-mediated autoimmune disease. Each of these hypotheses spawned logically deduced treatments. The efficacy of many of these treatments has been substantiated by rigorous controlled clinical trials, whereas others are used even in the absence of systematically collected observations. Therefore, many options are available for treating patients with severe psoriasis (e.g. UVB, narrow-band UVB, the Goeckerman regimen, psoralen–UVA (PUVA), methotrexate, ciclosporin, tumour necrosis factor (TNF) inhibitors and IL-12/23 inhibitors) and mild to moderate psoriasis (e.g. anthralin, topical corticosteroids, calcipotriol and tazarotene). However, a clear sense of what is best, in what order they should be used, or in what combinations, is still lacking.
Treatments based on logical deduction from pathophysiology may have unexpected consequences. For example, it was postulated that thalidomide might be a useful treatment for toxic epidermal necrolysis, based on the observation that thalidomide showed anti-TNF-α properties. However, an RCT of thalidomide was stopped early because it was found that mortality was significantly higher in the thalidomide group than in the placebo group [15].
Textbooks can be valuable, particularly for rare conditions and for conditions for which the evidence does not change rapidly over time. However, textbooks have several well-documented shortcomings. They tend to reflect the biases and shortcomings of the authors who write them. By virtue of how they are written, produced and distributed, most are at least 2 years out of date at the time of publication. Most textbook chapters are narrative reviews that do not systematically search for all available evidence and appraise the quality of the evidence reported.
Finding the best evidence
The ability to find the best evidence to answer clinical questions is crucial for practising evidence-based medicine [2]. Finding evidence requires access to electronic searching, searching skills and available resources. Evidence about therapy is the easiest to find. The best sources for finding the best evidence about treatment include:
- The Cochrane Library.
- Searching the Medline and EMBASE databases.
- Primary journals.
- Secondary sources that summarize important new research.
- Evidence-based dermatology and evidence-based medicine books.
- The National Guideline Clearinghouse (http://www.guideline.gov; last accessed May 2014).
- The National Institute for Health and Care Excellence (NICE) (www.nice.org.uk; last accessed May 2014).
The Cochrane Collaboration formed in response to Archie Cochrane's challenge to organize a critical summary, by specialty or subspecialty, adapted periodically, of all relevant randomized controlled trials. The Cochrane Library contains the Cochrane Database of Systematic Reviews, the Database of Abstracts of Reviews of Effectiveness (DARE), the Cochrane Central Register of Controlled Trials (Central) and the Health Technology Assessment (HTA) database. The Cochrane Library is the most complete and best index database of systematic reviews of therapy, randomized controlled clinical trials and controlled clinical trials and is the best and most efficient place to find evidence about therapy.
The Cochrane Database of Systematic Reviews is the most comprehensive collection of high-quality systematic reviews available. Volunteers, according to strict guidelines developed by the Cochrane Collaboration, write the systematic reviews in the Cochrane Library. Systematic reviews conducted within the Cochrane Collaboration are rated among the best [16]. The last issue of the Cochrane Library (2014, issue 6, accessed 9 December 2014) contained 8210 completed systematic reviews. The number of reviews relevant to dermatology is more than 400 and is steadily increasing [17].
Central is a database of over 717 246 controlled clinical trials. It is compiled by searching several databases including Medline, EMBASE and Literatura Latino Americana em Ciências da Saúde (LILACS), and hand-searching many journals. Hand-searching journals to identify controlled clinical trials and RCTs was undertaken because members of the Cochrane Collaboration noticed that many published trials were incorrectly classified in the Medline database. As an example, Adetugbo et al. hand-searched the Archives of Dermatology from 1990 through 1998 and identified 99 controlled clinical trials. Nineteen of the trials were not classified as controlled clinical trials in Medline and 11 trials that were not controlled clinical trials were misclassified as controlled clinical trials in Medline [18].
DARE is a database of abstracts of systematic reviews published in the medical literature. It contains abstracts and bibliographic details on over 26 293 published systematic reviews. DARE is the only database to contain abstracts of systematic reviews that have been quality assessed. Each abstract includes a summary of the review together with a critical commentary about the overall quality. HTA consists of completed and ongoing health technology assessments (studies of the medical, social, ethical and economic implications of health care interventions) from around the world. The aim of the database is to improve the quality and cost-effectiveness of health care.
The Cochrane Library is the best source for evidence about treatment. It can be easily searched using simple Boolean combinations of search terms and by more sophisticated search strategies. The Cochrane Database of Systematic Reviews, DARE, Central and HTA can be searched simultaneously. The Cochrane Library is available on a personal or institutional subscription basis on CD, and on the World Wide Web from the Cochrane Collaboration (http://www.thecochranelibrary.com/view/0/index.html; last accessed May 2014). Subscriptions to the Cochrane Library are updated quarterly. The Cochrane Library is offered free of charge in many countries such as the UK by national provision, and to faculty and students by many medical schools in the USA. It is also available free to those in developing countries through a program called Health InterNetwork Access to Research Initiative (HINARI).
The second best method for finding evidence about treatment and the best source for finding most other types of best evidence in dermatology is by searching the Medline or EMBASE databases by computer. MEDLINE is the National Library of Medicine's bibliographic database covering the fields of medicine, nursing, dentistry, veterinary medicine, the health care system and the pre-clinical sciences. The MEDLINE file contains bibliographic citations and author abstracts from approximately 5600 current biomedical journals published in the USA and 80 other countries. The file contains approximately 19 million records dating back to 1948.
Medline searches have inherent limitations that make their reliability less than ideal [4]. For example, Spuls et al. conducted a systematic review of systemic treatments of psoriasis [19]. Treatments analysed included UVB, PUVA, methotrexate, ciclosporin and retinoids. The authors used an exhaustive strategy to find relevant references including Medline searches, contacting pharmaceutical companies, polling leading authorities, reviewing abstract books of symposia and congresses, and reviewing textbooks, reviews, editorials, guideline articles and the reference lists of all papers identified. Of 665 studies found, 356 (54%) were identified by Medline search (range 30–70% for different treatment modalities). The 17 of 23 authorities who responded provided no references beyond those identified by Medline searching.
Specific search strategies, ‘filters’, have been developed to help find relevant references and exclude irrelevant references for systematic reviews, and for the best evidence about aetiology, diagnosis, therapy and prevention, prognosis and clinical prediction guides (http://www.ncbi.nlm.nih.gov/books/NBK3827/#pubmedhelp.Clinical_Queries_Filters; last accessed May 2014). These filters have been incorporated into the PubMed Clinical Queries search engine of the National Library of Medicine and are available at http://www.ncbi.nlm.nih.gov/pubmed/clinical (last accessed May 2014). PubMed Clinical Queries is the preferred method for searching the Medline database for the best, clinically relevant evidence. It can be freely used by anyone with internet access.
EMBASE is Elsevier's database covering drugs, pharmacology and biomedical specialties. EMBASE contains bibliographic citations and author abstracts from approximately 8300 current biomedical journals published in 90 countries, with a focus on drugs and pharmacology, medical devices, clinical medicine and basic science relevant to clinical medicine. The file contains over 28 million records dating back to 1947. EMBASE has a better coverage of European and non-English language sources and may be more up to date than Medline [20]. EMBASE includes all 19+ million records indexed by Medline. EMBASE is available online (http://www.elsevier.com/online-tools/embase; last accessed May 2014). Personal and institutional subscriptions are available. EMBASE performs simultaneous searches of EMBASE and Medline databases and eliminates duplicate records.
Clinicians are increasingly using general internet search engines such as Google and Google Scholar to search for medical evidence. In a comparison of searches in three areas in respiratory medicine, PubMed Clinical Queries had better precision (positive predictive value) than Google Scholar for both overall search results (13% versus 0.07%, P <0.001) and full-text results (8% versus 0.05%, P <0.001). PubMed Clinical Queries and Google Scholar had similar recall (sensitivity) for both overall search results (71% versus 69%) and full-text results (43% versus 51%) [21]. In contrast to Clinical Queries searches, general searches of Medline are not consistently better than Google Scholar searches and are considerably worse in some studies [22, 23].
The National Guideline Clearinghouse maintains a database of guidelines for the treatment of disease written by panels of experts following strict guidelines of evidence. The database is accessible through the internet (http://www.guideline.gov/; last accessed May 2014). The current coverage of dermatological topics is limited.
The UK NICE produces guidance on public health, health technologies and clinical practice based on the best available evidence. It is accessible online at www.nice.org.uk (last accesssed May 2014) and includes guidance for treating atopic eczema in children, a final appraisal determination on the use of calcineurin inhibitors for atopic eczema, and on the use of biologicals for psoriasis and alitretinoin for hand eczema, and a full set of guidelines for skin cancer including melanoma.
Other secondary sources of evidence exist such as those produced by the Centre of Evidence Based Dermatology http://www.nottingham.ac.uk/research/groups/cebd/resources/index.aspx (last accessed May 2014), which includes annual evidence updates on eczema and acne, and the Global Resource for all RCTs Conducted on Atopic Eczema (GREAT) [24].
Critically appraising evidence and applying it to individual patients
Critically appraising the evidence
After finding evidence, the next step in practising EBM involves critically appraising the evidence [1, 2]. Key questions that can be used to critically appraise systematic reviews and papers about treatment, diagnostic tests and harmful effects of exposures are described in Boxes 17.4, 17.5, 17.6 and 17.7. Papers that meet these criteria are more likely to provide information that is true and useful in the care of patients. Detailed explanation of each criterion and examples using a patient with a dermatological complaint are available [1].
Critically appraising evidence consists of three steps to determine whether the results are:
- Valid (i.e. as unbiased as possible).
- Clinically important.
- Applicable to the specific patient being seen.
Determining the validity of evidence centres on ascertaining whether the evidence was produced in a manner most likely to eliminate and avoid bias. Clinical importance is determined by looking at the magnitude of the effect of the intervention (e.g. response difference and number needed to treat for therapy, likelihood ratio for diagnostic studies and relative risk, odds ratios or number needed to harm for studies of harm) and its corresponding precision (usually expressed as the 95% confidence interval). To determine whether the evidence is applicable to a specific patient requires physician expertise, knowledge of the patient's preferences and an evaluation of the availability, risks and benefits of the intervention.
Critically appraising systematic reviews
Not all systematic reviews and meta-analyses are equal. A systematic review should be conducted in a manner that will include all of the relevant trials, minimize the introduction of bias, and synthesize the results to be as truthful and useful to clinicians as possible [1, 2]. Criteria for reporting systematic reviews were developed by a consensus panel first published as Quality of Reporting of Meta-analyses (QUOROM) and later refined as Preferred Reporting Items for Systematic Reviews and Meta-analyses (PRISMA). This detailed, 27-item checklist contains the items that should be included and reported in high-quality systematic reviews and meta-analyses [3].
All systematic reviews should follow a planned protocol that should be published in the public domain before the review is carried out in order to avoid duplication of effort and in order to minimize selective outcome reporting bias (i.e. emphasizing the outcomes that turn out to be statistically significant). The international Prospective Register of Systematic Reviews (PROSPERO) now exists for this purpose (http://www.crd.york.ac.uk/PROSPERO/; last accessed May 2014).
Are the results of the systematic review valid?
The items that strengthen the validity of a systematic review include having clear objectives, explicit criteria for study selection, an explicit and thorough search of the literature, an assessment of the quality of included studies, criteria for which studies can be combined, and appropriate analysis and presentation of results (Box 17.4). Meta-analysis is only appropriate if the included studies are conceptually similar. Meta-analyses should be conducted only within the context of a systematic review [1, 4].
A systematic review should have clear, focused clinical objectives. Like the well-built clinical question for individual studies, a focused clinical question for a systematic review should contain four elements: (i) a patient, group of patients or problem; (ii) an intervention; (iii) comparison intervention(s); and (iv) specific outcomes. The patient populations should be similar to patients seen in the population to which one wishes to apply the results of the systematic review. The interventions studied should be those commonly available in practice. Outcomes reported should be those that are most relevant to physicians and patients.
A sound systematic review can be performed only if most or all of the available data are examined. An explicit and thorough search of the literature should be performed. It should include searching several electronic bibliographic databases including the Cochrane Controlled Trials Registry (CCTR), Medline, EMBASE and LILACS. Bibliographies of retrieved studies, review articles and textbooks should be examined further for studies fitting the inclusion criteria. There should be no language restrictions. Additional sources of data include scrutiny of citation lists in retrieved articles, hand-searching for conference reports, prospective trial registers (e.g. http://clinicaltrials.gov for the USA and www.clinicaltrialsregister.eu for the European union; both last accessed May 2014) and contacting key researchers, authors and drug companies [1, 5].
The overwhelming majority of systematic reviews involve therapy. Because of their ability to minimize bias, RCTs should be used as the preferred study design for inclusion in systematic reviews of therapy if they are available. The criteria commonly used to assess the quality of included trials are described in the Cochrane Collaboration risk of bias tool and include: concealed, random allocation, groups similar in terms of known prognostic factors, equal treatment of groups, masked (also known as blinded) evaluation of treatment outcomes and accounting for all patients entered into the trial in analysing results (intention-to-treat design) [6, 7].
Systematic reviews of treatment efficacy should always include a thorough assessment of common and serious adverse events as well as efficacy in order to come to an informed and balanced decision about the utility of a treatment. A thorough assessment of adverse events should include data from RCTs, case–control and post-marketing surveillance studies and some of the other sources shown in Table 17.2.
Table 17.2 Other sources for data on adverse reactions to drugs.
| Resource | Source | Comments |
| Side Effects of Drugs Annuals | http://www.elsevier.com/books/book-series/side-effects-of-drugs-annual | Data 1–2 years old |
| Reactions Weekly | http://www.ovid.com/webapp/wcs/stores/servlet/product_Reactions-Weekly_13051_-1_13151_Prod-615 | Requires registration and fee |
| Drug Safety Update | http://www.mhra.gov.uk/Publications/Safetyguidance/DrugSafetyUpdate/index.htm | Drug safety bulletin of the Medicines and Healthcare Products Regulatory Agency (MHRA); issues freely searchable |
| Medicines Safety Update | http://www.tga.gov.au/hp/msu.htm#.Ur3Yx2RDt0o | Back issues and free email subscription available |
| European Medicines Agency | http://www.ema.europa.eu/ema/index.jsp?curl=pages/medicines/landing/epar_search.jsp&mid=WC0b01ac058001d124 | Free, searchable database of reports |
| MedWatch | http://www.fda.gov/medwatch/ | Searchable, database of spontaneous reports of adverse reactions to drugs maintained by the US Food and Drug Administration |
All websites last accessed May 2014.
Publication bias (i.e. the tendency that studies that are easy to locate are more likely to show ‘positive’ effects) is an important concern for systematic reviews [8]. It results from allowing factors other than the quality of the study to influence its acceptability for publication. Several studies have shown that factors such as sample size, direction and statistical significance of findings, or investigators’ perception of whether the findings are ‘interesting’, are related to the likelihood of publication [9].
Language bias may also be a problem, that is, the tendency for studies that are ‘positive’ to be published in an English language journal and also more quickly than inconclusive or ‘negative’ studies. A thorough systematic review should therefore include a search for high-quality, unpublished trials and not be restricted to journals written in English.
Studies are less likely to be published if they have negative results, especially if they have small sample size. By emphasizing only those studies that are positive, this type of publication bias jeopardizes one of the main goals of meta-analysis (i.e. an increase in power when pooling the results of small studies). The creation of study registers (e.g. http://clinicaltrials.gov/, https://www.clinicaltrialsregister.eu or http://www.anzctr.org.au; all last accessed May 2014) and advance publication of research designs have been proposed as ways to prevent publication bias.
For many diseases, published clinical trials are dominated by drug company-sponsored trials of new, expensive treatments, and in the absence of legislation that mandates publication of all clinical trials, many trials remain unpublished [10, 11]. This bias in publication can result in data-driven systematic reviews that draw more attention to those medicines. This problem underlies the need to develop and publish a protocol for a systematic review before the data are explored, as is the current practice with Cochrane reviews and those systematic reviews that are registered with PROSPERO. Question-driven systematic reviews answer the clinical questions of most concern to practitioners. In many cases, studies that are of most relevance to doctors and patients have not been done in the field of dermatology due to inadequate sources of independent funding.
Systematic reviews that have been sponsored directly or indirectly by industry are prone to bias by the overinclusion of unpublished positive studies that are kept ‘on file’ by that company and the exclusion of negative trials that are not published [10, 12]. Until it becomes mandatory to register all clinical trials conducted on human beings in a central register and to make all of the results available in the public domain, distortions may occur due to selective withholding or release of data.
Generally, reviews that have been conducted by volunteers in the Cochrane Collaboration are of better quality than non-Cochrane reviews [13]. However potentially serious errors have even been noted in up to a third of Cochrane reviews [14].
In general, the studies included in systematic reviews are analysed by at least two individuals. Data, such as numbers of people entered into studies, numbers lost to follow-up, effect sizes and quality criteria, are recorded on pre-designed data abstraction forms. Any differences between reviewers are usually settled by consensus or by an arbitrator. A systematic review in which there are large areas of disagreement among reviewers should lead the reader to question the validity of the review.
Are the results of the systematic review important?
Results in the individual clinical trials that make up a systematic review may be similar in magnitude and direction (e.g. they may all indicate that a treatment is superior to its comparator by a similar magnitude). Assuming that publication bias can be excluded, systematic reviews with studies that have results that are similar in magnitude and direction provide results that are most likely to be true and useful. It may be impossible to draw firm conclusions from systematic reviews in which studies have results of widely different magnitude and direction.
The key principle when considering combining results from several studies is that they should have conceptual homogeneity. Results of several different studies should not be combined if it does not make sense to combine them (e.g. if the patient groups or interventions studied are not sufficiently similar to each other). The trials should involve similar patient populations, have used similar treatments and have measured results in a similar fashion at a similar point in time. Although what constitutes ‘sufficiently similar’ is a matter of judgement, the important thing is to be explicit about one's decision to combine or not combine different studies.
There are two main statistical methods by which results are combined: random-effects models (e.g. DerSimonian and Laird) and fixed-effects models (e.g. Peto or Manzel-Haenszel) [15]. Random-effects models assume that the results of different studies may come from different populations with varying responses to treatment. Fixed-effects models assume that each trial represents a random sample of a single population with a single response to treatment (Figure 17.4). In general, random-effects models are more conservative (i.e. random-effects models are less likely to show statistically significant results than fixed-effects models). When the combined studies have statistical homogeneity (i.e. when the studies are reasonably similar in direction, magnitude and variability), random-effects and fixed-effects models give similar results.
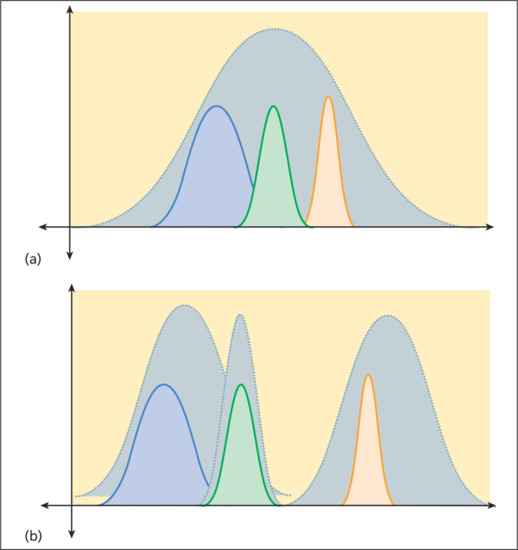
Figure 17.4 (a) Fixed-effects models assume that each trial represents a random sample (coloured curves) of a single population with a single response to treatment. (b) Random-effects models assume that the results of different trials (coloured curves) may come from different populations with varying responses to treatment.
The point estimates and confidence intervals of the individual trials and the synthesis of all trials in a meta-analysis are typically displayed graphically in a forest plot [16] (Figure 17.5). Results are most commonly expressed as the odds ratio of the treatment effect (i.e. the odds of achieving a good outcome in the treated group divided by the odds of achieving a good result in the control group), but can be expressed as risk differences (i.e. difference in response rate) or relative risk or risk ratio (probability of achieving a good outcome in the treated group divided by the probability in the control group). An odds ratio of 1 (null) indicates no difference between treatment and control and is usually represented by a vertical line passing through 1 on the x-axis. An odds ratio of greater or less than 1 implies that the treatment is superior or inferior to the control respectively. Risk ratios rather than odds ratios should be used for summarizing systematic reviews of common events because of the tendency of odds ratio to overestimate true risk in such conditions [17].
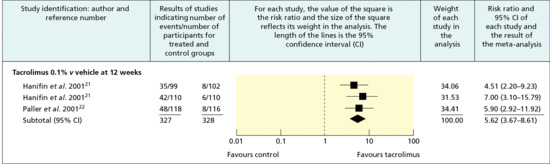
Figure 17.5 Typical forest plot showing the results of a meta-analysis of trials of tacrolimus 0.1% ointment versus vehicle in the management of moderate to severe atopic eczema. The x-axis represents the rate ratio of the investigator global assessment of response. (From Ashcroft et al. 2005 [44].
Reproduced with permission of BMJ Publishing Group Ltd.)
The point estimate of individual trials is indicated by a square whose size is proportional to the size of the trial (i.e. number of patients analysed). The precision of the trial is represented by the 95% confidence interval that appears in forest plots as the brackets surrounding the point estimate. If the 95% confidence interval (brackets) does not cross null (odds ratio of 1), then the individual trial is statistically significant at the level of P = 0.05.
The summary value for all trials is shown graphically as a parallelogram whose size is proportional to the total number of patients analysed from all trials. The lateral tips of the parallelogram represent the 95% confidence interval and if they do not cross null (odds ratio of 1), then the summary value of the meta-analysis is statistically significant at the P = 0.05 level. Odds ratios can be converted to risk differences and the number needed to treat (NNT) if the event rate in the control group is known (Table 17.3) [18, 19].
Table 17.3 Deriving numbers needed to treat (NNTs) from a treatment's odds ratio (OR)a and the observed or expected event rates of the control group.
| Odds ratio | ||||||||||
| 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 10 | ||
| Number needed to treat | ||||||||||
| 0.05 | 43 | 22 | 15 | 12 | 9 | 8 | 7 | 6 | 3 | |
| 0.1 | 23 | 12 | 9 | 7 | 6 | 5 | 4 | 4 | 2 | |
| CER or PEER | 0.2 | 14 | 8 | 5 | 4 | 4 | 3 | 3 | 3 | 2 |
| 0.3 | 11 | 6 | 5 | 4 | 3 | 3 | 3 | 3 | 2 | |
| 0.4 | 10 | 6 | 4 | 4 | 3 | 3 | 3 | 3 | 2 | |
| 0.5 | 10 | 6 | 5 | 4 | 4 | 3 | 3 | 3 | 2 | |
| 0.7 | 13 | 8 | 7 | 6 | 5 | 5 | 5 | 5 | 4 | |
| 0.9 | 32 | 21 | 17 | 16 | 14 | 14 | 13 | 13 | 11 | |
From http://www.cebm.net/index.aspx?o=1044 (last accessed May 2014).
aThe formula for converting ORs to NNTs is:
NNT = [{PEER*(OR – 1)} + 1] / [PEER*(OR – 1)*(1 – PEER)].
CER, control event rate (the rate of good events or outcomes in the control group); PEER, patient expected event rate (the rate of good events or outcomes in your patient or the population in which you are interested).
The most easily understood measures of the magnitude of the treatment effect are the difference in response rate and its reciprocal, the NNT [1, 2, 20]. The NNT represents the number of patients one would need to treat on average to achieve one additional cure. Whereas the interpretation of NNT might be straightforward within one trial, the interpretation of NNT requires some caution within a systematic review as this statistic is highly sensitive to baseline event rates. For example, if a treatment A is 30% more effective than treatment B for clearing psoriasis, and 50% of people on treatment B are cleared with therapy, then 65% will clear with treatment A. These results correspond to a rate difference of 15% (65 − 50) and an NNT of 7 (1/0.15). This difference sounds quite worthwhile clinically. However, if the baseline clearance rate for treatment B in another trial or setting is only 30%, the rate difference will be only 9% and the NNT now becomes 11; and if the baseline clearance rate is 10%, then the NNT for treatment A will be 33, which is perhaps less worthwhile. In other words, it does not make sense to provide one NNT summary measure within a systematic review if ‘control’ or baseline events rates differ considerably between studies. Instead, a range of NNTs for a range of plausible control event rates that occur in different clinical settings should be given, along with their 95% confidence intervals.
The data used in a meta-analysis can be tested for statistical heterogeneity by methods including the χ2 and I2 [2, 12, 21]. When there is evidence of heterogeneity, reasons for heterogeneity between studies – such as different disease subgroups, intervention dosage or study quality – should be sought [12]. Detecting the source of heterogeneity generally requires subgroup analysis which is only possible when data from many or large trials are available [1, 2]. Tests for statistical heterogeneity are typically of low power, so that failure to detect statistical heterogeneity does not ensure homogeneity.
Publication bias can be detected by using a simple graphic test (funnel plot), by calculating the ‘fail-safe’ N, or using the Begg rank correlation method, Egger regression method and others [22]. These techniques are of limited value when less than 10 randomized controlled trials are included. Testing for publication bias is almost never possible in systematic reviews of skin diseases because of the limited number and sizes of trials.
Sometimes, the robustness of an overall meta-analysis is tested further by means of a sensitivity analysis. In a sensitivity analysis the data are re-analysed excluding those studies that are suspect because of quality or patient factors, to see whether their exclusion makes a substantial difference in the direction or magnitude of the main original results. In some systematic reviews in which a large number of trials have been included, it is possible to evaluate whether certain subgroups (e.g. children versus adults) are more likely to benefit than others. Subgroup analysis is rarely possible in dermatology because few trials are available.
The conclusions in the discussion section of a systematic review should closely reflect the data that have been presented within that review. The authors should make it clear which of the treatment recommendations are based on the review data and which reflect their own judgements. The approach developed by the Grading of Recommendations, Assessment, Development and Evaluations (GRADE) working group (http://www.gradeworkinggroup.org/index.htm; last accessed May 2014) links the quality of evidence to clinical recommendations by means of summary of findings tables that are used in Cochrane reviews. The GRADE approach assesses methodological flaws of included studies, the consistency of study results, how generalizable the results are to a broader group of patients, and the magnitude of effect of treatment.
Many reviews in dermatology find little evidence to address the questions posed. The review may still be of value, especially if the question addressed is an important one [1, 23]. For example, the systematic review may provide the authors with the opportunity to call for primary research in an area, and to make recommendations on study design and outcomes that might help future researchers [24].
Can the results of the systematic review be applied to your specific patient?
Applying external evidence to the patient in front of you is one of the most difficult steps of evidence-based medicine. Having identified some relevant and valid information from a systematic review in relation to a clinical question generated by a patient encounter, three questions now need to be asked in order to guide the application of such information to that patient (see Box 17.4).
Firstly, physicians should ask themselves whether there are any compelling reasons that the results should not be applied to the patient, rather than expecting a perfect match of the study participants and patient. Only if the answer is ‘yes’ are the study's results not applicable to the patient. Participants in clinical trials may be different from the patient who originally prompted you to ask an evidence-based question in obvious biological ways such as age, sex and clinical disease type, but in most circumstances these differences do not prevent you from making some useful generalizations from the literature. Perhaps one of the most frequent problems encountered is that of having to generalize trials of adult therapy to children, in whom RCTs are rarely performed. Yet children can suffer almost all of the ‘adult’ skin diseases, and practitioners frequently have no choice but to use adult-based data as a means of informing treatment decisions.
Secondly, the outcomes desired by the patient should have been included in or be deducible from the outcomes of the systematic review. Finally, the benefits of the intervention should outweigh the risks and the intervention should be available and affordable.
Critically appraising individual clinical trials [1,2,25,26]
Are the results of the trial valid?
To determine whether an individual clinical trial is valid, pay particular attention to the features that strengthen clinical trials and help validate their conclusions (Box 17.5). The ‘big three’ that should always be assessed are:
- Is the method of generating the randomization sequence and subsequent concealment of allocation of participants clearly described and appropriate?
- Were participants and study assessors masked to the intervention?
- Were all those who originally entered the study accounted for in the results and analysis (i.e. was an intention-to-treat analysis performed)?
Ideally, patients should be randomly assigned to treatment groups to avoid the introduction of biases and to distribute intrinsic prognostic factors equally among treatment groups. Randomization controls patient selection and evaluation bias by physicians and study personnel. Non-randomized studies have limited value in distinguishing useful from useless or even harmful therapy. When compared with RCTs, studies in which patients are not allocated randomly more commonly show larger effects, many of which are false positive. For example, the belief that azathioprine reduces the dose of corticosteroids necessary to treat bullous pemphigoid was suggested by several uncontrolled or non-randomized studies. However, a randomized trial of the effects of azathioprine on corticosteroid dose in patients with bullous pemphigoid and a systematic review of interventions for bullous pemphigoid indicated that azathioprine had no or negligible effect on remission or corticosteroid doses [27, 28].
Randomization has the disadvantage of depending on chance for an equal statistical distribution of prognostic factors among groups. Therefore, it is always important to identify known prognostic factors such as disease severity and compare their distribution among treatment groups at baseline. The common practice of assigning P values to differences in characteristics at baseline is inappropriate. Demographic and known prognostic factors may not be equally distributed among treatment groups when patients are randomly assigned to them. However, the impact of the unequal distribution of prognostic factors on treatment results should be assessed. Inequality of groups in randomized trials can usually be adjusted for in appropriate analyses. Inequality of groups is a more significant problem in studies with few patients.
When patients are assigned randomly, the method used to randomize should be reported. The most widely accepted and unbiased methods are to use sealed random numbers obtained from tables or random numbers generated by computers. In this method, patients are assigned a random number after they are admitted to a trial. That number has been previously assigned to a treatment group and the assignment is unknown to the patient and the investigator. Correct randomization or concealment of assignment is often not done in published studies, and the methods of randomization are rarely reported. Many commonly encountered methods of randomization (e.g. on the basis of the admitting team, alternative assignment, odd or even days of entry, birth dates, social security numbers or day of the week) can lead to significant introduction of selection bias. For example, a physician who would like a new treatment to be shown to be superior in efficacy to an older treatment may be able to enter patients most likely to respond to treatment on even days and patients least likely to respond on odd days, if he or she knows that the new treatment is assigned on even days and the older treatment is assigned on odd days.
Concealment of treatment allocation refers to the steps taken by the trialists to conceal the allocation of participants to the intervention groups from those recruiting trial participants, and is a crucial step in the construct of an RCT. Concealing the sequence from recruiters is adequate if investigators and patients cannot foresee the assignment to intervention groups (e.g. numbered and coded identical sealed boxes prepared by a central pharmacy or sealed opaque envelopes). It is inadequate if the allocation schedule is open for the recruiting physician to view beforehand (e.g. unsealed envelopes).
The randomization list should be kept away from enrolment sites (e.g. by a central clinical trials office or pharmacy). Internet randomization by a third party, whereby details of a new, potentially eligible trial participant are entered irrevocably onto a trial database before an allocation code is offered, is another very secure way of concealing allocation.
It is important to make the evaluation of the outcome of a trial as masked as possible to avoid the introduction of bias. Masking can refer to at least four groups of people: those recruiting patients, the study participants themselves, those assessing the outcomes in study participants, and those analysing the results. The masking of physicians and patients is especially important when subjective outcomes such as pain are being measured. The masking of patients and evaluators also ensures that ancillary therapies and outcome evaluations are applied equally, thus minimizing performance bias. A patient who is known to be receiving a new treatment may be observed more closely, may receive better ancillary care and may have different expectations than a control patient. Changes in disease status may receive greater (or lesser) emphasis and adverse events may similarly receive more (or less) attention. Masking is less of an issue for some studies that use very objective outcomes such as death, since the risk of detection bias is low for such an outcome.
However, masking is often not possible. Many treatments produce skin changes that make it apparent what treatment is being used. For example, the drying effects of topical and systemic retinoids and the tanning effects of UVB therapy make the recipients of those therapies readily apparent. An unmasked study may still be valid, but the designers of an unmasked study must make allowances for the possibility that bias may have been introduced and should increase the statistical rigour for demonstrating differences.
The whole purpose of randomization is to create two or more groups that are as similar to each other as possible, the only difference being the intervention under study. In this way, the additional effects of the intervention can be assessed. A potentially serious violation of this principle is the failure to take into account all those who were randomized when conducting the final main analysis, for example participants who deviate from the study protocol, those who do not adhere to the interventions and those who subsequently drop out for other reasons. People who drop out of trials tend to differ from those who remain in them in several ways. People may drop out because they encounter adverse events, get worse (or no better) or simply because the proposed regimen is too complicated for them to follow. They may also drop out because the treatment is working so well. Ignoring participants who have dropped out in the analysis is not acceptable as their very reason for dropping out is likely to be related in some direct or indirect way to the study intervention. Excluding participants who drop out after randomization potentially biases the results. One way to reduce bias is to perform an intention to treat (ITT) analysis, in which all those initially randomized are included in the final analysis.
Unless one has detailed information on why participants dropped out of a study, it cannot be assumed that analyses of those remaining in the study to the end are representative of those randomized to the groups at the beginning. Failure to perform an ITT analysis may inflate or deflate estimates of treatment effect. Performing an ITT analysis is regarded as a major criterion by which the quality of an RCT is assessed.
It may be entirely appropriate to conduct an analysis of all those who remained at the end of a study (a ‘per protocol’ analysis) alongside the ITT analysis. Discrepancies between results of ITT and per protocol analyses may indicate the potential benefit of the intervention under ideal compliance conditions and the need to explore ways of reformulating the intervention so that fewer participants drop out of the trial. Discrepancies may also indicate serious flaws in the study design [29].
A considerable degree of detail needs to be provided in the methodology section of a published clinical trial. This need has led to the development of reporting guidelines, for example the Consolidated Standards of Reporting Trials (CONSORT) (http://www.consort-statement.org/download/Media/Default/Downloads/CONSORT%202010%20Checklist.doc; last accessed May 2014). Most of the top dermatology journals now insist that all RCT submissions are reported according to the CONSORT checklist.
Other features that strengthen the validity of trials [1, 2, 3, 21, 22]
In evaluating a clinical trial in dermatology, look for clinical outcome measures that are clear cut and clinically meaningful to you and your patients. For example, in a study of a systemic treatment for warts, the complete disappearance of warts is a meaningful outcome, whereas a decrease in the volume of warts is not. Historically, three principle methods are used to determine patient outcomes in dermatological clinical trials. The first involves examining patients before, during and at the conclusion of treatment, and reporting how the patients appear at the various time points. The second involves determining the degree of improvement during treatment [30]. A third method, determining the impact of therapy on the quality of the patient's life, is being increasingly used in dermatological trials.
An example of the first method is commonly encountered in therapeutic trials of psoriasis. A common practice is to assign numerical values to the amount of erythema, scaling and degree of infiltration, to determine the area of the body surface involved, and to formulate an ‘index’ by calculating a derivative of some product of these four numbers. The overall condition of the patient can then be represented by this index. A common example is the psoriasis area and severity index (PASI) that ranges from 0 to 72 [31].
The major problem with indices is that they confound area of involvement with severity of disease. For example, a patient with thick plaque-type psoriasis of the knees, elbows and scalp may have the same index as a patient with diffuse but minimal psoriasis of the trunk and arms. Whereas the former patient is notoriously difficult to treat, the latter will generally respond rapidly and easily to many forms of therapy. The second problem with indices is that they lend an air of accuracy to the analysis and presentation of data that is not warranted. For example, Tiling-Grosse and Rees demonstrated that physicians and medical students were poor at estimating the area of skin disease, and, therefore, some of the components that make up indices may be inaccurate [32]. Finally, calculating the means, differences in means and percentages of change in indices in response to treatment often do not convey an accurate clinical picture of the changes that have occurred.
The second method of assessment groups patients according to their degree of improvement. Treatments are then compared by their ability to move patients to higher degrees of improvement. There are two major problems with this form of assessment. The first is that the categories of improvement are often not well defined. The second problem is that the categories are not additive. That is, 60–80% improvement is often assumed to be twice as good as 20–40%, although no such numerical relationship exists between these subjectively defined categories.
To be most useful, the outcome variables to measure must be clearly defined, be as objective as possible, and have clinical and biological significance. The best indices and scales are those that accurately reflect the state of the disease and those for which validity and reliability have been verified by previous work. The development of scales and indices for cutaneous diseases, and testing their validity, reproducibility and responsiveness has been inadequate. Therefore a lack of clearly defined and useful outcome variables remains a major problem in interpreting dermatological clinical trials.
Several groups in medicine are now developing the concept of core outcome measures, a set of which should always be included in clinical trials (http://www.comet-initiative.org/; last accessed May 2014). The measures are designed to ensure that the key features or domains of a disease are included and that the best instrument for measuring that domain is used. The best known core outcome sets are for arthritis. Similar groups, such as the Harmonising Outcome Measures for Eczema (HOME), are developing a similar approach in the field of dermatology [33].
Until better scales and core outcome sets are developed, trials with the simplest and most objective outcome variables are the best. They lead to the least amount of confusion and have the strongest conclusions. Thus, trials in which a comparison is made between death and survival, patients with recurrence of disease and those without recurrence, or patients who are cured and those who are not cured are studies whose outcome variables are easily understood and verified. For trials in which the outcomes are less clear-cut and more subjective in nature, a simple ordinal scale is probably the best choice. The best ordinal scales involve a minimum of human judgement, have a precision that is much smaller than the differences being sought and are sufficiently standardized that they can be used by others and produce similar results.
In addition to being clearly defined, outcome variables should have clinical and biological significance. For example, in a therapeutic trial of patients with severe acne, treatment was associated with a decrease in lesion count from a mean of 400 to a mean of 350. This numerical difference may be of statistical significance, but it does not convey the clinical significance. This result may mean that some patients with severe acne cleared completely whereas other patients remained the same or got worse. It could also mean that most patients got slightly better. Furthermore, does an individual patient look better when their lesion number has been reduced from 400 to 350? Are scarring and complications less?
To strengthen clinical trials and help validate their conclusions, the outcome variables should be few in number and should be chosen before initiation of the study. Having many outcome variables increases the likelihood that spurious, chance differences will be detected. An ineffective treatment may be claimed to be efficacious when tested using poorly designed outcome assessment tools. Conversely, an effective therapy may be found ineffective by an insensitive scale.
Special precautions are recommended when dealing with ‘substitute or surrogate end points’, especially when no differences are detected in clinically important outcomes. Examples of such end points include CD4 : CD8 ratios instead of survival in studies of treatments of AIDS; antinuclear antibody levels or sedimentation rates instead of clinical measures of disease activity in lupus erythematosus; and volume of warts instead of proportion of patients cleared of warts. Carefully chosen and validated surrogate end points often allow studies to provide answers to questions that would typically require much larger or longer trials if the targeted clinical end points were utilized. For example, a well-designed, short clinical trial may be sufficient to demonstrate that a new drug effectively lowers serum cholesterol or that another drug is effective in controlling hypertension. In both cases much longer and larger studies would be required to demonstrate that the cholesterol-lowering drug and the antihypertensive drug reduced morbidity and mortality from atherosclerotic and hypertensive cardiovascular diseases, respectively. Surrogate end points must, however, correlate with clinical outcomes and their validity must be demonstrable in prior studies.
Are the results of the clinical trial important? [1, 2, 21, 22]
Once sound, clinically relevant outcome measures are chosen, the magnitude of the difference between the treatment groups in achieving these meaningful outcomes, the NNT and the precision of these estimates should be determined.
Examples of the application of the concepts of NNT and confidence intervals are found in a trial comparing placebo, aciclovir, prednisolone and aciclovir–prednisolone in the treatment of herpes zoster [34]. At day 30 of the trial, 48 of 52 patents treated with aciclovir were totally healed compared to 22 of 52 patients who received placebo. The response rates for aciclovir and placebo were 0.92 and 0.42, respectively, and the difference in response rates was 0.5. The NNT was 2 (1/0.5). This result means that for every two patients treated with aciclovir instead of placebo, one additional patient would be totally healed by day 30. The 95% confidence interval for the difference in response rates is from 0.35 to 0.65, and the 95% confidence interval for the NNT is from 2 to 3.
Misinterpreting trials that fail to show statistically significant differences among treatments is a common error of interpretation in clinical trials in dermatology. It is important to remember that ‘not statistically significant’ means that a difference has a reasonably high probability of having been due to chance; it does not mean that there is no difference or that treatment is necessarily ineffective. Significant differences in treatment effects in comparison trials may be missed if the number of subjects tested is small. For example, in a 1978 survey of 71 published trials with negative results, Freiman et al. found that a 25% or 50% improvement in outcome might have been missed in 57 (80%) and 34 (48%) of the studies, respectively [35]. A follow-up study conducted by Moher et al. in 1994 indicated that 25% or 50% improvements in outcome might have been missed in 84% and 64% of 102 negative studies, respectively [36]. The sample sizes of many dermatological trials are often inadequate to detect clinically important differences. For example, 58 clinical trials with negative conclusions, published in three British dermatological journals over 4 years, were reviewed to determine the risk of their having missed an effective treatment. All but one of the 44 evaluable trials had a greater than one in 10 risk of missing a 25% relative treatment difference (median risk 81%), and 31 of the trials (70%) were so small that they had a greater than one in 10 risk of missing a 50% relative treatment difference (median risk 42%) [37].
Can the results of the trial be applied to your specific patient?
Applying evidence from a clinical trial to specific patients is similar to the process used to apply the results of a systematic review to specific patients (see previous section). Four questions now need to be asked in order to guide the application of such information to that patient (see Box 17.5).
Critically appraising a study about a diagnostic test [1, 2, 3]
Are the results valid?
To be valid, studies about diagnostic tests should include masked comparison with a criterion (‘gold’) standard, evaluation in an appropriate spectrum of patients and consistent application of the criterion standard (Box 17.6). Few studies in dermatology meet this standard.
Are the results important?
Important terms and concepts that must be understood to determine whether the results of a paper about a diagnostic test are clinically important include the likelihood ratio, pre-test probability, post-test probability and threshold for action. The likelihood ratio is the percentage of people with the disease who have a positive test divided by the percentage of people who do not have the disease who have a positive test. The likelihood ratio is traditionally taught as being the sensitivity divided by 1 minus the specificity: it provides an estimation of how much higher the likelihood of the disease is, given a positive test (post-test probability), compared with the probability before the test is done (pre-test probability). An ideal test is one that will almost always be positive when the disease is present and negative when the disease is absent. Thus, it is one with a high sensitivity and specificity. Such a test would have a very high likelihood ratio.
In order for the likelihood ratio to be useful, one has to have an idea of how likely the disease is to be present before the test is done (i.e. the pre-test probability) and a sense of how certain one needs to be to conclude that the patient has the disease and to act on it (i.e. the threshold for action) [38]. The pre-test probability is determined from available published data or based on physician experience and judgement. Once the pre-test probability is known or estimated and the likelihood ratio determined, a nomogram can be used to estimate the post-test probability (Figure 17.6).

Figure 17.6 Nomogram for determining the post-test probability. To determine the post-test probability, draw a straight line through the pre-test probability and the likelihood ratio and read the post-test probability on the right.
If the nomogram is not available, the calculations can be done manually after conversion of probabilities to odds. The odds of disease is defined as the probability of disease divided by 1 minus the probability (odds = probability/1 – probability). For a defined group of individuals or patients, it can also be calculated as the ratio of the number of those with disease to those without disease. Thus, if the probability of (proportion with) a disease is 0.20 (20%), the odds of that disease are 0.20/1 – 0.20, or 0.20/0.80, or 1 : 4. This result means that for every person with the disease, there are four people without the disease. The post-test odds are equal to the pre-test odds times the likelihood ratio (post-test odds = pre-test odds × LR). The formula (probability = odds/odds + 1) is used to convert odds back to probability.
For example, suppose that, based on clinical judgement, the estimated probability that a patient with a cluster of vesicles on his cheek has herpes zoster is 0.6 (60%), then his odds of having herpes zoster are 1.5 : 1 (0.6/1 – 0.6). Assume, for this example, that the sensitivity and specificity of a direct fluorescent antibody (DFA) test for herpes zoster are 80% and 96%, respectively. Therefore, the likelihood ratio for a positive DFA is 20 (0.80/1 – 0.96). If this patient's DFA test is positive, his post-test odds are 30 (1.5 × 20) and the post-test probability of herpes zoster is 0.97 (97%) (30/30 + 1). This probability is certainly high enough to act upon.
Whether formally or informally, physicians develop thresholds of certainty at or above which they are comfortable with establishing a diagnosis and acting on the diagnoses. Action may take the form of communicating the diagnosis or prognosis to the patient, prescribing treatment or referring the patient. When historical and physical evidence leads a clinician to suspect a diagnosis, but the degree of certainty does not exceed the threshold for establishing a diagnosis, a test is done to increase the probability that the disease is present above the clinician's threshold for action [33]. Diagnostic studies should always be interpreted in the context of specific clinical encounters so that the diagnostic value of the test can be assessed [39, 40]. Studies reporting diagnostic tests in dermatology should adhere to established international reporting standards [26].
Can the results of the diagnostic study be applied to your specific patient?
The key questions to ask to determine whether the results of a diagnostic study can be applied to a specific patient are shown in Box 17.6.
Critically appraising a study about adverse events (case–control and cohort studies) [1, 2, 41]
Are the results valid?
To be valid, studies about the harmful effects of exposures should include cohorts with comparable groups of exposed and unexposed individuals, or cases and controls, objective outcome measures and adequate follow-up. The effects of selection bias when choosing cases and controls need particular consideration in the absence of randomization. In addition, the results should make clinical and biological sense (Box 17.7).
Are the results important? [1, 2, 3, 33]
Important terms and concepts that must be understood to determine whether the results of a paper about harmful effects of exposures are clinically important include case–control and cohort studies, relative risk and odds ratios. In a cohort study a group of individuals who are exposed to an agent is compared with an appropriately selected unexposed control group and both groups are followed until an event of interest occurs or for a pre-specified length of time. The association of exposure to the harmful outcome is expressed as the relative risk (Box 17.7). A relative risk of 1 implies no association. If the relative risk is greater than 1, then the result implies a positive association between exposure and the harmful outcome. If it is less than 1, then the implication is of an inverse association. However, in order to infer a causal association reflected by either an increase in risk (relative risk of more than 1) or a protective effect (relative risk less than 1), it is important to evaluate the validity and precision of the relative risk estimate. The precision can be readily assessed by means of the 95% confidence interval. A confidence interval that does not include 1.0 denotes a statistically significant association. Because the most likely result of a study is the point estimate (i.e. the reported result), the observed association (expressed by the point estimate) may be causal, even if the confidence interval includes 1.0 as a result of a small sample size. Other criteria such as dose–response effect, consistency, biological plausibility and specificity need to be considered when inferring causality from observational data [42].
Case–control studies can be used when the undesirable outcome (e.g. lymphoma) is recognized and the causative agent not yet discovered. They are also used when there is a very long time lag between exposure and outcome or when the frequency of adverse events is very small. In a case–control study, patients with a disease of interest are compared with appropriately selected controls. The odds of exposure to suspected aetiological agents are ascertained in the cases and controls (Box 17.7). The odds of an event are the ratio of the number of events to the number of non-events. Events are exposures to potentially harmful risk factors in case–control studies. The odds of exposure of cases are divided by the odds of exposure among controls to derive the odds ratio, which is a good estimate of the relative risk when the outcome (e.g. disease, death) is relatively rare (i.e. when it is less than 5% in exposed subjects). An odds ratio of 1 implies no association. If the odds ratio is greater than 1, then the result implies a positive association between exposure and the harmful outcome. If the odds ratio is less than 1, then the result implies a protective effect of the exposure. As noted above, it is important to evaluate the validity and precision of the odds ratio estimate by examining the 95% confidence interval.
For example, suppose a case–control study was performed to study the relationship between limb deformity and exposure to thalidomide. The results of the study indicated that patients with limb deformities were more likely than controls to have been exposed to thalidomide in utero. The odds ratio for thalidomide exposure was 3.5 and the confidence interval was from 1.8 to 6.6. Thus the odds that patients with limb deformities were exposed to thalidomide in utero were 3.5 times the odds of thalidomide exposure in controls. Since the odds ratio is greater than 1, and its 95% confidence interval does not include 1, the result implies the positive association between thalidomide use and limb deformities was not likely to have been due to chance. These results (an odds ratio of 3.5 and confidence interval of 1.8–6.6) were actually the results of a study by Wolf et al. who studied the relationship between sunscreen use and melanoma in a case–control study in Austria [43]. Their results indicated that patients with melanoma were more likely than controls to report having used sunscreen often. In order to infer causality it is important to assess whether the data could have resulted from confounding (i.e. the association between exposure and outcome can be explained by other factors such as age, sex or bias (e.g. people with melanoma may be more likely to recall sun protective behaviour)) and that the results are biologically plausible.
To add confusion to an already difficult area, clinical researchers will often report results of meta-analyses, cohort studies and RCTs using odds ratios. Odds ratios are used because they have stronger statistical properties than other measures [33]. For example, odds ratios can take any value between zero and infinity, are symmetrical in a log scale and can be used to make adjustments for confounding factors using multiple regression. Unfortunately, they are the measure of association least intuitively understood. If a meta-analysis, controlled trial or cohort study is reported using odds ratios, the relative risk, difference in response rates or NNT can often be calculated if the primary data are provided. Alternatively, these more readily understandable measures can be derived if the number of subjects in each group, odds ratio and overall event rate are provided (http://www.cebm.net/index.aspx?o=1044; last accessed May 2014).
Can the results be applied to your specific patient?
The key questions to ask to determine whether the results of a study of adverse events (usually a case–control or cohort study) can be applied to a specific patent are shown in Box 17.07.
Conclusions
Evidence-based medicine is the use of the best current evidence in making decisions about the care of individual patients. It is predicated on asking clinical questions, finding the best evidence to answer the questions, critically appraising the evidence, applying the evidence to specific patients and saving the critically appraised evidence. The EBM approach is most appropriate for common, frequently encountered conditions.
Results from well-designed clinical studies on patients are near the top of the hierarchy of evidence used to practice EBM. Recommendations about treatment, diagnosis and harm made in this textbook and in other sources should take into account the validity, magnitude, precision and applicability of the evidence upon which it is based.
Evaluating the data in clinical research papers and a shortcut method for reading clinical research papers
Evaluating the data in clinical research papers [1]
Are the data adequately reported?
The authors of a study should present their results in sufficient detail to allow the reader to perform his or her own preferred analysis of the data. At a minimum, the presentation of interval data (i.e. discrete or continuous data such as lesion counts or area of involvement) should include a summary measure of the centre of the data for each group and a measure of the variability of the data. The mean and median are most commonly used to indicate the centre of the data. The mean is simply calculated as the sum of the data points divided by the total number of data points. The mean is the most appropriate choice for normally distributed data (i.e. data that are distributed in the shape of the bell curve). The median is a better choice for data that are skewed or contain outliers (Figure 17.7a, b). The median for an odd number of data points is the value in the middle when the data are ordered from lowest to highest. The median for an even number of data points is determined by taking the mean of the two numbers in the middle when the data points are ordered from lowest to highest. Half the data points fall above and half fall below the median. The magnitude of the difference between the mean and the median is a crude indicator of the degree of skewing. If the difference is none or small, the data are or approach normal (i.e. are symmetrical); if the difference is large the data are skewed.
Figure 17.7 Hypothetical final lesion counts in a clinical trial of treatments X, Y and Z. The same data are displayed or summarized in each panel.A graphical display of all of the data points (a) gives an accurate description of the magnitude and distribution of the results. Commonly used summary statistics (b).The mean with error bars consisting of 1 SD (c) or 1 SE (d) provide little useful information even for the normally distributed response to treatment X and are totally misleading for treatment Y, which is skewed, and treatment Z, which has outliers.A box plot of the data (e) shows the median (line within the box), the interquartile range (top and bottom of the box) and adequately represents skewed data (note the asymmetry of the median within the box in the Y plot) and the presence of outliers (note the asymmetry of the median within the box in the Z plot and the outliers indicated by an asterisk and open circle).The 95% confidence interval about the median (f) adequately represents skewed data and the presence of outliers. If the 95% confidence intervals around two means or medians do not overlap, you can be confident at about the 95% level that the two population means or medians are different.
The standard deviation, range, interquartile range and 95% confidence intervals are commonly used to indicate the variability or spread of the data (Figure 17.7c–f). The standard deviation (SD) is the square root of the average squared deviation of values from the mean. That is:
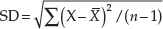
The standard deviation is an important summary statistic for normally distributed data only. For normally distributed data, approximately 68% of the data points will lie within the range from the mean minus 1 SD to the mean plus 1 SD; and 95% of the data points will lie within the range from the mean minus two times the SD to the mean plus two times the SD. These relationships do not apply to skewed data or small data sets that contain outliers. Note in Figure 17.7c that the mean and standard deviation do not adequately describe the centre of the data or its distribution for skewed data or data with outliers (treatments Y and Z).
The range is the interval from the highest to the lowest data points. The range may be a good indicator of variability for data that are tightly arranged around the mean and for small data sets. The range is greatly influenced by outliers and may not give an adequate indication of skewed data. Therefore the range is not a good descriptive statistic for skewed data sets or for data with outliers (Figure 17.7a, b).
The interquartile range is the interval that contains the middle 50% of the data points. It excludes the highest 25% of the data points and the lowest 25%. The interquartile range is a reasonable descriptive statistic to describe skewed data and data with outliers (Figure 17.7e).
Confidence intervals are the best way to present the degree of uncertainty of normally distributed data as well as skewed data or data with outliers (see discussion of confidence intervals later). The 95% confidence interval around the mean can be calculated for normally distributed data using the sample mean, standard error and the t distribution. For skewed data, the confidence interval around the median should be used (Figure 17.7f).
The standard error (SE) is the standard deviation divided by the square root of the number of data points (SE = SD/√n). Unfortunately, the standard error is commonly but incorrectly used to summarize the variability of data. This choice is made because of tradition and because the SE is always smaller than the SD and 95% confidence interval and, therefore, looks better (Figure 17.7c, d, f). The standard error is correctly used to analyse normally distributed data in inferential statistics (see discussion of the t-test later). The common practice of reporting the mean ± SE is firmly ingrained in the medical and scientific literature but is often misleading and inappropriate, and should be discouraged. The standard error is an important and useful statistic only for normally distributed data sets. It is used to make predictions or inferences about the population from which the sample is chosen. That is, for large, normally distributed data sets, the chance that the true or population mean (from which the sample was drawn) will lie outside the range from the sample mean minus two times the SE to the sample mean plus two times the SE is only 5%. The relationship between the sample mean, the population mean and the standard error does not apply to skewed data or small data sets that contain outliers.
Descriptive statistics are at best incomplete summaries of the data; considerably more information may be conveyed by graphic displays (see Figure 17.7) [2]. Figures that show individual observations are an excellent tool for presenting small data sets, and data that are skewed or have outliers (see Figure 17.7a) [2]. Unfortunately, such diagrams are underutilized in the scientific and medical literature. Graphic displays of data using ‘error bars’ showing 1 SD or 1 SE depict at best 68% of the sample or 68% confidence intervals, respectively, and are therefore misleading and should be avoided or approached with scepticism (see Figure 17.7c, d).
Categorical data are preferably presented in tables in which the treatments and outcomes are represented in rows and columns. Examples of categorical outcomes include cured and not cured, survived and died, and minimal, moderate and marked improvement. Categorical outcomes should be clearly defined, limited in number, clinically important and declared before the trial is begun.
Are the data subjected to statistical testing and are the tests used correctly?
Observed differences in outcome in clinical trials may be due to chance alone. It is therefore imperative that statistical analyses be performed to verify that the results are from treatment and not from chance. This admonition is especially true for trials containing few patients, as is the case for many published dermatological trials.
Statistical methods
Understanding P
Understanding the meaning of P is fundamental to understanding and interpreting statistical testing. In the simplest terms, all clinical trials begin with the null hypothesis – that the effects of each treatment are the same. If the results of the trial indicate that the outcomes of treatment are different, then a statistical test is performed to determine whether the difference could be from chance or sampling variation alone. If chance is not a likely explanation of the difference, the null hypothesis that the outcomes of each treatment are the same is rejected. P represents the probability that a difference as large as the observed difference might arise by chance if the treatment outcomes are the same.
The error of believing that a difference in treatment outcomes exists, when in fact there is no difference and the observed differences were from chance or sampling variation alone, is referred to as a Type I or α error. The statement that ‘the difference was statistically significant (P = 0.05)’ means that the probability that a difference as large as the observed difference might arise by chance is one in 20 and that the author will accept this degree of chance as being sufficiently unlikely that the null hypothesis (that the treatment outcomes are the same) can be rejected. Conversely, the statement that ‘the difference was not statistically significant (P = 0.10)’ means that the probability that a difference as large as the observed difference might arise by chance was one in 10 and that the author will not accept this degree of chance as being sufficiently unlikely that the null hypothesis (that the treatment outcomes are the same) can be rejected. It is important to remember that ‘not significant’ means that a difference is not proven; it does not mean that there is no difference.
The acceptance of a significance level of 0.05 as the cut off for rejecting the null hypothesis is a tradition based on quality control standards and is not an absolute truth. At times more stringent standards are required and, paradoxically, tests that do not meet the P = 0.05 standard sometimes may be significant. For example, a trial of a new chemotherapeutic agent involving 30 randomized patients with metastatic melanoma produced a 5-year survival of seven of 15 patients treated with the new agent, and three out of 15 in control patients treated with conventional surgery, chemotherapy and radiation. Whereas the result does not achieve statistical significance when compared by χ2 testing (see later section) (Yates corrected χ2 = 1.35; P = 0.25), the result is, nonetheless, potentially significant. If the therapy is beneficial and the estimated difference in response rates is the true difference in response rates, it may result in the saving of 2528 lives annually in the USA (based on 9480 deaths from melanoma annually and the improvement in survival in this hypothetical example). Because of the biological and clinical importance of the results suggested by the study, the treatment should be subjected to study in a larger patient population with more power to detect a difference, if one exists (see discussion of power later). Others might argue that the adherence to the 95% standard (P = 0.05) should be relaxed in cases like this one. The potential benefit of the treatment may be revealed by the use of confidence intervals (see discussion of confidence intervals later).
Investigators should indicate what statistical procedures were utilized to compare results. Simply stating that the difference was statistically significant (P <0.05) does not constitute an adequate description of the statistics used. The exact procedure used (e.g. t-test or χ2) and the results obtained must be specified. The t-test and the analysis of contingency tables (e.g. χ2 and Fisher exact test) are the most commonly employed procedures and should be understood by all physicians.
The t-test
The t-test is the most commonly used statistical test in the biomedical literature. It is used to determine whether the difference in the means of two samples is from chance (sampling variation) alone. It should be emphasized that the t-test at a significance level of 0.05 is designed to compare the difference in the means of only two samples or populations. The t-test has additional important restrictions. It should be used to compare the means of interval data that are normally distributed. The data analysed by the t-test should be sufficiently large, should not contain outliers, should be statistically independent and the variability of the two treatment groups should be similar. In most instances a two-sided t-test is appropriate. When a one-sided t-test is performed the reasons should be specified. A two-sided test should be used when either treatment may be superior. A one-sided test is used when the authors are only interested in whether one treatment is better than the comparator [3].
The unpaired t-test should be used to analyse two different groups (e.g. patients receiving alternative treatments). The paired t-test should be used to analyse the effects of two different treatments on the same patients (e.g. in a cross-over or left–right comparison study).
Statistical analysis using the t-test can be illustrated using data from a study comparing calcipotriol and betamethasone ointments in the treatment of stable plaque psoriasis [4]. In this multicentre RCT, 201 and 200 patients were randomized to treatment with calcipotriol and betamethasone, respectively. Outcomes were measured by changes in PASI scores. At the end of 6 weeks of treatment the improvement (decrease) in PASI scores were 5.50 and 5.32 for calcipotriol and betamethasone, respectively. The statistical significance of the small difference in the change in PASI scores was evaluated using an unpaired t-test. The t value and corresponding significance level can be determined using computer programmes or calculated using a t distribution table and the formula. Not surprisingly, the result indicated that the difference was not statistically significant (P = 0.76). Thus, the trial failed to demonstrate a difference between the two treatments.
Misuse of the t-test was one of the most commonly encountered errors in the use of statistics found by Gore et al. in their review of the use of statistical methods in the British Medical Journal [5]. They found that 52% (32/62) of analytical reports that utilized statistical analyses contained at least one error in the use of statistics. Eleven of the errors were misuse of the t-test. The errors included using the t-test to analyse data that were not normally distributed or had different variability, and using an unpaired t-test to analyse paired data. Another commonly encountered error in the use of the t-test is its use to compare the means of more than two samples. This error in the use of the t-test occurred in 61% and 44%, respectively, of articles that used statistical analyses published in Circulation Research and Circulation in 1977 [6].
The t-test should not be used to analyse data that are skewed, or data in which the variability (standard deviation) is very different between treatment groups. Nor should it be used to analyse small data sets because it is impossible to verify that small data sets are normally distributed. In these situations, the Mann–Whitney U test, the distribution-free equivalent of the t-test, may be used for unpaired data, and the Wilcoxon test can be used for paired data. The t-test also should not be used to compare more than two groups because it ignores possible associations among groups and it increases the likelihood that spurious results will be obtained. Testing of the means of more than two groups can be performed with different forms of analysis of variance.
Contingency tables
Chi-square is the most commonly used test to determine whether the categorical data in contingency tables differ because of chance alone. The format of a typical four-fold (2 × 2) contingency table is shown in Table 17.4. The numbers in the table (indicated by a, b, c and d) are the numbers of patients in each treatment group that fall into each outcome category. The assumption made to formulate the null hypothesis that the treatment outcomes are the same is that the overall response rate (i.e. the total number of patients with good responses divided by the total number of patients; V1/N in Table 17.4) is the same for both treatments. Chi-square is then used to determine how likely it is that the actual numbers observed could be obtained by chance or sampling variation if the response rate for the two treatments were the same. A continuity correction in the χ2 is recommended to analyse smaller data sets (20–40 patients). This correction is used to account for the use of continuous curves to approximate the discrete frequencies in contingency tables. The Yates correction is most commonly used (Table 17.4). Chi-square should not be used to analyse small trials (trials with less than 20 patients) or when the predicted number of patients in any cell (positions a, b, c or d in Table 17.4) is less than five. In those circumstances, the Fisher exact test should be performed. Chi-square is used to analyse unpaired data and McNemar test is used to analyse paired contingency table data. Contingency table analyses can be easily modified and used to compare more than two treatments and more than two outcomes.
Table 17.4 Format of a four-fold contingency table.
| Good response | No or poor response | Total | |
| Treatment A | a | b | H1 |
| Treatment B | c | d | H2 |
| Total | V1 | V2 | N |
The χ2 for unpaired data is calculated using the formulae:
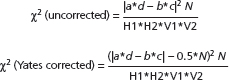
in which |a*d – b*c| indicates the absolute value of a*d – b*c.
Like the t-test, the χ2 test is frequently used incorrectly in published clinical trials. In their analysis of the use of statistics in medical papers published in the British Medical Journal, Gore et al. found that χ2 was used incorrectly in 12 of 62 published papers [5]. The errors included omission of the continuity correction for studies with few patients, omission of clearly stated hypotheses to be tested, lack of consideration of degrees of freedom and misuse of the test to study paired data.
Confidence intervals
Standard statistical hypothesis testing generally results in a determination of a P value that is the probability that a difference as large as the observed difference might arise by chance. If this probability is equal to or less than a predetermined ‘critical value’ (usually 0.05), the null hypothesis is rejected and the difference is considered statistically significant. If the P value exceeds the predetermined value, the null hypothesis is not rejected and the difference is considered not statistically significant. This dichotomous treatment of the results of clinical trials as being significant or not significant sometimes may be misleading and may hide meaningful estimates in the differences between the treatments. What matters most in a therapeutic trial is whether investigators have been able to detect a medically significant difference in treatments and how large the difference is likely to be. The conventional significance levels are useful guides to the interpretation of trial results but they should not be considered strict rules. The absurdity of the dichotomous significance testing approach is best appreciated by considering two trials, one of which has a P value of 0.05 and the other a P value of 0.06. The difference in the level of significance is very small, yet the former is considered statistically significant and the latter is not.
Reporting results with confidence intervals is an alternative or complementary way to present the results of clinical trials. Many believe it is far preferable. In simple terms, the reported result provides the best estimate of the treatment effect and the confidence interval provides a range of values in which the ‘population’ or true response to treatment lies. If the trial is repeated many times, 95% of the confidence intervals produced will contain the true or population mean response to treatment. The population or true mean has only a one in 20 chance of falling outside the 95% confidence interval. The true response rate will most probably lie near the middle of the confidence interval and will rarely be found at or near the ends of the interval. If the 95% confidence intervals around two means or medians do not overlap, you can be confident at the 95% level that the two population means or medians, from which the samples were drawn, are different.
The confidence interval provides a direct, numerical measurement of the imprecision of the estimate of the response to treatment that is due to sampling variability. The width of the confidence interval is determined by the sample size (the larger the sample, the narrower the interval), the variability of the response being measured (the larger the variability, the wider the interval) and the degree of confidence desired (the higher the confidence desired, the wider the interval) (Figure 17.8). Confidence intervals can be determined for means and their differences, and for proportions and their differences by looking them up in tables, by calculating them with formulae or by using computer software. In comparative studies, confidence intervals should be reported for the differences between groups, not for the results of each group separately.
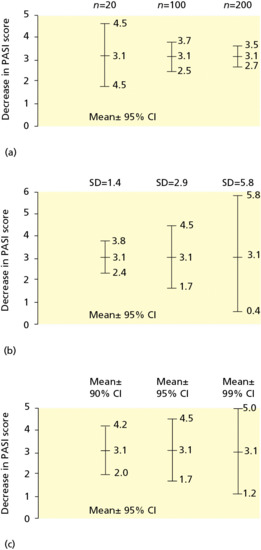
Figure 17.8 The effects of (a) sample size, (b) variability and (c) desired confidence level on confidence intervals (CIs). (a) The mean change in psoriasis area and severity index (PASI) score was 3.1 with a standard deviation (SD) of 2.9. The 95% CI is shown and narrows as the number of patients studied increases from 20 to 200. (b) The mean change in the PASI score of 20 patients was 3.1. The 95% CI is shown and widens as the sample variability (SD) increases. (c) The mean change in the PASI score of 20 patients was 3.1 with an SD of 2.9. The CI widens as the degree of confidence desired increases from 90% to 99%.
There is a close relationship between the results of a test of a hypothesis and the associated confidence interval; if the difference between treatments is significant at the 5% level, then the associated 95% confidence interval excludes the zero difference. The advantage of using confidence intervals instead of, or in addition to, P values is that confidence intervals provide an indication of the size of the differences in treatments and give numerical measurements of the inexactness in our knowledge of the real differences in treatments.
Confidence intervals can be valuable in interpreting data from trials in which the difference is not statistically significant (i.e. the P value is greater than 0.05). To determine whether a treatment effect may have been missed in a study reporting negative results one should look at the upper boundary of the 95% confidence interval. If this value would be clinically important if it were the true response, then an important treatment effect may have been missed in the study. In the calcipotriol and betamethasone trial as an example, the upper boundary of the difference in PASI scores was 0.78. This difference in PASI scores would be unlikely to have much clinical significance and therefore it is unlikely that a significant treatment advantage for calcipotriol was missed in this study.
In contrast, consider our hypothetical new treatment for metastatic melanoma that had a cure rate of 7/15 versus 3/15 for conventional treatment. The cure rate for the new treatment and conventional treatment were 47% and 20% respectively, and the difference between them was 27%. The 95% interval for the difference in proportions was –10% to 51%. The upper boundary of the difference in cure rates was 51%. This difference would clearly have a significant impact on the treatment of patients with metastatic melanoma and, therefore, a significant treatment advance may have been missed in this study. Also note that the 95% confidence interval of the difference in proportions does not exclude the zero difference; therefore, we cannot be 95% certain that the response rates of the two treatments are different.
Confidence intervals may also be useful in interpreting the response to a single treatment. Ninety-five per cent confidence intervals for the response rate of a single treatment can be determined using formulae, tables, nomograms and computer programmes. For example, suppose a physician treated 20 patients with lichen planus with metronidazole and found that 12 (60%) had an excellent response. The confidence interval for this response rate ranges from 36% to 81%. Thus the true overall response rate might well be substantially less (or more) than the physician concludes from personal experience. An important point can be made from determining the confidence interval of a single proportion. There is a degree of uncertainty in reported response rates that can be expressed in exact numerical terms by determining the confidence interval.
Confidence intervals may also be useful in interpreting the rate of side effects observed in a clinical trial. For example, in the calcipotriol study 40 out of 201 patients (20%) treated with calcipotriol developed lesional or peri-lesional irritation. The 95% confidence interval for this adverse reaction would be 14–26%. Thus a high rate of local irritation can be anticipated with calcipotriol and the rate may be as high as 26%. If no untoward reactions occur in a study, it is still possible to determine the 95% confidence interval of adverse reactions. Accurate upper 95% limits of the reaction rate can be obtained by referring to available tables. If the number exposed is at least 30, a reasonable approximation of the 95% confidence limit of the rate of adverse reactions can be obtained by dividing three by the number of patients that were exposed to the studied treatment. For example if no events occur in 100 exposed patients, the upper 95% confidence interval is 3/100 or 0.03 [7].
Power
Significant differences in treatment effects in comparison trials may be missed if the number of subjects tested is small. For example, in a 1978 survey of 71 published trials with negative results, Freiman et al. found that a 25% or 50% improvement in outcome might have been missed in 57 (80%) and 34 (48%) of the studies, respectively [8]. The importance of this observation and the importance of determining the power of studies to detect clinically significant differences in treatments are illustrated by the fact that this study has been cited more than 700 times. In spite of the recognition of the importance of power, a follow-up study conducted by Moher et al. in 1994 indicated that 25% or 50% improvements in outcome might have been missed in 84% and 64% of 102 negative studies, respectively [9].
Power is an expression of the ability of a trial to detect a difference in treatments if one exists. The investigators in a well-designed clinical trial should have an estimate or prediction of the anticipated differences between treatments, and a knowledge of the magnitude of differences that would be clinically important. The trial should then be designed to enrol a sufficient number of patients to ensure with reasonable certainty that a statistically significant difference would be obtained if the anticipated or clinically important differences between the treatments existed. The error of believing that there are no differences between treatments, when in fact there are differences, is a Type II or β error.
The power of a trial to detect a significant difference is determined by the response rates of the treatments, the significance level desired by the investigators and the number of patients treated. The power of a trial to detect differences between treatments can be calculated using formulae, nomograms, programmable calculators or computer software. Conventionally, a power of 80% with a significance level of 0.05 is considered adequate. The choice of a power of 80% means that, if the anticipated or clinically important difference in treatments really exists, four of five trials with the specified number of patients in the treatment groups will show a statistically significant difference. However, a higher power sometimes may be desirable. For example, increasing the power to 90% means that nine of 10 trials would detect a statistically significant difference between treatments if the difference really exists. The power of a study design to detect clinically significant differences in treatments is best considered before the trial is initiated. However, studies that fail to demonstrate statistically significant differences among treatments should always include a discussion of power.
The sample size needed to detect a difference is small when the difference in treatments is large. Conversely, the sample size needed to detect differences is large when the difference in treatments is small or when the response rate of the comparison treatment is high.
As noted by Moher et al. [9],
If a trial with negative results has a sufficient sample size to detect a clinically important effect, then the negative results are interpretable – the treatment did not have an effect at least as large as the effect considered to be clinically relevant. If a trial with negative results has insufficient power, a clinically important but statistically insignificant effect is usually ignored or, worse, is taken to mean that the treatment under study made no difference. Thus, there are important scientific reasons to report sample size and/or power calculations.
The importance of statistical analyses must be kept in proper perspective. Statistics are a tool for trying to ensure that results of clinical trials are not due to chance or sampling variation alone. The combination of hypothesis testing and the use of confidence intervals give a measure of the likelihood that results of a trial are due to chance and the precision of the estimated difference in treatments, respectively. Statistical analyses cannot tell you the medical significance of differences in treatments. In other words, statistically significant should not, and cannot, be equated with medically significant. Conversely, a trial whose results indicate that the difference in treatments was not statistically significant does not necessarily mean that there is not a medically important difference between treatments. It may simply mean that too few patients were used to detect the difference that does exist.
Shortcut method for appraising clinical research papers
The EBM criteria for appraising evidence represent subsets of other schemes for appraising the quality of clinical research [1]. These methods include QUOROM, PRISMA, CONSORT, Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) and the methods of DerSimonian, Evans and Pollock, Poynard, Nyberg and many others [1, 2, 10, 11, 12]. What is common to all of these methods is that they require the entire paper to be read, especially the methods section. Doing so is often not possible for busy clinicians trying to find answers to specific problems. Nor is it the most efficient use of his or her time. Instead, a shortcut method for evaluating the literature is available (Table 17.5). A shortcut method to evaluate clinical trials will enable you to use your time efficiently. It allows you to decide not to read the majority of poorly conceived, designed, executed or reported trials and those trials with insignificant results. After each step you should re-ask the questions, ‘Am I still interested in this trial?’ and ‘Is it worth spending my valuable time on it?’
Table 17.5 Shortcut method for evaluating clinical research papers.
| Step | Comments |
| Read title | If interesting, continue |
| Read abstract | If still worthy of your time, continue |
| Look at the figures and tables | Find the most important data. Are the data adequately reported? Is there a control group? Are the outcomes clinically important? Are the data subjected to statistical testing and are the tests used correctly? If still worthy of your time, continue |
| Read the results | Are complications reported? Are compliance and lost patients considered? Ask yourself ‘If everything the authors say is true, is it important for my patients, my practice or for the field of dermatology?’ If ‘no’, stop reading; if ‘yes or possibly’, continue |
| Read the methods | How were the patients chosen and allocated? Are the outcomes clearly defined and assessed blindly? Are the conclusions valid? If yes, continue |
| Record the citation | Note the authors, citation and conclusions of the study for easy retrieval later |
| Read the discussion | |
| Read the introduction |
First read the title. If the title holds interest for you, read the abstract. If after reading the abstract you still feel that the article is worthy of your time, look at the figures and tables. Authors generally display their best or most convincing data in these [13]. In a well-written study, you should be able see the important results in summary figures and tables. Try to pick out the one or two figures or tables that hold the most important data. Look at the data to see whether they are summarized and displayed correctly. Determine whether there is an appropriate control group, whether the outcomes are clinically and biologically important, whether the data are subjected to statistical analysis and whether the correct statistical methods were used. It is important that you examine and assess the data yourself. If you are still convinced that the article is worthy of your time, read the results. Determine whether complications are reported, and whether compliance and lost patients were considered. After reading the results, ask yourself the question, ‘If everything the authors say is true, is it important for my patients, for my practice or for dermatology as a whole?’ If the answer is an emphatic ‘no’, stop reading; if ‘yes or possibly’, continue to the methods.
While reading the methods pay particular attention to the features that strengthen clinical trials and help validate their conclusions. In particular, determine the eligibility criteria, whether patients were randomly allocated and whether the outcome is clearly defined and assessed masked. Make an effort to find out who paid for the study and whether all possible conflicts of interest were declared [14]. If your conclusion is that the trial was conducted in a reasonable manner and the conclusions are valid, then make some notation of who the authors are and the conclusions of the study. Several software packages for cataloguing and managing references are available for most computer platforms (e.g. EndNote® and Reference Manager®). Finally, if you still have time and interest, read the discussion and introduction, in that order.
References
Evidence-based medicine
- Bigby M, Corona R, Szklo M. Evidence-based medicine. In: Goldsmith LA, Katz SI, Gilchrest BA, Paller A, Leffell DJ, Wolff K, eds. Fitzpatrick's Dermatology in General Medicine, 8th edn. Columbus, OH: McGraw-Hill, 2012:9–15.
- Anonymous. Medical research council streptomycin in tuberculosis trials committee. Streptomycin treatment of pulmonary tuberculosis. BMJ 1948;ii:769–82.
- Cochrane A. Effectiveness and Efficiency. Random Reflections on Health Services. London: Nuffield Provincial Hospital Trust, 1972.
- Sackett DL, Haynes RB, Guyatt GH, Tugwell P. Clinical Epidemiology: A Basic Science for Clinical Medicine. Boston: Little, Brown and Company, 1991.
- Evidence Based Medicine Working Group. Evidence-based medicine a new approach to teaching the practice of medicine. JAMA 1992;268:2420–5.
- Sackett DL, Rosenberg WM, Gray JA, Haynes RB, Richardson WS. Evidence based medicine: what it is and what it isn't. BMJ 1996;312:71–2.
- Chalmers I, Dickersin K, Chalmers TC. Getting to grips with Archie Cochrane's agenda. BMJ 1992;305:786–8.
- Strauss SR, Sackett DL. Bringing evidence to the clinic. Arch Dermatol 1998;134:1519–20.
- Covell DG, Uman GC, Manning PR. Information needs in office practice: are they being met? Ann Intern Med 1985;103:596–9.
- Arndt K. Information excess in medicine. Overview, relevance to dermatology, and strategies for coping. Arch Dermatol 1992;128:1249–56.
- Williams HC. Dowling Oration 2001. Evidence-based dermatology 2 a bridge too far? Clin Exp Dermatol 2001;26:714–24.
- Sterne JA, Egger M, Smith GD. Systematic reviews in health care: investigating and dealing with publication and other biases in meta-analysis. BMJ 2001;323:101—5.
- Katz KA, Swetman GL. Imiquimod, molluscum, and the need for a better “Best Pharmaceuticals for Children” act. Pediatrics 2013;132:1–3.
- Bigby M, Stern RS, Bigby J. An evaluation of method reporting and use in clinical trials in dermatology. Arch Dermatol 1985;121:1394–9.
- Adetugbo K, Williams H. How well are randomized controlled trials reported in the dermatology literature? Arch Dermatol 2000;136:381–5.
- Hu SW, Bigby M. Pityriasis versicolor: a systematic review of interventions. Arch Dermatol 2010;146:1132–40.
- Parker ER, Schilling LM, Diba V, Williams HC, Dellavalle RP. What is the point of databases of reviews for dermatology if all they compile is “insufficient evidence”? J Am Acad Dermatol 2004;50:635–9.
- Lexchin J, Bero LA, Djulbegovic B, Clark O. Pharmaceutical industry sponsorship and research outcome and quality: systematic review. BMJ 2003:326:1167–70.
- Boutron I, Dutton S, Ravaud P, Altman DG. Reporting and interpretation of randomized controlled trials with statistically nonsignificant results for primary outcomes. JAMA 2010;303:2058–64.
- Nankervis H, Baibergenova A, Williams HC, Thomas KS. Prospective registration and outcome-reporting bias in randomized controlled trials of eczema treatments: a systematic review. J Invest Dermatol 2012;132:2727–34.
- Sackett DL. Surveys of self-reported reading times of consultants in Oxford, Birmingham, Milton-Keynes, Bristol, Leicester, and Glasgow. In: RosenbergWMC, RichardsonWS, HaynesRB, SackettDL, eds. Evidence-based Medicine. London: Churchill Livingstone, 1997:1–20.
Formulating questions and finding evidence
- Rzany B, Bigby M. Formulating well built clinical questions. In: Williams HC, Bigby M, Diepgen T, Herxheimer A, Naldi L, Rzany B, eds. Evidence-based Dermatology, 2nd edn. London: BMJ Books, 2009:29–30.
- Guyatt G, Drummond R, Meade M, Cook D. The Evidence Based Medicine Working Group Users’ Guides to the Medical Literature, 2nd edn. Chicago: McGraw Hill, 2008:17–28.
- Riva JJ, Malik KM, Burnie SJ, Endicott AR, Busse JW. What is your research question? An introduction to the PICOT format for clinicians. J Can Chiropr Assoc 2012;56:167–71.
- Bigby M, Corona R, Szklo M. Evidence-based Medicine. In: Goldsmith LA, Katz SI, Gilchrest BA, Paller A, Leffell DJ, Wolff K, eds. Fitzpatrick's Dermatology in General Medicine, 8th edn. Columbus, OH: McGraw-Hill, 2012:9–15.
- Bigby M. Challenges to the hierarchy of evidence: does the emperor have no clothes? Arch Dermatol 2001;137:345–6.
- Lau J, Antman EM, Jimenez-Silva J, Kupelnick B, Mosteller F, Chalmers TC. Cumulative meta-analysis of therapeutic trials for myocardial infarction [see comments]. N Eng J Med 1992;327:248–54.
- LeLorier J, Gregoire G, Benhaddad A, Lapierre J, Derderian F. Discrepancies between meta-analyses and subsequent large randomized, controlled trials. N Engl J Med 1997;337:536–42.
- Lau J, Ionnidis JPA, Schmid CH. Summing up evidence: one answer is not always enough. Lancet 1998;351:123–7.
- Kunz R, Oxman AD. The unpredictability paradox: review of empirical comparisons of randomised and non-randomised clinical trials. BMJ 1998;317:1185–90.
- Benson K, Hartz AJ. A comparison of observational studies and randomized, controlled trials. N Engl J Med 2000;342:1878–86.
- Concato J, Shah N, Horwitz R. Randomized, controlled trials, observational studies, and the hierarchy of research design. N Engl J Med 2000;342:1887–92.
- Williams HC, Dellavalle RP. The growth of clinical trials and systematic reviews in informing dermatological patient care. J Invest Dermatol 2012;132:1008–17.
- Nisbett R, Ross L. Human Inference: Strategies and Shortcomings of Social Judgment. Englewood Cliffs, NJ: Prentice-Hall, 1980.
- Bigby M. Paradigm lost. Arch Dermatol 2000;136:26–7.
- Wolkenstein P, Latarjet J, Roujeau JC, et al. Randomised comparison of thalidomide versus placebo in toxic epidermal necrolysis. Lancet 1998;352:1586–9.
- Collier A, Heilig L, Schilling L, Williams H, Dellavalle RP. Cochrane Skin Group systematic reviews are more methodologically rigorous than other systematic reviews in dermatology. Br J Dermatol 2006;155:1230–5.
- Reddi A, Prescott L, Doney E, et al. The Cochrane Skin Group: a vanguard for developing and promoting evidence-based dermatology. J Evid Based Med 2013;6:236–42.
- Adetugbo K, Williams H. How well are randomized controlled trials reported in the dermatology literature? Arch Dermatol 2000;136:381–5.
- Spuls PI, Witkamp L, Bossuyt PM, Bos JD. A systematic review of five systemic treatments for severe psoriasis. Br J Dermatol 1997;137:943–9.
- Greenhalgh T. How to Read a Paper: the Basics of Evidence Based Medicine, 5th edn. London: BMJ Publishing Group, 1997.
- Anders ME, Evans DP. Comparison of PubMed and Google Scholar Literature Searches. Respir Care 2010;55(5):578–83.
- Schultz M. Comparing test searches in PubMed and Google Scholar J Med Libr Assoc 2007;95(4):442–5.
- Freeman MK, Lauderdale SA, Kendrach MG, Woolley TW. Google Scholar versus PubMed in locating primary literature to answer drug-related questions. Ann Pharmacother 2009;43(3):478–84.
- Nankervis H, Maplethorpe A, Williams HC. Mapping randomised controlled trials of treatments for eczema – the GREAT database. BMC Dermatol 2011;11:10.
Critically appraising evidence and applying it to individual patients
- Bigby M, Corona R, Szklo M. Evidence-based medicine. In: Goldsmith LA, Katz SI, Gilchrest BA, Paller A, Leffell DJ, Wolff K, eds. Fitzpatrick's Dermatology in General Medicine, 8th edn. Columbus, OH: McGraw-Hill, 2012:9–15.
- Bigby M. Understanding and evaluating systematic reviews. Indian J Dermatol 2014;59:134–9.
- Moher D, Liberati A, Tetzlaff J, Altman DG, PRISMA Group. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: the PRISMA Statement. BMJ 2009;339:b2535.
- Egger M, Smith GD, Sterne JA. Uses and abuses of meta-analysis. Clin Med 2001;1:478–84.
- HigginsJPT, GreenS, eds. Cochrane Handbook for Systematic Reviews of Interventions, Version 5.1.0 (updated March 2011), www.handbook.cochrane.org (last accessed May 2014).
- HigginsJPT, GreenS, eds. Cochrane Handbook for Systematic Reviews of Interventions, Version 5.1.0 (updated March 2011), http://handbook.cochrane.org (last accessed May 2014).
- Cochrane Collaboration. Cochrane Collaboration's tool for assessing risk of bias. http://ohg.cochrane.org/sites/ohg.cochrane.org/files/uploads/Risk%20of%20bias%20assessment%20tool.pdf (last accessed May 2014).
- Sterne JA, Egger M, Smith GD. Systematic reviews in health care: investigating and dealing with publication and other biases in meta-analysis. BMJ 2001;323:101–5.
- Dickersin K, Min YI, Meinert CL. Factors influencing publication of research results. Follow-up of applications submitted to two institutional review boards. JAMA 1992;267:374–8.
- Katz KA, Swetman GL. Imiquimod, molluscum, and the need for a better “best pharmaceuticals for children” act. Pediatrics 2013;132(1):1–3.
- Goldacre B. Bad science. http://www.badscience.net/category/publication-bias/ (last accessed May 2014).
- Jorgensen AW, Hilden J, Gotzsche PC. Cochrane reviews compared with industry supported meta-analyses and other meta-analyses of the same drugs: systematic review. BMJ 2006;333:782.
- Collier A, Heilig L, Schilling L, Williams H, Dellavalle RP. Cochrane Skin Group systematic reviews are more methodologically rigorous than other systematic reviews in dermatology. Br J Dermatol 2006;155:1230–5.
- Olsen O, Middleton P, Ezzo J, et al. Quality of Cochrane reviews: assessment of sample from 1998. BMJ 2001;323:829–32.
- Abuabara K, Freeman EE, Dellavalle R. The role of systematic reviews and meta-analysis in dermatology. J Invest Dermatol 2012;132(11):e2.
- Schriger DL, Altman DG, Vetter JA, Heafner T, Moher D. Forest plots in reports of systematic reviews: a cross-sectional study reviewing current practice. Int J Epidemiol 2010;39:421–9.
- Katz KA. The (relative) risks of using odds ratios. Arch Dermatol 2006;142:761–4.
- Centre for Evidence Based Medicine. Number needed to treat. http://www.cebm.net/index.aspx?o=1044 (last accessed May 2014).
- StatTools.net. http://www.statstodo.com/RiskOddsConv_Pgm.php (last accessed May 2014).
- Manriquez JJ, Villouta MF, Williams HC. Evidence-based dermatology: number needed to treat and its relation to other risk measures. J Am Acad Dermatol 2007;56:664–71.
- HigginsJPT, GreenS, eds. Cochrane Handbook for Systematic Reviews of Interventions, Version 5.1.0 (updated March 2011), chapter 9.5. www.handbook-cochrane.org (last accessed May 2014).
- Macaskill P, Walter SD, Irwig L. A comparison of methods to detect publication bias in meta-analysis. Stat Med 2001;20:641–54.
- Parker ER, Schilling LM, Diba V, Williams HC, Dellavalle RP. What is the point of databases of reviews for dermatology if all they compile is “insufficient evidence”? J Am Acad Dermatol 2004;50:635–9.
- González U, Whitton M, Eleftheriadou V, Pinart M, Batchelor J, Leonardi-Bee J. Guidelines for designing and reporting clinical trials in vitiligo. Arch Dermatol 2011;147:1428–36.
- Bigby M, Gadenne A-S. Understanding and evaluating clinical trials. J Am Acad Dermatol 1996;34:555–90.
- Williams HC. How to critically appraise a randomized controlled trial. In: Williams HC, Bigby M, Diepgen T, Herxheimer A, Naldi L, Rzany B, eds. Evidence-based Dermatology, 2nd edn. London: BMJ Books, 2008:44–51.
- Guillaume J-C, Vaillant L, Bernard P, et al. Controlled trial of azathioprine and plasma exchange in addition to prednisolone in the treatment of bullous pemphigoid. Arch Dermatol 1993;129:49–53.
- Kirtschig G, Middleton P, Bennett C, Murrell DF, Wojnarowska F, Khumalo NP. Interventions for bullous pemphigoid. Cochrane Database Syst Rev 2010;Issue 10:CD002292
- Fergusson D, Aaron SD, Guyatt G, Hebert P. Post-randomisation exclusions: the intention to treat principle and excluding patients from analysis. BMJ 2002;325:652–4.
- Allen AM. Clinical trials in dermatology. Part 3: Measuring responses to treatment. Int J of Dermatol 1980;19:1–6.
- Fredriksson T, Pettersson U. Severe psoriasis-oral therapy with a new retinoid. Dermatologica 1978;157:238–44.
- Tiling-Grosse S, Rees J. Assessment of area of involvement in skin disease: a study using schematic figure outlines. Br J Dermatol 1992;128:69–74.
- Schmitt J, Langan S, Stamm T, Williams H on behalf of the Harmonizing Outcome Measurements in Eczema (HOME) Delphi Panel. Core outcome domains for controlled trials and clinical recordkeeping in eczema: international multi-perspective Delphi consensus process. J Invest Dermatol 2011;131:623–30.
- Whitley R, Weiss H, Gann J, et al. Acyclovir with and without prednisone for the treatment of herpes zoster. Ann Intern Med 1996;125:376–83.
- Freiman JA, Chalmers TC, Smith JH, Kuebler RR. The importance of beta, the type II error and sample size in the design and interpretation of the randomized control trial. N Eng J Med 1978;299:690–4.
- Moher D, Dulberg CS, Wells GA. Statistical power, sample size, and their reporting in randomized controlled trials. JAMA 1994;272:122–4.
- Williams HC, Seed P. Inadequate size of ‘negative’ clinical trials in dermatology. Br J Dermatol 1993;128:317–26.
- Bigby M. Ruling out the diagnosis. Arch Dermatol 1996;132:697–8.
- Ferrante di Ruffano L, Hyde CJ, McCaffery KJ, Bossuyt PM, Deeks JJ. Assessing the value of diagnostic tests: a framework for designing and evaluating trials. BMJ 2012;344:e686.
- Dolman GE, Nieboer D, Steyerberg EW, et al. The performance of transient elastography compared to clinical acumen and routine tests – what is the incremental diagnostic value? Liver Int 2013;33:172–9.
- Bossuyt PM, Reitsma JB, Bruns DE, et al. Towards complete and accurate reporting of studies of diagnostic accuracy: the STARD initiative. BMJ 2003;326:41–4.
- Thygesen LC, Andersen GS, Andersen H. A philosophical analysis of the Hill criteria. J Epidemiol Community Health 2005;59:512–16.
- Wolf P, Quehenberger F, Mullegger R, Stranz B, Kerl H. Phenotypic markers, sunlight-related factors and sunscreen use in patients with cutaneous melanoma: an Austrian case–control study. Melanoma Res 1998;8:370–8.
- Ashcroft DM, Dimmock P, Garside R, Stein K, Williams HC. Efficacy and tolerability of topical pimecrolimus and tacrolimus in the treatment of atopic dermatitis: meta-analysis of randomised controlled trials. BMJ 2005;330:516–25.
- Sackett D, Richardson W, Rosenberg W, Haynes R. Evidence-based Medicine: How to Practice and Teach EBM. Edinburgh: Churchill Livingstone, 1996.
Evaluating the data in clinical research papers and a shortcut method for reading clinical research papers
- Bigby M, Gadenne A-S. Understanding and evaluating clinical trials. J Am Acad Dermatol 1996;34:555–90.
- Moher D, Liberati A, Tetzlaff J, Altman DG, PRISMA Group. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: the PRISMA Statement. BMJ 2009;339:b2535.
- Bland JM, Bland DG. Statistics notes: one and two sided tests of significance. BMJ 1994;309:248.
- Cunliffe WJ, Berth-Jones J, Claudy A, et al. Comparative study of calcipotriol (MC 903) ointment and betamethasone 17-valerate ointment in patients with psoriasis vulgaris. J Am Acad Dermatol 1992;26:736–43.
- Gore SM, Jones IG, Rytter EC. Misuse of statistical methods: critical assessment of articles in BMJ from January to March 1976. BMJ 1977;1(6053):85-7.
- Glantz SA. Current topics biostatistics: how to detect, correct and prevent errors in the medical literature. Circulation 1980;61:1–7.
- Eypasch E, Lefering R, Kum CK, Troidl H. Probability of adverse events that have not yet occurred: a statistical reminder. BMJ 1995;311:619–20.
- Freiman JA, Chalmers TC, Smith J, et al. The importance of beta, the Type II error and sample size in the design and interpretation of the randomized control trial. N Eng J Med 1978;299:690–4.
- Moher D, Dulberg CS, Wells GA. Statistical power, sample size, and their reporting in randomized controlled trials. JAMA 1994;272:122–4.
- Moher D, Cook DJ, Eastwood S, Olkin I, Rennie D, Stroup DF. Improving the quality of reports of meta-analyses of randomised controlled trials: the QUOROM statement. Quality of Reporting of Meta-analyses. Lancet 1999;354:1896–900.
- Moher D, Hopewell S, Schulz KF, et al. CONSORT 2010 explanation and elaboration: updated guidelines for reporting parallel group randomised trials. BMJ 2010;340:c869.
- Von Elm E, Altman DG, Egger M, Pocock SJ, Gotzsche PC, Vandenbroucke JP; STROBE Initiative. Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) statement: guidelines for reporting observational studies. BMJ 2007;335:806–8.
- Murray GD. Statistical guidelines for the British Journal of Surgery. Br J Surg 1991;78:782–4.
- Williams HC, Naldi L, Paul C, Vahlquist A, Schroter S, Jobling R. Conflicts of interest in dermatology. Acta Derm Venereol 2006;86(6):485–97.