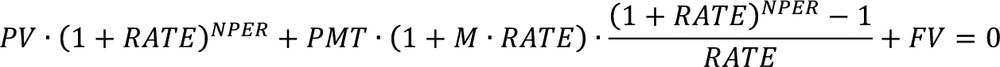Syntax. NPER(Rate,Pmt,Pv,Fv,Type)
Definition. The function NPER() calculates the duration of a compound interest rate process, annuity calculation, or repayment calculation. It is based on possible regular payments of the same amount and/or one-time payments at the start or end of the time period, according to the finance mathematical benefit principle
Payment of the creditor + Payment of the debtor = 0
Arguments
Rate (required) The (constant) period interest rate as interest rate in arrears.
Pmt (required/optional, see Note) The amount of the regular payments. This can be interpreted as annuity.
Pv (required/optional, see Note) The start value of one payment direction. For disbursement plans, this is the account balance at the beginning of these considerations; for repayment plans, it is the loan amount.
Fv (optional/required, see Note) The account balance you want to have at the end of the process (for example, a residual balance from disbursement plans or a final repayment in the amount of the residual debt for loans).
Type (optional) Specifies whether regular payments take place at the end of the periods (Type = 0 or not specified) or at the start of the periods (Type = 1).
Note
At least two of the three arguments Pmt, Pv, and Fv must be specified and must not be zero. Their sign corresponds to the respective “direction of the money flow” (compare to the complex formula in the background section for this function).
Important
The finance mathematical benefit principle means that you need to differentiate between disbursements and deposits in regard to the leading sign (borrowing and repayment, investment and disinvestment). Here Excel differs from the benefit principle used in finance mathematical literature:
Payment of the creditor = Payment of the debtor
Background. The five functions PV() = cash value, FV() = future value, PMT() = regular payment, NPER() = interest or payment time periods, and RATE() = interest rate, have the following relationship when the benefit principle is implemented:
where M is the Type (timing of payments).
The cash value interest is compounded, and so are the regular payments. At the end, the sum is compared to the future value.
Using one of these functions is equal to the respective basic finance mathematical task: calculation of an unknown variable from the preceding equation, when the other variables are known. The functions solve the equation for each of its members. For RATE, an approximation calculation is performed.
Note
Interest rates are usually specified as annual interest rates. These functions work correctly only if the periods match the interest rate. With intra-annual interest yield, the annual interest rate is usually distributed equally over the periods: 12 months at one twelfth of the interest rate, 3 months at a quarter, and half a year at half.
Examples. The headings of the following examples reflect the general usage of finance mathematical terms.
Compound Interest Calculation. An investor wants to have a small financial cushion for retirement and decides to invest a newly received inheritance of $10,000.00 at a fixed interest rate of 4.5 percent. He hopes to get a disbursement of at least $25,000.00. How long does he need to leave the money in the bank?
A calculation with
=NPER(4.5%,,-10000,25000)
returns 20.82 years. This means that at the end of the 20th year the target has not been reached, but at the end of the 21st year it has been passed. The concrete account balances can be calculated with the numbers 20 or 21 for the duration argument by using FV(). Alternatively, you can use an account plan.
Annuity calculation. A 60-year-old has saved $100,000.00 and would like to be paid an additional monthly annuity of $750.00. Is the saved money enough, if 4.5 percent p.a. is paid on top of the existing balance?
You determine the cash value of the annuity with
=NPER(4.5%/12,-750,100000,,1)
to get the result of 184.19 months. This means that at the end of the 184th month, the account has been reduced so much that no further withdrawal can be made.
The calculation is based on compound interest within one year. Because compound interest cannot be used for a regular savings account, the result remains only theoretical.
Repayment Calculation (Annuity Repayment). A debtor is able to pay back $1,000.00 per month on a loan (repayment plus interest). The interest rate for the duration is 5.5 percent. How long does the loan have to be paid back, if the amount of loan is $175,000.00?
NPER() can be used here as well (in this case, the repayment calculation is the annuity calculation). You are using the following to get to a result of 354.24 months:
=NPER(5.5%/12,-1000,175000)
Therefore, the final payment takes place in the 355th month, and it is smaller than the regular payment.
Note
This example shows that Excel can also handle percentage annuities in the repayment calculation. For those, the repayment amount can be calculated not from the duration (see PMT()) but by displaying the repayment rate that determines the first repayment rate. The sum of the first repayment rate and the interest of the first period is then the regular repayment amount.
Unlike a savings account, a mortgage loan uses a monthly interest of a twelfth of the agreed-upon yearly interest rate (nominal interest).
Important
Using formulas may be different from keeping detailed notes of an account history with deposits and withdrawals because of rounding errors. This happens because the numbers for a savings account are rounded to two decimal places. If you are recreating such an account with Excel, you should use the function ROUND() for intermediary steps that involve money. Simply limiting the display of the cell value to two decimal places often leads to incorrect results.