§ 9.

The concepts form a peculiar class, existing only in the mind of man, and differing entirely from the representations of perception so far considered. Therefore we can never attain to a perceptive, a really evident knowledge of their nature, but only to an abstract and discursive one. It would therefore be absurd to demand that they should be demonstrated in experience, in so far as we understand by this the real external world that is simply representation of perception, or that they should be brought before the eyes or the imagination like objects of perception. They can only be conceived, not perceived, and only the effects that man produces through them are objects of experience proper. Such effects are language, deliberate and planned action and science, and what results from all these. As object of external experience, speech is obviously nothing but a very complete telegraph communicating arbitrary signs with the greatest rapidity and the finest difference of shades of meaning. But what do these signs mean? How are they. interpreted? While another person is speaking, do we at once translate his speech into pictures of the imagination that instantaneously flash upon us and are arranged, linked, formed, and coloured according to the words that stream forth, and to their grammatical inflexions? What a tumult there would be in our heads while we listened to a speech or read a book! This is not what happens at all. The meaning of the speech is immediately grasped, accurately and clearly apprehended, without as a rule any conceptions of fancy being mixed up with it. It is reason speaking to reason that keeps within its province, and what it communicates and receives are abstract concepts, non-perceptive representations, formed once for all and relatively few in number, but nevertheless embracing, containing, and representing all the innumerable objects of the actual world. From this alone is to be explained the fact that an animal can never speak and comprehend, although it has in common with us the organs of speech, and also the representations of perception. But just because words express this quite peculiar class of representations, whose subjective correlative is reason, they are for the animal without sense and meaning. Thus language, like every other phenomenon that we ascribe to reason, and like everything that distinguishes man from the animal, is to be explained by this one simple thing as its source, namely concepts, representations that are abstract not perceptive, universal not individual in time and space. Only in single cases do we pass from concepts to perception, or form phantasms as representatives of concepts in perception, to which, however, they are never adequate. These have been specially discussed in the essay On the Principle of Sufficient Reason (§28), and so I will not repeat this here. What is there said can be compared with what Hume says in the twelfth of his Philosophical Essays (p. 244), and Herder in the Metacritic—otherwise a bad book (Part I, p. 274). The Platonic Idea that becomes possible through the union of imagination and reason is the main subject of the third book of the present work.

Now although concepts are fundamentally different from representations of perception, they stand in a necessary relation to them, and without this they would be nothing. This relation consequently constitutes their whole nature and existence. Reflection is necessarily the copy or repetition of the originally presented world of perception, though a copy of quite a special kind in a completely heterogeneous material. Concepts, therefore, can quite appropriately be called representations of representations. Here too the principle of sufficient reason has a special form. The form under which the principle of sufficient reason rules in a class of representations also always constitutes and exhausts the whole nature of this class, in so far as they are representations, so that, as we have seen, time is throughout succession and nothing else, space is throughout position and nothing else, matter is throughout causality and nothing else. In the same way, the whole nature of concepts, or of the class of abstract representations, consists only in the relation expressed in them by the principle of sufficient reason. As this is the relation to the ground of knowledge, the abstract representation has its whole nature simply and solely in its relation to another representation that is its ground of knowledge. Now this of course can again be a concept or an abstract representation in the first instance, and even this again may have only such an abstract ground of knowledge. However, this does not go on ad infinitum, but the series of grounds of knowledge must end at last with a concept which has its ground in knowledge of perception. For the whole world of reflection rests on the world of perception as its ground of knowledge. Therefore the class of abstract representations is distinguished from the others, for in the latter the principle of sufficient reason always requires only a relation to another representation of the same class, but in the case of abstract representations it requires in the end a relation to a representation from another class.

Those concepts which, as just mentioned, are related to knowledge of perception not directly, but only through the medium of one or even several other concepts, have been called by preference abstracta, and on the other hand those which have their ground directly in the world of perception have been called concreta. This last name, however, fits the concepts denoted by it only in quite a figurative way, for even these too are always abstracta, and in no way representations of perception. These names have originated only from a very indistinct awareness of the difference they indicate; yet they can remain, with the explanation given here. Examples of the first kind, and hence abstracta in the fullest sense, are concepts such as “relation,” “virtue,” “investigation,” “beginning,” and so on. Examples of the latter kind, or those figuratively called concreta, are the concepts “man,” “stone,” “horse,” and so on. If it were not somewhat too pictorial a simile, and thus one that verges on the facetious, the latter might very appropriately be called the ground floor and the former the upper storeys of the edifice of reflection.27

It is not, as is often said to be the case, an essential characteristic of a concept that it includes much under it, in other words, that many representations of perception, or even abstract representations, stand to it in the relation of ground of knowledge, that is to say, are thought through it. This is only a derived and secondary characteristic of a concept, and does not always exist in fact, although it must always do so potentially. This characteristic arises from the fact that the concept is a representation of a representation, in other words, has its whole nature only in its relation to another representation. But as it is not this representation itself, the latter indeed frequently belonging to quite a different class of representations, in other words, being of perception, it can have temporal, spatial, and other determinations, and in general many more relations that are not thought in the concept at all. Thus several representations differing in unessential points can be thought through the same concept, that is to say, subsumed under it. But this power of embracing several things is not an essential characteristic of the concept, but only an accidental one. Thus there can be concepts through which only a single real object is thought, but which are nevertheless abstract and general representations, and by no means particular representations of perception. Such, for example, is the concept one has of a definite town, known to one only from geography. Although this one town alone is thought through it, yet there might possibly be several towns differing in a few particulars, to all of which it is suited. Thus a concept has generality not because it is abstracted from several objects, but conversely because generality, that is to say, non-determination of the particular, is essential to the concept as abstract representation of reason; different things can be thought through the same concept.

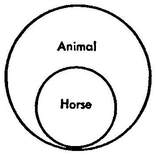
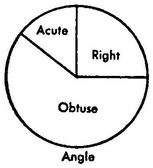
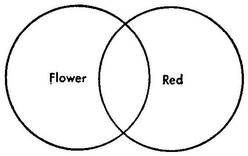
From what has been said it follows that every concept, just because it is abstract representation, not representation of perception, and therefore not a completely definite representation, has what is called a range, an extension, or a sphere, even in the case where only a single real object corresponding to it exists. We usually find that the sphere of any concept has something in common with the spheres of others, that is to say, partly the same thing is thought in it which is thought in those others, and conversely in those others again partly the same thing is thought which is thought in the first concept; although, if they are really different concepts, each, or at any rate one of the two, contains something the other does not. In this relation every subject stands to its predicate. To recognize this relation means to judge. The presentation of these spheres by figures in space is an exceedingly happy idea. Gottfried Ploucquet, who had it first, used squares for the purpose. Lambert, after him, made use of simple lines placed one under another. Euler first carried out the idea completely with circles. On what this exact analogy between the relations of concepts and those of figures in space ultimately rests, I am unable to say. For logic, however, it is a very fortunate circumstance that all the relations of concepts can be made plain in perception, even according to their possibility, i.e., a priori, through such figures in the following way:

(1) The spheres of two concepts are equal in all respects, for example, the concept of necessity and the concept of following from a given ground or reason; in the same way, the concept of Ruminantia and that of Bisulca (ruminating and cloven-hoofed animals); likewise + that of vertebrates and that of red-blooded animals (though there might be some objection to this by reason of the Annelida) : these are convertible concepts. Such concepts, then, are represented by a single circle that indicates either the one or the other.

(2) The sphere of one concept wholly includes that of another:

(3) A sphere includes two or several which exclude one another, and at the same time fill the sphere:

(4) Two spheres include each a part of the other:

(5) Two spheres lie within a third, yet do not fill it:

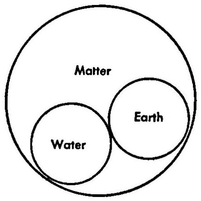
This last case applies to all concepts whose spheres have nothing immediately in common, for a third one, although often very wide, will include both.

All combinations of concepts may be referred to these cases, and from them can be derived the whole theory of judgements, of their conversion, contraposition, reciprocation, disjunction (this according to the third figure). From them may also be derived the properties of judgements, on which Kant based the pretended categories of the understanding, though with the exception of the hypothetical form, which is not a combination of mere concepts, but of judgements; and with the exception of modality, of which the Appendix gives a detailed account, as it does of all the properties of judgements that are the basis of the categories. Of the possible concept-combinations mentioned it has further to be remarked that they can also be combined with one another in many ways, e.g., the fourth figure with the second. Only if one sphere which wholly or partly contains another is in turn included wholly or partly within a third, do these together represent the syllogism in the first figure, that is to say, that combination of judgements by which it is known that a concept wholly or partly contained in another is also contained in a third, which in turn contains the first. Also the converse of this, the negation, whose pictorial representation can, of course, consist only in the two connected spheres not lying within a third sphere. If many spheres are brought together in this way, there arise long chains of syllogisms. This schematism of concepts, which has been fairly well explained in several textbooks, can be used as the basis of the theory of judgements, as also of the whole syllogistic theory, and in this way the discussion of both becomes very easy and simple. For all the rules of this theory can be seen from it according to their origin, and can be deduced and explained. But it is not necessary to load the memory with these rules, for logic can never be of practical use, but only of theoretical interest for philosophy. For although it might be said that logic is related to rational thinking as thorough-bass is to music, and also as ethics is to virtue, if we take it less precisely, or as aesthetics is to art, it must be borne in mind that no one ever became an artist by studying aesthetics, that a noble character was never formed by a study of ethics, that men composed correctly and beautifully long before Rameau, and that we do not need to be masters of thorough-bass in order to detect discords. Just as little do we need to know logic in order to avoid being deceived by false conclusions. But it must be conceded that thorough-bass is of great use in the practice of musical composition, although not for musical criticism. Aesthetics and ethics also, though in a much less degree, may have some use in practice, though a mainly negative one, and hence they too cannot be denied all practical value; but of logic not even this much can be conceded. It is merely knowing in the abstract what everyone knows in the concrete. Therefore we no more need to call in the aid of logical rules in order to construct a correct argument, than to do so to guard against agreeing with a false one. Even the most learned logician lays these rules altogether aside in his actual thinking. This is to be explained as follows. Every science consists of a system of general, and consequently abstract, truths, laws, and rules referring to some species of objects. The particular case which subsequently occurs under these laws is then determined each time in accordance with this universal knowledge that is valid once for all, because such application of the universal is infinitely easier than investigation from the very beginning of each individual case as it occurs. The universal abstract knowledge, once gained, is always nearer at hand than the empirical investigation of the particular thing. But with logic it is just the reverse. It is the universal knowledge of the reason’s method of procedure, expressed in the form of rules. Such knowledge is reached by self-observation of the faculty of reason, and abstraction from all content. But that method of procedure is necessary and essential to reason; hence reason will not in any case depart from it, the moment it is left to itself. It is therefore easier and more certain to let reason proceed according to its nature in each particular case, than to hold before it knowledge of that case which is first abstracted from this procedure in the form of a foreign law given from outside. It is easier because, although in all the other sciences the universal rule is more within our reach than is the investigation of the particular case taken by itself, with the use of reason, on the contrary, its necessary procedure in the given case is always more within our reach than is the universal rule abstracted from it; for that which thinks within us is indeed this very faculty of reason itself. It is surer, because it is easier for an error to occur in such abstract knowledge or in its application than for a process of reason to take place which would run contrary to its essence and nature. Hence arises the strange fact that, whereas in other sciences we test the truth of the particular case by the rule, in logic, on the contrary, the rule must always be tested by the particular case. Even the most practised logician, if he notices that in a particular case he concludes otherwise than as stated by the rule, will always look for a mistake in the rule rather than in the conclusion he actually draws. To seek to make practical use of logic would therefore mean to seek to derive with unspeakable trouble from universal rules what is immediately known to us with the greatest certainty in the particular case. It is just as if a man were to consult mechanics with regard to his movements, or physiology with regard to his digestion; and one who has learnt logic for practical purposes is like a man who should seek to train a beaver to build its lodge. Logic is therefore without practical use; nevertheless it must be retained, because it has philosophical interest as special knowledge of the organization and action of the faculty of reason. It is rightly regarded as an exclusive, self-subsisting, self-contained, finished, and perfectly safe branch of knowledge, to be scientifically treated by itself alone and independently of everything else, and also to be taught at the universities. But it has its real value first in the continuity of philosophy as a whole with the consideration of knowledge, indeed of rational or abstract knowledge. Accordingly, the exposition of logic should not so much take the form of a science directed to what is practical, and should not contain merely bare rules laid down for the conversion of judgements, syllogisms, and so on, but should rather be directed to our knowing the nature of the faculty of reason and of the concept, and to our considering in detail the principle of sufficient reason of knowledge. For logic is a mere paraphrase of this principle, and is in fact really only for the case where the ground that gives truth to judgements is not empirical or metaphysical, but logical or metalogical. Therefore with the principle of sufficient reason of knowing must be mentioned the three remaining fundamental laws of thought, or judgements of metalogical truth, so closely related to it, out of which the whole technical science of the faculty of reason gradually grows. The nature of thought proper, that is to say, of the judgement and syllogism, can be shown from the combination of the concept-spheres according to the spatial schema in the way above mentioned, and from this all the rules of the judgement and syllogism can be deduced by construction. The only practical use we can make of logic is in an argument, when we do not so much demonstrate to our opponent his actual false conclusions as his intentionally false ones, through calling them by their technical names. By thus pushing the practical tendency into the background, and stressing the connexion of logic with the whole of philosophy as one of its chapters, knowledge of it should not become less prevalent than it is now. For at the present time everyone who does not wish to remain generally uncultured or to be reckoned one of the ignorant and dull mob, must have studied speculative philosophy. For this nineteenth century is a philosophical one; though by this we do not mean that it possesses philosophy or that philosophy prevails in it, but rather that it is ripe for philosophy and is therefore absolutely in need of it. This is a sign of a high degree of refinement, indeed a fixed point on the scale of the culture of the times.²⁸

However little practical use logic may have, it cannot be denied that it was invented for practical purposes. I explain its origin in the following way. As the pleasure of debate developed more and more among the Eleatics, the Megarics, and the Sophists, and gradually became almost a passion, the confusion in which nearly every debate ended was bound to make them feel the necessity for a method of procedure as a guide, and for this a scientific dialectic had to be sought. The first thing that had to be observed was that the two disputing parties must always be agreed on some proposition to which the points in dispute were to be referred. The beginning of the methodical procedure consisted in formally stating as such these propositions jointly acknowledged, and putting them at the head of the inquiry. These propositions were at first concerned only with the material of the inquiry. It was soon observed that, even in the way in which the debaters went back to the jointly acknowledged truth, and sought to deduce their assertions from it, certain forms and laws were followed, about which, although without any previous agreement, there was never any dispute. From this it was seen that these must be the peculiar and essentially natural method of reason itself, the formal way of investigating. Now although this was not exposed to doubt and disagreement, some mind, systematic to the point of pedantry, nevertheless hit upon the idea that it would look fine, and would be the completion of methodical dialectic, if this formal part of all debating, this procedure of reason itself always conforming to law, were also expressed in abstract propositions. These would then be put at the head of the inquiry, just like those propositions jointly acknowledged and concerned with the material of the inquiry, as the fixed canon of debate, to which it would always be necessary to look back and to refer. In this way, what had hitherto been followed as if by tacit agreement or practised by instinct would be consciously recognized as law, and given formal expression. Gradually, more or less perfect expressions for logical principles were found, such as the principles of contradiction, of sufficient reason, of the excluded middle, the dictum de omni et nullo, and then the special rules of syllogistic reasoning, as for example Ex meris particularibus aut negativis nihil sequitur; a rationato ad rationem non valet conse-quentia; ²⁹ and so on. That all this came about only slowly and very laboriously, and, until Aristotle, remained very incomplete, is seen in part from the awkward and tedious way in which logical truths are brought out in many of Plato’s dialogues, and even better from what Sextus Empiricus tells us of the controversies of the Megarics concerning the easiest and simplest logical laws, and the laborious way in which they made such laws plain and intelligible (Sextus Empiricus, Adversus Mathematicos, 1. 8, p. 112 seqq.). Aristotle collected, arranged, and corrected all that had been previously discovered, and brought it to an incomparably higher state of perfection. If we thus consider how the course of Greek culture had prepared for and led up to Aristotle’s work, we shall be little inclined to give credit to the statement of Persian authors reported to us by Sir William Jones, who was much prejudiced in their favour, namely that Callisthenes found among the Indians a finished system of logic which he sent to his uncle Aristotle (Asiatic Researches, Vol. IV, p. 163). It is easy to understand that in the dreary Middle Ages the Aristotelian logic was bound to be extremely welcome to the argumentative spirit of the scholastics, which, in the absence of real knowledge, feasted only on formulas and words. It is easy to see that this logic, even in its mutilated Arabic form, would be eagerly adopted, and soon elevated to the centre of all knowledge. Although it has since sunk from its position of authority, it has nevertheless retained up to our own time the credit of a self-contained, practical, and extremely necessary science. Even in our day the Kantian philosophy, which really took its foundation-stone from logic, has awakened a fresh interest in it. In this respect, that is to say, as a means to knowing the essential nature of reason, it certainly merits such interest.

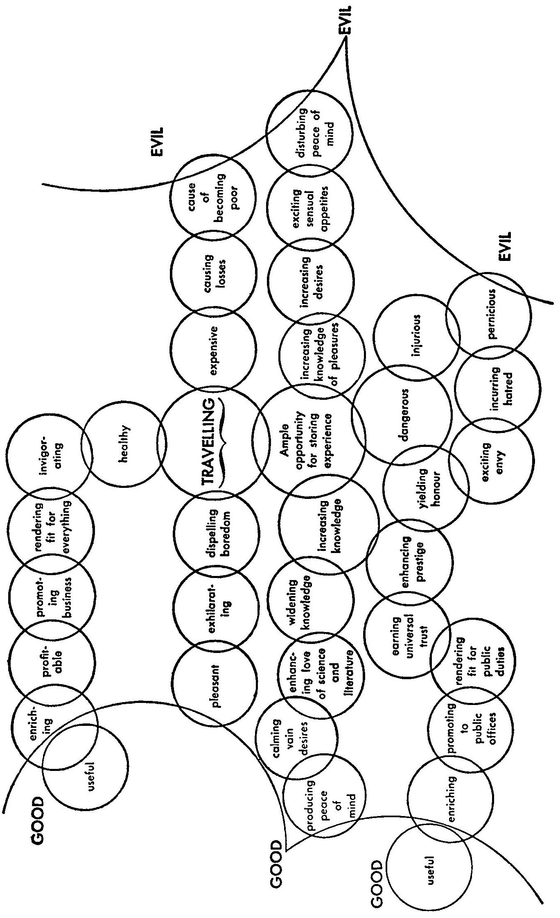
Correct and exact conclusions are reached by our accurately observing the relation of the concept-spheres, and admitting that one sphere is wholly contained in a third only when a sphere is completely contained in another, which other is in turn wholly contained in the third. On the other hand, the art of persuasion depends on our subjecting the relations of the concept-spheres to a superficial consideration only, and then determining these only from one point of view, and in accordance with our intentions, mainly in the following way. If the sphere of a concept under consideration lies only partly in another sphere, and partly also in quite a different sphere, we declare it to be entirely in the first sphere or entirely in the second, according to our intentions. For example, when passion is spoken of, we can subsume this under the concept of the greatest force, of the mightiest agency in the world, or under the concept of irrationality, and this under the concept of powerlessness or weakness. We can continue this method, and apply it afresh with each concept to which the argument leads us. The sphere of a concept is almost invariably shared by several others, each of which contains a part of the province of the first sphere, while itself including something more besides. Of these latter concept-spheres we allow only that sphere to be elucidated under which we wish to subsume the first concept, leaving the rest unobserved, or keeping them concealed. On this trick all the arts of persuasion, all the more subtle sophisms, really depend; for the logical sophisms, such as mentiens, velatus, cornutus,³⁰ and so on, are obviously too clumsy for actual application. I am not aware that anyone hitherto has traced the nature of all sophistication and persuasion back to this ultimate ground of their possibility, and demonstrated this in the peculiar property of concepts, that is to say, the cognitive method of reason. As my discussion has led me to this, I will elucidate the matter, easy though it is to understand, by means of a schema in the accompanying diagram. This shows how the concept-spheres in many ways overlap one another, and thus enable us freely to pass arbitrarily from each concept to others in one direction or another. I do not want anyone to be led by this diagram into attaching more importance to this short incidental discussion than it has in its own right. I have chosen as an illustrative example the concept of travelling. Its sphere overlaps into the province of four others, to each of which the persuasive talker can pass at will. These again overlap into other spheres, several of them into two or more simultaneously; and through these the persuasive talker takes whichever way he likes, always as if it were the only way, and then ultimately arrives at good or evil, according to what his intention was. In going from one sphere to another, it is only necessary always to maintain direction from the centre (the given chief concept) to the circumference, and not go backwards. The manner of clothing such a sophistication in words can be continuous speech or even the strict syllogistic form, as the hearer’s weak side may suggest. The nature of most scientific arguments, particularly of philosophical demonstrations, is not at bottom very different from this. Otherwise how would it be possible for so much at different periods to be not only erroneously assumed (for error itself has a different source), but demonstrated and proved, and then later found to be fundamentally false, such as, for example, the philosophy of Leibniz and Wolff, Ptolemaic astronomy, Stahl’s chemistry, Newton’s theory of colours, and so on? ³¹