§ 15.

Now if with our conviction that perception is the first source of all evidence, that immediate or mediate reference to this alone is absolute truth, and further that the shortest way to this is always the surest, as every mediation through concepts exposes us to many deceptions; if, I say, we now turn with this conviction to mathematics, as it was laid down in the form of a science by Euclid, and has on the whole remained down to the present day, we cannot help finding the path followed by it strange and even perverted. We demand the reduction of every logical proof to one of perception. Mathematics, on the contrary, is at great pains deliberately to reject the evidence of perception peculiar to it and everywhere at hand, in order to substitute for it logical evidence. We must look upon this as being like a man who cuts off his legs in order to walk on crutches, or the prince in Triumph der Empfindsamkeit who flees from the beautiful reality of nature to enjoy a theatrical scene that imitates it. I must now call to mind what I said in the sixth chapter of the essay On the Principle of Sufficient Reason, which I assume to be quite fresh and present in the reader’s memory. Here then I link my observations on to this without discussing afresh the difference between the mere ground of knowledge of a mathematical truth which can be given logically, and the ground of being, which is the immediate connexion of the parts of space and time, to be known only from perception. It is only insight into the ground of being which gives true satisfaction and thorough knowledge. The mere ground of knowledge, on the other hand, always remains on the surface, and can give us a rational knowledge that a thing is as it is, but no rational knowledge why it is so. Euclid chose this latter way to the obvious detriment of the science. For example, at the very beginning, he ought to show once for all how in the triangle angles and sides reciprocally determine one another, and are the reason or ground and consequent of each other, in accordance with the form which the principle of sufficient reason has in mere space, and which there, as everywhere, provides the necessity that a thing is as it is, because another thing, quite different from it, is as it is. Instead of thus giving us a thorough insight into the nature of the triangle, he posits a few disconnected, arbitrarily chosen propositions about the triangle, and gives a logical ground of knowledge of them through a laborious logical proof furnished in accordance with the principle of contradiction. Instead of an exhaustive knowledge of these space-relations, we therefore obtain only a few arbitrarily communicated results from them, and are in the same position as the man to whom the different effects of an ingenious machine are shown, while its inner connexion and mechanism are withheld from him. We are forced by the principle of contradiction to admit that everything demonstrated by Euclid is so, but we do not get to know why it is so. We therefore have almost the uncomfortable feeling that we get after a conjuring trick, and in fact most of Euclid’s proofs are remarkably like such a trick. The truth almost always comes in by the back door, since it follows per accidens from some minor circumstance. Frequently, an apagogic proof shuts all doors one after the other, and leaves open only one, through which merely for that reason we must now pass. Often, as in the theorem of Pythagoras, lines are drawn without our knowing why. It afterwards appears that they were traps, which shut unexpectedly and take prisoner the assent of the learner, who in astonishment has then to admit what remains wholly unintelligible to him in its inner connexion. This happens to such an extent that he can study the whole of Euclid throughout without gaining real insight into the laws of spatial relations, but instead of these, he learns by heart only a few of their results. This really empirical and unscientific knowledge is like that of the doctor who knows disease and remedy, but not the connexion between the two. But all this is what results when we capriciously reject the method of proof and evidence peculiar to one species of knowledge, and forcibly introduce instead of it a method that is foreign to its nature. In other respects, however, the way in which this is carried out by Euclid deserves all the admiration that for so many centuries has been bestowed on him. The method has been followed so far, that his treatment of mathematics has been declared to be the pattern for all scientific presentation. Men tried even to model all the other sciences on it, but later gave this up without really knowing why. In our view, however, this method of Euclid in mathematics can appear only as a very brilliant piece of perversity. When a great error concerning life or science is pursued intentionally and methodically, and is accompanied by universal assent, it is always possible to demonstrate the reason for this in the philosophy that prevails at the time. The Eleatics first discovered the difference, indeed more often the antagonism, between the perceived, ϕαινóμενoν, and the conceived, νooύμενoν,38 and used it in many ways for their philosophemes, and also for sophisms. They were followed later by the Megarics, Dialecticians, Sophists, New Academicians, and Sceptics; these drew attention to the illusion, that is, the deception of the senses, or rather of the understanding which converts the data of the senses into perception, and often causes us to see things to which the faculty of reason positively denies reality, for example, the stick broken in the water, and so on. It was recognized that perception through the senses was not to be trusted unconditionally, and it was hastily concluded that only rational logical thinking established truth, although Plato (in the Parmenides), the Megarics, Pyrrho, and the New Academicians showed by examples (in the way later adopted by Sextus Empiricus) how syllogisms and concepts were also misleading, how in fact they produced paralogisms and sophisms that arise much more easily, and are far harder to unravel, than the illusion in perception through the senses. But this rationalism, which arose in opposition to empiricism, kept the upper hand, and Euclid modelled mathematics in accordance with it. He was therefore necessarily compelled to found the axioms alone on the evidence of perception (ϕαινóμενoν), and all the rest on syllogisms (νooúμενoν). His method remained the prevailing one throughout all the centuries, and was bound so to remain, so long as there was no distinction between pure intuition or perception a priori and empirical perception. Indeed, Euclid’s commentator Proclus appears to have fully recognized this distinction, as he shows in the passage translated by Kepler into Latin in his book De Harmonia Mundi. But Proclus did not attach enough weight to the matter; he raised it in too detached a manner, remained unnoticed, and achieved nothing. Therefore only after two thousand years will Kant’s teaching, destined to bring about such great changes in all the knowledge, thought, and action of European nations, cause such a change in mathematics also. For only after we have learnt from this great mind that the intuitions or perceptions of space and time are quite different from empirical perception, entirely independent of any impression on the senses, conditioning this and not conditioned by it, i.e., are a priori, and hence not in any way exposed to sense-deception—only then can we see that Euclid’s logical method of treating mathematics is a useless precaution, a crutch for sound legs. We see that such a method is like a wanderer who, mistaking at night a bright firm road for water, refrains from walking on it, and goes over the rough ground beside it, content to keep from point to point along the edge of the supposed water. Only now can we affirm with certainty that that which presents itself to us as necessary in the perception of a figure does not come from the figure on the paper, perhaps very imperfectly drawn, or from the abstract concept that we think with it, but immediately from the form of all knowledge, of which we are conscious a priori. This is everywhere the principle of sufficient reason; here, as form of perception, i.e., space, it is the principle of the ground of being; but the evidence and validity of this are just as great and immediate as that of the principle of the ground of knowledge, i.e., logical certainty. Thus we need not and should not leave the peculiar province of mathematics in order to trust merely logical certainty, and prove mathematics true in a province quite foreign to it, namely in the province of concepts. If we stick to the ground peculiar to mathematics, we gain the great advantage that in it the rational knowledge that something is so is one with the rational knowledge why it is so. The method of Euclid, on the other hand, entirely separates the two, and lets us know merely the first, not the second. Aristotle says admirably in the Posterior Analytics (I, 27): ’Axpιβεστέpα δ’έπιστŕ,μɳ έπιστŕ,μɳς xαì πpoτέpα, τoũ ἤτε τoῦ őτι xαì τoῦ διóτι ή αύτή, άλλẋ μή χωpìς őτι, τής τoῦ διóτι. (Subtilior autem et praestantior ea est scientia, quâ QUOD aliquid sit, et CUR sit una simulque intelligimus, non separatim QUOD, et CUR sit.)³⁹ In physics we are satisfied only when the knowledge that something is thus is combined with the knowledge why it is thus. It is no use for us to know that the mercury in the Torricellian tube stands at a height of thirty inches, if we do not also know that it is kept at this height by the counterbalancing weight of the atmosphere. But are we in mathematics to be satisfied with the qualitas occulta of the circle that the segments of any two intersecting chords always form equal rectangles? That this is so is of course proved by Euclid in the 35th proposition of the third book, but why it is so remains uncertain. In the same way, the theorem of Pythagoras teaches us a qualitas occulta of the right-angled triangle; the stilted, and indeed subtle, proof of Euclid forsakes us at the why, and the accompanying simple figure, already known to us, gives at a glance far more insight into the matter, and firm inner conviction of that necessity, and of the dependence of that property on the right angle, than is given by his proof.

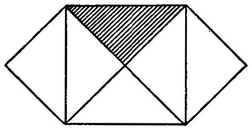
Even in the case when unequal sides contain the right angle, as generally with every possible geometrical truth, it must be possible to reach such a conviction based on perception, because its discovery always started from such a perceived necessity, and only afterwards was the proof thought out in addition. Thus we need only an analysis of the process of thought in the first discovery of a geometrical truth, in order to know its necessity intuitively or perceptively. It is generally the analytic method that I desire for the expounding of mathematics, instead of the synthetic method Euclid made use of. But of course with complicated mathematical truths this will entail very great, though not insuperable, difficulties. Here and there in Germany men are beginning to alter the exposition of mathematics, and to follow more this analytic path. The most positive work in this direction has been done by Herr Kosack, instructor in mathematics and physics at the Nordhausen Gymnasium, who added to the programme for the school examination of 6 April 1852 a detailed attempt to deal with geometry in accordance with my main principles.

To improve the method of mathematics, it is specially necessary to give up the prejudice that demonstrated truth has any advantage over truth known through perception or intuition, or that logical truth, resting on the principle of contradiction, has any advantage over metaphysical truth, which is immediately evident, and to which also belongs the pure intuition of space.

What is most certain yet everywhere inexplicable is the content of the principle of sufficient reason, for this principle in its different aspects expresses the universal form of all our representations and knowledge. All explanation is a tracing back to this principle, a demonstration in the particular case of the connexion of representations expressed generally through it. It is therefore the principle of all explanation, and hence is not itself capable of explanation; nor is it in need of one, for every explanation presupposes it, and only through it obtains any meaning. None of its forms is superior to another; it is equally certain and incapable of demonstration as principle of ground of being, or of becoming, or of acting, or of knowing. The relation of reason or ground to consequent is a necessary one in any one of its forms; indeed, it is in general the origin of the concept of necessity, as its one and only meaning. There is no other necessity than that of the consequent when the reason or ground is given; and there is no reason or ground that does not entail necessity of the consequent. Just as surely, then, as the consequent expressed in the conclusion flows from the ground of knowledge given in the premisses, so does the ground of being in space condition its consequent in space. If I have recognized through perception the relation of these two, then this certainty is just as great as any logical certainty. But every geometrical proposition is just as good an expression of such a relation as is one of the twelve axioms. It is a metaphysical truth, and, as such, is just as immediately certain as is the principle of contradiction itself, which is a metalogical truth, and is the general foundation of all logical demonstration. Whoever denies the necessity, intuitively presented, of the space-relations expressed in any proposition, can with equal right deny the axioms, the following of the conclusion from the premisses, or even the principle of contradiction itself, for all these relations are equally indemonstrable, immediately evident, and knowable a priori. Therefore, if anyone wishes to derive the necessity of space-relations, knowable in intuition or perception, from the principle of contradiction through a logical demonstration, it is just the same as if a stranger wished to enfeoff an estate to the immediate owner thereof. But this is what Euclid has done. Only his axioms is he compelled to leave resting on immediate evidence; all the following geometrical truths are logically proved, namely, under the presupposition of those axioms, from the agreement with the assumptions made in the proposition, or with an earlier proposition, or even from the contradiction between the opposite of the proposition and the assumptions, or the axioms, or the earlier propositions, or even itself. But the axioms themselves have no more immediate evidence than any other geometrical proposition has, but only greater simplicity by their smaller content.

When an accused person is examined, his statements are taken down in evidence, in order to judge of their truth from their agreement and consistency. But this is a mere makeshift, and we ought not to put up with it if we can investigate the truth of each of his statements directly and by itself, especially as he might consistently lie from the beginning. But it is by this first method that Euclid investigated space. He did indeed start from the correct assumption that nature must be consistent everywhere, and therefore also in space, its fundamental form. Therefore, since the parts of space stand to one another in the relation of reason or ground to consequent, no single determination of space can be other than it is without being in contradiction with all the others. But this is a very troublesome, unsatisfactory, and roundabout way, which prefers indirect knowledge to direct knowledge that is just as certain; which further separates the knowledge that something is from the knowledge why it is, to the great disadvantage of science; and which finally withholds entirely from the beginner insight into the laws of space, and indeed renders him unaccustomed to the proper investigation of the ground and inner connexion of things. Instead of this, it directs him to be satisfied with a mere historical knowledge that a thing is as it is. But the exercise of acuteness, mentioned so incessantly in praise of this method, consists merely in the fact that the pupil practises drawing conclusions, i.e., applying the principle of contradiction, but specially that he exerts his memory in order to retain all those data whose agreement and consistency are to be compared.

Moreover, it is worth noting that this method of proof was applied only to geometry and not to arithmetic. In arithmetic, on the contrary, truth is really allowed to become clear through perception alone, which there consists in mere counting. As the perception of numbers is in time alone, and therefore cannot be represented by a sensuous schema like the geometrical figure, the suspicion that perception was only empirical, and hence subject to illusion, disappeared in arithmetic. It was only this suspicion that was able to introduce the logical method of proof into geometry. Since time has only one dimension, counting is the only arithmetical operation, to which all others can be reduced. Yet this counting is nothing but intuition or perception a priori, to which we do not hesitate to refer, and by which alone everything else, every calculation, every equation, is ultimately verified. For example, we do not prove that 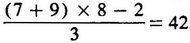, but refer to pure intuition in time, to counting; thus we make each individual proposition an axiom. Instead of the proofs that fill geometry, the whole content of arithmetic and algebra is thus a mere method for the abbreviation of counting. As mentioned above, our immediate perception of numbers in time does not extend to more than about ten. Beyond this an abstract concept of number, fixed by a word, must take the place of perception; thus perception is no longer actually carried out, but is only quite definitely indicated. Yet even so, through the important expedient of the order of ciphers, enabling larger numbers always to be represented by the same small ones, an intuitive or perceptive evidence of every sum or calculation is made possible, even where so much use is made of abstraction that not only the numbers, but indefinite quantities and whole operations are thought only in the abstract, and are indicated in this respect, such as 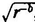, so that they are no longer performed, but only symbolized.

With the same right and certainty we could enable truth to be established in geometry, just as in arithmetic, solely through pure intuition a priori. In fact, it is always this necessity, known from perception according to the principle of the ground or reason of being, which gives geometry its great evidence, and on which the certainty of its propositions rests in the consciousness of everyone. It is certainly not the stilted logical proof, which is always foreign to the matter, is generally soon forgotten without detriment to conviction, and could be dispensed with entirely, without diminishing the evidence of geometry. For geometry is quite independent of such proof, which always proves only what we are already through another kind of knowledge fully convinced of. To this extent it is like a cowardly soldier who gives another wound to an enemy killed by someone else, and then boasts that he himself killed him.⁴⁰

As a result of all this, it is hoped there will be no doubt that the evidence of mathematics, which has become the pattern and symbol of all evidence, rests essentially not on proofs, but on immediate intuition or perception. Here, as everywhere, that is the ultimate ground and source of all truth. Yet the perception forming the basis of mathematics has a great advantage over every other perception, and hence over the empirical. Thus as it is a priori, and consequently independent of experience which is always given only partially and successively, everything is equally near to it, and we can start either from the reason or ground or from the consequent, as we please. Now this endows it with a complete certainty and infallibility, for in it the consequent is known from the ground or reason, and this knowledge alone has necessity. For example, the equality of the sides is known as established through the equality of the angles. On the other hand, all empirical perception and the greater part of all experience proceed only conversely from the consequent to the ground. This kind of knowledge is not infallible, for necessity belongs alone to the consequent in so far as the ground is given, and not to knowledge of the ground from the consequent, for the same consequent can spring from different grounds. This latter kind of knowledge is always only induction, i.e., from many consequents pointing to one ground, the ground is assumed as certain; but as all the cases can never be together, the truth here is never unconditionally certain. Yet all knowledge through sensuous perception and the great bulk of experience have only this kind of truth. The affection of a sense induces the understanding to infer the cause from the effect, but since the conclusion from what is established (the consequent) to the ground is never certain, illusion, which is deception of the senses, is possible, and often actual, as was said previously. Only when several or all of the five senses receive affections pointing to the same cause does the possibility of illusion become small. Even then it still exists, for in certain cases, such as with counterfeit coins, the whole sensitive faculty is deceived. All empirical knowledge, and consequently the whole of natural science, is in the same position, leaving aside its pure (or as Kant calls it metaphysical) part. Here also the causes are known from the effects; therefore all natural philosophy rests on hypotheses which are often false, and then gradually give way to others that are more correct. Only in the case of intentionally arranged experiments does knowledge proceed from the cause to the effect, in other words, does it go the sure and certain way; but these experiments are themselves undertaken only in consequence of hypotheses. For this reason, no branch of natural science, such as physics, or astronomy, or physiology, could be discovered all at once, as was possible with mathematics or logic, but it required and requires the collected and compared experiences of many centuries. Only empirical confirmation of many kinds brings the induction on which the hypothesis rests so near to completeness that in practice it takes the place of certainty. It is regarded as being no more detrimental to the hypothesis, its source, than is the incommensurability of straight and curved lines to the application of geometry, or perfect exactness of the logarithm, which is incapable of attainment, to arithmetic. For just as the squaring of the circle, and the logarithm, are brought infinitely near to correctness through infinite fractions, so also through manifold experience induction, i.e., knowledge of the ground from the consequents, is brought to mathematical evidence, i.e., to knowledge of the consequent from the ground, not indeed infinitely, but yet so close that the possibility of deception becomes so small that we can neglect it. But yet the possibility is there; for example, the conclusion from innumerable cases to all cases, i.e., in reality to the unknown ground on which all depend, is a conclusion of induction. Now what conclusion of this kind seems more certain than the one that all human beings have their heart on the left side? Yet there are extremely rare and quite isolated exceptions of persons whose heart is on the right side. Sense-perception and the science of experience have therefore the same kind of evidence. The advantage that mathematics, pure natural science, and logic as knowledge a priori have over them rests merely on the fact that the formal element of knowledge, on which all that is a priori is based, is given as a whole and at once. Here, therefore, we can always proceed from the ground to the consequent, but in the other kind of knowledge often only from the consequent to the ground. In other respects, the law of causality, or the principle of sufficient reason of becoming, which guides empirical knowledge, is in itself just as certain as are those other forms of the principle of sufficient reason followed by the above-mentioned sciences a priori. Logical proofs from concepts or syllogisms have the advantage of proceeding from the ground to the consequent, just as has knowledge through a priori perception; thus in themselves, that is to say, according to their form, they are infallible. This has been largely instrumental in bringing proofs generally into such great repute. But this infallibility of theirs is relative; they subsume merely under the main principles of science. It is these, however, that contain the whole material truth of science, and they cannot again be merely demonstrated, but must be founded on perception. In the few mentioned a priori sciences this perception is pure, but otherwise it is always empirical, and is raised to the universal only through induction. If, therefore, in the sciences of experience the particular is proved from the general, the general nevertheless has again obtained its truth only from the particular; it is only a granary of accumulated stocks, not a soil that is itself productive.

So much for the establishment of truth. Of the source and possibility of error, many explanations have been attempted since Plato’s metaphorical solutions of the dovecot, where the wrong pigeon is caught, and so on (Theaetetus [197 ff.], p. 167 et seqq.). Kant’s vague, indefinite explanation of the origin of error by means of the diagram of diagonal motion is found in the Critique of Pure Reason (p. 294 of the first edition, and p. 350 of the fifth). As truth is the relation of a judgement to its ground of knowledge, it is certainly a problem how the person judging can really believe he has such a ground and yet not have it, that is to say how error, the deception of the faculty of reason, is possible. I find this possibility wholly analogous to that of illusion, or deception of the understanding, previously explained. My opinion is (and this gives that explanation its place here) that every error is a conclusion from the consequent to the ground, which indeed is valid when we know that the consequent can have that ground and absolutely no other; otherwise it is not. The person making the error either assigns to the consequent a ground it cannot possibly have, wherein he shows actual want of understanding, i.e., deficiency in the ability to know immediately the connexion between cause and effect. Or, as is more often the case, he attributes to the consequent a ground that is indeed possible, yet he adds to the major proposition of his conclusion from the consequent to the ground that the aforesaid consequent arises always only from the ground mentioned by him. He could be justified in doing this only by a complete induction, which, however, he assumes without having made it. This “always” is therefore too wide a concept, and should be replaced by sometimes or generally. The conclusion would thus turn out to be problematical, and as such would not be erroneous. That the man who errs should proceed in the way mentioned is due either to haste or too limited a knowledge of what is possible, for which reason he does not know the necessity of the induction to be made. Error therefore is wholly analogous to illusion. Both are conclusions from the consequent to the ground; the illusion, brought about always according to the law of causality, by the mere understanding, and thus immediately, in perception itself; the error, brought about according to all the forms of the principle of sufficient reason, by our rational faculty, and thus in thought proper, yet most frequently according to the law of causality, as is proved by the three following examples, which may be regarded as types or representatives of the three kinds of error. (1) The illusion of the senses (deception of the understanding) gives rise to error (deception of reason); for example, if we mistake a painting for a high relief, and actually take it to be such; it happens through a conclusion from the following major premiss: “If dark grey here and there passes through all shades into white, the cause is always the light striking unequally projections and depressions, ergo—.” (2) “If money is missing from my safe, the cause is always that my servant has a skeleton key, ergo—.” (3) “If the solar image, broken through the prism, i.e., moved up or down, now appears elongated and coloured instead of round and white as previously, then the cause is always that in light there are differently coloured, and at the same time differently refrangible, homogeneous light-rays that, moved apart by their different refrangibility, now give an elongated, and at the same time variously coloured, image, ergo—bibamus!” It must be possible to trace every error to such a conclusion, drawn from a major premiss that is often only falsely generalized, hypothetical, and the result of assuming a ground to the consequent. Only some mistakes in calculation are to be excepted, which are not really errors, but mere mistakes. The operation stated by the concepts of the numbers has not been carried out in pure intuition or perception, in counting, but another operation instead.

As regards the content of the sciences generally, this is really always the relation of the phenomena of the world to one another according to the principle of sufficient reason, and on the guiding line of the Why, which has validity and meaning only through this principle. Explanation is the establishment of this relation. Therefore, explanation can never do more than show two representations standing to each other in the relation of that form of the principle of sufficient reason ruling in the class to which they belong. If it has achieved this, we cannot be further asked the question why, for the relation demonstrated is that which simply cannot be represented differently, in other words, it is the form of all knowledge. Therefore we do not ask why 2 + 2 = 4, or why the equality of the angles in a triangle determines the equality of the sides, or why any given cause is followed by its effect, or why the truth of a conclusion is evident from the truth of the premisses. Every explanation not⁴¹ leading back to such a relation of which no Why can further be demanded, stops at an accepted qualitas occulta; but this is also the character of every original force of nature. Every explanation of natural science must ultimately stop at such a qualitas occulta, and thus at something wholly obscure. It must therefore leave the inner nature of a stone just as unexplained as that of a human being; it can give as little account of the weight, cohesion, chemical properties, etc. of the former, as of the knowing and acting of the latter. Thus, for example, weight is a qualitas occulta, for it can be thought away, and hence it does not follow from the form of knowledge as something necessary. Again, this is the case with the law of inertia, which follows from the law of causality; hence a reference to this is a perfectly adequate explanation. Two things are absolutely inexplicable, in other words, do not lead back to the relation expressed by the principle of sufficient reason. The first of these is the principle of sufficient reason itself in all its four forms, because it is the principle of all explanation, which has meaning only in reference to it; the second is that which is not reached by this principle, but from which arises that original thing in all phenomena; it is the thing-in-itself, knowledge of which is in no wise subject to the principle of sufficient reason. Here for the present we must rest content not to understand this thing-in-itself, for it can be made intelligible only by the following book, where we shall also take up again this consideration of the possible achievements of the sciences. But there is a point where natural science, and indeed every science, leaves things as they are, since not only its explanation of them, but even the principle of this explanation, namely the principle of sufficient reason, does not go beyond this point. This is the real point where philosophy again takes up things and considers them in accordance with its method, which is entirely different from the method of science. In the essay On the Principle of Sufficient Reason, § 51, I have shown how in the different sciences the main guiding line is one form or another of this principle; in fact, the most appropriate classification of the sciences might perhaps be made in accordance therewith. But, as I have said, every explanation given in accordance with this guiding line is merely relative. It explains things in reference to one another, but it always leaves unexplained something that it presupposes. In mathematics, for example, this is space and time; in mechanics, physics, and chemistry, it is matter, qualities, original forces, laws of nature; in botany and zoology, it is the difference of species and life itself; in history, it is the human race with all its characteristics of thought and will. In all these it is the principle of sufficient reason in the form appropriate for application in each case. Philosophy has the peculiarity of presupposing absolutely nothing as known; everything to it is equally strange and a problem; not only the relations of phenomena, but also those phenomena themselves, and indeed the principle of sufficient reason itself, to which the other sciences are content to refer everything. In philosophy, however, nothing would be gained by such a reference, for one link of the series is just as foreign and strange to it as another. Moreover, that kind of connexion is itself just as much a problem for philosophy as what is joined together by that connexion, and this again is as much a problem after the combination thus explained as before it. For, as we have said, just what the sciences presuppose and lay down as the basis and limit of their explanation is precisely the real problem of philosophy, which consequently begins where the sciences leave off. Proofs cannot be its foundation, for these deduce unknown principles from others that are known; but to it everything is equally unknown and strange. There can be no principle in consequence of which the world with all its phenomena would first of all exist; therefore it is not possible, as Spinoza wished, to deduce a philosophy that demonstrates ex firmis principiis. Philosophy is also the most universal rational knowledge (Wissen), whose main principles, therefore, cannot be deductions from another principle still more universal. The principle of contradiction establishes merely the agreement of concepts, and does not itself give concepts. The principle of sufficient reason explains connexions and combinations of phenomena, not the phenomena themselves. Therefore, philosophy cannot start from these to look for a causa efficiens or a causa finalis of the whole world. The present philosophy, at any rate, by no means attempts to say whence or for what purpose the world exists, but merely what the world is. But here the Why is subordinated to the What, for it already belongs to the world, as it springs merely from the form of its phenomenon, the principle of sufficient reason, and only to this extent has it meaning and validity. Indeed, it might be said that everyone knows without further help what the world is, for he himself is the subject of knowing of which the world is representation, and so far this would be true. But this knowledge is a knowledge of perception, is in the concrete. The task of philosophy is to reproduce this in the abstract, to raise to a permanent rational knowledge successive, variable perceptions, and generally all that the wide concept of feeling embraces and describes merely negatively as not abstract, distinct, rational knowledge. Accordingly, it must be a statement in the abstract of the nature of the whole world, of the whole as well as of all the parts. However, in order not to be lost in an endless multitude of particular judgements, it must make use of abstraction, and think everything individual in the universal, and its differences also in the universal. It will therefore partly separate, partly unite, in order to present to rational knowledge the whole manifold of the world in general, according to its nature, condensed and summarized into a few abstract concepts. Yet through these concepts, in which it fixes the nature of the world, the whole individual as well as the universal must be known, and hence the knowledge of both must be closely bound up. Therefore, aptitude for philosophy consists precisely in what Plato put it in, namely in knowing the one in the many and the many in the one. Accordingly, philosophy will be a sum of very universal judgements, whose ground of knowledge is immediately the world itself in its entirety, without excluding anything, and hence everything to be found in human consciousness. It will be a complete recapitulation, so to speak, a reflection of the world in abstract concepts, and this is possible only by uniting the essentially identical into one concept, and by relegating the different and dissimilar to another. Bacon already set philosophy this task, when he said: ea demum vera est philosophia, quae mundi ipsius voces fidelissime reddit, et veluti dictante mundo conscripta est, et nihil aliud est, quam ejusdem SIMULACRUM ET REFLECTIO, neque addit quidquam de proprio, sed tantum iterat et resonat (De Augmentis Scientiarum, 1. 2, c. 13).⁴² However, we take this in a more extended sense than Bacon could conceive at that time.

The agreement which all aspects and parts of the world have with one another, just because they belong to one whole, must also be found again in this abstract copy of the world. Accordingly, in this sum-total of judgements one could to a certain extent be derived from another, and indeed always reciprocally. Yet in addition to this they must first exist, and therefore be previously laid down as immediately established through knowledge of the world in the concrete, the more so as all direct proofs are more certain than those that are indirect. Their harmony with one another, by virtue of which they flow together even into the unity of one thought, and which springs from the harmony and unity of the world of perception itself, their common ground of knowledge, will therefore not be used as the first thing for establishing them, but will be added only as confirmation of their truth. This problem itself can become perfectly clear only by its solution.⁴³