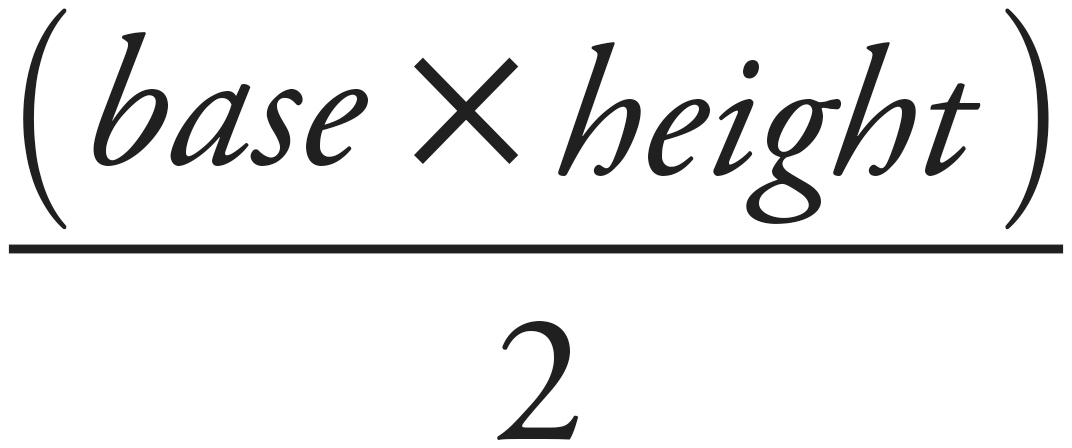Chapter 12

Plane Geometry

The ACT test writers tell us there will be approximately 23 geometry questions on the Math test, 14 of which supposedly cover plane geometry. It’s better, however, to think of the topic breakdown in broader terms rather than these specific numbers. For one thing, many problems incorporate several concepts: You even need algebra to solve many geometry questions, so would the ACT test writers count a question like that in the algebra or plane geometry column?

What matters most is that you can identify the topics that can make a question Now, Later, or Never for you.

While ACT test writers occasionally may throw in a more advanced formula or complex shape, the majority of the questions test the basic rules on the basic shapes. This chapter will review a cross-section of those formulas and concepts and give you a strategic approach to apply those rules on the ACT.

CRACKING THE GEOMETRY ON THE ACT

Plug-and-chug geometry questions can have so much information in them that they feel like word problems. So treat them like word problems. Let’s review the basic approach to word problems. We’ll then add some points specific to geometry.

Step 1: Know the Question

Know the question. Read the whole problem before calculating anything, and underline the actual question.

Step 2: Let the Answers Help

Let the answers help. Look for clues on how to solve and ways to use POE (Process of Elimination).

Step 3: Break the Problem into Bite-Sized Pieces

Break the problem into bite-sized pieces. When you read the problem a second time, calculate at each step necessary and watch out for tricky phrasing.

For geometry questions, Step 3 has two specific additions:

Step 3a: Write all the information given in the problem on the figure. If there is no figure, draw your own.

Step 3b: Write down any formulas you need and fill in any information you have.

Geometry BFFs: POE and Ballparking

Step 2 of the basic approach is particularly important to geometry questions. In the last few chapters, we’ve seen how POE and Ballparking can help to narrow down the answer choices when you’re confused. Before you rush to calculate, Ballparking in particular will help you a ton on geometry problems because most figures are drawn to scale.

To Scale or Not to Scale?

That is the question. The ACT makes a big deal in the instructions about the fact that their figures are “NOT necessarily drawn to scale.” Here’s the thing, though: They usually are drawn to scale or at least enough to use them in broad strokes. Use Ballparking to eliminate answers that are too big or too small rather than to determine a precise value. Questions on angles and area especially lend themselves to Ballparking. The main place to be skeptical is on those problems that ask questions like, “Which of the following must be true?” Those are the ones whose figures can be purposely misleading.

In most other cases, if you know how to use the figures that are given (or how to draw your own), you can eliminate several wrong answers before doing any math at all. Let’s see how this works.

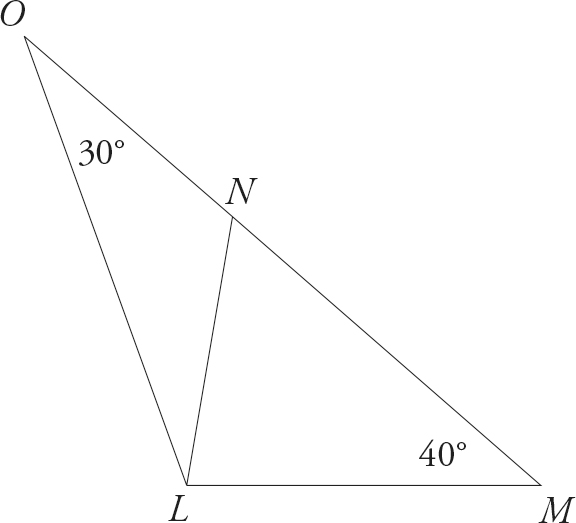
How Big Is Angle NLM?

Obviously, you don’t know exactly how big this angle is, but it would be easy to compare it with an angle whose measure you do know exactly. Let’s compare it with a 90° angle.

Angle NLM is clearly a bit less than 90°. Now look at the following problem, which asks about the same angle NLM.

1. In the figure below, O, N, and M are collinear. If the lengths of ON and NL are the same, the measure of angle LON is 30°, and angle LMN is 40°, what is the measure of angle NLM ?

A.   30°

B.   80°

C.   90°

D. 110°

E. 120°

Here’s How to Crack It

Start with Step 1: Know the question. Underline what is the measure of angle NLM ? and even mark the angle on your figure. You don’t want to answer for the wrong angle. Now move to Step 2, and let’s focus on eliminating answer choices that don’t make sense. We’ve already decided that ∠NLM is a little less than 90°, which means we can eliminate (C), (D), and (E). How much less than 90°? 30° is a third of 90°. Could ∠NLM be that small? No way! The answer to this question must be (B).

In this case, it wasn’t necessary to do any “real” geometry at all to get the question right, but it took about half the time. ACT has to give you credit for right answers no matter how you get them. Revenge is sweet. What’s more, if you worked this problem the “real” way, you might have picked one of the other answers: As you can imagine, every answer choice gives some partial answer that you would’ve seen as you worked the problem.

Let’s Do It Again

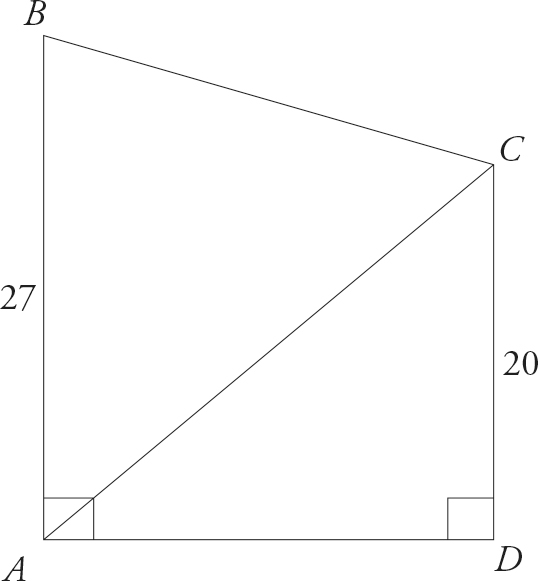
2. In the figure below, if AB = 27, CD = 20, and the area of triangle ADC = 240, what is the area of polygon ABCD?

A.    420

B.    480

C.    540

D.    564

E. 1,128

Here’s How to Crack It

Start with Step 1: Know the question. Underline what is the area of polygon ABCD ? This polygon is not a conventional figure, but if we had to choose one figure that the polygon resembled, we might pick a rectangle. Try drawing a line at a right angle from the line segment AB so that it touches point C, thus creating a rectangle. It should look like the following:

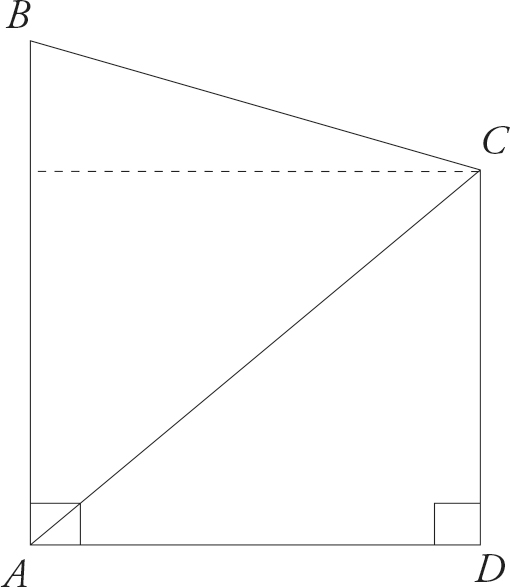
The area of polygon ABCD is equal to the area of the rectangle you’ve just formed, plus a little bit at the top. The problem tells you that the area of triangle ADC is 240. What is the area of the rectangle you just created? If you said 480, you are exactly right, whether you knew the geometric rules that applied or whether you just measured it with your eyes.

So the area of the rectangle is 480. Roughly speaking, then, what should the area of the polygon be? A little more. Let’s look at the answer choices. Choices (F) and (G) are either less than or equal to 480; get rid of them. Choices (H) and (J) both seem possible; they are both a little more than 480; let’s hold on to them. Choice (K) seems pretty crazy. We want more than 480, but 1,128 is ridiculous.

What Should I Do If There Is No Diagram?

Draw one! It’s always easier to understand a problem when you can see it in front of you. If possible, draw your figure to scale so that you can estimate the answer as well.

The answer to this question is (J). To get this final answer, you’ll need to use a variety of area formulas, which we’ll explore later in this chapter. For now, though, notice that your chances of guessing have increased from 20% to 50% with a little bit of quick thinking. Now what should you do? If you know how to do the problem, you do it. If you don’t or if you are running out of time, you guess and move on.

However, even as we move in to the “real” geometry in the remainder of this chapter, don’t forget:

Always look for opportunities to Ballpark on geometry problems even if you know how to do them the “real” way.

GEOMETRY REVIEW

By using the diagrams ACT has so thoughtfully provided, and by making your own diagrams when they are not provided, you can often eliminate several of the answer choices. In some cases, you’ll be able to eliminate every choice but one. Of course, you will also need to know the actual geometry concepts that ACT is testing. We’ve divided our review into the following four topics:

• Angles and lines

• Triangles

• Four-sided figures

• Circles

ANGLES AND LINES

Here is a line.

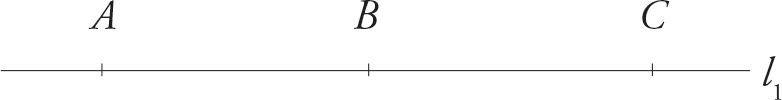
A line extends forever in either direction. This line, called l₁, has three points on it: A, B, and C. These three points are said to be collinear because they are all on the same line. The piece of the line in between points A and B is called a line segment. ACT will refer to it as segment AB or simply AB. A and B are the endpoints of segment AB.

A line forms an angle of 180°. If that line is cut by another line, it divides that 180° into two pieces that together add up to 180°.

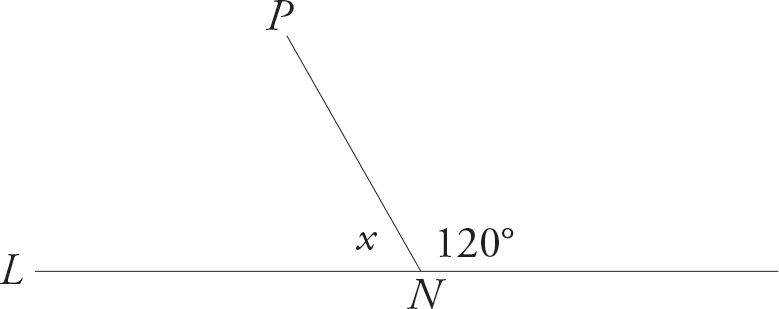
In the above diagram, what is the value of x? If you said 60°, you are correct. To find ∠x, just subtract 120° from 180°.

An angle can also be described by points on the lines that intersect to form the angle and the point of intersection itself, with the middle letter corresponding to the point of intersection. For example, in the previous diagram, ∠x could also be described as ∠LNP. On the ACT, instead of writing out “angle LNP,” they’ll use math shorthand and put ∠LNP instead. So “angle x” becomes ∠x.

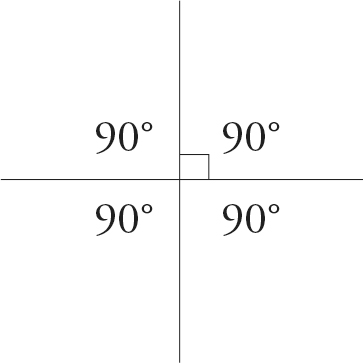
If there are 180° above a line, there are also 180° below the line, for a total of 360°.

When two lines intersect, they form four angles, represented below by letters A, B, C, and D. ∠A and ∠B together form a straight line, so they add up to 180°.

Angles that add up to 180° are called supplementary angles. ∠A and ∠C are opposite from each other and always equal each other, as are ∠B and ∠D. Angles like these are called vertical angles.

In the previous figure, what is the value of ∠x? If you said 80°, you’re right. Together with the 100° angle, x forms a straight line. What is the value of ∠y? If you said 80°, you’re right again. These two angles are vertical and must equal each other. The four angles together add up to 360°.

When two lines meet in such a way that 90° angles are formed, the lines are called perpendicular. The little box at the point of intersection of two lines below indicates that they are perpendicular. It stands to reason that all four of these angles have a value of 90°.

When two lines in the same plane are drawn so that they could extend into infinity without ever meeting, they are called parallel. In the figure below, l₁ is parallel to l₂. The symbol for parallel is | |.

When two parallel lines are cut by a third line, eight angles are formed, but in fact, there are really only two—a big one and a little one. Look at the diagram below.

If ∠A = 110°, then ∠B must equal 70° (together they form a straight line). ∠D is vertical to ∠B, which means that it must also equal 70°. ∠C is vertical to ∠A, so it must equal 110°.

The four angles ∠E, ∠F, ∠G, and ∠H are in exactly the same proportion as the angles above. The little angles are both 70°. The big angles are both 110°.

Try the following problem.

1. In the figure below, line L is parallel to line M. Line N intersects both L and M, with angles a, b, c, d, e, f, g, and h as shown below. Which of the following lists includes all the angles that are supplementary to ∠a?

A. Angles b, d, f, and h

B. Angles c, e, and g

C. Angles b, d, and c

D. Angles e, f, g, and h

E. Angles d, c, h, and g

Here’s How to Crack It

An angle is supplementary to another angle if the two angles together add up to 180°. Because ∠a is one of the eight angles formed by the intersection of a line with two parallel lines, we know that there are really only two angles: a big one and a little one. ∠a is a big one. Thus, only the small angles would be supplementary to it. Which angles are those? The correct answer is (A). By the way, if you think back to the last chapter and apply what you learned there, could you have Plugged In on this problem? Of course you could have. After all, there are variables in the answer choices. Sometimes it is easier to see the correct answer if you substitute real values for the angles instead of just looking at them as a series of variables. Just because a problem involves geometry doesn’t mean that you can’t Plug In.

TRIANGLES

A triangle is a three-sided figure whose inside angles always add up to 180°. The largest angle of a triangle is always opposite its largest side. Thus, in triangle XYZ below, XY would be the largest side, followed by YZ, followed by XZ. On the ACT, “triangle XYZ” will be written as ΔXYZ.

The ACT likes to ask about certain kinds of triangles in particular.

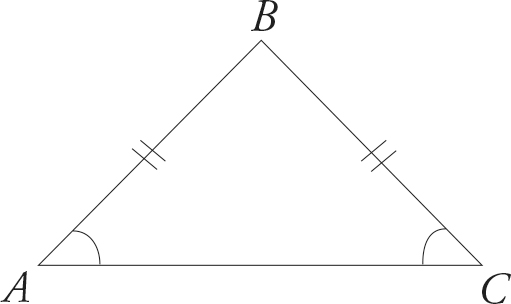
An isosceles triangle has two equal sides. The angles opposite those sides are also equal. In the isosceles triangle above, if ∠A = 50°, then so does ∠C. If AB = 6, then so does BC

An equilateral triangle has three equal sides and three equal angles. Because the three equal angles must add up to 180°, all three angles of an equilateral triangle are always equal to 60°.

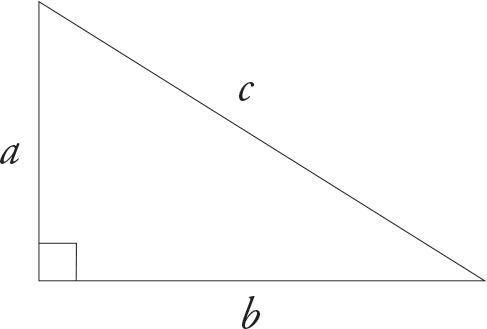
A right triangle has one inside angle that is equal to 90°. The longest side of a right triangle (the one opposite the 90° angle) is called the hypotenuse.

Pythagoras, a Greek mathematician, discovered that the sides of a right triangle are always in a particular proportion, which can be expressed by the formula a² + b² = c², where a and b are the shorter sides of the triangle, and c is the hypotenuse. This formula is called the Pythagorean Theorem.

Pythagoras’s Other Theorem

Pythagoras also developed a theory about the transmigration of souls. So far, this has not been proven, nor will it help you on this exam.

There are certain right triangles that the test writers at ACT find endlessly fascinating. Let’s test out the Pythagorean theorem on the first of these.

3² + 4² = c²

9 + 16 = 25

c² = 25, so c = 5

The ACT writers adore the 3-4-5 triangle and use it frequently, along with its multiples, such as the 6-8-10 triangle and the 9-12-15 triangle. Of course, you can always use the Pythagorean theorem to figure out the third side of a right triangle, as long as you have the other two sides, but because ACT problems almost invariably use “triples” like the ones we’ve just mentioned, it makes sense just to memorize them.

The ACT has three commonly used right-triangle triples.

3-4-5 (and its multiples)

5-12-13 (and its multiples)

7-24-25 (not as common as the other two)

Don’t Get Snared

• Is this a 3-4-5 triangle?

No, because the hypotenuse of a right triangle must be its longest side—the one opposite the 90° angle. In this case, we must use the Pythagorean Theorem to discover side c: 3² + c² = 16, so c = .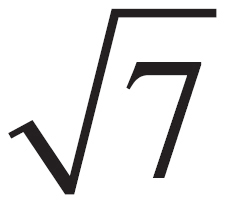

• Is this a 5-12-13 triangle?

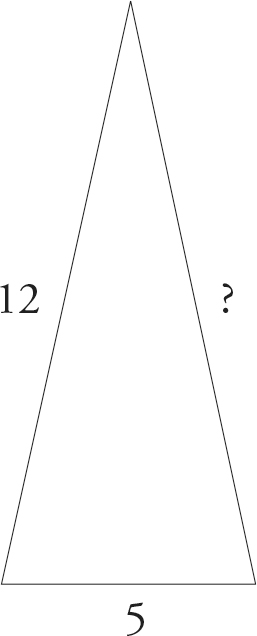
No, because the Pythagorean Theorem—and triples—apply only to right triangles. We can’t determine definitively the third side of this triangle without knowing the specific angle measures.

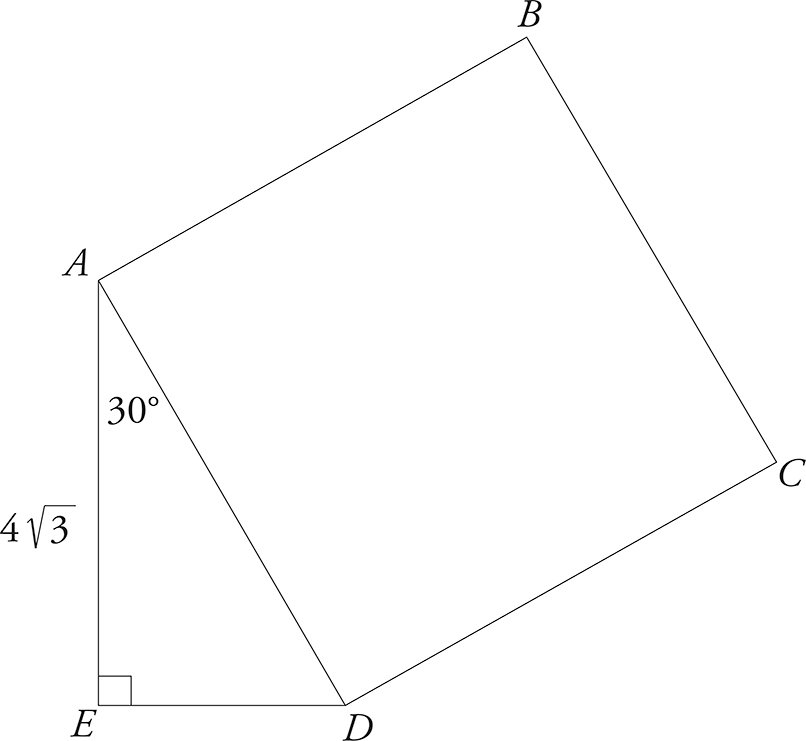
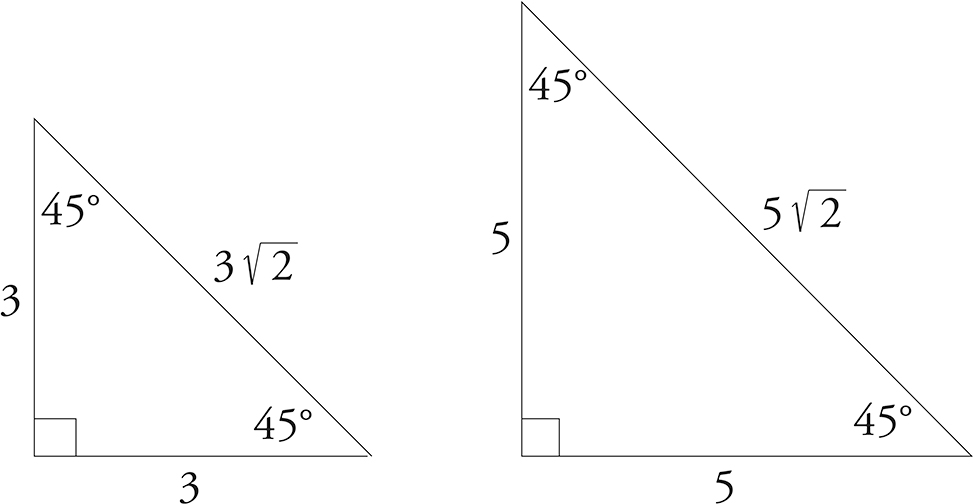
The Isosceles Right Triangle

As fond as the ACT test writers are of triples, they are even fonder of two other right triangles. The first is called the isosceles right triangle. The sides and angles of the isosceles right triangle are always in a particular proportion.

Be on the Lookout…

for problems in which the application of the Pythagorean Theorem is not obvious. For example, every rectangle contains two right triangles. That means that if you know the length and width of the rectangle, you also know the length of the diagonal, which is the hypotenuse of both triangles created by the diagonal.

You could use the Pythagorean Theorem to prove this (or you could just take our word for it). Whatever the value of the two equal sides of the isosceles right triangle, the hypotenuse is always equal to one of those sides times . Here are two examples.

The 30-60-90 Triangle

The other right triangle tested frequently on the ACT is the 30-60-90 triangle, which also always has the same proportions.

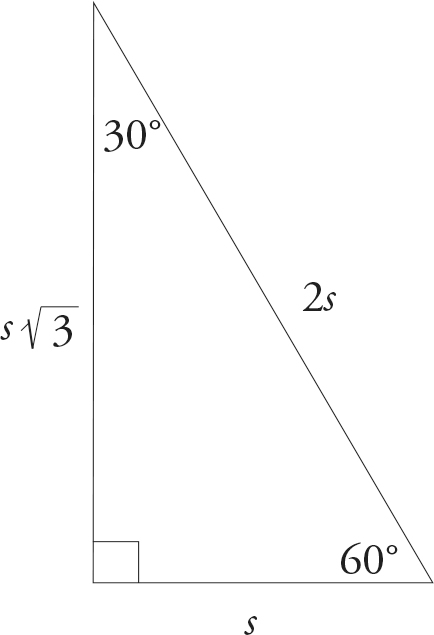
You can use the Pythagorean Theorem to prove this (or you can just take our word for it). Whatever the value of the short side of the 30-60-90 triangle, the hypotenuse is always twice as large. The medium side is always equal to the short side times 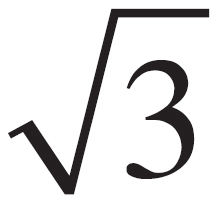. Here are two examples.

Because these triangles are tested so frequently, it makes sense to memorize the proportions, rather than waste time deriving them each time they appear.

Don’t Get Snared

• In the isosceles right triangle below, are the sides equal to 3?

  

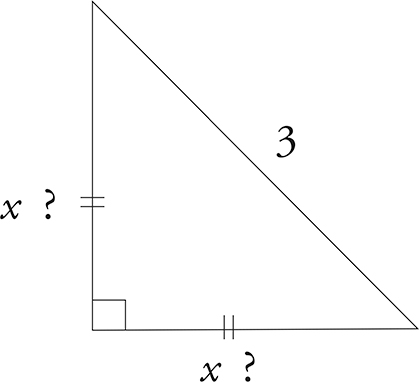
No. Remember, in an isosceles right triangle, hypotenuse = the side . In this case, 3 = the side . If we solve for the side, we get 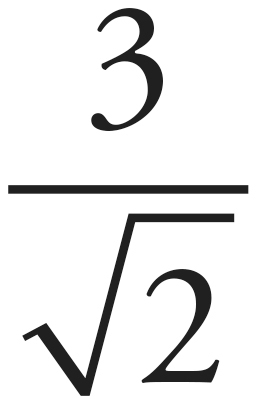the side.

For arcane mathematical reasons, we are not supposed to leave a radical in the denominator, but we can multiply top and bottom by to get .

• In the right triangle below, is x equal to 4?

  

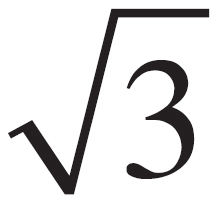No. Even though it is one of ACT’s favorites, you have to be careful not to see a 30-60-90 where none exists. In the triangle above, the short side is half of the medium side, not half of the hypotenuse. This is some sort of right triangle all right, but it is not a 30-60-90. The hypotenuse, in case you’re curious, is really 4.

Area

The area of a triangle can be found using the following formula:

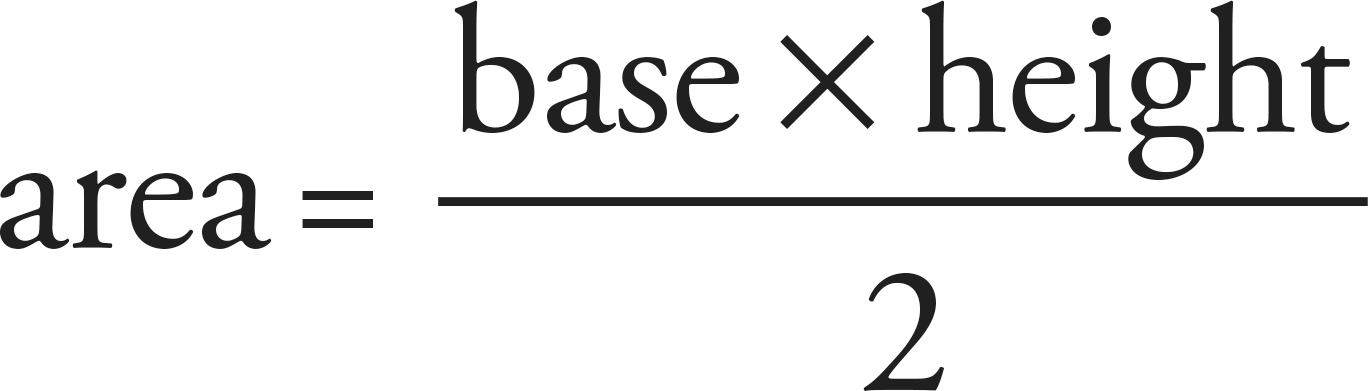
Height is measured as the perpendicular distance from the base of the triangle to its highest point.

In all three of the above triangles, the area is

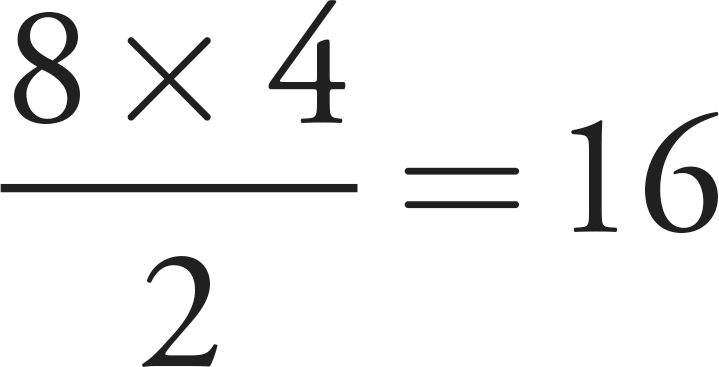
Don’t Get Snared

• Sometimes the height of a triangle can be outside the triangle itself, as we just saw in the second example.

• In a right triangle, the height of the triangle can also be one of the sides of the triangle, as we just saw in the third example. However, be careful when finding the area of a non-right triangle. Simply because you know two sides of the triangle does not mean that you have the height of the triangle.

Similar Triangles

Two triangles are called similar if their angles have the same degree measures. This means their sides will be in proportion. For example, the two triangles below are similar.

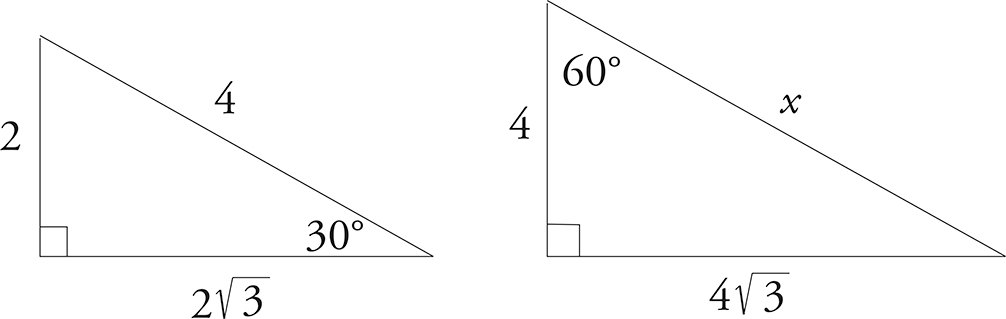
Because the sides of the two triangles are in the same proportion, you can find the missing side, x, by setting up a proportion equation.

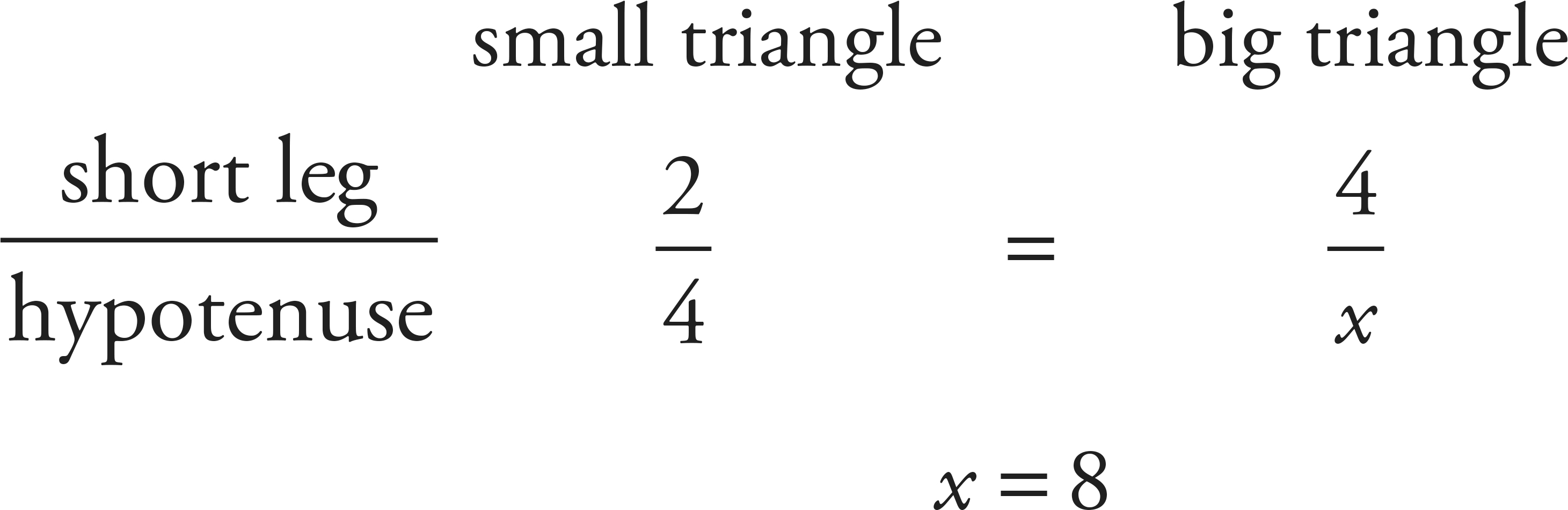
ACT TRIANGLE PROBLEMS

In this chapter, we’ve pretty much given you all the basic triangle information you’ll need to do the triangle problems on the ACT. The trick is that you’ll have to use a lot of this information all at once. Let’s have a look at a typical ACT triangle problem and see how to use the basic approach.

3. In the figure below, square ABCD is attached to ΔADE as shown. If ∠EAD is equal to 30° and AE is equal to 4, then what is the area of square ABCD?

A.   8

A. 16

C. 64

D. 72

E. 64

Here’s How to Crack It

Start with Step 1: Know the question. Underline what is the area of square ABCD? Move to Step 2: Look at the answers. We don’t have any values for areas of other shapes within the figure, so there is nothing to Ballpark. But note the presence of and in the answers: They’re an additional clue, if you haven’t absorbed the info given, that either 30-60-90 and/or 45-45-90 triangles are in play.

The triangle in the figure is in fact a 30-60-90. Now move to Step 3: Break the problem into bite-sized pieces. Because angle A is the short angle, the side opposite that angle is equal to 4 and the hypotenuse is equal to 8. Now move on to Step 3a: Mark your figure with these values. Now move to Step 3b: Write down any formulas you need. The area for a square is s². Because that hypotenuse is also the side of the square, the area of the square must be 8 times 8, or 64. This is (C). If you forgot the ratio of the sides of a 30-60-90 triangle, go back and review it. You’ll need it.

POE Pointers

If you didn’t remember the ratio of the sides of a 30-60-90 triangle, could you have eliminated some answers using POE? Of course. Let’s see if we can use the diagram to eliminate some answer choices.

The diagram tells us that AE has length 4. Remember the important approximations we gave you earlier in the chapter? A good approximation for is 1.7. So 4 = approximately 6.8. We can now use this to estimate the sides of square ABCD. Just using your eyes, would you say that AD is longer or shorter than AE? Of course it’s a bit longer; it’s the hypotenuse of ΔADE. You decide and write down what you think it might be. To find the area of the square, simply square whatever value you decided the side equaled. This is your answer.

Now all you have to do is see which of the answer choices still makes sense. Could the answer be (A)? 8 equals roughly 13.6. Is this close to your answer? No way. Could the answer be (B), which is 16? Still much too small. Could the answer be (C), which is 64? Quite possibly. Could the answer be 72? It might be. Could the correct answer be 64? An approximation of = 1.4, so 64 equals 89.6. This seems rather large. Thus, on this problem, by using POE we could eliminate (A), (B), and (E).

FOUR-SIDED FIGURES

The interior angles of any four-sided figure (also known as a quadrilateral) add up to 360°. The most common four-sided figures on the ACT are the rectangle and the square, with the parallelogram and the trapezoid coming in a far distant third and fourth.

Your Friend the Triangle

Because a quadrilateral is really just two triangles, its interior angles must measure twice those of a triangle: 2(180) = 360.

A rectangle is a four-sided figure whose four interior angles are each equal to 90°. The area of a rectangle is base × height. Therefore, the area of the rectangle above is 8 (base) × 5 (height) = 40. The perimeter of a rectangle is the sum of all four of its sides. The perimeter of the rectangle above is 8 + 8 + 5 + 5 = 26.

A square is a rectangle whose four sides are all equal in length. You can think of the area of a square, therefore, as side squared. The area of the above square is 6 (base) × 6 (height) = 36. The perimeter is 24, or 4s.

A parallelogram is a four-sided figure made up of two sets of parallel lines. We said earlier that when parallel lines are crossed by a third line, eight angles are formed but that in reality there are only two—the big one and the little one. In a parallelogram, 16 angles are formed, but there are still, in reality, only two.

Geometry Hint

If there isn’t a figure, always draw your own.

The area of a parallelogram is also base × height, but because of the shape of the figure, the height of a parallelogram is not necessarily equal to one of its sides. Height is measured by a perpendicular line drawn from the base to the top of the figure. The area of the parallelogram above is 9 × 5 = 45.

D′oh, I’m in a Square!

To help you remember the area of a four-sided figure (a square, a rectangle, or a parallelogram), imagine that Bart and Homer Simpson are stuck inside of it. To get its area, just multiply Bart times Homer, or (b)(h), or the base times the height.

A trapezoid is a four-sided figure in which two sides are parallel. Both of the figures above are trapezoids. The area of a trapezoid is the average of the two parallel sides × the height, or (base 1 + base 2)(height), but on ACT problems involving trapezoids, there is almost always some easy way to find the area without knowing the formula (for example, by dividing the trapezoid into two triangles and a rectangle). In both trapezoids above, the area is 27.

CIRCLES

The distance from the center of a circle to any point on the circle is called the radius. The distance from one point on a circle through the center of the circle to another point on the circle is called the diameter. The diameter is always equal to twice the radius. In the circle on the left below, AB is called a chord. CD is called a tangent to the circle.

The curved portion of the right-hand circle between points A and B is called an arc. The angle formed by drawing lines from the center of the circle to points A and B is said to be subtended by the arc. There are 360° in a circle, so that if the angle we just mentioned equaled 60°, it would take up or of the degrees in the entire circle. It would also take up of the area of the circle and of the outer perimeter of the circle, called the circumference.

The formula for the area of a circle is πr².

The formula for the circumference is 2πr.

In the circle below, if the radius is 4, then the area is 16π, and the circumference is 8π.

The key to circle problems on the ACT is to look for the word or phrase that tells you what to do. If you see the word circumference, immediately write down the formula for circumference, and plug in any numbers the problem has given you. By solving for whatever quantity is still unknown, you have probably already answered the problem. Another tip is to find the radius. The radius is the key to many circle problems.

1. If the area of a circle is 16 square meters, what is its radius in meters?

A.

B. 12π

C.

D.

E. 144π²

Here’s How to Crack It

Step 1: Know the question. We need to solve for the radius. Step 2: Let the answers help. We don’t have a figure, so there’s nothing to Ballpark. But no figure? Step 3a: Draw your own.

Step 3b: Write down any formulas you need and fill in the information you have. Set the formula for area of a circle equal to πr² = 16. The problem is asking for the radius, so you have to solve for r. If you divide both sides by π, you get

The correct answer is (C).

2. In the figure below, the circle with center O is inscribed inside square ABCD as shown. If a side of the square measures 8 units, what is the area of the shaded region?

F.   8 − 16π

G.   8π

H. 64 − 16π

J. 64 − 8π

K. 64π

Here’s How to Crack It

Begin with Step 1, and underline what is the area of the shaded region? Step 2 brings us to the answers, and we see all of the answers have π in them. Since π is approximately 3, (F) would be a negative area. Eliminate this answer. If no other answer choice can be obviously eliminated via Ballparking, move to Step 3. Break the problem into bite-sized pieces, but don’t get hung up on “inscribed.” Yes, that’s an important term to know, but since we have the figure, it’s irrelevant. Move to Step 3a and 3b: Mark the side of the square “8,” and write down the formulas for the area of a circle and square: πr² and s².

Is there a formula for the shape made by the shaded region? Nope. We just need the basic formulas for the basic shapes. 8² = 64, so we at least know the shaded region is less than 64, the area of the square. At this point we know that the answer must be 64 minus the area of the circle, so we can eliminate (G) and (K) because they do not match this format. What’s the link between the square and the circle? The side of the square equals the diameter. So if the diameter is 8, then the radius must be 4. Use that in the area formula: 4² π = 16π. Subtract the area of the circle from the area of the square, and we get (H).

FUN FACTS ABOUT FIGURES

Read and review the following facts you need to know about plane geometry.

Angle Facts

• There are 90° in a right angle.

• When two straight lines intersect, the angles opposite each other are equal.

• There are 180° in a straight line.

• Two lines are perpendicular when they meet at a 90° angle.

• The sign for perpendicular is ⊥.

• Bisect means to cut exactly in half.

• There are 180° in a triangle.

• There are 360° in any four-sided figure.

Triangle Facts

In any triangle

• The longest side is opposite the largest angle.

• The shortest side is opposite the smallest angle.

• All angles add up to 180°.

• Area = (base × height) = bh

• The height is the perpendicular distance from the base to the opposite vertex.

• Perimeter is the sum of the sides.

• The third side of any triangle is always less than the sum and greater than the difference of the other two sides.

In an isosceles triangle

• Two sides are equal.

• The two angles opposite the equal sides are also equal.

In an equilateral triangle

• All three sides are equal.

• All angles are each equal to 60°.

Four-Sided Figure Facts

In a quadrilateral

• All four angles add up to 360°.

In a parallelogram

• Opposite sides are parallel and equal.

• Opposite angles are equal.

• Adjacent angles are supplementary (add up to 180°).

• Area = base × height = bh

• The height is the perpendicular distance from the base to the opposite side.

In a rhombus

• Opposite sides are parallel.

• Opposite angles are equal.

• Adjacent angles are supplementary (add up to 180°).

• All 4 sides are equal.

• Area = base × height = bh

• The height is the perpendicular distance from the base to the opposite side.

• The diagonals are perpendicular.

In a rectangle

• Rectangles are special parallelograms; thus, any fact about parallelograms also applies to rectangles.

• All 4 angles are each equal to 90°.

• Area = length × width = lw

• Perimeter = 2(length) + 2(width) = 2l + 2w

• The diagonals are equal.

In a square

• Squares are special rectangles; thus, any fact about rectangles also applies to squares.

• All 4 sides are equal.

• Area = (side)² = s²

• Perimeter = 4(side) = 4s

• The diagonals are perpendicular.

Circle Facts

Circle

• There are 360° in a circle.

Radius (r)

• The distance from the center to any point on the edge of the circle.

• All radii in a circle are equal.

Diameter (d)

• The distance of a line that connects two points on the edge of the circle, passing through the center.

• The longest line in a circle.

• Equals twice the radius.

Chord

• Any line segment connecting two points on the edge of a circle.

• The longest chord is called the diameter.

Circumference (C)

• The distance around the outside of the circle.

• C = 2πr = πd

Arc

• Any part of the circumference.

• The length of an arc is proportional to the size of the interior angle.

Area

• The amount of space within the boundaries of the circle.

• A = πr²

Sector

• Any part of the area formed by two radii and the outside of the circle.

• The area of a sector is proportional to the size of the interior angle.

Line Facts

Line

• A line has no width and extends infinitely in both directions.

• Any line measures 180°.

• A line that contains points A and B is called (line AB).

• If a figure on the ACT looks like a straight line, and that line looks like it contains a point, it does.

Ray

• A ray extends infinitely in one direction but has an endpoint.

• The degree measure of a ray is 180°.

• A ray with endpoint A that goes through point B is called . Pay attention to the arrow above the points and the order they are given; those will determine the direction the ray is pointing!

Line Segment

• A line segment is a part of a line and has two endpoints.

• The degree measure of a line segment is 180°.

• A line segment, which has endpoints of A and B, is written as AB.

Tangents

• Tangent means intersecting at one point. For example, a line tangent to a circle intersects exactly one point on the circumference of the circle. Two circles that touch at just one point are also tangent.

• A tangent line to a circle is always perpendicular to the radius drawn to that point of intersection.

• If AB intersects a circle at point T, then you would say, “AB is tangent to the circle at point T.”

PLANE GEOMETRY FORMULAS

Here’s a list of all the plane geometry formulas that could show up on the ACT. Memorize the formulas for perimeter/circumference, area, and volume for basic shapes. ACT usually provides the more advanced formulas if they are needed.

You won’t be able to take any notes into the test with you, so it’s a good idea to make sure you know these formulas by heart!

Circles

• Area: A = πr²

• Circumference: C = 2πr = πd

Triangles

• Area: A bh

• Perimeter: P = sum of the sides

• Pythagorean theorem: a² + b² = c²

SOHCAHTOA

• 

• 

• 

• 

• 

• 

Quadrilaterals

Parallelograms

• Area: A = bh

• Perimeter: P = sum of the sides

Rhombus

• Area: A = bh

• Perimeter: P = sum of the sides

Trapezoids

• Area: A = h (b₁ + b₂)

• Perimeter: P = sum of the sides

Rectangles

• Area: A = lw

• Perimeter: P = 2(l + w)

Squares

• Area: A = s²

• Perimeter: P = 4s

Polygons

• Sum of angles in an n-sided polygon: (n − 2) 180°

• Angle measure of each angle in a regular n-sided polygon:

3-D Figures

• Surface area of a rectangular solid: S = 2(lw + lh + wh)

• Surface area of a cube: S = 6s²

• Surface area of a right circular cylinder: S = 2πr² + 2πrh

• Surface area of a sphere: S = 4πr²

• Volume of a cube: V = s³

• Volume of a rectangular solid: V = lwh

• Volume of a right circular cylinder: V = πr²h

• Volume of a sphere: V =

GLOSSARY

Arc:	Any part of the circumference
Bisect:	To cut in half
Chord:	Any line segment connecting two points on the edge of a circle
Circumscribed:	Surrounded by a circle as small as possible
Collinear:	Lying on the same line
Congruent:	Equal in size
Diagonal (of a polygon):	A line segment connecting opposite vertices
Equilateral triangle:	All sides are equal and each angle measures 60°
Inscribed (angle in a circle):	An angle in a circle with its vertex on the circumference
Isosceles triangle:	A triangle with two equal sides
Parallel:	Two distinct lines that do not intersect
Perpendicular:	At a 90° angle
Plane:	A flat surface extending in all directions
Polygon:	A closed figure with two or more sides
Quadrilateral:	A four-sided figure
Regular polygon:	A figure with all equal sides and angles
Sector:	Any part of the area formed by two radii and the outside of the circle
Similar:	Equal angles and proportional sides
Surface area:	The sum of areas of each face of a figure
Tangent:	Intersecting at one point
Vertex/Vertices:	A corner point. For angles, it’s where two rays meet. For figures, it’s where two adjacent sides meet.

Geometry Drill

For the answers to this drill, please go to Chapter 25.

1. In ΔABC below, ∠A = ∠B, and ∠C is twice the measure of ∠B. What is the measure, in degrees, of ∠A ?

A. 30

B. 45

C. 50

D. 75

E. 90

2. In the figure below, l₁ ∥ l₂. Which of the labeled angles must be equal to each other?

F. A and C

G. D and E

H. A and B

J. D and B

K. C and B

3. In the figure below, right triangles ABC and ACD are drawn as shown below. If AB = 20, BC = 15, and AD = 7, then CD = ?

A. 21

B. 22

C. 23

D. 24

E. 25

4. If the area of circle A is 16π, then what is the circumference of circle B if its radius is that of circle A ?

F.   2π

G.   4π

H.   6π

J.    8π

K. 16π

5. In the figure below, MO is perpendicular to LN, LO is equal to 4, MO is equal to ON, and LM is equal to 6. What is MN ?

A. 2

B. 3

C. 4

D. 3

E. 6

Summary

• Use the basic approach.

  • Step 1: Know the question. Read the whole problem before calculating anything, and underline the actual question.

  • Step 2: Let the answers help. Look for clues on how to solve and ways to use Process of Elimination (POE). Ballparking works well on geometry questions on area and angles.

  • Step 3: Break the problem into bite-sized pieces. When you read the problem a second time, calculate at each step necessary and watch out for tricky phrasing. On geometry, this means

    • Step 3a: Write all the information given in the problem on the figure. If there is no figure, draw your own.

    • Step 3b: Write down any formulas you need and fill in any information you have.

• There are several things to know about angles and lines.

  • A line is a 180° angle.

  • When two lines intersect, four angles are formed, but in reality there are only two distinct measures.

  • When two parallel lines are cut by a third line, eight angles are formed, but in reality there are still only two (a large one and a small one).

• There are several things to know about triangles.

  • A triangle has three sides and three angles; the sum of the angles equals 180°.

  • An isosceles triangle has two equal sides and two equal angles opposite those sides.

  • An equilateral triangle has three equal sides and three equal angles; each angle equals 60°.

  • A right triangle has one 90° angle. In a right triangle problem, you can use the Pythagorean Theorem to find the lengths of sides.

  • Some common right triangles are 3-4-5, 6-8-10, 5-12-13, and 7-24-25.

  • ACT test writers also like the isosceles right triangle, in which the sides are always in the ratio s: s: s, and the 30-60-90 triangle, in which the sides are always in the ratio s: s : 2s.

  • Similar triangles have the same angle measurements and sides that are in the same proportion.

  • The area of a triangle is equal to , with height measured perpendicular to the base.

• Four-sided objects are called quadrilaterals and have four angles, which add up to 360°. There are several important things to remember.

  • The area of a rectangle, a square, or a parallelogram can be found using the formula base × height = area, with height measured perpendicular to the base.

  • The perimeter of any object is the sum of the lengths of its sides.

  • The area of a trapezoid is equal to the average of the two bases times the height.

• For any circle problem, you need to know four basic things.

  • Radius

  • Diameter

  • Area (πr²)

  • Circumference (πd or 2πr)

• Don’t forget that you can plug in on geometry questions that have variables in the answer choices.