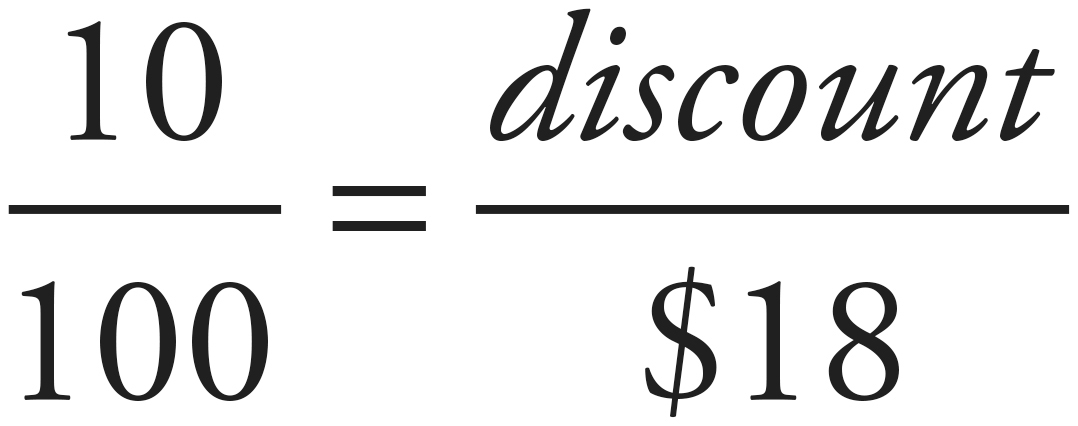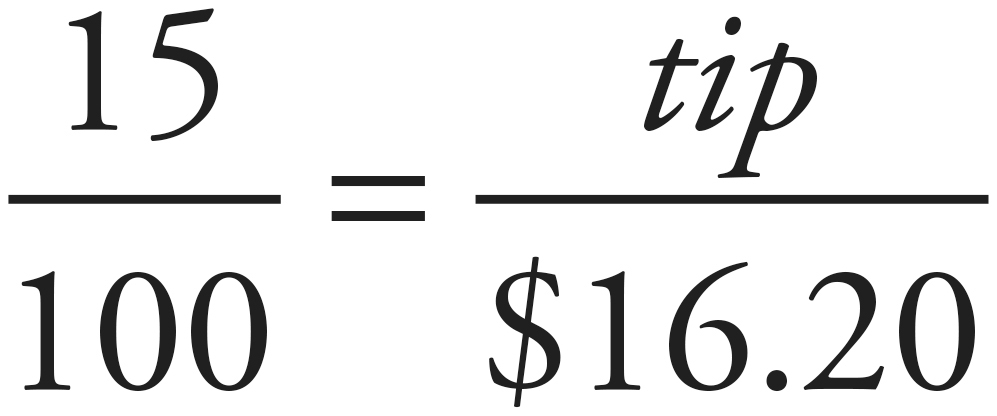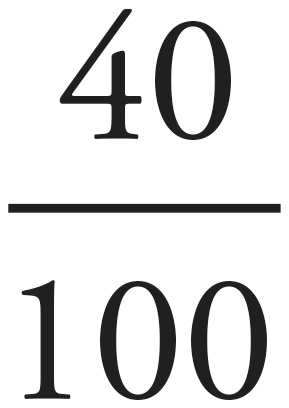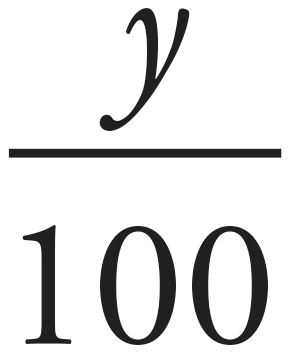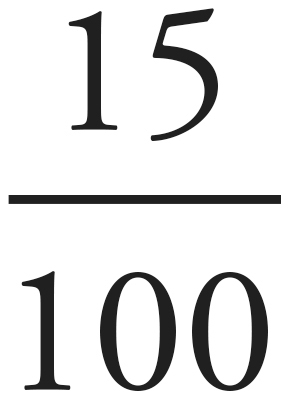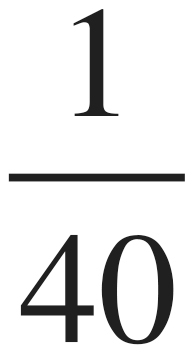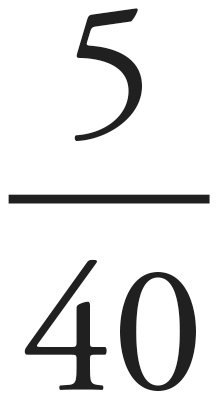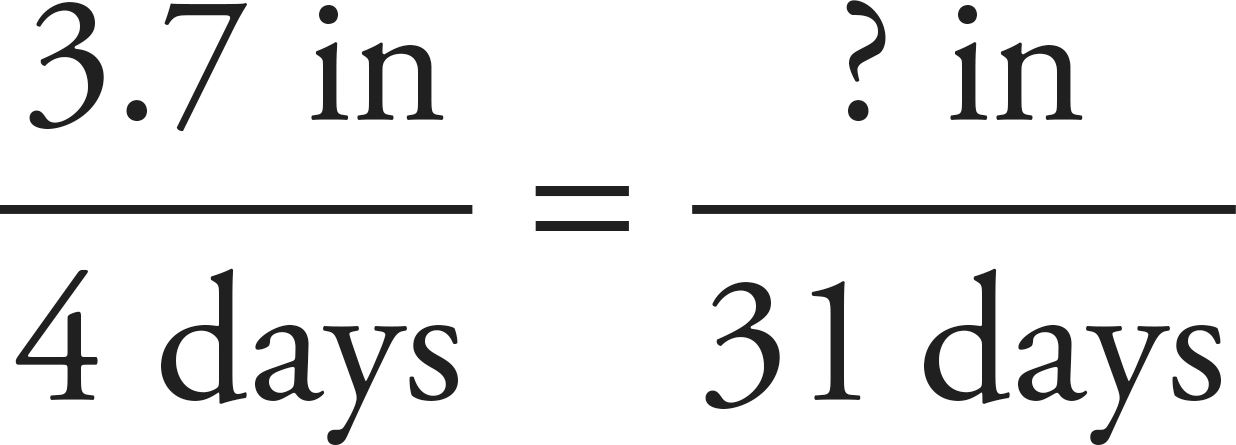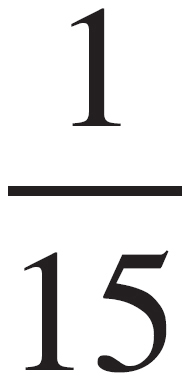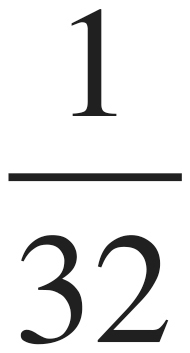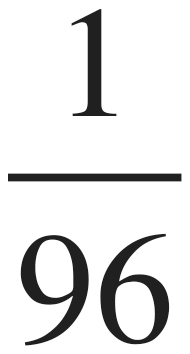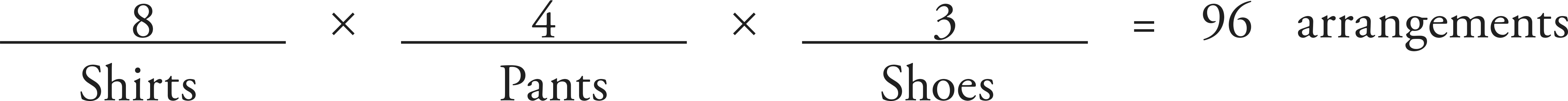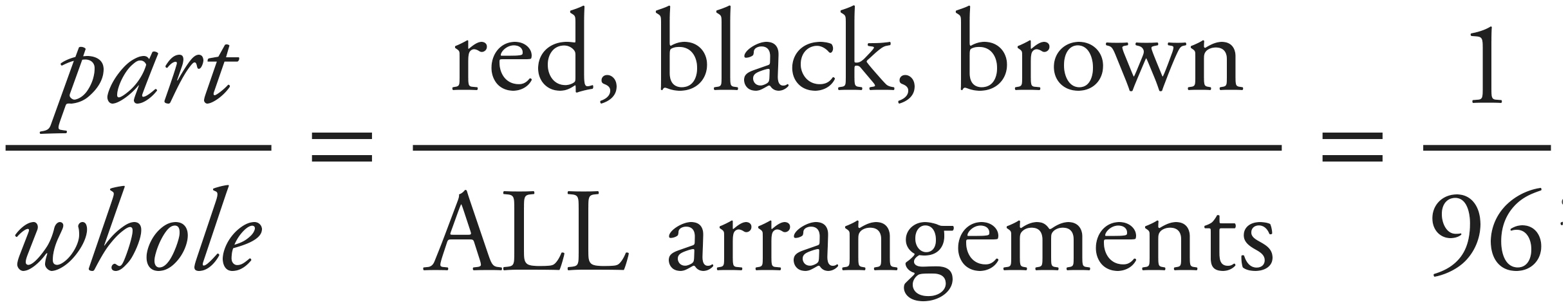Now that you’ve refreshed some of the essential geometry concepts, we will see how to integrate those concepts with your test-taking strategy. In addition, we’ll see some other Word Problem strategies that will help you to complete problems quickly and accurately.
Remember what the main requirements are for a Plugging In problem. You need variables in the answer choices or question: That’s it. It doesn’t say anywhere that the problem needs to be a pure algebra problem. What is a pure algebra problem anyway? Don’t forget: Part of what makes this test so hard is that ACT piles concept on top of concept in its problems. In other words, geometry problems often are algebra problems.
We prefer a simple definition of a word problem: It has to tell a story. But as we discussed in Chapter 12, plug-and-chug geometry questions can have so much information in them that they feel like word problems. So treat them like word problems, and let’s refresh the basic approach we discussed in Chapter 12.
Know the question. Read the whole problem before calculating anything, and underline the actual question.
Let the answers help. Look for clues on how to solve and ways to use POE.
Break the problem into bite-sized pieces. When you read the problem a second time, calculate at each step necessary and watch out for tricky phrasing.
For geometry questions, Step 3 has two specific additions:
Step 3a: Write all the information given in the problem on the figure. If there is no figure, draw your own.
Step 3b: Write down any formulas you need and fill in any information you have.
Let’s look at a short, straightforward example.
1. A circle with center O has a radius r. What is the area of a circle with a radius three times larger?
A. 3πr
B. 9πr
C. 3πr2
D. 6πr2
E. 9πr2
Here’s How to Crack It
Step 1: Know the question. We need to find the area of this new larger circle, not the larger radius.
Step 2: Let the answers help. First of all, we’re looking for the area, which means something will have to be squared, so we can eliminate (A) and (B), which can’t be right. Now, notice that each of these answer choices has a variable in it. If you’re thinking Plugging In, you’re thinking right.
Step 3: Break the problem into bite-sized pieces. Let’s pick an easy value for r, like r = 2.
Step 3a: Write all the information given in the problem on the figure. There’s no figure here, so draw 2 circles.
Step 3b: Write down any formulas you need and fill in any information you have. The formula for the area of a circle that we’ll need is A = πr2.
If the original radius is 2, then the larger radius, which is three times larger, must be 6. Therefore, the area of the larger circle must be A = π(6)2 = 36π. We’ve got a target answer, so let’s try it in the answer choices. Remember, we’ve already eliminated (A) and (B).
A. 3πr
B. 9πr
C. 3π(2)2 = 12π 
D. 6π(2)2 = 24π 
E. 9π(2)2 = 36π 
Choice (E) is the correct answer. Have another look at those answer choices and think of all the ways you could make mistakes on this problem. Plugging In saves the day again by minimizing the possibility for algebra errors.
When it comes to writing word problems, ACT test writers can draw on both algebra and geometry, as we’ve seen. But lots of word problems, and even some plug-and-chugs, will test a variety of arithmetic concepts. The rest of this chapter will review those topics.
Percentages, probabilities, and ratios can get mighty complex in your math classes at school. Do you want the good news or the bad news? Well, the bad news is that ratios, percentages, and probabilities will all appear on the ACT Math test, but the good news is that they’re all testing the same basic concept: parts to wholes.
Let’s say you’re taking batting practice. You are thrown 100 pitches and hit 20 of them. Ignoring the fact that you’re probably not ready for the MLB, let’s put this into some math language. Once we get the basics down, we’ll try some more advanced problems.
First, what percentage of the pitches did you hit? Well, that’s easy on this one because we’re dealing with 100. But you can always find percentages with this simple part-to-whole formula:
Once we put the numbers in, we’ll get this: 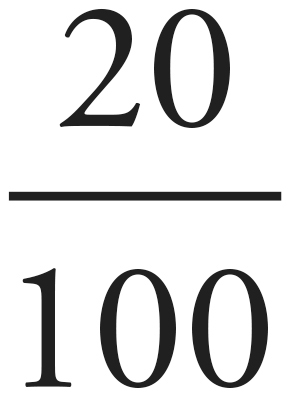 × 100% = 0.2 × 100% = 20%. If you hit 20 of the 100 pitches, you hit 20% of them.
× 100% = 0.2 × 100% = 20%. If you hit 20 of the 100 pitches, you hit 20% of them.
Next, what is the probability that you were to hit any given pitch? Remember, this is just a matter of parts to wholes, so we can find this probability as follows:  =
=  =
= 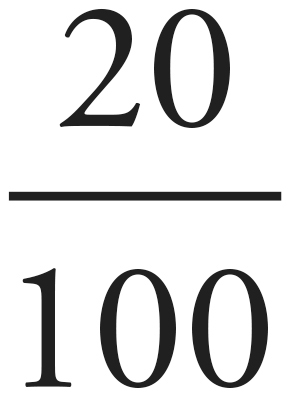 = 0.2. In other words, there’s a 0.2, or
= 0.2. In other words, there’s a 0.2, or  , probability you hit any given pitch during batting practice.
, probability you hit any given pitch during batting practice.
Ratios are a little different. Usually these will ask for the relationship of some part to some other part. If we’re still using our batting practice statistics, we might want to know something like, what’s the ratio of the pitches you hit to the pitches you missed?
Even though we’re not dealing with the whole this time, we’ll find the ratio the same way, but instead of  , we’ll use
, we’ll use  =
= 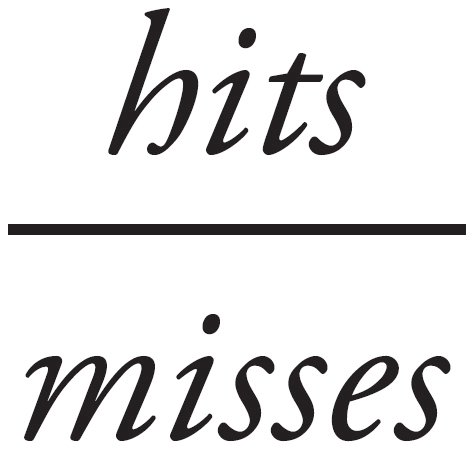 =
= 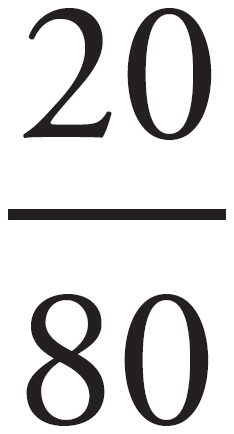 =
=  . The ratio of hits to misses is
. The ratio of hits to misses is  , or 1 to 4, or 1:4.
, or 1 to 4, or 1:4.
If it feels like we just did the same thing three times, it was supposed to. As we’ve seen a few times already, just because things have different names doesn’t mean that they are unrelated. Let’s try some problems.
1. At a restaurant, diners enjoy an “early bird” discount of 10% off their bills. If a diner orders a meal regularly priced at $18 and leaves a tip of 15% of the discounted meal (no tax), how much does he pay in total?
A. $13.50
B. $16.20
C. $18.63
D. $18.90
E. $20.70
Here’s How to Crack It
Step 1: Know the question. We want the price of the discounted meal plus tip.
Step 2: Let the answers help. We are reducing a number by 10%, then increasing it by 15%, so it’s not likely that the final number will be much less or much greater than $18. Let’s eliminate (A) and (E).
Step 3: Break the problem into bite-sized pieces.
First, we’ll need to figure out what the discounted price of the meal is. There are a number of ways to do this, but if you find this  method useful, you could find the discount this way:
method useful, you could find the discount this way:
10% = discount
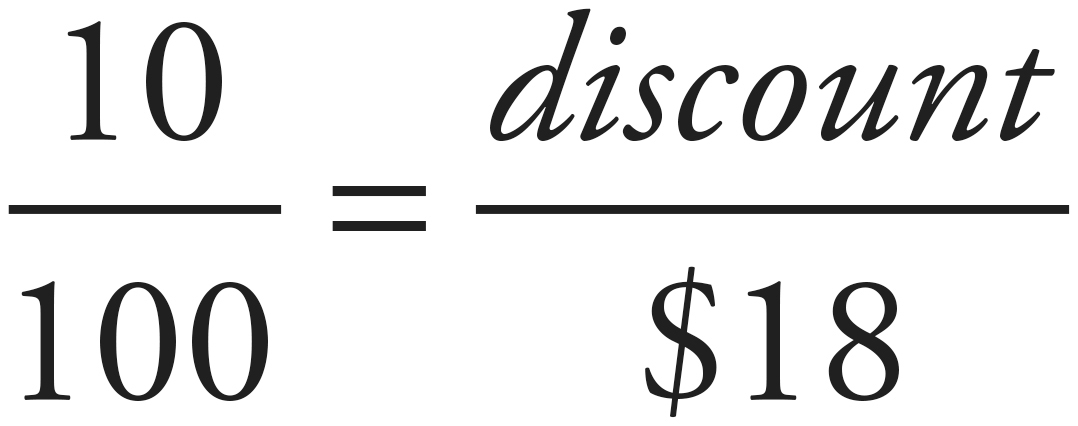
discount = $1.80
The price of the discounted meal, then, is $18 − $1.80 = $16.20. Let’s find the tip the same way.
15% = tip
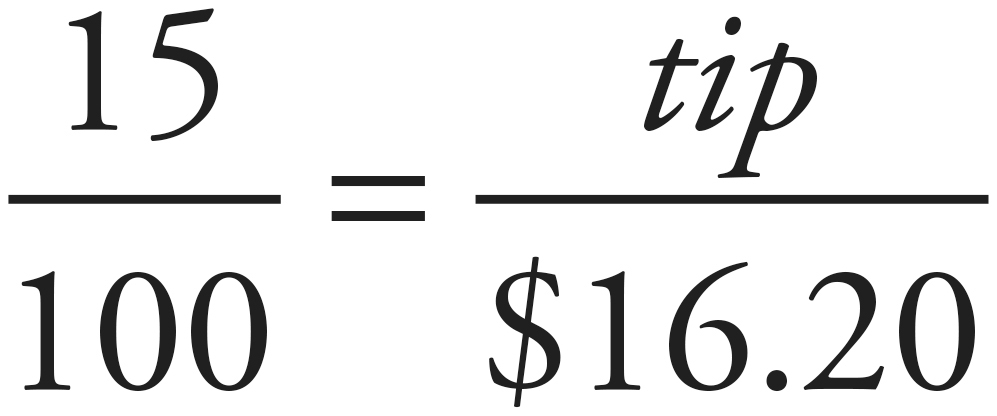
tip = $2.43
The price of the discounted meal plus tip, therefore, is $16.20 + $2.43 = $18.63. The correct answer is (C).
A percentage is a fraction in which the denominator equals 100. In literal terms, the word percent means “divided by 100,” so any time you see a percentage in an ACT question, you can punch it into your calculator quite easily. If a question asks for 40 percent of something, for instance, you can express the percentage as a fraction: 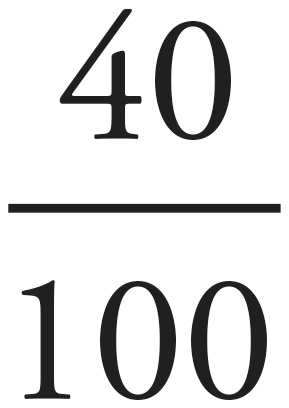 . Any time you are looking for a percent, you can use your calculator to find the decimal equivalent and multiply the result by 100. If four out of five dentists recommend a particular brand of toothpaste, you can quickly determine the percent of doctors who recommend it by typing
. Any time you are looking for a percent, you can use your calculator to find the decimal equivalent and multiply the result by 100. If four out of five dentists recommend a particular brand of toothpaste, you can quickly determine the percent of doctors who recommend it by typing  × 100 and hitting the ENTER key. The resulting “80” just needs a percent sign tacked onto it. To properly translate all percent questions, it is helpful to have a decoding table for the various terms you’ll come across.
× 100 and hitting the ENTER key. The resulting “80” just needs a percent sign tacked onto it. To properly translate all percent questions, it is helpful to have a decoding table for the various terms you’ll come across.
|
English
|
Math Equivalent
|
|
percent
|
/100
|
|
of
|
multiplication (×)
|
|
what
|
variable (y, z)
|
|
is, are, were
|
=
|
|
what percent
|
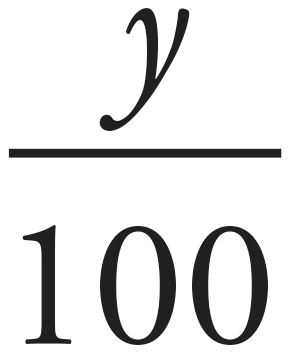
|
In the last problem, we could have saved a little time if we had realized that  = 20 percent. Therefore,
= 20 percent. Therefore,  would be 4 × 20 percent, or 80 percent. On the next page you’ll find some fractions and decimals whose percent equivalents you should know.
would be 4 × 20 percent, or 80 percent. On the next page you’ll find some fractions and decimals whose percent equivalents you should know.
Another fast way to do percents is to move the decimal place. To find 10 percent of any number, move the decimal point of that number over one place to the left.
10% of 500 = 50
10% of 50 = 5
10% of 5 = .5
To find 1 percent of a number, move the decimal point of that number over two places to the left.
1% of 500 = 5
1% of 50 = 0.5
1% of 5 = 0.05
You can use a combination of these last two techniques to find even very complicated percentages by breaking them down into easy-to-find chunks.
-
20% of 500: 10% of 500 = 50, so 20% is twice 50, or 100.
-
30% of 70: 10% of 70 = 7, so 30% is three times 7, or 21.
-
32% of 400: 10% of 400 = 40, so 30% is three times 40, or 120.
-
1% of 400 = 4, so 2% is two times 4, or 8.
Therefore, 32 percent of 400 = 120 + 8 = 128.
 = 0.2 = 20%
= 0.2 = 20%
 = 0.25 = 25%
= 0.25 = 25%
 = 0.33 = 33
= 0.33 = 33 %
%
 = 0.5 = 50%
= 0.5 = 50%
Let’s have a look at another ACT percentage problem.
2. When 15% of 40 is added to 5% of 260, the resulting number is:
F. 19
G. 40
H. 95
J. 180
K. 260
Here’s How to Crack It
Let’s try this one using the decoding table. Although this isn’t really a word problem, that doesn’t mean we shouldn’t be careful and break it into bite-sized pieces.
First, 15% of 40. Remember, % translates to divide by 100, and “of” translates to multiplication. Therefore, we can rewrite 15% of 40 as 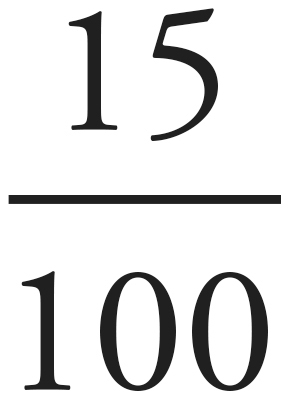 × 40. Put this expression in your calculator to find that
× 40. Put this expression in your calculator to find that 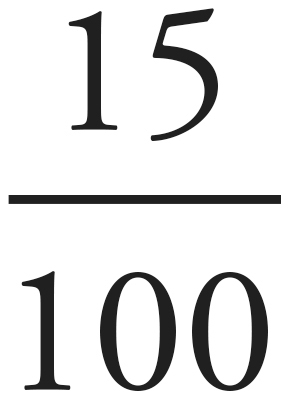 × 40 = 6.
× 40 = 6.
Now, find 5% of 260. Use the same translations to find  × 260 = 13. We’ve done the tough part, so let’s substitute what we’ve found back into the problem: When 6 is added to 13, the resulting number is: Now that’s a problem we can handle! 6 + 13 = 19, so the answer is (F).
× 260 = 13. We’ve done the tough part, so let’s substitute what we’ve found back into the problem: When 6 is added to 13, the resulting number is: Now that’s a problem we can handle! 6 + 13 = 19, so the answer is (F).
3. Herbie’s practice bag contains 4 blue racquetballs, one red racquetball, and 6 green racquetballs. If he chooses a ball at random, which of the following is closest to the probability that the ball will NOT be green?
A. 0.09
B. 0.27
C. 0.36
D. 0.45
E. 0.54
Here’s How to Crack It
Step 1: Know the question. Make sure you read carefully! We want the probability that the chosen ball will NOT be green.
Step 2: Let the answers help. Green balls account for slightly more than half the number of balls in the bag, so the likelihood that the ball will NOT be green should be slightly less than half. That eliminates (A), (B), and (E). Not bad!
Step 3: Break the problem into bite-sized pieces. This is a pretty straightforward  problem:
problem:  =
=  =
=  . The only slight difficulty is that the answers are not listed as fractions, but it’s nothing a calculator can’t help. Find 5 ÷ 11 = 0.45, (D).
. The only slight difficulty is that the answers are not listed as fractions, but it’s nothing a calculator can’t help. Find 5 ÷ 11 = 0.45, (D).
4. If the ratio of 2x to 5y is  , what is the ratio of x to y ?
, what is the ratio of x to y ?
F. 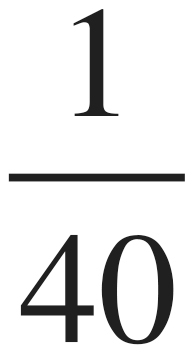
G. 
H. 
J. 
K. 
Here’s How to Crack It
The difficulty of this problem is all in the setup. Just remember that you’re comparing parts to wholes, and you’ll be fine.
To isolate  on the left side of this equation, let’s multiply both sides of the equation by
on the left side of this equation, let’s multiply both sides of the equation by  .
.
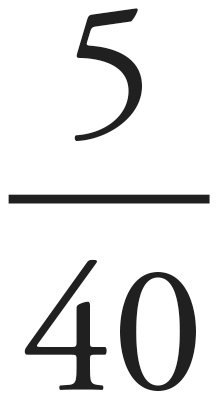 reduces to
reduces to  . The answer is (J).
. The answer is (J).
If you got stuck on this one, look at those answer choices: You could’ve used PITA!
Let’s see how ACT might test ratios in a word problem.
5. If 3.7 inches of rain fell on Vancouver during the first 4 days of December, and the rain continues to fall at this pace for the rest of the month, approximately how many feet of rain will fall during December? (Note: The month of December has 31 days.)
A. 2.4
B. 3.7
C. 9.5
D. 28.7
E. 114.7
Here’s How to Crack It
Step 1: Know the question. It’s in the last line: how many feet of rain will fall in December? But be careful: The value given in the problem is in inches. We’re going to have to do some converting!
Step 2: Let the answers help. Since we know the problem is asking how many feet of rain will fall, and the problem tells us that 3.7 inches of rain will fall in 4 days, we can do some Ballparking. The number of inches will increase, but it will be reduced again when we convert it into feet. Choice (E) is definitely too big, and (D) probably is too.
Step 3: Break the problem into bite-sized pieces. There are going to be two main parts to this problem: First, we want to figure out how much rain will fall in 31 days, then we want to convert it to feet. We can do this by using ratios.
The ratio given in the problem is 3.7 inches every four days, or in math terms,  . The ratio will remain the same no matter how many days there are, so let’s use this ratio to find how many inches of rain will fall in December.
. The ratio will remain the same no matter how many days there are, so let’s use this ratio to find how many inches of rain will fall in December.
We can rearrange the terms to find
But we can’t stop here! Remember, the problem is asking for a value in feet. (It’s a good thing we did some early POE, isn’t it?)
We’ll use the same process, and this time we already know the ratio of inches to feet:  . As we did above, let’s use this ratio to find our answer.
. As we did above, let’s use this ratio to find our answer.
Rearrange the equation to find
There are only three parts to any average question. Fortunately for you, the ACT must give you two of these parts, which are all you need to find the third. The average pie is an easy way to keep track of the information you get from questions dealing with averages. If you have the total, you can always divide by either the average or the number of things in the set (whichever you are given) to find the missing piece of the pie. Similarly, if you have the number of things and the average, you can multiply the two together to arrive at the total (the sum of all the items in the set).
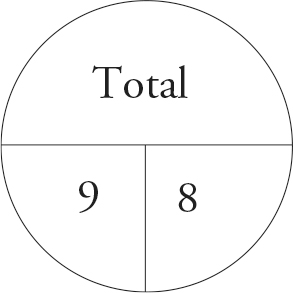
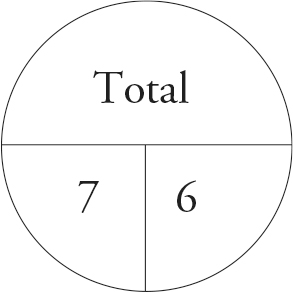
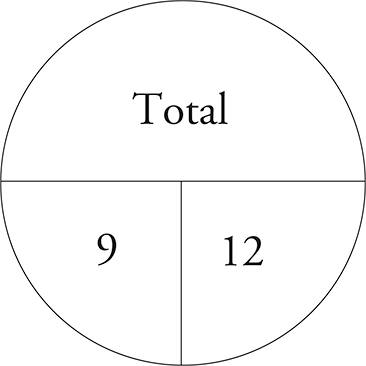
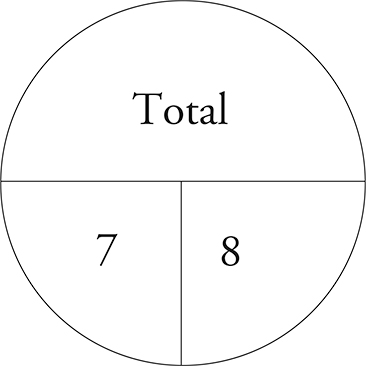
For example, if you want to find the average of 9, 12, and 6 using the average pie, you know you have 3 items with a total of 27. Dividing the total, 27, by the number of things, 3, will yield the average, 9. Your pie looks like this:
Arithmetic mean—just a fancy way of saying “average.”
Median—the one in the middle, like the median strip on the highway.
Mode—you’re looking for the element that appears most. Get it? MOde, MOst.
Although you probably could have done that without the average pie, more difficult average questions involve multiple calculations and lend themselves particularly well to using the pie. Let’s take a look at one:
3. Over 9 games, a baseball team had an average of 8 runs per game. If the average number of runs for the first 7 games was 6 runs per game and the same number of runs was scored in each of the last 2 games, how many runs did the team score during the last game?
A. 5
B. 15
C. 26
D. 30
E. 46
Here’s How to Crack It
Step 1: Know the question. How many runs did the team score during the last game?
Step 2: Let the answers help. Eliminate (A). Even though the average for the first 7 is higher than all 9, the runs scored in the last two games can’t be that few. Similarly, (E) is probably too big. If you don’t trust your sense of numbers and you’re not comfortable Ballparking here, however, leave both. It’s a complicated question on a more advanced topic.
Step 3: Break the problem into bite-sized pieces. Let’s use bite-size pieces to put the information from the first line of this problem into our trusty average pie.
What is the sum of everything for these 9 games? 9 × 8, or 72.
Now let’s put the information from the second line into the average equation.
What is the sum of everything for these 7 games? 7 × 6, or 42.
If all 9 games added up to 72 and 7 of these games added up to 42, then the remaining 2 games added up to 72 − 42, or 30. In case you are feeling smug about getting this far, the ACT writers made 30 the answer for (D).
But of course you know that they only want the runs they scored in the last game. Because the same number of runs was scored in each of the last two games, the answer is  or 15, (B).
or 15, (B).
ACT writers have a particular fondness for “weighted average” problems. First, let’s look at a regular unweighted average question.
If Sally received a grade of 90 on a test last week and a grade of 100 on a test this week, what is her average for the two tests?
Piece of cake, right? The answer is 95. You added the scores and divided by 2. Now let’s turn the same question into a weighted average question.
If Sally’s average for the entire year last year was 90 and her average for the entire year this year was 100, is her average for the two years combined equal to 95 ?
The answer is “not necessarily.” If Sally took the same number of courses in both years, then yes, her average is 95. But what if last year she took 6 courses, while this year she took only 2 courses? Can you compare the two years equally? ACT likes to test your answer to this question. Here’s an example.
1. The starting team of a baseball club has 9 members who have an average of 12 home runs apiece for the season. The second-string team for the baseball club has 7 members who have an average of 8 home runs apiece for the season. What is the average number of home runs for the starting team and the second-string team combined?
A. 7.5
B. 8
C. 10
D. 10.25
E. 14.2
Here’s How to Crack It
The ACT test writers want to see whether you spot this as a weighted average problem. If you thought the first-string team was exactly equivalent to the second-string team, then you merely had to take the average of the two averages, 12 and 8, to get 10. In weighted average problems, the ACT test writers always include the average of the two averages among the answer choices, and it is always wrong. 10 is choice (C). Cross off (C).
The two teams are not equivalent because there are different numbers of players on each team. To get the true average, we’ll have to find the total number of home runs and divide by the total number of players. How do we do this? By going to the trusty average formula as usual. The first line of the problem says that the 9 members on the first team have an average of 12 runs apiece.
So the sum of everything is 9 × 12, or 108.
The second sentence says that the 7 members of the second team have an average of 8 runs each.
So the total is 7 × 8, or 56.
Now we can find the true average. Add all the runs scored by the first team to all the runs scored by the second team: 108 + 56 = 164. This is the true total. We divide it by the total number of players (9 + 7 = 16).
The answer is 10.25, or (D).
Since calculators were added to the arsenal you’re allowed to bring with you when you take the ACT, more and more of the test has been composed of questions on which calculators are of little or no use, such as questions based on charts and graphs. On this type of question, your math skills aren’t really being tested at all; what ACT is interested in is your ability to read a simple graph (not unlike on the Science Reasoning test, which we’ll get to later in Part V). All of the questions we have seen in this format have been very direct. If you can read a simple graph, you can always get them right. What’s most important on questions like these is paying attention to the labels on the information. Let’s take a look at a graph.
23. Between which two months was the change in total rainfall the greatest?
A. May and June
B. June and July
C. July and August
D. August and September
E. September and October
Here’s How to Crack It
The ACT test writers want to see if you can decipher the information presented in the graph. Before you read the question then, you need to take a look at the graph. What is measured here? It says on the bottom: Average monthly rainfall in Belleville, IL. You should look at the values along the left side and bottom of the graph as well. When you do, you’ll see that the rain is measured in inches (left-hand side), and the measurements were made each month (bottom).
Now for the question. To determine which two months had the greatest change, we need to compare the change between each pair of months, discarding the smaller ones until we have only one left. The difference from May to June is about 3, and that’s larger than June to July and September to October, so (B) and (E) are out. July to August is larger still, though, so (A) is out, leaving only (C) and (D). It should be pretty apparent that the August to September change is larger than the July to August change, though, so the correct answer must be (D).
Although most questions involving graphs on the Math test are this simple, you may see slightly more complicated variations. Here’s another question based on the same bar graph.
24. Based on the information presented in the graph below, what is the approximate average monthly rainfall in Belleville, IL, for the period given?
F. 2
G. 3
H. 4
J. 5
K. 8
Here’s How to Crack It
As with the last question, the first thing you want to do is examine the graph and figure out what information is being given to you and how it is being presented. Because you already did that for this graph, we’ll skip that step on this one.
This question combines graph reading with average calculation, so the next thing you’ll have to do is estimate the rainfall for each month. Because the question uses the word approximate, you don’t have to worry too much about making super-exact measurements of the heights of the bar graphs. Eyeballing it and rounding to the closest value given on the left-hand side will be good enough to get you the right answer. Do that now before you read the next sentence.
To us, it looks like about 2 inches fell in May and September, and around 3 fell in October. July saw about 4, June roughly 5, and August about 8. Your estimates should be the same as ours. If they’re not, go back now and figure out why not. You probably need to be a little more careful in your estimating. Use another piece of paper as a guide if necessary (you can use your answer sheet in this manner when taking the real ACT).
Now it’s just a matter of calculating the average. Find the total first.
2 + 2 + 3 + 4 + 5 + 8 = 24
There are 6 months, so divide the total by 6 to find the average.
So the answer is 4, or (H).
Combination problems ask you how many different ways a number of things could be chosen or combined. The rules for combination problems on the ACT are straightforward.
-
Figure out the number of slots you need to fill.
-
Fill in those slots.
-
Find the product.
Seem confusing? It’s not. Let’s look at an example. This is what most combination problems on the ACT will look like:
6. At the school cafeteria, students can choose from 3 different salads, 5 different main dishes, and 2 different desserts. If Isabel chooses one salad, one main dish, and one dessert for lunch, how many different lunches could she choose?
F. 10
G. 15
H. 25
J. 30
K. 50
Here’s How to Crack It
We’ve got three slots to fill here, one for each item: salad, main dish, dessert. And the number of possibilities for each is pretty clear. Set up the slots and take the product as your answer.
The correct answer here is (J).
On a more difficult problem, you may run into a combination with more restricted elements. Just be sure to read the problem carefully before attempting it. If the question makes your head spin, leave it and return to it later, or pick your Letter of the Day and move on. For good measure, though, here’s what one of those tougher ones might look like.
7. At the school cafeteria, 2 boys and 4 girls are forming a lunch line. If the boys must stand in the first and last places in line, how many different lines can be formed?
A. 2
B. 6
C. 48
D. 360
E. 720
Here’s How to Crack It
These restrictions might make this problem seem daunting, but this is where the slot method is really helpful. We have six spots in line to fill, so draw six slots:
It even looks like the line the boys and girls are standing in! Do the restricted spots first. The problem tells us that the two boys must stand in the first and last places in line. This means that either of the boys could stand in first place, and then the other boy will stand in last. This means that we have two options for the first place, but only one for the last.
Now do the same with the unrestricted parts. Any of the four girls could stand in the second spot.
Now, since one of the girls is standing in the second spot, there are only three left to stand in the third spot, and so on, and so on.
Now, as ever, just take the product, to find that the correct answer is (C), 48.
Let’s try one more that tests a few things.
8. Elias has to select one shirt, one pair of pants, and one pair of shoes. If he selects at random from his 8 shirts, 4 pairs of pants, and 3 pairs of shoes, and all his shirts, pants, and shoes are different colors, what is the likelihood that he will select his red shirt, black pants, and brown shoes?
F. 
G. 
H. 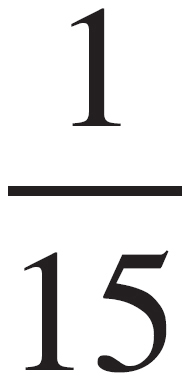
J. 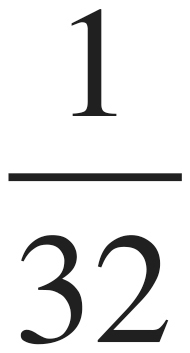
K. 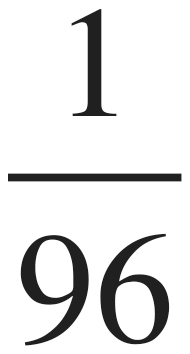
Here’s How to Crack It
Step 1: Know the question. The problem is asking what the probability is that he will select this one group of clothes from all possible combinations of clothes.
Step 2: Let the answers help. The answers offer the important reminder that we’re looking for a probability. We know that it will be only one arrangement out of a reasonably large number of them, so we should at least get rid of (F) and (G).
Step 3: Break the problem into bite-sized pieces. First, we should find the total number of possible combinations. Then, we can deal with the probability.
We have three slots to fill here, and we want to find the product of the three.
Of the 96 possible arrangements, an ensemble of red shirt, black pants, and brown shoes is only one. Therefore, we can go to our  ratio to find
ratio to find 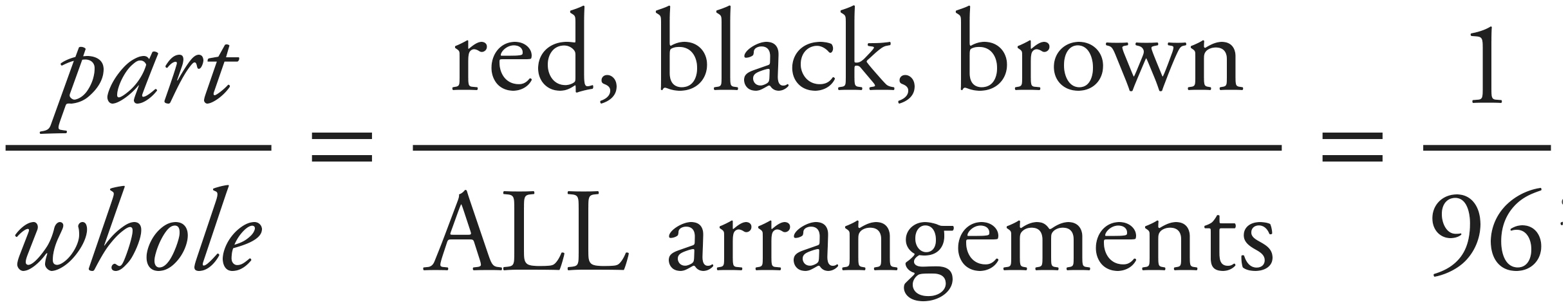 , (K).
, (K).
For the answers to this drill, please go to Chapter 25.
1. The ratio of boys to girls at the Milwood School is 4 to 5. If there are a total of 27 children at the school, how many boys attend the Milwood School?
A. 4
B. 9
C. 12
D. 14
E. 17
2. Linda computed the average of her six biology test scores by mistakenly adding the totals of five scores and dividing by five, giving her an average score of 88. When Linda realized her error, she recalculated and included the sixth test score of 82. What is the average of Linda’s six biology tests?
F. 82
G. 85
H. 86
J. 87
K. 88
3. In the process of milling grain, 3% of the original is lost because of spillage, and another 5% of the original is lost because of mildew. If the mill starts out with 490 tons of grain, how much (in tons) remains to be sold after milling?
A. 425
B. 426
C. 420.5
D. 440
E. 450.8
4. A rectangular box has a base measuring a by a meters and height of b meters. Which of the following represents the surface area of the box?
F. 6ab
G. a2b
H. a2 + 2ab
J. 2a(a + 2b)
K. 2(a2 + b2)
5. In the word HAWKS, how many ways is it possible to rearrange the letters if none repeat and the letter W must go last?
A. 5
B. 15
C. 24
D. 120
E. 650
-
Plugging In works on all kinds of problems, not just Algebra. Always look for opportunities to simplify the math by Plugging In!
-
Percentages and Probabilities are all based on a relationship of PART to WHOLE. Ratios are based on a relationship of PART to PART. Probabilities can be found by taking the part (the number of things that meet some given criteria) divided by the whole (all possibilities, including those that don’t meet the criteria).
-
Percentages can typically be found by multiplying  × 100%.
× 100%.
-
When dealing with percentages, remember to convert Math into English with the handy chart.
|
English
|
Math Equivalent
|
|
percent
|
/100
|
|
of
|
multiplication (×)
|
|
what
|
variable (y, z)
|
|
is, are, were
|
=
|
|
what percent
|
|
-
Ratios are typically a relationship of one part to some other part.
-
On Combination problems
-
Figure out the number of slots you need to fill.
-
Fill in those slots.
-
Find the product.
-
On Average problems, use the average pie.
-
Divide the total by the number of things to find the average.
-
Divide the total by the average to find the number of things.
-
Multiply the number of things by the average to find the total.











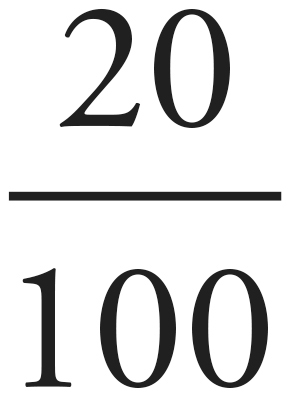 × 100% = 0.2 × 100% = 20%. If you hit 20 of the 100 pitches, you hit 20% of them.
× 100% = 0.2 × 100% = 20%. If you hit 20 of the 100 pitches, you hit 20% of them. =
=  =
= 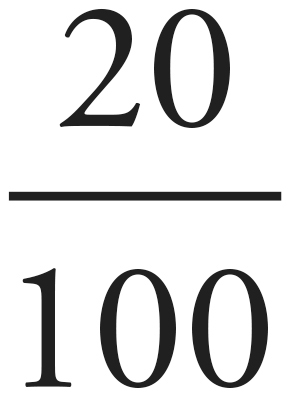 = 0.2. In other words, there’s a 0.2, or
= 0.2. In other words, there’s a 0.2, or  , probability you hit any given pitch during batting practice.
, probability you hit any given pitch during batting practice. , we’ll use
, we’ll use  =
= 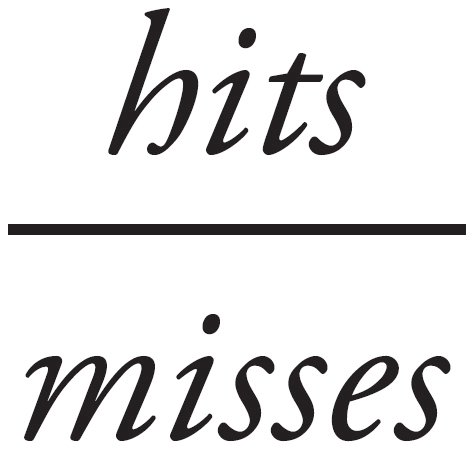 =
= 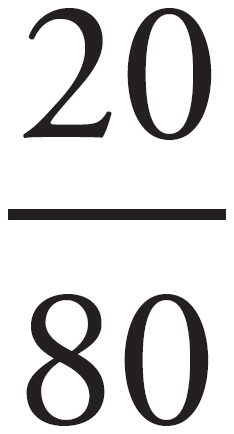 =
=  . The ratio of hits to misses is
. The ratio of hits to misses is  , or 1 to 4, or 1:4.
, or 1 to 4, or 1:4.