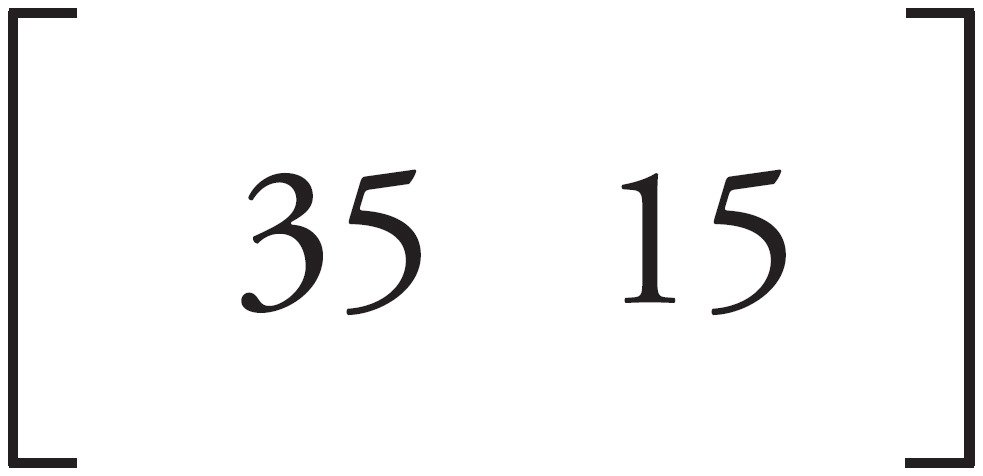You may see logs, vectors, or matrices on your test. It’s good to be familiar with these topics if you’re aiming for a 30+ on the math test, but if any of these concepts make your head spin, don’t sweat it: it’s unlikely that you will see more than one question in each of these topics.
A logarithm is an alternative way to express an exponent.
logb n = x is the same as bx = n
Take a look at this problem.
45. If logx 81 = 4, then x = ?
A. 2
B. 3
C. 9
D. 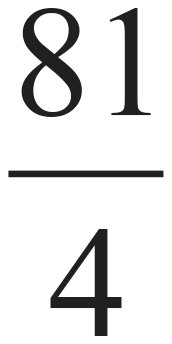
E. 81log4
Here’s How to Crack It
Following the definition of logarithms, logx 81 = 4 can be rewritten as x4 = 81. Take the fourth root of both sides to get  ; which simplifies to x = 3, choice (B).
; which simplifies to x = 3, choice (B).
Since logs are used to express exponents, they follow the same MADSPM rules as exponents:
|
Multiply → Add
|
log xy = log x + log y
|
|
Divide → Subtract
|
 = log x - log y = log x - log y
|
|
Power → Multiply
|
log (xy) = y + log x
|
Try an example problem.
53. Whenever x and y are positive real numbers, which of the following expressions is equal to 4log3 x − log3 5y ?
A. 4log3 (x−5y)
B. 
C. 
D. log3(4x−5y)
E. 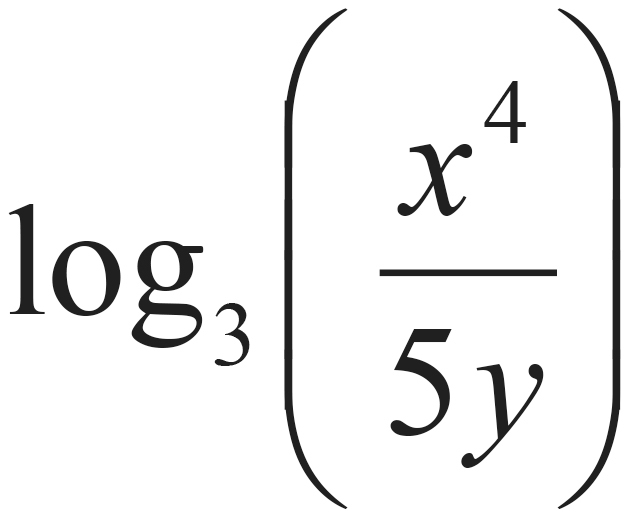
Here’s How to Crack It
Use Bite-Sized Pieces. Since all of the logs in the expression and answers have the same base (3), you can use the MADSPM rules. Using the Power/Multiply rule, 4log3 x = log3 x4. The whole expression can therefore be written: log3 x4 − log3 5y. Now, use the Divide/Subtract rule: log3 x4 − log3 5y = 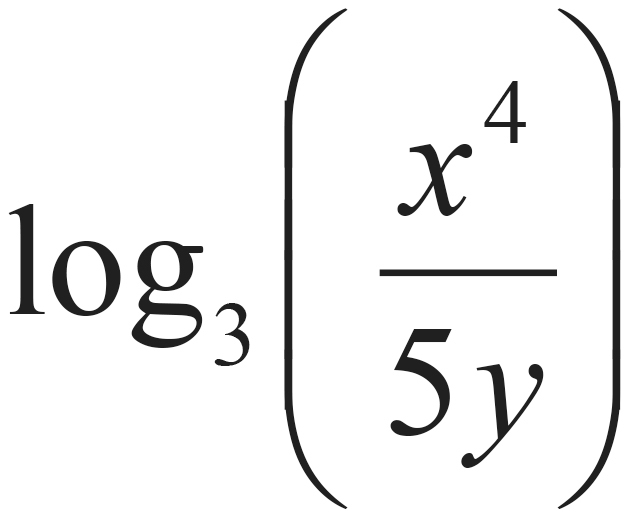 , choice (E).
, choice (E).
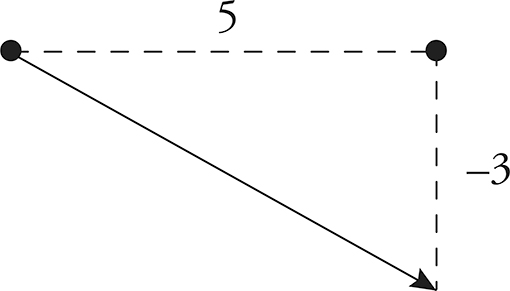
You may also come across a vector question on your test. Vectors are used to notate changes in the x- and y-values on a coordinate plane.
The vector v above can be notated in either of the following manners:
Component Form:
v = <x, y>
Vector v has a component form of <5, −3> because it moves 5 units right and 3 units down. Note that the sign indicates the direction of the change: positive values signal shifts to the right and upward, while negative values denote changes to the left and downward.
To add two vectors in component form, add the x to x and the y to y:
<5, −3> + <c, d> = < 5 + c, −3 + d>
To multiply a vector by a constant, multiply both the x and y values by the constant:
a<5, −3> = <5a, −3a>
Unit Vector Notation:
i = <1, 0> j = <0, 1>
In unit vector notation, vectors are expressed as addition or subtraction of the unit vectors i and j.
Vector v above has the unit vector notation v = 5i − 3j.
You can use the addition and multiplication rules to see how v = 5i − 3j and <5, −3> represent the same vector.
v = 5i − 3j = 5<1, 0> − 3<0, 1> = <5, 0> + <0, −3> = <5, −3>
Vectors in unit vector forms follow the same basic rules as component forms:
To add two vectors, add the i to the i and the j to the j:
(5i − 3j) + (ci + dj) = (5 + c)i + (−3 + d)j
To multiply a vector by a constant, multiply both the i and j values by the constant:
av = a(5i − 3j) = 5ai − 3aj
Let’s try a problem:
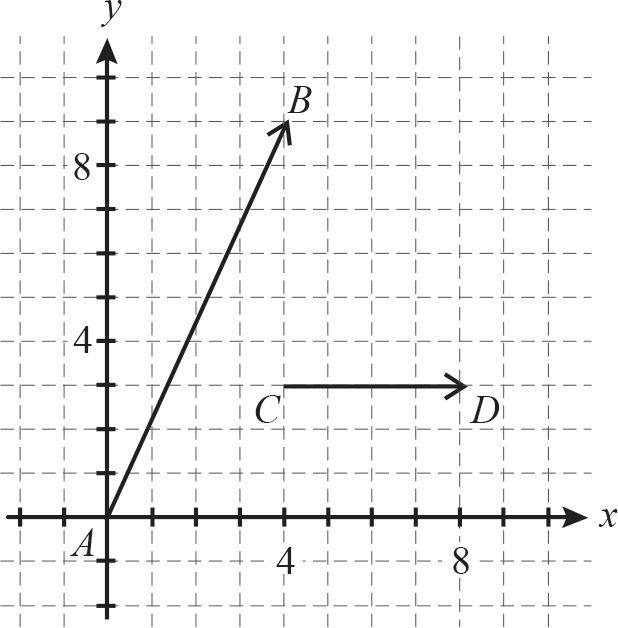
45. Vectors  and
and  are shown in the standard xy-plane below. What is the component form of vector
are shown in the standard xy-plane below. What is the component form of vector  +
+  ?
?
A. <0, 4>
B. <4, 3>
C. <4, 9>
D. <8, 9>
E. <8, 12>
Here’s How to Crack It
The component form of a vector describes the vector in terms of the changes in the x and y values. Vector  starts at (0, 0) and ends at (4, 9), so it increases the x value by 4 and the y value by 9. Therefore, the component form of vector
starts at (0, 0) and ends at (4, 9), so it increases the x value by 4 and the y value by 9. Therefore, the component form of vector  is <4, 9>. Vector
is <4, 9>. Vector  starts at (4, 3) and ends at (8, 3), so the component form is <8 − 4, 3 − 3> = <4, 0>. When adding or subtracting vectors in component form, add or subtract the x values and the y values.
starts at (4, 3) and ends at (8, 3), so the component form is <8 − 4, 3 − 3> = <4, 0>. When adding or subtracting vectors in component form, add or subtract the x values and the y values.  +
+  = <4 + 4, 9 + 0> = <8, 9>, which is (D).
= <4 + 4, 9 + 0> = <8, 9>, which is (D).
An m × n matrix is an array of numbers organized in m rows and n columns.
Matrices may sound scary, but knowing a few basic rules will help you tackle many of the concepts with confidence.
To multiply a matrix by a constant, simply multiply every number by that constant:
To add two matrices with the same dimensions, add the corresponding elements:
The determinant of a 2 × 2 matrix  = ad − bc.
= ad − bc.
Let’s try a problem.
43. If the determinant of the matrix below is 3, n = ?
A. 5
B. 3
C. 3
D. 5
E. 15
Here’s How to Crack It
The determinant of this matrix is 3(6) − [(−5)n] = 18 + 5n. The problem states that the determinant is 3, so 18 + 5n = 3. Subtract 18 from both sides to get 5n = −15; n = −3, which is (B).
Multiplying two matrices is more complicated than adding them. Let your calculator do the hard work when possible, but some questions will require you to understand the concepts. Brush up on your skills if you’re familiar with matrices, but if you’ve never worked with matrices before, then your best bet on difficult multiplication questions is to use your LOTD and keep moving.
To find the product, multiply the elements in each row of the first matrix by the elements in each column of the second and then add the products.
Here’s an example:
It’s a little easier to remember this process when you consider that matrices are used to represent linear equations. Consider the system of linear equations below:
2x + 3y = 10
6x − 5y = 13
This system can be represented by the following matrix equation:
Notice how solving the matrix equation using the matrix multiplication rule gives you  , which yields the two original equations 2x + 3y = 10 and 6x − 5y = 13!
, which yields the two original equations 2x + 3y = 10 and 6x − 5y = 13!
Try this example:
47. The Wittenberg Boating Club sponsors a 2-day sailing excursion. 35 members and 15 nonmembers attend both days of the excursion. For the first day, members are charged $25 and nonmembers are charged $35. For the second day, members are charged $15 and nonmembers are charged $25. Which of the following product matrices represents the total charges each day made by the 35 members and 15 nonmembers who attended both days of the excursion?
A. 
B. 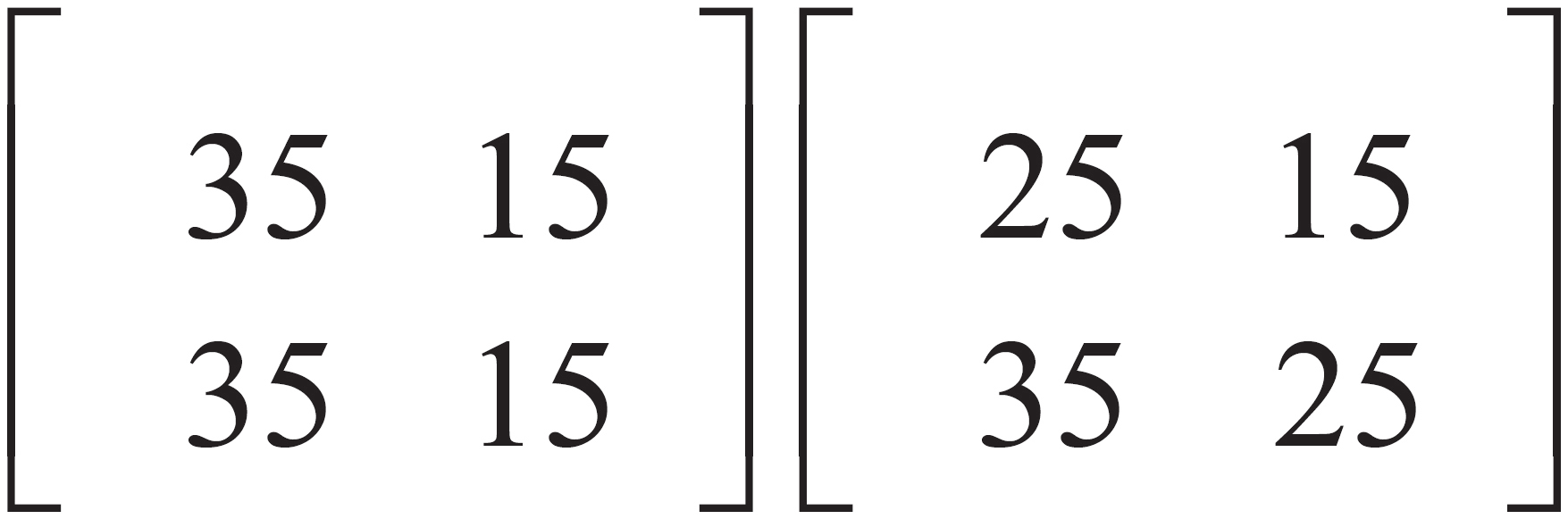
C. 
D. 
E. 
Here’s How to Crack It
The product matrix should multiply the number of members by the prices charged for members and the number of nonmembers by the prices charged to nonmembers, giving a total for each day. Because there should be a total for each day, there should be only two numbers in the resulting product matrix. Choices (A) and (B) multiply a 2 × 2 by a 2 × 2. The product matrix will have the same number of rows as the first matrix (2), and the same number of columns as the second matrix (2), resulting in a 2 × 2 matrix. These matrices will have four numbers, not two, so eliminate (A) and (B). Use POE on the remaining choices. For (C), the row  would first be multiplied by the first column
would first be multiplied by the first column  , resulting in 15 × 25 + 35 × 35. This should represent the total charges for the first day, but this multiplies the number of nonmembers (15) by the price that the members paid (25) and the number of members (35) by the price the nonmembers paid (35). This is incorrect, so eliminate (C). Choice (D) multiplies the row
, resulting in 15 × 25 + 35 × 35. This should represent the total charges for the first day, but this multiplies the number of nonmembers (15) by the price that the members paid (25) and the number of members (35) by the price the nonmembers paid (35). This is incorrect, so eliminate (C). Choice (D) multiplies the row 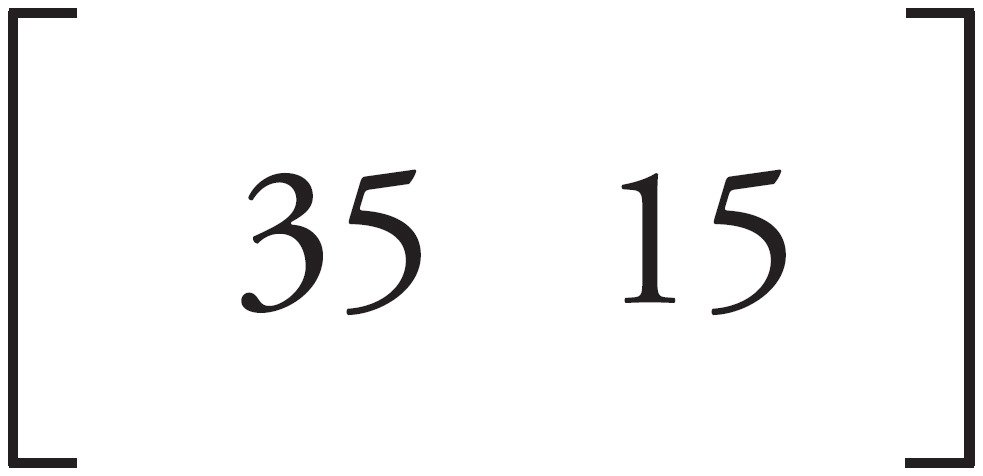 by the column
by the column  . The number of members (35) is multiplied by a price members paid the first day (25), but the number of nonmembers (15) should be multiplied by 35 not 15. This is incorrect; eliminate (D). The answer is (E).
. The number of members (35) is multiplied by a price members paid the first day (25), but the number of nonmembers (15) should be multiplied by 35 not 15. This is incorrect; eliminate (D). The answer is (E).
For the answers to this drill, please go to Chapter 25.
1. If log3 x = 5 , then x = ?
A. 
B. 
C. 15
D. 125
E. 243
2. The component forms of vectors u and v are given by u = <−3, 2> and v = <7, 5>. Given that 4u + (−2v) + w = 0, what is the component form of w ?
F. <−26, −2>
G. <−10, −3>
H. <−4, −7>
J. <10, 3>
K. <26, 2>
3. What value of a satisfies the matrix equation below?

A. 2
B. 4
C. 6
D. 7
E. 8
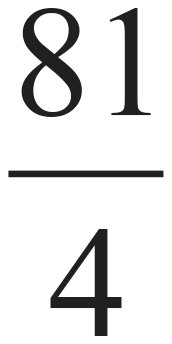
 ; which simplifies to x = 3, choice (B).
; which simplifies to x = 3, choice (B).


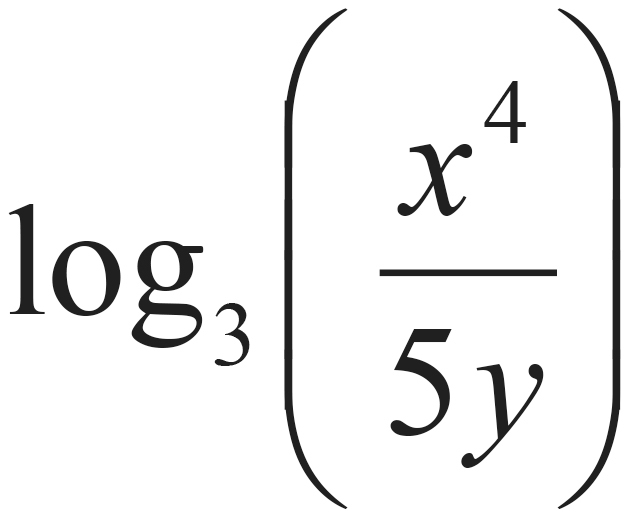
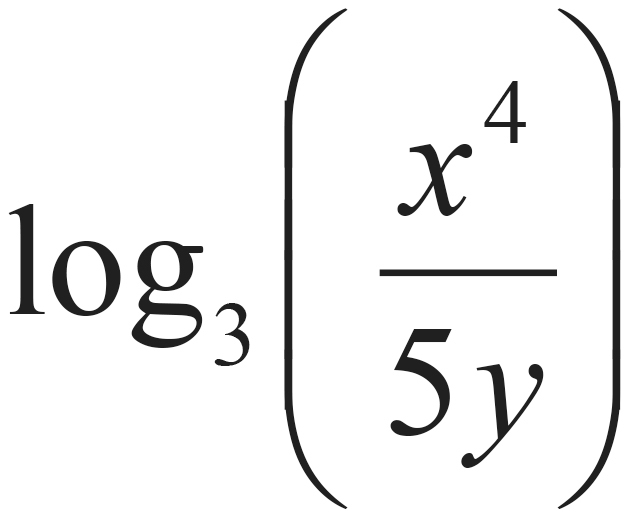 , choice (E).
, choice (E).