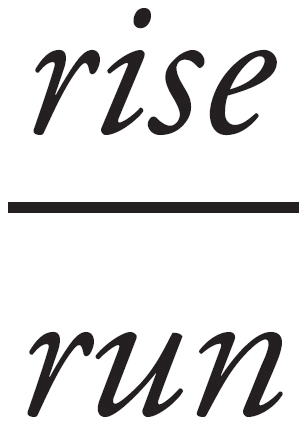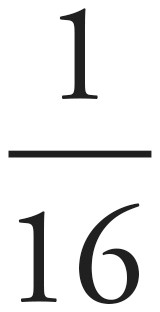Chapter 21

Scientific Reasoning Skills

You don’t need to know science facts for the ACT. For the most part, the Science test is an open-book test, with the passages offering the content you need to answer nearly all the questions. According to ACT, you do need scientific reasoning skills. But all this really means is that you need some common sense. Science may seem intimidating, but it’s based on a lot more common sense than you may think.

YOU KNOW MORE THAN YOU THINK

It’s easy to feel very intimidated by the content and even the figures on the Science test. But all of science is built on common sense. The key to building good scientific reasoning skills is to realize you already have those skills. You use common sense every day to figure things out, to solve problems, to make conclusions. A scientist does the same. When you solve a problem, you think critically, and that’s the basis of scientific reasoning.

How to Solve a Problem

Let’s try an experiment. Say you put on a wool sweater and go out to dinner one night. At the restaurant you order some delectable shrimp for dinner and then a beautiful bowl of strawberries for dessert.

The next morning, you wake up covered in red, itchy hives. What caused them? Do you jump to the conclusion it was the sweater? What about the shrimp? A lot of people have allergies to shellfish. But so, too, do a lot of people have allergies to strawberries. How are you supposed to know which one caused your hives? How do you know any of these options are the only possible culprits?

You don’t. That’s the first rule of scientific reasoning: Make no assumptions. You can’t assume it was the sweater, the shrimp, or the strawberries. But you have to prove it was one and only one of these, if any. So how do you set about finding out which one?

Assumption = Guess

An assumption is nothing more than a guess, and a lazy one at that, if you are willing to believe the riddle has been solved. A guess doesn’t cut it in the scientific world: only proof does.

You design an experiment. You first need to narrow the list of suspects down to the sweater, shrimp, and strawberries. Begin with a baseline. You need to see what happens on a day with none of the possible causes in play to compare to the days with them. Wear a cotton T-shirt and eat cauliflower and cantaloupe. Do you still have hives? Then the three suspects have all been vindicated. But if your hives have cleared up, you’ve confirmed your first hypothesis that it was indeed the sweater, the shrimp, or the strawberries.

Hypothesis

A hypothesis is a theory. An assumption is a guess with no proof. A hypothesis is more advanced than that. It’s a theory that tries to explain what happened, but it requires proof.

Now you have to figure out which one of the three caused your hives. We need a day with one, and one only, of the possibilities, or variables, in play. That’s the second rule of scientific reasoning: Change one variable at a time. On one day wear the sweater, but skip the shrimp and strawberries. On another lose the sweater, and eat the shrimp but not the strawberries. On yet another replace the shrimp with the strawberries. On each day check for hives. The itchy red bumps depend on whatever independent variable is causing them.

Independent and Dependent Variables

The independent variable affects or creates the dependent variable. Does x create or affect y? Some examples of independent variables include time, temperature, and depth. Dependent variables are the events possibly created or affected by an independent variable, and they can be whatever the scientist is studying. Some examples of dependent variables include volume, solubility, and pressure.

That’s all well and good. But what about everything else in your life? Notice we said you couldn’t wear the sweater on the days you ate the shrimp and strawberries. But other than the sweater, you have to wear the exact same clothes on the day you eat shrimp and on the day you eat strawberries. It’s not just what you wear. Everything else in your life has to be exactly the same. If on the day you wore the sweater, you worked out at the gym, but on the day you ate shrimp, you lay on your sofa all day watching television, how much would you know? Not much. Certainly not much of anything with proof, and proof is what it’s all about in science. The third rule of scientific reasoning is that you have to keep all the other variables in the experiment the same as you vary one and only one independent variable. In the hives experiment, this means that in order to conclusively prove the cause, you have to keep everything else the same on each day that you change one and only one independent variable. Do the same things. Wear the same clothes (except the sweater). Eat the same things (except the shrimp and strawberries).

And that’s it. If you follow these three rules, you’ll know what causes your hives.

The Three Rules of Scientific Reasoning

  1. Make no assumptions. You need a standard of comparison to measure against your results. How does your dependent variable react without the presence of any of your independent variables?

  2. Change one variable at a time. Vary each independent variable to see its effect on your dependent variable.

  3. Keep all other variables the same. Your other independent variables and everything else have to be the same as you vary one and only one independent variable.

Trends

In our first example, we looked at a dependent variable, hives, that were present only when an independent variable was present. You’ve undoubtedly faced other situations in which different amounts of a variable seem to have an effect on another variable. The more you study, the better your grades. The more pints of ice cream you eat, the more pounds you gain.

Let’s look at another situation. You sleep only 5 hours a night, staying up late and getting up early to study, but you’re consistently scoring in the high 70s on your daily math quizzes no matter how many hours you study. Suppose you had a hypothesis that if you slept more, your scores would improve. How would you design an experiment to test this? You already have a baseline of 5 hours and consistent scores in the high 70s. So beginning with the first night, you sleep longer, and then see how you score the next day.

The next night, you sleep even longer, and check your quiz score the next day. Can you do anything else differently? No, you have to keep all the other variables in your life the same. Each day you eat the same things and study the same number of hours. You even track quiz scores in the same unit to eliminate any possibility that there is any other reason why your quiz scores improve.

To be organized, you record all your data in a simple table.

Table 1

Hours of sleep

Quiz scores

5

78

6

83

7

88

8

93

As the number of hours of sleep increases, your quiz score increases. In this experiment, the number of hours of sleep is the independent variable, and the quiz score is the dependent variable. You’ve established that your quiz score is directly proportional to the number of hours you sleep.

Direct Proportion

As x increases, y increases. As x decreases, y decreases.

Let’s look at another experiment. Suppose your hypothesis this time is that the more cups of coffee you drink, the fewer hours you sleep. How would you design the experiment? Same rules as always. First, you need a baseline. You need to get all the caffeine out of your system and cut your consumption down to 0 cups each day. You establish a consistent routine of the same diet, exercise, studying, sports practice, and so on. Then, without changing any of those variables, you begin drinking coffee again—same size cup each day—increasing the number of cups and measuring the number of hours you sleep the following night.

Once again, you record your findings in a table.

Table 2

Cups of coffee

Hours of sleep

0

8

1

7

2

6

3

5

As the cups of coffee increase, the hours of sleep decrease. This time, the number of hours of sleep is the dependent variable, and the number of cups of coffee is the independent variable. You’ve established that the amount you sleep is inversely proportional to the amount of coffee you drink.

Inverse Proportion

As x increases, y decreases. As x decreases, y increases.

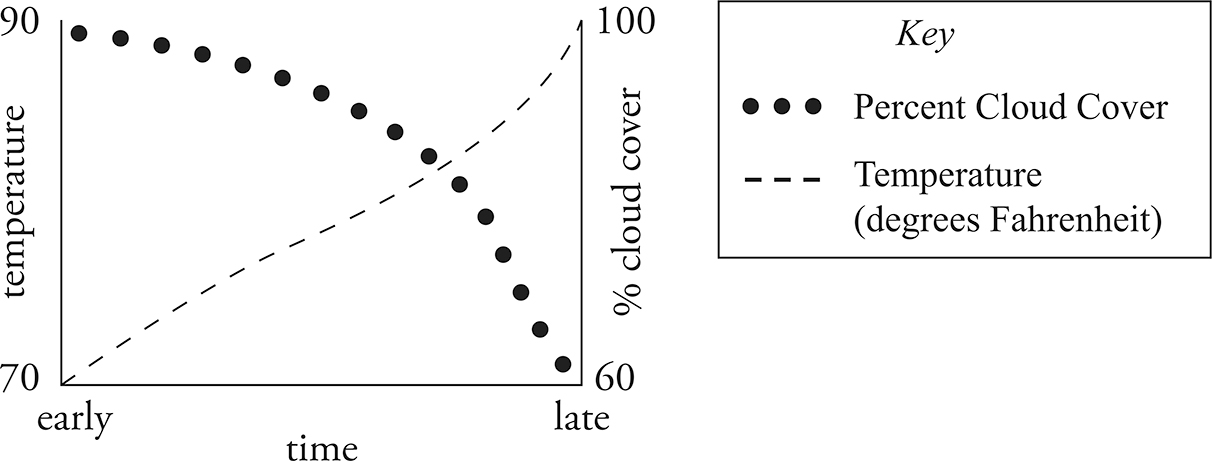
Many passages on the Science test feature passages whose main point is either a direct or inverse trend of the variables. In Chapter 20, we outlined characteristics of Now passages, such as, small tables and graphs with easy-to-spot consistent trends. When you look at the two tables above, the trend is pretty obvious from just a quick glance. You’ve already cracked the main point, and you will find all the questions that much easier to tackle as a result.

Graphs

Tables and graphs both show the trends of variables. Graphs are more visual, making the trends easier to spot.

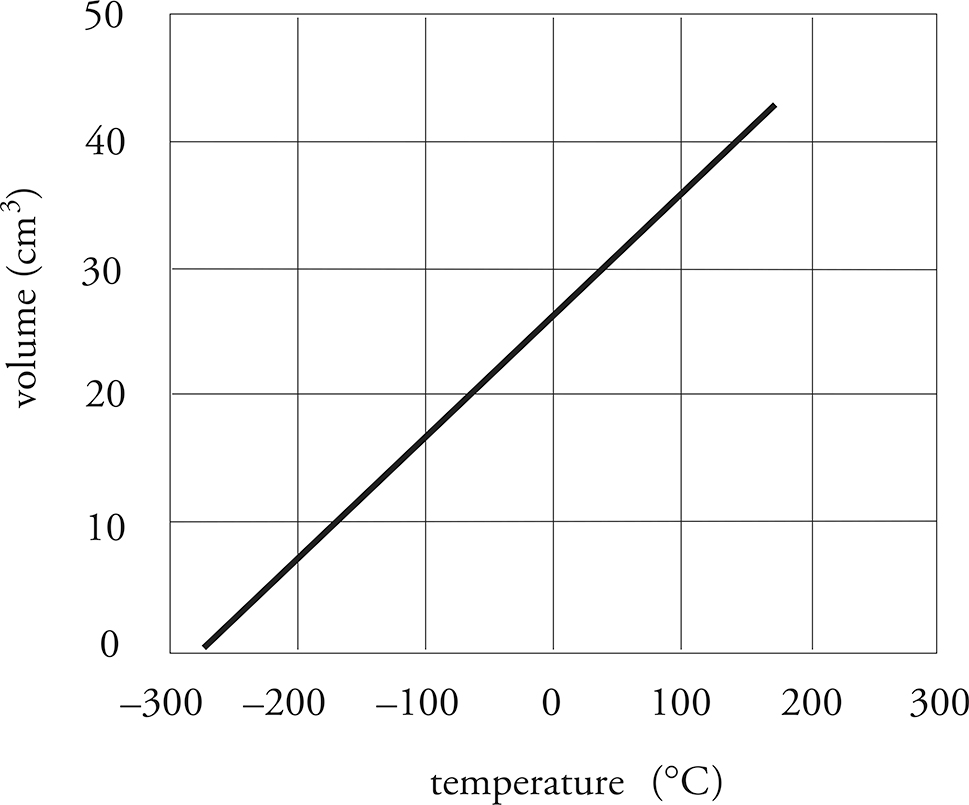
If you graphed your data from Table 1, what would it look like?

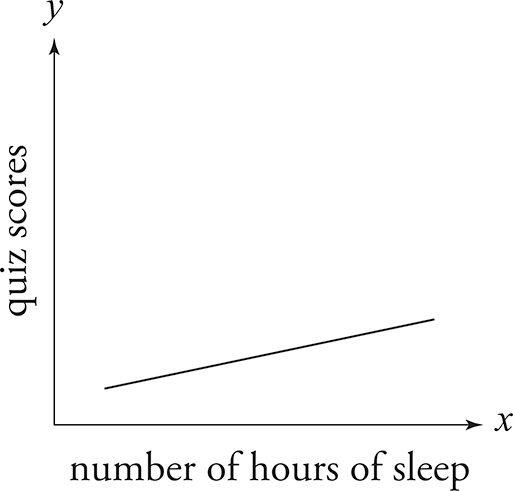
Remember that in math, the horizontal axis is always x: It’s the independent variable. The vertical axis is always y: It’s the dependent variable. Science follows the same rules. This graph shows you that as x increases, y increases. They have a direct relationship.

Slope =

Let’s stick with using math to understand the graphs on the Science test better. Think about slope. It’s the change in y over the change in x. In this graph, the slope is positive. Direct relationships have positive slopes.

Let’s graph Table 2.

This graph shows you that as x increases, y decreases. They have an inverse relationship, and the slope is negative. Inverse relationships have negative slopes.

TRENDS ON THE SCIENCE TEST

The key to cracking the Science test is to look for trends and patterns. Figures with consistent trends point to a Now passage because the figure has provided the main point of the passage—the relationship between the variables.

In the next chapter, we’ll teach you a basic approach to cracking each passage, including passages that don’t feature small tables and graphs with consistent trends. But we hope that this chapter has convinced you to look for passages featuring figures with consistent trends to do Now. You’ll find even the hardest questions are easier to tackle when the figure tells you everything you need to know.

Look at each of the following figures. What are the relationships between the variables?

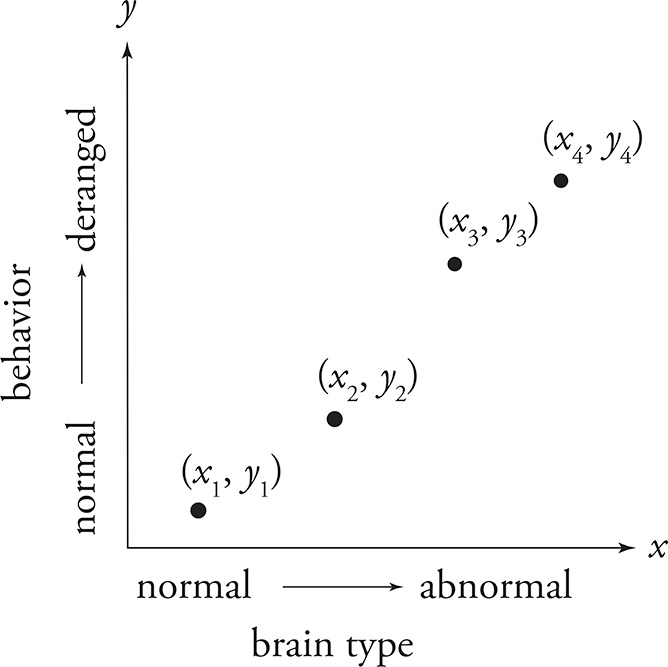
Dr. Frankenstein’s Experiment

As the positive slope of the ordered pairs shows, it’s a direct, linear relationship. The more abnormal the brain, the more deranged the behavior.

Try another.

This, too, is a direct, linear relationship. As temperature increases, volume increases.

What about the next one?

When the wind speed is 40 km/hr, what is the rate of sand movement? It’s 0.3. When the wind speed is 50 km/hr, the rate of sand movement increases to 0.6, double the last reading even though the wind speed increased by only 10 km/hr. The relationship is direct, but the curve shows you it’s an exponential relationship, not a linear one.

Curves = Exponential Change

When the dependent variable changes by a different amount every time the independent variable changes, the result will be a curved line.

Try the next one.

Does time actually affect the size of a soda can? Of course not. As a result, we get a flat line.

Try one more.

As the number of expired half-lives increases, the amount of thorium remaining decreases, so the two have an inverse relationship.

Do you need to know what “expired half-lives” and “thorium” are? No, you don’t need to (but it’s always helpful when you’re familiar with the content). To answer the questions for this passage, everything you need to know comes from the relationships between the variables. The main point of the passage is just a summary of these relationships.

Tables

When we began this chapter, we showed you tables before switching to graphs. Everything we’ve discussed about graphs applies to tables. A table with consistent trends is just as helpful as a graph with consistent trends. The only difference is that tables are not as visual as graphs, so it’s up to you to make them visual.

Look at the table below.

Number of half-lives expired for radioactive thorium

Amount of thorium (gm) remaining

0

1

1

2

3

4

This is the same information we saw in a graph. What direction is the number of half-lives headed? It’s headed up. Draw an arrow to reflect the trend. What direction is the amount of thorium headed? It’s headed down. Draw an arrow to reflect the trend. Your table should now look like this:

You’ve just gotten a preview of the next chapter. Marking the trends in a figure is the first step in the basic approach to cracking Science passages.

Inconsistent Trends and No Relationships

Wouldn’t it be great if you saw only tables and graphs with consistent trends on the ACT? Yes, it would, but there will be uglier figures as well. Now that you know how powerful consistent trends are, you can actually use that knowledge even when there is no consistency. The absence of consistency tells its own story.

As temperature increases, what does pH do? It barely increases at first, then makes a sharp jump before an equally sharp fall to a point that is lower than where it began. You may have immediately identified this as a bell curve. Is a bell curve consistent?

A bell curve is certainly not as consistent as a straight line or even a curve that moves in a positive or negative direction. There is some consistency, however. It increases, then decreases. The problem is that we can’t make a prediction of what it will do next. That’s the real beauty of consistent lines and curves: We can predict what will happen off the figure. But with a bell curve, we can’t determine whether it will repeat its trend or if it will steadily decrease.

What about the next graph? What story does it tell?

There is no relationship at all between Aedes aegypti and sarcoidosis. The incidence of sarcoidosis is independent of the Aedes aegypti, not dependent. And unlike the relationship in a flat line, the incidence of sarcoidosis is not constant. Instead, it fluctuates wildly.

That’s a good deal of information from a confusing figure with two strange variables. But would you want to do the passage with this figure Now or Later? Definitely Later.

Multiple Variables

In many Experiments passages, you’ll see multiple tables and graphs. Take a look at the following tables (Tables 3 and 4).

Table 3

Length (m)

Resistance (Ω)

0.9

7.5

1.8

15.0

3.6

30.0

Table 3

Table 4

Cross-sectional area (mm2)

Resistance (Ω)

0.8

35.0

1.6

18.0

3.2

7.5

Table 4

First, mark the trends within each figure. In Table 3, as length increases, resistance increases. Length is the independent variable, resistance is the dependent variable, and the two have a direct relationship. In Table 4, as cross-sectional area increases, resistance decreases, and the two have an inverse relationship. What’s the relationship between the figures? Look at the variable they have in common: resistance.

In Experiments passages—as well as in scientific studies in real life—it’s common to test different independent variables to measure their effect on the same dependent variable. But recall our second and third rules of scientific reasoning skills:

When length is varied, can cross-sectional area vary at the same time? No, it has to stay the same, that is, constant. And when cross-sectional area is varied, length has to stay constant.

On the Science test, you are likely to see a question that tests your ability to spot the constants.

1. Based on the results shown in Table 3 and Table 4, the cross-sectional area used in the first experiment (resulting in Table 3), was most likely:

A. 0.8 mm2.

B. 1.6 mm2.

C. 3.2 mm2.

D. 4.8 mm2.

Here’s How to Crack It

Find the link between the two tables by looking at the variable they have in common, resistance. Look for a value of resistance that is the same in both tables. In Table 3, resistance is 7.5 Ω when length is 0.9 m. In Table 4, resistance is 7.5 Ω when cross-sectional area is 3.2 mm2. Thus, we know that as length was varied, cross-sectional area was held constant at 3.2 mm2, and as cross-sectional area was varied, length was held constant at 0.9 m. The correct answer is (C).

Graphs can also have multiple variables. Take a look at the following graph.

When there are multiple variables on a graph, you always need to be careful to look at the correct line and the correct axis. As time increases, temperature increases. As time increases, cloud cover decreases. Does this data mean that temperature and cloud cover have a direct relationship? Not necessarily. What’s the variable they have in common? Time.

Try another question.

2. According to the figure above, what was the temperature, in degrees Fahrenheit, when cloud cover was at its highest?

F. 100°

G. 90°

H. 60°

J. 70°

Here’s How to Crack It

Find the link between the two axes by looking at the variable they have in common, time. Be sure to look at the correct curve on the correct axis. Cloud cover is the bubbled line, and when it’s at its highest, the time on the x-axis is early. When time is early, look at the dashed line for the temperature. When it’s early, the temperature is 70°.

The correct answer is (J).

In the next lesson, we’ll teach you how to use your scientific reasoning skills on ACT Science passages, which will feature plenty of tables and graphs with various trends and relationships.

Summary