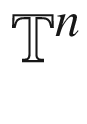Volume 289

Graduate Texts in Mathematics

Series Editor

Ravi Vakil

Stanford University, USA

Advisory Editors

Alejandro Adem

University of British Columbia, Vancouver, BC, Canada

David Eisenbud

University of California, Berkeley & MSRI, Berkeley, CA, USA

Brian C. Hall

University of Notre Dame, Notre Dame, IN, USA

Patricia Hersh

University of Oregon, Eugene, OR, USA

Jeffrey C. Lagarias

University of Michigan, Ann Arbor, MI, USA

Eugenia Malinnikova

Stanford University, Stanford, CA, USA

Ken Ono

Emory University, Atlanta, GA, USA

Jeremy Quastel

University of Toronto, Toronto, ON, Canada

Barry Simon

California Institute of Technology, Pasadena, CA, USA

Steven H. Weintraub

Lehigh University, Bethlehem, PA, USA

Melanie Matchett Wood

Harvard University, Cambridge, MA, USA

Graduate Texts in Mathematics Series Editors: Stanford University bridge the gap between passive study and creative understanding, offering graduate-level introductions to advanced topics in mathematics. The volumes are carefully written as teaching aids and highlight characteristic features of the theory. Although these books are frequently used as textbooks in graduate courses, they are also suitable for individual study. bridge the gap between passive study and creative understanding, offering graduate-level introductions to advanced topics in mathematics. The volumes are carefully written as teaching aids and highlight characteristic features of the theory. Although these books are frequently used as textbooks in graduate courses, they are also suitable for individual study. Ravi Vakil,

More information about this series at Advisory Board: University of British Columbia University of California, Berkeley MSRI University of Notre Dame University of Oregon http://www.springer.com/series/136 Alejandro Adem, David Eisenbud, & Brian C. Hall, Patricia Hersh,

J.F. Jardine,University of Western Ontario Jeffrey C. Lagarias,University of Michigan

Eugenia Malinnikova,Stanford University

Ken Ono,University of Virginia Jeremy Quastel,University of Toronto Barry Simon,California Institute of Technology

Steven H. Weintraub,Lehigh University

Melanie Matchett Wood,Harvard University

Jane Hawkins

Ergodic Dynamics

From Basic Theory to Applications

1st ed. 2021

../images/491076_1_En_BookFrontmatter_Figa_HTML.png

Jane Hawkins

Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, NC, USA

ISSN 0072-5285e-ISSN 2197-5612

Graduate Texts in Mathematics

ISBN 978-3-030-59241-7e-ISBN 978-3-030-59242-4

https://doi.org/10.1007/978-3-030-59242-4

Mathematics Subject Classiﬁcation (2010): 37A0537B1037F1037A3537A4037B15

This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.

The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.

The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This Springer imprint is published by the registered company Springer Nature Switzerland AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

To Michael and Diane

Preface

The word ergodic is one of many scientific portmanteau words that were assembled from Greek words, in this case by mathematical physicists. They produced a new label for a type of dynamical behavior exhibiting some “uniform randomness.” Words for work (ergon) and path (odos) were combined to give ergodic; but, why was that meaningful? To make sense of work-path, we consider a system of many moving particles, such as a fluid, with the property we can understand the entire system reasonably well by measuring and averaging the work done along just one randomly chosen orbit path. Then, there is a certain intrinsic randomness exhibited by the dynamical system, since we do not know in advance which initial point of the more than 10²⁷ possibilities to follow; we call this system ergodic. Another way to think of an ergodic dynamical system is to imagine that any randomly chosen point has an orbit that passes through a neighborhood of every possible state of the system, spending the right proportion of its time there through its recurring visits. Therefore, following the path of one point tells you about the entire system. Unfortunately, not all dynamical systems have this indecomposability to them, and not every point in an ergodic system will unlock the behavior of the whole system. It is in understanding whys or why nots, the basic examples, and stronger related properties that we get into the beautiful mathematics of the subject of ergodic theory.

The term ergodic was coined by Boltzmann in the late 1860s in the context of the statistical mechanics of gas particles; it is relevant that he was wrong, or at least overly hopeful in his original conjecture that every classical system of interest was ergodic. The term was subsequently adopted by both mathematicians and physicists, its meaning bifurcated and mutated over the decades, and it currently means slightly different things to mathematicians, applied mathematicians, and physicists. Vocabulary that comes into existence in this contrived way frequently leaves most readers out in the cold. One goal of this text is to show that the mystery surrounding ergodic theory is unwarranted. The subject could just as easily be called dynamical systems, except that studying the subject using only topology and calculus does not capture the essence of the probabilistic randomness involved in an ergodic system. We study topological dynamical systems in this book too, as the interplay between the topological and statistical properties in many physical and natural examples is what lends so much beauty to the subject. In fact, from the start, we give all of our dynamical systems both topological and measurable structure to avoid deciding which tool kit we can use; we hope to show the reader how to use both interchangeably.

The book grew from the notes used in ergodic theory and dynamical systems courses taught at the University of North Carolina at Chapel Hill at least a dozen times over the past decades. The topics contain both the common core of all those courses and diverse paths taken into subject areas from these courses. A similar course was also taught at Duke University by the author, where some of the applications were added and then remained in some subsequent courses.

This book is intended for an introductory course on the main ideas and examples in ergodic theory and their connections to dynamical systems, using some classical and current applications. A solid grounding in measure theory, topology, and complex analysis will make the book readily accessible. However, a brief review of these essentials can be found in the appendices if some material is missing from the reader’s background. Appendix A provides a detailed synopsis of Lebesgue measure on 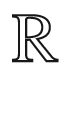$\mathbb R$ and then extrapolates to measures on other spaces by relegating detailed proofs to the texts mentioned in the references. In Appendix B, we focus on a brief review of Lebesgue integration and Hilbert space theory, while Appendix C provides the basic connections to probability theory.

The text is written so that the first several sections of each chapter invite the reader to delve into the material. It can be used as a text for a one-semester course in dynamical systems for graduate students or upper-level undergraduates. Students looking for a senior honors thesis or a master’s topic might try some of the problems mentioned in the text or dig deeper into some of the applications mentioned. Our focus is on presenting many of the basic examples in their simplest and often their original form. Many of the earliest purely mathematical examples of ergodic transformations were constructed by John von Neumann and have woven their way into the fundamental structure of computers, information theory, and cellular automata. Some of the examples are hard to find in the literature today and deserve a new look. There are also recent results and applications presented along the way.

Another intended audience for this book are those with some mathematical background who want to learn the underpinnings of ergodic theory but do not have the time or inclination to work through some of the well-written yet thick texts on the subject. There are exercises given at the end of every chapter, including the appendices.

One way to teach a one-semester course from this text is to cover one chapter per week, assigning problems from the end of each chapter. This works well when the students have adequate background in measure theory and functional analysis. On the other hand, many of the chapters, after the preliminary material is presented in Chapters 1–4, can be read as standalone chapters or in pairs with related titles. Some versions of the course that have been taught in one semester include the following: Chapters 1–6, 8, and 11; Chapters 1, 2, and 4–11; Chapters 1–5 and 8–12; and Chapters 1, 2, and 4–9. At the end of many chapters, there is a section consisting of an application of the math presented in the chapter to this field. While a few of these applications are classical, many are relatively new fields of exploration and provide the basis for student projects or further research.

There are three optional appendices containing background material on measure theory, integration, and Hilbert spaces, and a brief appendix on connections to probability theory. They also include exercises.

Acknowledgments

There are many people who made contributions to the mathematical content, organization, and readability of this book. The graduate students in my courses over thirty years were among the earliest readers of my course notes and made numerous valuable suggestions, especially Joanna Furno. Notes from courses taught at the University of North Carolina at Chapel Hill, Duke, and CalTech, as well as summer courses taught at George Washington University in the Summer Program for Women in Math provide a basis for a large part of this book. Any analysis questions I had were answered by Michael Taylor, and many useful comments about applications were provided by Jim Franklin. I am particularly grateful for the many helpful comments provided by anonymous reviewers, which greatly improved the book.

Jane Hawkins

Chapel Hill, NC, USA

August 2020