When writing a report, investigating a crime scene, or just making observations, it will be important for you to be able to calculate (even if you’re just estimating) areas and perimeters of rooms, open areas such as parks, and other types of spaces. Here’s a quick review of how to calculate the area and perimeter of spaces.
Mathematically speaking, the area of a space is the two-dimensional surface occupied by that space. You will likely encounter areas when reporting square footages of a room or building. Area is a fairly easy formula to remember, particularly since most rooms, buildings, parking lots, etc., are approximate squares or rectangles. Triangles and circles get a bit trickier. But how often do you encounter a triangular room or a circular parking lot? For these reasons, let's focus solely on squares and rectangles.
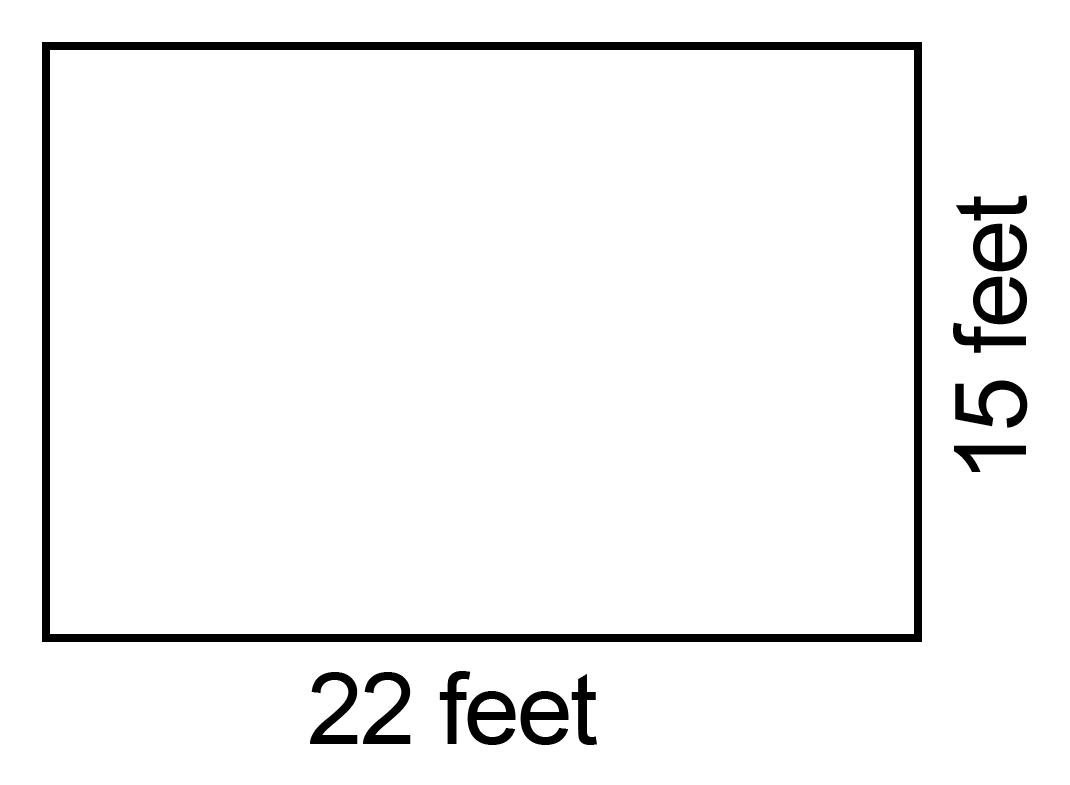
In the example below, the room’s dimensions are 15 feet by 22 feet. Assuming that the parallel walls are the same size, the area of this room is calculated by multiplying the length (l) times the width (w) or
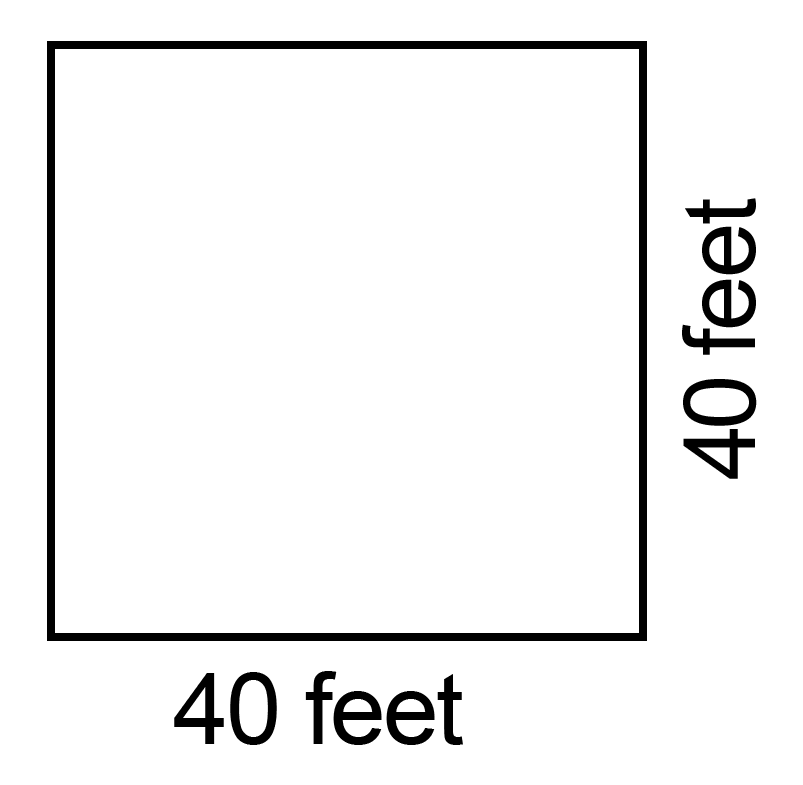
Calculating the area of a square space is even simpler. Since a square has four equal sides, you simply square the length of one side, often written as 
. So, for the square playground below, the calculation for its area would be
.
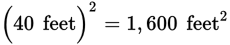Perimeter is a term you’ve likely heard on TV cop shows. “Secure the perimeter of the park with 20 officers.” You know what a perimeter is—the outer edge of a space—but do you remember how to calculate it? Let’s use the room and the playground examples from above.
A perimeter of a shape is the sum of all its sides. So, in this case, the perimeter of this room = 22 feet + 15 feet + 22 feet + 15 feet, simplified as 2 x (22 feet + 15 feet) = 74 feet.
Likewise, the perimeter of the playground above is 40 feet + 40 feet + 40 feet + 40 feet, simplified as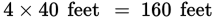 
.