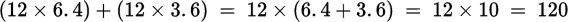, where A is the numerator and B is the denominatorSome police exams may test basic mathematics to ensure you are comfortable working with numbers. This chapter reviews some of the building blocks of math. If you are comfortable with the concepts presented in this chapter, facing everyday problems that require a basic knowledge of addition, subtraction, multiplication, and division will be a smooth process.
Most of you have encountered these rules and practices in school, though it may have been a while since you’ve reviewed the exact terms and concepts. For some of you, this chapter will just be a basic brush up of skills you are comfortable with. Others may have to study this chapter carefully to relearn the basics. Like grammar and spelling, no matter what your actual exam tests, reviewing this chapter and completing the practice questions can only enhance your confidence going into Test Day.
Familiarize yourself with these key terms and concepts, so you don't come across any surprises when you take your exam.
Integers: all whole numbers, including zero, and their negative counterparts
Examples: −900, −3, 0, 1, 54
Addends: any number added to another in an equation
Example: 1 + 2 = 3
In this equation, 1 and 2 are the addends.
Fractions: a number that is written in the form , where A is the numerator and B is the denominator
Example:
An improper fraction has a numerator with a greater absolute value than that of the denominator.
Example:
A mixed number consists of a whole number and a fraction.
Example:
An improper fraction can be converted to a mixed number and vice versa.
Example:
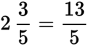
Positive/negative: Numbers greater than 0 are positive numbers; numbers less than 0 are negative numbers. 0 is neither positive nor negative.
Examples:
Positive:
Negative:
Even/odd: An even number is an integer that is a multiple of 2; an odd number is an integer that is not a multiple of 2. Fractions and mixed numbers are neither even nor odd.
Examples:
Even numbers: −8, –2, 0, 12, 188
Odd numbers: −17, −1, 3, 9, 457
Factor: a positive integer that divides evenly into a given number
Example:
The complete list of factors of 12: 1, 2, 3, 4, 6, 12
Prime number: an integer greater than 1 that has no factors other than 1 and itself; 2 is the only even prime number
Examples: 2, 3, 5, 7, 11, 59, 83
Consecutive numbers: numbers that follow one after another, in order, without skipping any
In a series of consecutive numbers, the differences between any consecutive numbers are equal.
Examples:
Consecutive integers: 3, 4, 5, 6
Consecutive even integers: 2, 4, 6, 8, 10
Consecutive multiples of −9: −9, −18, −27, −36
Multiple: A multiple of a number is the product of that number and an integer.
Example:
Some multiples of 12: 0, 12, 24, 60
No matter what line of work you are in, you will always encounter formulas in everyday life. When traveling abroad, you may need to convert a temperature from degrees Celsius to degrees Fahrenheit to better understand it. You may need to calculate the perimeter or area of a room in order to accurately describe it. Formulas exist for all kinds of situations.
When simplifying a mathematical expression after you have plugged values into your formula, you do not simply work from left to right, as you do when you read a book. Just as there are rules for driving an automobile, there are rules for order when performing arithmetic operations. There is a predetermined order of operations used to evaluate expressions. Perhaps you remember the mnemonic for remembering the order of operations: PEMDAS. Some of you may have used the memory tool “Please Excuse My Dear Aunt Sally” to recall the correct order.
The order of operations is:
P: Parentheses (grouping symbols)
E: Exponents
MD: Multiply and divide from left to right
AS: Add and subtract from left to right
The P in PEMDAS stands for parentheses, or grouping symbols. Grouping symbols include parentheses, brackets, the absolute value symbol, and a fraction bar. So, to simplify 
, treat the fraction bar as a grouping symbol and first evaluate the top (the numerator) and then the bottom (the denominator). Then you will divide for the final step.
To simplify the numerator, first simplify your exponent: 102 = 100. Second, multiply 4 times 2 to get 8. The top is now 18 + 100 – 8. Evaluate from left to right: 118 – 8 = 110. To simplify the denominator, first divide 27 by 3 to get 9. Then subtract: 20 – 9 = 11. Finally, divide 110 by 11 to get 10.
When plugging numbers into formulas, a working knowledge of the order of operations is essential. For example, to convert a temperature from degrees Fahrenheit to degrees Celsius, you use the formula 
, where F is the degrees in Fahrenheit and C is the degrees in Celsius. If you have a temperature of 77 degrees Fahrenheit, and you want to know the equivalent degrees in Celsius, substitute in 77 for F in the formula: 
. First, subtract 32 from 77, because parentheses are evaluated first: 
. Now, multiply 
by 45 
to get 25 degrees Celsius.
There are common properties of numbers that are frequently used to make adding and multiplying easier. You most likely use these properties without even realizing it when you do mental arithmetic or when you add a column of numbers. These properties give you the license to change the order of operations in certain situations. In addition to making addition and multiplication of number terms easier to calculate, these three properties are frequently used in solving algebraic equations.
The commutative property of addition states that changing the order of the addends in a sum does not change the sum: a + b = b + a, where a and b are any real numbers.
For example:
The order of operations would dictate that 12.3 would first be added to 6.9. But the addition is easier if you first add 12.3 to 7.7 because the sum will equal a whole number. The commutative property gives you this freedom.
Similar to the commutative property of addition, the commutative property of multiplication states that changing the order of the factors in a product does not change the product: 
, where a and b are any real numbers.
For example:
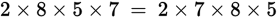
If you scan a group of factors to find subproducts to equal 10, 100, or 1,000, it is easiest to multiply these factors first. The commutative property allows you to make these changes to the order of operations.
The associative property also pertains to either the addends in a sum or the factors in a product. The associative property of addition or multiplication states that changing the grouping (parentheses or brackets) of addends in a sum or the grouping of factors in a product does not change the resulting sum or product:
, where a, b, and c are any real numbers.
, where a, b, and c are any real numbers.
For example, to add 9.8 + (10.2 + 6.1) + 4.9, the order of operations would call for you to evaluate inside the parentheses first and then to add from left to right. But the sum of 9.8 and 10.2 is 20, and the sum of 6.1 and 4.9 is 11. The associative property allows you to change the grouping by adding: (9.8 + 10.2) + (6.1 + 4.9), to get 20 + 11 = 31. Notice in the example that the order of the addends did not change, just the grouping.
You can also use a combination of the properties. For example, to simplify the expression 2.1 + 8.07 + 7.9 + 24.93, scan the addends and recognize that (2.1 + 7.9) and (8.07 + 24.93) will produce whole numbers. Use the commutative property to get 2.1 + 7.9 + 8.07 + 24.93. Then use the associative property to get (2.1 + 7.9) + (8.07 + 24.93). Now the addition is easy to finish: 10 + 33 = 43.
The distributive property involves two operations: addition and multiplication or subtraction and multiplication.
The distributive property of multiplication over addition or subtraction states that multiplication distributes over addition and subtraction:
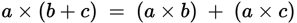, where a, b, and c are real numbers.
, where a, b, and c are real numbers.
For example, if you want to multiply 16 by 8, you may not know the multiples of 16. However, you do know the multiples of 10 and 6. The distributive property allows you to rewrite 
as 
, or simply 8(10 + 6). Because multiplication distributes over addition, this problem becomes 
, which can be evaluated as 80 + 48 = 128. Likewise,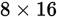 
could be written as 
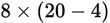or:
You can also use the distributive property in reverse. For example, if you were instructed to simplify 
, order of operations would have you evaluate parentheses first, which involves decimal multiplication. If you notice that both terms are multiplied by 12, use the distributive property to factor out the 12:
