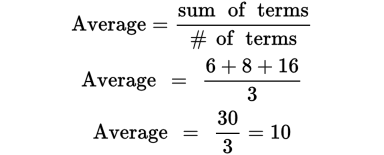
Working quickly and efficiently is essential to maximizing your score on the math questions you will face on your police exam. To accomplish this, use the following method:
Read the entire question carefully before you start solving the problem. If you don’t read the question carefully, you may make a careless mistake or overlook the simplest approach to answering the question.
Before you choose your approach, make sure you know what you’re solving for. In other words, what does the correct answer choice represent? This is an important step to keep you from falling for tempting wrong answer choices. For example, if you are given an equation with two variables, x and y, identify whether you are solving for x, for y, or for something else. This step is important because your exam may give you wrong answer choices that represent the “right answer to the wrong question.” That is, if you are asked to solve for x, one wrong answer choice might represent the value of y.
Once you understand what the question is asking you to solve, it’s time to look for the most strategic approach. Use your analysis from Steps 1 and 2 to find the most efficient route to the correct answer. This step might involve performing calculations (that is, “doing the math”), or it might be the case that applying a strategy would get you to the correct answer more quickly. This chapter will discuss these strategic approaches.
Reread the question as you select your answer. Make sure you are answering the question asked. If you notice that you missed something earlier, rework the problem and change your answer if necessary.
Here’s an example of the steps in action:
One bag contains 6 pieces of candy, another bag contains 8 pieces, and a third bag contains 16 pieces. What is the average number of pieces of candy in a single bag?
Step 1. Analyze the information given:
The question tells you the number of pieces of candy in three bags.
Step 2. Identify what you are being asked for:
You are being asked to calculate the average number of candies in one bag.
Step 3. Solve strategically:
Use the average formula:
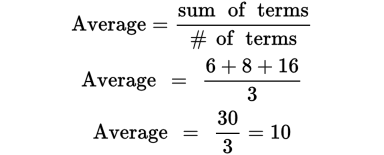
The average is 10, or Choice (C).
Step 4. Confirm your answer:
Don’t rework the math from scratch; rather, ask yourself whether the answer makes sense given what you were asked for. Does 10 seem like a likely average given the numbers 6, 8, and 16?
Yes. Since the average of a set of numbers has a value that’s between the smallest and largest numbers in the set, 10 makes sense as an answer.
Several methods are extremely useful when you don’t know—or don’t have time to use—the textbook approach to solving the question. In addition, performing all the calculations called for in the question can often be more time-consuming than using a strategic approach and can increase the potential for mistakes.
Let's now explore four of those strategic methods:
Sometimes it’s easiest to work backward from the answer choices. Since many math questions are word problems with numbers in the answer choices, you can often use this to your advantage by backsolving, or working backward from the available answer choices. After all, the test gives you the correct answer—it’s just mixed in with the wrong answer choices. If you try an answer choice in the question and it fits with the information given, then you’ve got the right answer.
Here’s how it works. When the answer choices are numbers, you can expect them to be arranged from small to large (or occasionally from large to small). Start by trying either Choice (B) or (C). If that number works when you plug it into the problem, you’ve found the correct answer. If it doesn’t work, you can usually figure out whether to try a larger or smaller answer choice next. Even better, if you deduce that you need a smaller (or larger) number, and only one such smaller (or larger) number appears among the answer choices, that choice must be correct. You do not have to try that answer choice: simply select it and move on to the next question.
By backsolving strategically this way, you won’t have to try out more than two answer choices before you zero in on the correct answer. To see an example of backsolving, check out the following problem and explanation.
An appliance store reduced the price of a refrigerator by 20 percent and then raised the price by 10 percent from the lower price. What was the original price of the refrigerator, if the final price was $70.40?
Step 1. Analyze the information given:
The price of a refrigerator is reduced 20 percent and then that reduced price is raised 10 percent. The final price is $70.40.
Step 2. Identify what you are being asked for:
The correct answer represents the original price, before the changes.
Step 3. Solve strategically:
To answer this question using algebra would be complex and time-consuming and would introduce many opportunities for errors. Instead, since all the answer choices are numbers, backsolve.
Start by trying out Choice (B), $70:
$70 reduced by 20 percent: $70 − $14 = $56
$56 raised by 10 percent: $56 + $5.60 = $61.60
That’s lower than the final price of $70.40, so Choice (B) is too low. Now, you can eliminate both answer Choices (B) and (A).
Now try either (C) or (D). (D) is easier for a percent problem.
Reduce $100 by 20 percent: $100 − $20 = $80
Raise that $80 by 10 percent: $80 + $8 = $88
That final price is far too high, so (C) must be the correct answer.
Step 4. Confirm your answer:
The answer of $80 is the only one that is neither too large nor too small to yield the final price of $70.40 specified in the question. So, you're done!
In backsolving, when you start with Choice (B) or (C) and that answer doesn’t work, you’ll usually know which direction to go. For example, if the answer choices are listed smallest to largest and Choice (B) is too large when you plug it in, you will know that Choice (A) is the correct answer. If, on the other hand, Choice (B) is too small, you will know that the answer is Choice (C) or (D).
Another strategy that comes in handy on many math questions is picking numbers. Just because the question contains numbers in the answer choices, that doesn’t mean that you can always backsolve. There may be numbers in the answer choices, but sometimes you won’t have enough information in the question to easily match up an answer choice to a specific value in the question stem.
For example, a problem might present an equation with many variables, or it might give you information about percentages of some unknown quantity and ask you for another percent. If the test maker hasn’t provided you with a quantity that would be really helpful to have in order to solve the problem, you may be able to simply pick a value to assign to that unknown. The other case in which you can pick numbers is when there are variables in the answer choices.
When you are picking numbers, be sure that the numbers you select are permissible (following the rules of the problem) and manageable (easy to work with). In general, it’s a good idea to avoid picking −1, 0, or 1 because they have unique number properties that can skew your results.
Here’s a great example showing how picking numbers can make an abstract problem concrete.
When n is divided by 14, the remainder is 9. What is the remainder when n is divided by 7?
Step 1. Analyze the information given:
An unknown number, n, is 9 larger than a multiple of 14.
Step 2. Identify what you are being asked for:
The correct answer represents the remainder when n is divided by 7.
Step 3. Solve strategically:
To make this abstract question concrete, pick a number for n that leaves a remainder of 9 when divided by 14. The most manageable number to pick that is also permissible in the problem is n = 23 (because 14 + 9 = 23).
Now try out your number: 23 ÷ 7 = 3 with a remainder of 2.
Therefore, Choice (B) is the correct answer.
Step 4. Confirm your answer:
Briefly look back over the math to check that you are solving for the correct value. Confirm, and you're all set!
When there are variables in the problem and in the answer choices, you can pick numbers for those variables. Evaluate the expression in the question stem using your chosen numbers, and then evaluate each answer choice using the same numbers. Your goal is to find the answer that yields the same numerical result as the one you calculated using your chosen numbers. When you use this method, you must evaluate all of the answer choices. If more than one yields the same numerical result, choose a different set of numbers to evaluate only the remaining choices that gave matching solutions with the first set of numbers that you chose.
To solve problems containing variables in the question stem and answer choices using picking numbers, start by picking permissible and manageable numbers for the variables. Answer the question using the numbers you’ve picked. This answer is your target number. Then substitute the numbers you picked for the variables into the answer choices. You are looking for the answer choice that gives you the target number.
Take a look at this example:
For all r, s, t, and u, what does r(t + u) − s(t + u) equal?
Step 1. Analyze the information given:
You are given an algebraic expression and asked to find an equivalent expression.
Step 2. Identify what you are being asked for:
The correct answer simplifies the expression r(t + u) − s(t + u).
Step 3. Solve strategically:
Since you are given no values for any of the four variables, you can pick numbers for each of them.
Some good numbers to pick here are r = 5, s = 4, t = 3, and u = 2. You can, however, use any permissible and manageable numbers you wish.
Replacing the variables in the expressions with the numbers picked yields the following:
5(3 + 2) − 4(3 + 2) = 25 − 20 = 5
Then replace the variables in each answer choice to see which choice gives the target number of 5:
(A) (r + s)(t + u)(5 + 4)(3 + 2) = (9)(5) = 45 Incorrect
(B) (r − s)(t − u)(5 − 4)(3 − 2) = (1)(1) = 1 Incorrect
(C) (r + s)(t − u)(5 + 4)(3 − 2) = (9)(1) = 9 Incorrect
(D) (r − s)(t + u )(5 − 4)(3 + 2) = (1)(5) = 5 Correct!
Step 4. Confirm your answer:
In this example, only Choice (D) works. If more than one choice gives a correct answer, you need to pick another set of numbers and try only those answer choices again.
Sometimes, you can determine the characteristics of a correct answer without doing a lot of calculations. Study the example below.
After eating 25 percent of the pretzels, Sonya had 42 left. How many pretzels did Sonya have originally?
Step 1. Analyze the information given:
Original # of pretzels − 25 percent of pretzels = 42
Step 2. Identify what you are being asked for:
The correct answer represents the original number of pretzels, before Sonya ate any.
Step 3. Solve strategically:
Because 25 percent is the same as one-quarter, the correct answer must be divisible by 4 with no remainder. If the number of pretzels Sonia started with was not divisible by 4, and she then ate  of the pretzels, she’d be left with fractions of pretzels left over. Of the answer choices, only Choice (C) 56 is evenly divisible by 4, so it has to be the correct answer.
of the pretzels, she’d be left with fractions of pretzels left over. Of the answer choices, only Choice (C) 56 is evenly divisible by 4, so it has to be the correct answer.
Step 4. Confirm your answer:
One-quarter of 56 is 14, and 56 − 14 = 42, the number of pretzels Sonya had left.
If at all possible, try to avoid doing extensive calculations; rather, see if you can eliminate some answer choices based on logic.
There is no rule that says you have to use just one approach to get the correct answer. Study the example below.
Shoshanna bought a new cell phone, cell phone case, and wall charger. The cell phone cost $149.99, the case cost $19.99, and the wall charger cost $29.99. If tax on each of these items was 9.5 percent, which of the following is closest to the total amount Shoshanna spent?
Step 1. Analyze the information given:
You are told the prices of three items that Shoshanna purchased, plus a sales tax rate.
Step 2. Identify what you are being asked for:
You are asked to find the answer that is closest to the total amount Shoshanna paid for her purchases.
Step 3. Solve strategically:
Because you are asked for the closest amount, you do not have to use an exact calculation to find the correct answer. Estimation will work well. Round the prices for each item before tax to the nearest dollar.
Shoshanna spent $150 + $20 + $30 = $200 before tax. You can eliminate Choices (A) and (B) because they are too small. Now round the tax rate to 10 percent. Because 10 percent of $200 is $20, Shoshanna spent about $200 + $20 = $220 in total. Choice (D) is correct.
Step 4. Confirm your answer:
Check that you did the arithmetic correctly and that the answer makes sense. All the other answer choices are too low to be close to what she spent.
Sometimes, you’ll find that you have to make a guess, but don’t guess at random. Narrow down the answer choices to increase your odds of guessing the correct one. First, eliminate answer choices you know are wrong. Next, avoid answer choices that don’t make logical sense. Finally, choose one of the remaining answer choices.