CAPITOLO 9
L’eredità di Fibonacci
in lapidi, pergamene e conigli
Dopo diversi secoli di oblio, Leonardo è oggi onorato a Pisa con un’imponente lapide e una bella statua di marmo bianco. Tuttavia, il suo nome (o, meglio, il suo soprannome ottocentesco) viene ricordato soprattutto in virtù di uno dei quesiti inclusi nel Liber abbaci. Anche se il problema in sé era soltanto un rompicapo ricreativo senza troppe pretese, la sequenza di numeri che costituisce la sua soluzione – i numeri di Fibonacci – rappresenta una parte importante dell’eredità culturale di Leonardo.
Verso la fine del capitolo 12 del Liber abbaci, in mezzo a una serie di problemi concernenti la suddivisione di cibo e di denaro, Leonardo infilò un bizzarro enigma sulla crescita di una popolazione di conigli. Il problema in questione non era farina del suo sacco, ma risaliva perlomeno ai matematici indiani dei primi secoli dopo Cristo (gli stessi che avevano sviluppato il sistema numerico descritto dal Liber abbaci); il matematico pisano – al pari dei suoi predecessori indiani – si rendeva però perfettamente conto di come questo rompicapo potesse offrire un eccellente strumento per far pratica nell’uso del nuovo sistema numerico. Anche se le ultime generazioni di storici della matematica considerano il Liber abbaci come uno dei libri più influenti mai scritti, per la maggior parte della gente comune la fama del suo autore riposa su quest’unico problema. In quello che sarebbe diventato il suo passo più famoso, Leonardo si guadagnò un posto nella cultura popolare del XX secolo attraverso le seguenti parole:
QUANTE COPPIE DI CONIGLI NASCONO IN UN ANNO
DA UNA SINGOLA COPPIA
Un uomo mise una coppia di conigli in un luogo chiuso da pareti; voleva scoprire quante ne sarebbero nate in un anno, assumendo che per natura ogni coppia generi una nuova coppia al mese e che al secondo mese i nuovi nati inizino a loro volta a procreare.1
Leonardo vuole che il lettore assuma che, una volta che una coppia di conigli è diventata fertile, continuerà a generare una nuova coppia ogni mese. Come al solito, Fibonacci spiega la soluzione nel dettaglio, ma il lettore moderno può cogliere al volo il metodo risolutivo dando un’occhiata alla tabella da lui riportata, dove viene indicato il numero di coppie di conigli per ciascun mese:
| Coppie di conigli |
| All’inizio | 1 |
| Al termine del primo mese | 2 |
| Al termine del secondo | 3 |
| Al termine del terzo | 5 |
| Al termine del quarto | 8 |
| Al termine del quinto | 13 |
| Al termine del sesto | 21 |
| Al termine del settimo | 34 |
| Al termine dell’ottavo | 55 |
| Al termine del nono | 89 |
| Al termine del decimo | 144 |
| Al termine dell’undicesimo | 233 |
| Al termine del dodicesimo | 377 |
La regola generale afferma che ogni numero successivo è dato dalla somma dei due precedenti: 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 e così via. Come Leonardo sottolinea al termine della sua soluzione, attraverso questa semplice regola possiamo calcolare la popolazione non solo alla fine di un anno (377), ma dopo un qualunque numero di mesi.
I numeri generati dal processo di addizione descritto da Leonardo per risolvere il problema dei conigli sono oggi noti come i numeri di Fibonacci. Sembra che abbiano fatto la loro prima comparsa nel Chandahshastra (L’arte della prosodia), un trattato sanscrito scritto dal grammatico Pingala fra il 450 e il 200 a.C. La prosodia – lo studio del ritmo, dell’accentazione e dell’intonazione del discorso – aveva grande importanza negli antichi rituali indiani. Nel VI secolo, il matematico indiano Virahanka mostrò l’emergere di questa sequenza nell’analisi di metri con sillabe lunghe e brevi; in seguito, il filosofo giainista Hemachandra (1150 circa) compose un testo su questi rapporti numerici.
I numeri di Fibonacci ricevettero il loro nome dal matematico francese Edouard Lucas negli anni Settanta dell’Ottocento; qualche decennio prima, nel 1838, un suo compatriota, lo storico Guillaume Libri, aveva dato a Leonardo il soprannome di Fibonacci. Gran parte del fascino di questi numeri è dovuto alla sorprendente frequenza con cui li ritroviamo nel mondo naturale.
Per esempio, il numero dei petali dei fiori è un numero di Fibonacci più spesso di quanto ci si potrebbe aspettare stando al semplice caso: l’iris ha 3 petali; la primula, il ranuncolo, la rosa canina, la speronella e la colombina ne hanno 5; il delfinio ne ha 8; l’erba di san Giacomo, il crisantemo campestre e la cineraria 13; l’astro, la rudbeckia e la cicoria 21; le margherite 13, 21 o 34; e le pratoline 55 o 89.
Le infiorescenze dei girasoli e le basi delle pigne mostrano delle spirali che vanno in direzioni opposte: il girasole ne ha 21, 34, 55, 89 o 144 orarie, accoppiate, rispettivamente, a 34, 55, 89, 144 o 233 antiorarie; una pigna presenta 8 spirali orarie e 13 antiorarie. Sono tutti numeri di Fibonacci.
Un terzo esempio emerge nella fillotassi, che studia la disposizione delle foglie sui rami delle piante: salendo lungo il ramo o lo stelo, la posizione delle foglie segue la linea di una spirale. Partiamo da una foglia e indichiamo con p il numero di giri completi della spirale prima di trovare una seconda foglia direttamente sopra la prima; indichiamo quindi con q il numero di foglie che si incontrano procedendo dalla prima fino a quest’ultima (esclusa la prima). Il rapporto p/q è chiamato «la divergenza della pianta». Divergenze comuni sono: ½ (olmo, tiglio, lime e qualche tipo di erba comune), 1/3 (faggio, nocciolo, rovo, carice e qualche tipo d’erba), 2/5 (quercia, ciliegio, melo, agrifoglio, prugno e senecione), 3/8 (pioppo, rosa, pero e salice); 5/13 (mandorlo, salicone e porro). Di nuovo, tutti rapporti fra numeri di Fibonacci.
L’elemento matematico chiave che sta alla base dell’apparente predilezione della natura per i numeri di Fibonacci è la loro stretta connessione a una costante matematica altrettanto famosa nota come la Sezione aurea. Spesso indicata con la lettera greca φ (phi), la Sezione aurea è, come p, un numero irrazionale, ossia un numero la cui espansione decimale prosegue all’infinito senza mai ripetersi secondo uno schema regolare. L’espansione decimale di p inizia con 3,14159, quella di φ con 1,61803.
Il numero φ fece la sua prima comparsa negli Elementi di Euclide (scritti attorno al 350 a.C.), dove venne definito come il rapporto secondo cui dobbiamo dividere una linea perché la linea intera stia alla sua parte più lunga come quest’ultima sta a quella più corta. Euclide lo chiamò «rapporto estremo e medio»; nel XV secolo, il matematico italiano Luca Pacioli gli diede il nome più evocativo di Divina proportione, pubblicando un trattato in tre volumi con questo titolo; nel 1835, poi, in un libro scritto dal matematico Martin Ohm, il numero φ venne battezzato «sezione aurea».
Con due nomi così suggestivi – uno che si richiama al divino, l’altro all’oro –, questo numero è stato l’oggetto di diverse false convinzioni: che sia il rapporto larghezza/altezza che l’occhio umano trova più piacevole, cosa che spinse gli antichi Greci ad adottarlo in gran parte delle loro opere architettoniche, tra cui il Partenone di Atene; che diversi pittori e musicisti l’abbiano usato nelle loro composizioni; che se misurate la distanza dalla sommità della vostra testa al pavimento e la dividete per la distanza dal pavimento del vostro ombelico, otterrete la sezione aurea; e molte altre leggende. Qualche società d’investimento si è addirittura spinta a sostenere di raggiungere risultati migliori delle altre basando le proprie azioni sulla sequenza di Fibonacci. Nessuna di queste affermazioni è in grado di reggere anche solo a un esame sommario.
C’è tuttavia un fenomeno in cui la sezione aurea si presenta per davvero: la crescita delle piante. L’inesorabile predilezione della natura per l’efficienza fa sì che la disposizione dei petali dei fiori, dei loro semi e delle foglie sui rami dipenda dalla sezione aurea, dato che quest’ultima gode di una proprietà matematica che conduce a un’ottimizzazione della struttura.
La connessione fra i numeri di Fibonacci e la sezione aurea venne verificata per la prima volta nel XIX secolo: se ogni numero di Fibonacci viene diviso per quello che lo precede, man mano che avanziamo nella sequenza il risultato ottenuto si avvicina progressivamente alla sezione aurea; nella terminologia matematica, la sezione aurea è il limite a cui tendono quei rapporti. (I primi valori sono: 
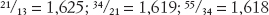 Dato che φ è un numero irrazionale, mentre il numero dei petali, delle spirali o degli stami in una pianta o in un fiore dev’essere un numero intero, la natura «arrotonda» al numero intero più vicino; e, per via della proprietà del limite di cui sopra, quest’ultimo tenderà a essere un numero di Fibonacci.
Dato che φ è un numero irrazionale, mentre il numero dei petali, delle spirali o degli stami in una pianta o in un fiore dev’essere un numero intero, la natura «arrotonda» al numero intero più vicino; e, per via della proprietà del limite di cui sopra, quest’ultimo tenderà a essere un numero di Fibonacci.
Nel 1963, la passione per i numeri di Fibonacci ha portato alla costituzione della Fibonacci Association, che pubblica a cadenza trimestrale la rivista matematica «Fibonacci Quarterly». L’associazione e la sua rivista sono dedicate alle ricerche sui numeri di Fibonacci e sulle sequenze di questo tipo. In genere, non si tratta di una matematica molto profonda; tuttavia, le sequenze di numeri generate in un modo simile a quella di Fibonacci tendono a presentare diverse proprietà matematiche affascinanti.
Nel 1241, il Comune di Pisa decretò il versamento di uno stipendio annuale a Fibonacci per i servigi da lui resi alla città (si tratta, fra l’altro, dell’unico documento che ci permette di affermare che nel 1241 il matematico era ancora vivo). Il testo dell’editto è stato riprodotto su una lapide eretta dalla città in onore del suo grande antenato il 16 giugno 1867; si trova su un muro all’ingresso dell’Archivio di Stato di Pisa, al numero 30 del Lungarno Mediceo (la strada che costeggia la riva nord dell’Arno). Il testo medievale è introdotto da una dichiarazione scritta nel 1865.
L’edificio in questione è già di per sé interessante. Noto in precedenza come Palazzo Toscanelli, apparteneva in origine alla famiglia Lanfranchi ma passò poi ad Alessandro della Gherardesca, che vi effettuò diverse modifiche architettoniche. Nel 1821-1822, in un periodo in cui Pisa era chiamata «il paradiso degli esuli», ospitò Lord Byron e il suo circolo di amici; da lì il poeta sarebbe poi partito per la Grecia, dove avrebbe incontrato la morte.
L’iscrizione, composta in un latino ottocentesco molto formale, può essere tradotta come:
Nell’anno 1865, le autorità e il popolo di Pisa, ignorando le vecchie falsità e seguendo la volontà degli anziani di studiare ciò che era meglio noto e dimostrato su Leonardo Fibonacci, ordinarono agli archivi cittadini di presentare una copia del decreto della stessa eminentissima Repubblica di Pisa, sì che sia data testimonianza imperitura a un così grand’uomo.
[Il decreto del 1241]
In considerazione dell’onore e del profitto portati alla nostra città e ai suoi cittadini dall’insegnamento e dalla diligente obbedienza di maestro Leonardo Bigollo, uomo distinto e sapiente, nei suoi calcoli e conti con l’abbaco svolti per la città e i suoi funzionari, assieme ad altri suoi servigi, con il presente decreto stabiliamo che allo stesso Leonardo, con gratitudine e diletto, e in prerogativa della sua scienza, come ricompensa del lavoro da lui svolto nei suddetti calcoli e conti, riceva dal Comune e dai suoi funzionari e per il Comune una ricompensa o salario annuale di venti lire pisane, più le spese secondo consuetudine; lo stesso Leonardo continuerà da parte sua a prestare al solito modo i suoi servigi al comune pisano e ai suoi ufficiali nel campo dei calcoli.2
Anche qui compare il soprannome «Bigollo», questa volta in un contesto dove di certo non poteva significare «testa di legno».
Oltre a un’incisione, tutto sommato recente, che mostra la testa e le spalle di un giovane, l’unica immagine che abbiamo di Leonardo è una statua eretta a Pisa nel XIX secolo. Sia l’incisione sia la statua sono considerate creazioni artistiche, non basate sulla realtà. (La statua, pur rappresentando un uomo di mezza età, è abbastanza simile all’incisione, cosa che ci induce a supporre che lo scultore, Giovanni Paganucci, possa essersi ispirato a essa nella sua opera.) La statua, in marmo bianco, si trova nel Camposanto (il cimitero monumentale) di piazza dei Miracoli, vicino alla Torre pendente. Il volto di Leonardo è ritratto secondo i lineamenti classici: una faccia con un naso stretto, una mascella ben pronunciata e una fossetta nel mento. È rappresentato in piedi, avvolto da una lunga tunica cadente, con la testa coperta da un cappuccio che gli dà un’aria vagamente clericale; da sotto il cappuccio spuntano due ciocche di capelli ricci. Dal suo piedistallo, Leonardo guarda verso il basso con un’espressione affabile da studioso, tenendo in mano un libro;A l’altra mano è tesa in avanti, come se stesse gesticolando per evidenziare un punto a uno studente. A entrambe le mani mancano delle dita a causa dei danni subiti durante la Seconda guerra mondiale.
Sul piedistallo alla base della statua si legge l’iscrizione:
A
Leonardo Fibonacci
Insigne Matematico
Pisano
del Secolo XII
(La data è un po’ fuorviante: anche se Leonardo era nato attorno al 1170, tutte le sue pubblicazioni matematiche videro infatti la luce nel XIII secolo.)
Sul retro del piedistallo, in basso a destra, compare un’iscrizione più piccola che recita:
G. Paganucci
Firenze 1863
La storia di questa statua è interessante.3 L’iniziativa della sua creazione non venne presa a Pisa ma a Firenze, da due politici appartenenti a famiglie dell’antica aristocrazia toscana: il barone Bettino Ricasoli e il marchese Cosimo Ridolfi. Nel 1859 il granduca di Toscana andò in esilio e l’anno seguente la regione venne annessa al regno dei Savoia, che sarebbe in breve tempo diventato il nuovo Stato italiano. Durante la transizione, la Toscana era retta da un governo provvisorio di cui Ricasoli era il primo ministro e Ridolfi il ministro dell’Istruzione; entrambi ebbero un ruolo attivo nella promozione della cultura e, fra l’altro, fondarono un moderno istituto per gli studi avanzati che sarebbe in seguito diventato l’Università di Firenze. Il 23 settembre 1859, Ricasoli firmò un decreto che stabiliva che la Toscana avrebbe finanziato la creazione di tre statue, rispettivamente per Pisa, Lucca e Siena. Ognuna di esse avrebbe dovuto commemorare un importante personaggio del luogo; quella di Pisa sarebbe stata dedicata a Fibonacci, citato dal decreto come «l’iniziatore degli studi algebrici in Europa». L’opera venne commissionata allo scultore fiorentino Giovanni Paganucci, che la completò nel 1863; fu collocata quindi nel Camposanto, accanto alle statue di molti altri eminenti pisani, e venne inaugurata ufficialmente il 17 giugno.
La statua rimase al Camposanto fino al 1926, quando le autorità fasciste allora al governo di Pisa la rimossero assieme ad altre due statue per metterle in tre piazze della città, dove potessero servire come testimonianza di alcune delle grandi personalità a cui Pisa aveva dato i natali. Tutte e tre le statue erano di individui indicati come «Pisano»: oltre a Leonardo, c’era una famosa coppia (padre e figlio) di scultori e architetti, Nicola e Giovanni Pisano. All’iscrizione sul piedistallo di ciascuna statua fu aggiunta una frase che recitava:
Dall’oblio alla gloria per volontà fascista.
Le autorità fasciste posero Leonardo in una posizione prominente, di fronte alle Logge dei Banchi, un’elegante piazza a sud del Ponte di Mezzo, che attraversa l’Arno nel centro della città. Per far posto al nuovo arrivato venne rimosso il busto di un politico minore dell’Ottocento, Felice Cavallotti; al contempo, la piazza fu ribattezzata «piazza XX Settembre» (in commemorazione della data in cui, nel 1870, la città di Roma, fino ad allora sotto il governo dei papi, era stata conquistata dal neonato Stato italiano, proclamato nel 1861).
Verso la fine della Seconda guerra mondiale, le truppe americane e tedesche combatterono una violenta battaglia – protrattasi per un mese – dalle rive opposte dell’Arno, durante la quale il ponte finì distrutto, la piazza fu gravemente danneggiata e diversi edifici circostanti rimasero in rovina; in qualche modo, però, la statua di Leonardo riuscì miracolosamente a sopravvivere, riportando solo qualche leggero danno alle mani. Una splendida fotografia scattata poco dopo lo scontro mostra Leonardo che si erge quasi incolume in mezzo a un mare di macerie.
Al termine della guerra, la statua venne rimossa per consentire la ricostruzione del ponte e della piazza. Dato che anche il Camposanto era parzialmente in rovina e doveva essere risistemato, non fu però possibile riportarla al suo posto originale; venne invece piazzata dentro un magazzino, dove restò dimenticata per due decenni.
Nel 1966, la statua fu infine tirata fuori dal deposito e messa in mostra nel Giardino Scotto,4 un piccolo parco pubblico sulle rive dell’Arno, adiacente a un tratto di strada chiamato Lungarno Leonardo Fibonacci. Purtroppo, il giardino in questione è un luogo molto amato non solo dalle persone, ma anche dagli uccelli, e nel corso degli anni la statua, oltre a perdere il suo colore a causa delle intemperie, finì anche per ricoprirsi di escrementi. La statua nel parco, scura e imbrattata, fu immortalata in una fotografia di Frank Johnson che si può trovare su molti siti web. Attorno al 1990, venne portata via e restaurata, per poi essere infine ricollocata al Camposanto.
Una parte dell’eredità di Leonardo molto più significativa della sequenza di Fibonacci, della lapide commemorativa o della statua di marmo è data dal corpus di quattordici manoscritti medievali del Liber abbaci che sono giunti fino a noi; dato che gli originali delle edizioni del 1202 e del 1228 sono andati perduti, queste quattordici copie superstiti dell’edizione del 1228 sono le più vicine al suo capolavoro originale.
Sette di esse sono meri frammenti, costituiti da un numero molto limitato (da uno e mezzo a tre) dei quindici capitoli del libro, e altre quattro sono un po’ frammentate; di queste, sei si trovano a Firenze, tre a Parigi, una a Milano e una a Napoli.B Le rimanenti tre sono complete o quasi e si trovano tutte in Italia. Si ritiene che una di esse (custodita nella Biblioteca Nazionale Centrale di Firenze)5 risalga alla fine del XIII secolo o, al più tardi, all’inizio del XIV; il manoscritto risulta completo, il che probabilmente spiega perché Baldassarre Boncompagni l’abbia usato come base per la sua prima edizione a stampa del Liber abbaci (nel 1857), anche se potrebbe non essere il più antico. Un altro, da cui manca il decimo capitolo, è custodito nella Biblioteca vaticana a Roma,6 e si ritiene che risalga al tardo XIII secolo. Il terzo si trova nella Biblioteca comunale di Siena7 ed è generalmente datato al XIII secolo, forse al 1275; secondo alcuni studiosi, potrebbe essere il più vecchio, anche se altri hanno ipotizzato che potrebbe essere stato composto ben un secolo dopo.
Il fatto che nessuno degli antichi manoscritti si trovi a Pisa potrebbe sembrare curioso, ma c’è una spiegazione plausibile. In un’epoca in cui ogni copia di un testo richiedeva una faticosa preparazione a mano, non c’erano incentivi a tenerne una in una città che disponeva già di un manoscritto, gli originali di Leonardo; pertanto, le copie prodotte erano presumibilmente destinate a essere usate altrove. Le città di Roma, Firenze e Siena sono quindi i luoghi più probabili dove trovare delle copie.
La mia ricerca su Leonardo mi ha portato diverse volte in Italia e, in due occasioni, ho avuto modo di esaminare i manoscritti di Siena e Firenze. (La Biblioteca vaticana è rimasta chiusa per restauri per qualche anno, con la conseguente impossibilità di avere accesso ai manoscritti rari.) Conoscevo già i contenuti del libro grazie alla traduzione inglese di Sigler, ma volevo provare la sensazione di tenere in mano il manoscritto di un’opera da cui ero attratto da anni, un manoscritto che, pur non essendo stato composto dallo stesso Leonardo, risalisse comunque alla sua epoca (forse lo scriba aveva iniziato a copiarlo quando l’autore era ancora in vita) e fosse pertanto simile all’originale.
La Biblioteca comunale di Siena si trova al numero 5 di via della Sapienza, a pochi minuti di cammino da piazza del Campo, il centro della città. Il manoscritto è grande e pesante: misura più di 20,5 centimetri di larghezza per 30 di altezza e 5 di spessore, senza contare la massiccia copertina, dal colore marrone sbiadito, scritta in caratteri dorati. Sul dorso, quasi in cima, reca l’iscrizione
e verso il fondo la segnatura della biblioteca pubblica di Siena,
Dalle pagine di spessa carta bianca pulita che formano la rilegatura interna si capisce che il volume è stato legato di nuovo da non molto tempo.
Il manoscritto, privo del capitolo 15, è composto da 224 fogli scritti su entrambe le facciate. I numeri di pagina – che vanno da 1 a 224, in cifre indo-arabiche – sono stati aggiunti in seguito sulla parte anteriore di ciascun foglio, in alto al centro. La pergamena è spessa e rigida, ma non fragile. Fatta eccezione per la pagina frontale, che si è in parte disgregata ed è stata attaccata a un foglio di sostegno, le condizioni sono considerevolmente buone. Qualche pagina ha un buco, e i margini di qualcun’altra si sono consumati dopo essere stati sfogliati per più di sette secoli. Molte pagine presentano un colore biancastro, altre sono di un marroncino chiaro e parecchie sono scolorite. Su ogni pagina è stata tracciata con cura una griglia per guidare la scrittura; l’inchiostro del testo è marrone, mentre tutte le cifre sono scritte in rosso. Al principio di qualche paragrafo, la lettera iniziale è più grande e a sua volta in rosso; inoltre, lo scriba ha adornato alcuni inizi di capitoli con grandi lettere stilizzate in blu e oro.
Nonostante i danni, in cima alla prima pagina si legge ancora il titolo originale:
Aritmetica Leonardi Bigholli de Pisa
L’ultima pagina del manoscritto termina con l’iscrizione
Exptir cbet aritmetica Leonardo bigholli de pisa
schiacciata sul fondo.
Il manoscritto di Firenze è custodito nella Biblioteca Nazionale Centrale, che si trova su una piccola piazza sulla riva nord dell’Arno, nel centro della città. Questa copia è notevolmente più sottile di quella di Siena, pur avendo più o meno la stessa altezza e larghezza. La copertina non porta nessuna iscrizione ed è legata al volume con due fermagli di ottone. Le pagine misurano 20 centimetri di larghezza per 30 di altezza, quasi come quelle di Siena; senza contare la copertina, lo spessore del volume è però di soli 4 centimetri, ben uno in meno della copia senese. Ci sono in tutto 213 fogli scritti su ambo le facciate, per un totale di 426 pagine; un numero quasi pari a quello della copia di Siena, quindi, anche se questo manoscritto include il capitolo 15.
Sul lato interno della rilegatura frontale sono incollati due minuscoli frammenti di manoscritto, tutto ciò che rimane della copertina originale. L’unica frase che riesco a capire – e neppure con assoluta certezza – è:
Leonardi Pisani Algorism A[ritm]etica
In cima alla prima pagina del manoscritto si legge la seguente iscrizione:
A C Leonardus pisanus Algorisma & Geometrie est
Abbacie florenty
In genere, il manoscritto di Firenze viene descritto come «molto sciupato»; tuttavia, fatta eccezione per qualche singola pagina (tra cui la prima), io non ho affatto avuto questa impressione. Al contrario, nel complesso le sue condizioni mi sono sembrate molto migliori di quelle del libro di Siena. La carta è secca ma non fragile, e sembra un po’ più sottile di quella della copia senese (il che spiega perché questo volume è molto meno spesso dell’altro, pur avendo un numero di fogli quasi identico). A differenza dell’altro manoscritto, nessuna pagina presenta buchi o margini consunti. L’inchiostro del testo è marrone-nero, mentre le cifre sono tutte in rosso. Lo scriba che ha composto questa copia era senza dubbio quello con il maggior talento artistico: ha decorato i margini di numerose pagine con fantasiose volute e si è servito in misura molto maggiore di elaborate lettere rosse per iniziare i paragrafi e di grandi lettere ornamentali dai colori rosso, blu e oro al principio delle sezioni. Alcune pagine sono di fatto sbiadite, e diverse sono diventate marroni o grigie e mostrano delle macchie. Su alcune di esse si possono ancora vedere le linee guida usate dallo scriba nella stesura del testo. Nel complesso, comunque, si tratta di un manoscritto in ottima forma, considerata l’età.
È strano tenere in mano un libro scritto da un copista medievale più di sette secoli fa, in particolare quando si tratta di un testo che ha giocato un ruolo così importante nello sviluppo del mondo moderno. Conoscevo i suoi contenuti da anni ed ero consapevole delle circostanze che avevano condotto alla stesura del manoscritto, ma fino a quel momento la mia conoscenza si era limitata al piano intellettuale; tenere queste opere in mano, come ho fatto a Siena e a Firenze, era invece un’esperienza fisica, viscerale, era una conoscenza attraverso il corpo e non più solo nella mente. In entrambe le biblioteche, mentre giravo lentamente le pagine, Leonardo e la sua storia acquistavano realtà.
Ogni periodo storico produce degli individui che sono molto avanti rispetto ai loro tempi ma che, tuttavia, appartengono anche alla loro epoca: la prima caratteristica permette loro di immaginare il possibile, la seconda di renderlo reale. Stiamo parlando di figure come Archimede, Copernico, Galileo, Keplero, Newton ed Einstein. Leonardo Pisano, detto Fibonacci, merita di essere annoverato fra di loro. La storia lo aveva quasi dimenticato, fino al punto che di lui era sopravvissuto soltanto un soprannome datogli da uno storico ottocentesco; e anche questo veniva ricordato solo in riferimento a una sequenza di numeri che compare nella soluzione di un problema da lui copiato da un’altra fonte. Nel frattempo, per secoli la sua vera eredità è rimasta indicata in una singola, breve citazione presente in un solo libro (la Summa di Pacioli).
Oggi, però, il nome di Leonardo ha ripreso il posto che gli spetta, a fianco degli altri grandi individui che hanno plasmato il nostro mondo e la nostra stessa identità. In fin dei conti, non c’è bisogno di andare in Italia per vedere il lascito di Leonardo: lo viviamo già ogni giorno, ogni volta che facciamo qualcosa che si basa sull’aritmetica moderna da lui introdotta in Occidente.
A Anche se all’epoca di Leonardo le persone rilegavano i manoscritti «in forma di libri», questi ultimi – a differenza di quello che compare nella statua – non assomigliavano però ai libri moderni.
B Anche se all’epoca di Leonardo le persone rilegavano i manoscritti «in forma di libri», questi ultimi – a differenza di quello che compare nella statua – non assomigliavano però ai libri moderni.

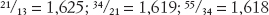 Dato che φ è un numero irrazionale, mentre il numero dei petali, delle spirali o degli stami in una pianta o in un fiore dev’essere un numero intero, la natura «arrotonda» al numero intero più vicino; e, per via della proprietà del limite di cui sopra, quest’ultimo tenderà a essere un numero di Fibonacci.
Dato che φ è un numero irrazionale, mentre il numero dei petali, delle spirali o degli stami in una pianta o in un fiore dev’essere un numero intero, la natura «arrotonda» al numero intero più vicino; e, per via della proprietà del limite di cui sopra, quest’ultimo tenderà a essere un numero di Fibonacci.