Let’s round out this chapter with an example program. Its task is to calculate fib(n) for a list of n, where fib(n) is the nth Fibonacci number. (The Fibonacci sequence starts 0, 1. Each subsequent number is the sum of the preceding two numbers in the sequence.)[33] I chose this not because it is something we all do every day, but because the naive calculation of Fibonacci numbers 10 through 37 takes a measurable number of seconds on typical computers.
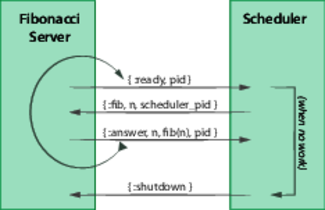
The twist is that we’ll write our program to calculate different Fibonacci numbers in parallel. To do this, we’ll write a trivial server process that does the calculation, and a scheduler that assigns work to a calculation process when it becomes free. The following diagram shows the message flow.

When the calculator is ready for the next number, it sends a :ready message to the scheduler. If there is still work to do, the scheduler sends it to the calculator in a :fib message; otherwise it sends the calculator a :shutdown. When a calculator receives a :fib message, it calculates the given Fibonacci number and returns it in an :answer. If it gets a :shutdown, it simply exits.
Here’s the Fibonacci calculator module:
| | defmodule FibSolver do |
| | |
| | def fib(scheduler) do |
| | send scheduler, { :ready, self() } |
| | receive do |
| | { :fib, n, client } -> |
| | send client, { :answer, n, fib_calc(n), self() } |
| | fib(scheduler) |
| | { :shutdown } -> |
| | exit(:normal) |
| | end |
| | end |
| | # very inefficient, deliberately |
| | defp fib_calc(0), do: 0 |
| | defp fib_calc(1), do: 1 |
| | defp fib_calc(n), do: fib_calc(n-1) + fib_calc(n-2) |
| | end |
The public API is the fib function, which takes the scheduler PID. When it starts, it sends a :ready message to the scheduler and waits for a message back.
If it gets a :fib message, it calculates the answer and sends it back to the client. It then loops by calling itself recursively. This will send another :ready message, telling the client it is ready for more work.
If it gets a :shutdown it simply exits.
The scheduler is a little more complex, as it is designed to handle both a varying number of server processes and an unknown amount of work.
| | defmodule Scheduler do |
| | |
| | def run(num_processes, module, func, to_calculate) do |
| | (1..num_processes) |
| | |> Enum.map(fn(_) -> spawn(module, func, [self()]) end) |
| | |> schedule_processes(to_calculate, []) |
| | end |
| | |
| | defp schedule_processes(processes, queue, results) do |
| | receive do |
| | {:ready, pid} when length(queue) > 0 -> |
| | [ next | tail ] = queue |
| | send pid, {:fib, next, self()} |
| | schedule_processes(processes, tail, results) |
| | |
| | {:ready, pid} -> |
| | send pid, {:shutdown} |
| | if length(processes) > 1 do |
| | schedule_processes(List.delete(processes, pid), queue, results) |
| | else |
| | Enum.sort(results, fn {n1,_}, {n2,_} -> n1 <= n2 end) |
| | end |
| | |
| | {:answer, number, result, _pid} -> |
| | schedule_processes(processes, queue, [ {number, result} | results ]) |
| | end |
| | end |
| | end |
The public API for the scheduler is the run function. It receives the number of processes to spawn, the module and function to spawn, and a list of things to process. The scheduler is pleasantly ignorant of the actual task being performed.
Let’s emphasize that last point. Our scheduler knows nothing about Fibonacci numbers. Exactly the same code will happily manage processes working on DNA sequencing or password cracking.
The run function spawns the correct number of processes and records their PIDs. It then calls the workhorse function, schedule_processes.
This function is basically a receive loop. If it gets a :ready message from a server, it sees if there is more work in the queue. If there is, it passes the next number to the calculator and then recurses with one fewer number in the queue.
If the work queue is empty when it receives a :ready message, it sends a shutdown to the server. If this is the last process, then we’re done and it sorts the accumulated results. If it isn’t the last process, it removes the process from the list of processes and recurses to handle another message.
Finally, if it gets an :answer message, it records the answer in the result accumulator and recurses to handle the next message.
We drive the scheduler with the following code:
| | to_process = List.duplicate(37, 20) |
| | |
| | Enum.each 1..10, fn num_processes -> |
| | {time, result} = :timer.tc( |
| | Scheduler, :run, |
| | [num_processes, FibSolver, :fib, to_process] |
| | ) |
| | |
| | if num_processes == 1 do |
| | IO.puts inspect result |
| | IO.puts "\n # time (s)" |
| | end |
| | :io.format "~2B ~.2f~n", [num_processes, time/1000000.0] |
| | end |
The to_process list contains the numbers we’ll be passing to our fib servers. In our case, we give it the same number, 37, 20 times. The intent here is to load each of our processors.
We run the code a total of 10 times, varying the number of spawned processes from 1 to 10. We use :timer.tc to determine the elapsed time of each iteration, reporting the result in seconds. The first time around the loop, we also display the numbers we calculated.
| | $ elixir fib.exs |
| | [{37, 24157817}, {37, 24157817}, {37, 24157817}, . . . ] |
| | |
| | # time (s) |
| | 1 21.22 |
| | 2 11.24 |
| | 3 7.99 |
| | 4 5.89 |
| | 5 5.95 |
| | 6 6.40 |
| | 7 6.00 |
| | 8 5.92 |
| | 9 5.84 |
| | 10 5.85 |
Cody Russell kindly ran this for me on his four-core system. He saw a dramatic reduction in elapsed time when we increase the concurrency from one to two, small decreases until we hit four processes, then fairly flat performance after that. The Activity Monitor showed a consistent 380% CPU use once the concurrency got above 4. (If you want to see similar results on systems with more cores, you’ll need to increase the number of entries in the to_process list.)