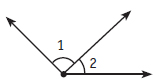
adjacent angles: Angles that share a vertex and a side. Angles 1 and 2 are adjacent.
congruent angles: Angles that have the same measure. The symbol for congruent is ≅. ∠ 3 ≅ ∠ 4
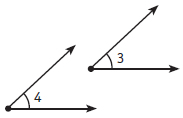
adjacent angles: Angles that share a vertex and a side. Angles 1 and 2 are adjacent.
congruent angles: Angles that have the same measure. The symbol for congruent is ≅. ∠ 3 ≅ ∠ 4
Angles 3 and 5 are congruent. What is the measure of 5?
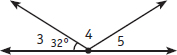
Step 1: What is the measure you are given in the diagram?
Step 2: Congruent angles have the same measure. When you know the measure of one angle, you also know the measure of the other. You know the measure of ∠3, so you know the measure of ∠5.
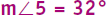
When a question is taking an especially long time, or has you stumped, leave the question and go on. Come back later if you have time. Another question may give you a clue that can help you solve the problem.
Adjacent angles share a side. The sides of ∠ STQ are 
and 
There are two angles shown that sharea vertex and a side with ∠ STQ. Theadjacent angle must be named using three points with the vertex in the center.
What is the measure of ∠ ACD?
Step 1: You are given the measure of ∠ACB and ∠BCD.
m∠ACB = 26°
m∠BCD = 41°
Step 2: You can add the measures of angles that share sides to find the measure of the combined angle.
m∠ACB + m∠BCD = m∠ACD
26° + 41° = 67°
m∠ACD = 67°
complementary angles: Two angles that have measures with a sum of 90°. Complementary angles form a right angle when they are adjacent.
supplementary angles: Two angles that have measures with a sum of 180°. Supplementary angles form a straight angle when they are adjacent.
Some of the answers may look correct if you do not read the questions carefully. In the question above, you could easily choose answer b if you confuse complementary and supplementary.