
We will start by using the Moon’s orbit to find the mass of the Earth. This we do just as a check of the method we will be using for finding the masses of other astronomical bodies, since we have already measured the Earth’s mass using laboratory methods.
We write Mm as the mass of the Moon and Rm as the distance from the center of the Earth to the center of the Moon. Substituting these into the equation for gravitational attraction, we get the value of the attracting force of gravity acting between the Earth and the Moon:

As Newton realized, this must be exactly balanced by the centripetal force pushing the Moon away from the Earth. If the Moon’s period (one month) is Pm, then its velocity in its orbit (taken for simplicity here to be circular) is found by dividing the circumference of the orbit by the period. That is to say,

Then the centripetal force is
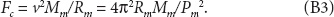
Now, since the force of gravity and the centripetal force must balance, Fg = Fc, we have from (B1) and (B3)
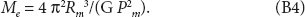
Notice that the unknown mass of the Moon has dropped out of the equation, and we have all known astronomical quantities on the right-hand side. Physically, the fact that our test body, the Moon, has disappeared from our equation is due to the same wonderful fact that Galileo discovered and that Einstein made the cornerstone of general relativity; all bodies fall at the same rate in the same gravitational field, so the motion of the Moon is independent of its mass.
Putting into these equations the period of the Moon’s orbit, one month Pm = 2.4 × 106 seconds, the distance of the Moon from the center of the Earth, Rm = 3.8 × 108 meters, and G from our earlier calculation, we obtain the mass that the Earth must have to keep the Moon in its orbit: 6.0 × 1021 kg. It agrees very well with what is obtained by the Cavendish experiment. We used here the distance of the Moon from the Earth, but this could be (and actually was, by Greek astronomers) determined by elementary geometry; the edge of the Moon, seen at a given time from two different places on Earth, is seen at a slightly different spot in the sky. Then, given the number of miles between the two observers and the angle between the two spots on the sky, the distance to the Moon, in miles, can be computed by elementary trigonometry.
The method outlined above is the fundamental means for almost all determinations of the masses of astronomical bodies. As a first application, we can find the mass of the Sun. The distance between the Earth and the Sun is Re = 1.5 × 108 km, and for the period we use the year, Pe = 3.15 × 10 7s. Plugging these values into equation (B4) we obtain Msun = 2.0 × 1030 kg.
Now let us check if this method is giving a sensible answer. Instead of using the Earth’s orbit, we could take that of Venus, which is closer to the Sun than we are, or the orbit of Mars, which is farther out, and again compute the mass that the Sun would need to keep these planets steadily circling in their orbits. When we do this, we obtain the identical mass for the Sun.
Since our Sun circles around the center of our own spiral galaxy, the Milky Way, we can again use equation (B4) to obtain its mass interior to our orbit. Using for the radius in (B4) the distance from us to the center of our galaxy, 8.5kpc, and for the period, 240 million years, we find a mass equivalent to 90 billion suns inside of our orbit. While this is a large number, it is not unreasonably large compared to the counted number of stars in the southern Milky Way, if we allow for the fact that many are obscured by dust between us and them. Almost all methods of measuring mass in astronomy are variants of these simple calculations.