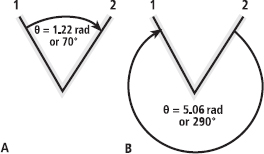
Angles
Angles are defined as the angular variation between two lines or axes, where one line or measurement is designated as the primary. In example A below, the angle (θ) is defined as positive from 1 to 2 in a clockwise direction (‘1’ is the primary line, so the angle is measured from there), whereas in example B the angle is defined as positive from 2 to 1.

FIG. B.1
Calculation of the reverse angle is indicated with a negative sign. For example, the reverse angle in B is equal to -1.22 rad or -70°. There are 6.28 (2π) radians or 360° in a complete circle.
Angular velocity and angular acceleration are also measured in the same way but are the time integrals of angle (i.e. a change in angle divided by the change in time). For example, angular velocity is measured in rad·s-1 or °·s-1 and angular acceleration in rad·s-2 or °·s-2. The frequency with which an object spins is measured as ‘cycles per second’ or hertz (Hz). If an object spins through 6.28 (2π) radians (360°) in one second, it is spinning with a frequency of 1 Hz.
Working with numbers
When trying to solve or understand biomechanics problems, you will often have to work with quantities measured in both the positive and negative directions. So it is important to understand how to do this. Here are the basics:
Adding a negative number is the same as subtracting that number:
8 + -2 = 6
-5 + -3 = -8
2 + -6 = -4
Subtracting a negative number is the same as adding that number:
3 – -5 = 8
-2 – -6 = 4
-9 – -3 = -6
Multiplying or dividing a number of the same sign always gives a positive answer:
5 × 2 = 10
-5 × -2 = 10
15 ÷ 3 = 5
-15 ÷ -3 = 5
Multiplying or dividing a number of the opposite sign always gives a negative answer:
5 × -2 = -10
-5 × 2 = -10
15 ÷ -3 = -5
-15 ÷ 3 = -5
Order of Operations
When you have to calculate an answer to a mathematical problem that has more than one step, you follow a specific set of rules:
Multiply or divide before you add or subtract (unless there are brackets).
2 + 4 × 3 = 14
(2 + 4) × 3 = 18
12 – 4 ÷ 2 = 10
(12 – 4) ÷ 2 = 4
6 ÷ 2 + 4 × 6 = 27
(that is, 6 ÷ 2 = 3 and 4 × 6 = 24, 3 + 24 = 27)
6 ÷ (2 + 4) × 6 = 0
(that is, 2 + 4 = 6 and 6 ÷ 0 × 6 = 0)
Percentages
A percentage is the number of times something would occur if there were 100 possibilities. For example, if a coin if tossed, it is likely to land on ‘heads’ about 1 in every two times or 50 times in a hundred. So, the likelihood is 50% (that is, 50 / 100).
To calculate percentages, divide the number of times an event occurs by the number of times it could possibly occur, then multiply by 100. For example, if you were asked to do 40 push-ups but you only made 28, then you can say you did:
28/40 × 100 = 70% of your push-ups.
If you came back after some training and did all 40 push-ups (that is, 100%) then, by comparison, you’ve done:
(40 - 28)/28 × 100 = 42.9% more push-ups than last time.
Solving Equations (basic algebra)
As you’ve seen throughout this book, we often use equations to calculate quantities that we can’t measure (or haven’t measured). To find a quantity when we have measured other things, we often need to re-arrange an equation. The key to this is that:
Whatever you do to one side of an equation, you must do to the other.
If you remember this advice you can’t go wrong, even if it takes a while to get the answer. To prove this, you can see that writing ‘7 + 2’ is the same as writing ‘5 + 4’, because the answer to both of these is ‘9’. We could also say:
7 + 2 = 5 + 4
You’ll also notice that if I subtract ‘4’ from the right hand side of the equation (so I’m left only with the ‘5’), the equation would no longer be correct, but if I subtract ‘4’ also from the left side of the equation, it becomes correct again:

This works for all equations and can be used to solve equations for which no numbers have been used. For example, if I want to find u in the equation v = u + at, I would do this:

All other manipulations of equations are done the same way but it might take several steps. It is important to do these steps one at a time unless you are a good mathematician. Another tip is that if you are re-arranging an equation to do a mathematical calculation, you should re-arrange the equation before you put the numbers in. Once the numbers are in, you might find it much more difficult to keep track of what you are doing.