Scale, and consequently proportion, as related to representation, has a long tradition of being related to the human body. With the Renaissance, humanist depictions of architectural space were innovatively delimited using linear perspective, in which the rendered image is fixed to a viewer's eye. Perspective remained the primary mode of pictorial representation late into the nineteenth century until another post-humanist, rationalist mode of pictorial representation challenged its authority: the axonometric.1 Axonometric projection is a specific form of parallel projection in which the projectors are perpendicular to the plane of projection. Unlike perspective projection, in which the projectors meet at a fixed point in space, parallel projectors are said to meet at infinity. The three axes of an axonometric projection are uniformly measurable and precisely scaled relative to the axis system's angle of inclination to the picture plane. Many architectural critics assert that meaningful architectural representation was eroded by the technical instrumentality tied to a representation generated by the positivism of science.2 Descartes's philosophy, and his Cartesian geometry, is thought to have objectified the subjective view of the world, so that the individualised, inhabiting, ‘embodied’ viewer was forced into the position of passive, ‘disembodied’ observer (Pérez-Gómez and Pelletier 1997: 313). This chapter counters that position with a critical consideration of the history of axonometry and proposes that Auguste Choisy's inventive development of the worm's-eye view parallel projection is a meaningful, immersive measure of man. Indeed, Choisy uses the subjectivity of his worm's-eye view to impart a sense of our own bodily scale within the measured, spatially materialised boundaries of architecture.
The invention of a modern, post-humanist form of architectural representation – the axonometric – was spawned by William Farish's presentations of mechanical philosophy at the University of Cambridge during the early nineteenth century. Farish devised a kit-of-parts modelling system, and a coincident drawing system, to demonstrate the principles of Newtonian mechanics. Farish's drawing system, called ‘isometrical perspective’, was developed in order to record the temporary demonstration apparatus. Farish publicly introduced his formal discourse ‘On Isometrical Perspective’ to the Cambridge Philosophical Society in 1820, and the essay was published in their Transactions in 1822. Farish observed that while plans, sections, and elevations are measured and accurate, they do not allow a construction to be understood as a three-dimensional entity in space. Conversely, common perspective distorts the reality of the object, since parallel lines are not represented as parallel and there is no measurable scale. Farish's isometrical perspective combines the useful attributes of orthographic and perspective projections.
Isometric literally means equal measure, and Farish indicated that the term describes a cube represented so that the three principal faces make equal angles with the picture plane, and consequently all have the same scale. The author acknowledges that isometric perspective is not a perspective, but corresponds to the function of a perspective by rendering a pictorial view. The eye of the artist is placed at an indefinite distance, rather than at a fixed vanishing point; thus, the projectors are parallel. Farish assumed a bird's-eye view that also instils a sense of distance. Regardless of his expressive terminology, Farish understood isometrical perspective as a ‘species of orthographic projection’; the projection is on a plane perpendicular to the diagonal of a cube (Farish 1822: 5–6). In terms of architectural representation, the successive developments of this new form of projection lead to a modern spatial visioning system with determined scale.
Farish's method was taken up by German engineers, geometers and mathematicians. In 1844, Julius Weisbach published the critical geometric, trigonometric evolution of isometry towards axonometry in ‘Die monodimetrische und anisometrische Projectionsmethode (Perspective)’. In addition to building on the many isometrical methods successive to Farish, Weisbach expanded on the nomenclature and theories of crystallography proposed by Carl Friedrich Naumann in 1830. Naumann's theory linked the inherent axial structural forms of crystals to their appropriate graphic representations.
Weisbach established a projective axis system by theorising that points could be projected by their coordinates on axial planes (Meyer and Meyer 1863: 13, n1). Thus, the orientation and reduction of the axes did not have to stay isometrically inclined and equally reduced. The coordinate axes could be reduced in scale relative to their angles of inclination; Weisbach qualified these scaling conditions as monodimetric (in the case in which two axes are equally reduced) or anisometric (in which all three axes are differently scaled). While Weisbach differently coordinated the space of the isometric, he did not use the term axonometric to encompass the newly defined axial projections. This appears to have occurred eight years later, in 1852, in a work by the Meyer brothers of Freiburg.3
The Meyers proposed in their Lehrbuch der axonometrischen Projectionslehre that Weisbach's measured and scaled axis system, comprising isometric, monodimetric, and anisometric projections, be named axonometry, and that the method be called axonometric projection. Whereas Weisbach's work was exclusively theoretical, Meyer and Meyer comprehensively explored axonometric projection's theory and practice through its history, aesthetics, geometry, mathematics, process and application. They advanced a method by which to construct axonometric projections in space; the representation is bound to axiality. Their axonometric drawing method is demonstrated by first determining the desired orientation of the axonometric axes, and by consequence the orientation of the rotated or revolved object in space.
Like Naumann and Weisbach before them, the Meyers advocated that the nature of the object should influence the orientation of the axis system to the picture plane, and thus to its representation. To establish the orientation of the axis system, the object is imagined as to how it naturally falls into the picture, or projection, plane. They clearly asserted that maintaining this natural aspect would more closely approximate the image as one receives it to the eye, the first prerequisite for image-making (Meyer and Meyer 1863: v). The vertical axis coordinate plane typically stays vertical as it is equated to gravity; it measures height. The perpendicular, horizontal planes naturally correspond to the plan; these coordinate planes are parallel to its length or width. They observe that the easily constructed and accurate isometric system can be an awkward representation for some objects due to its prescriptive, inclined, often bird's-eye view (Meyer and Meyer 1863: vi). The natural relation of the object to the eye is not considered in the isometric due to its completely systematic application. The Meyers believed that a more complete expression is offered by the monodimetric and anisometric axis systems, which support a closer interaction between observer and object through the selective rotation of their axes.
The Meyers elaborate that establishing a point of view in axonometry does not conclude with the selection of an axis system. Within the same axis system and scaled ratio of reduction, there can be various points of view. The inherent revolving spatiality of the parallel, axonometric axis system allows reversibility; they state that ‘one can also exert an inverse bias with this axis system, so that the observer may see into the system as at an angle or from below’ (Meyer and Meyer 1863: 50).4 Accompanying figures of monodimetric representations of a cube demonstrate the potential for transpositions within the same axis system and the same ratio via the axonometric lines; first they are articulated forward, then backward. It is within the context of a perspective and monodimetric comparison that we see the Meyers’ only up-view representations. The reverse axis, the same monodimetric relation as that conveyed in the aforementioned demonstration cube, is used to convey a comparable image to an up-view perspective of an Ionic entablature. The Meyers conclude that the two rendered impressions are similar, but the tectonic, axonometric view is more multivalent than that tied exclusively to the eye.
Finally, the brothers maintain that the axonometric method is not only a means by which to manifest an image of real bodies in a single picture, but that the picture has the same effect as the object itself (Meyer and Meyer 1863: v). Meyer and Meyer contend that the axonometric is truly spatial. Points, lines, surfaces and bodies as located in space are projected onto one picture plane (Meyer and Meyer 1863: 1).5 The scaled values of true form and size are juxtaposed in space. Under axonometric projection, the figurative representation on the plane of projection allows one to understand the true spatial nature of bodies. Meyer and Meyer liken this spatial view of parallel projection to that of conic perspective. The Meyers convincingly argue that central perspective, called the ‘painter's perspective’, finitely restricts the image to the eye; whereas axonometric projection, by virtue of its true parallelism in infinite space, ‘allows the eye to hover at each single point’, and is thus liberated and imaginative (Meyer and Meyer 1863: 1).6 One can perceive that the invented views fabricated by axonometric projection are contingent on a different, modern conception of the object and man in space.
The Meyers’ work was followed up by another study by Julius Weisbach (1857). While much of the material closely parallels that of the Meyers, there is a note of originality: the demonstration of the projection of axonometric shadows. This application firmly establishes the axonometric's place as a method of representation, and not merely a mathematical or geometrical operation.7 The interjection of shadow links axonometry to the world of optic projection, thus embodying the subjective scale of man as a measurable quality within the mathematical space of parallel projection.
The Meyers’ articulation of varied points of view is a critical turn tied to the axonometric's development. The bird's-eye view had been an implicit convention of early parallel projections; the overview tied by Farish to isometric projection was preceded by that of oblique projection.8 During the sixteenth century, the mechanisms of war depended on measured precision and the art of fortification became the vehicle for oblique projection's first analytical articulation.9 Military (from the plan) oblique projections were conceptually tied to an overview of the horizontal plane through the orthogonal plan and its volumetric extrusion. The Germans alternatively referred to the cavalier (from the face) oblique projection as a Vogelperspektive, a bird's perspective. The practice was maintained with the invention of isometry. Farish's convention assumed the perspective normatively from a bird's-eye view and this premise was maintained by his followers, including Jopling, who maintained a bird's-eye view as he positioned geometric solids within a static isometric cube-frame (Jopling 1842: 18–20). The underside is depicted by rotating the object, not the bird's-eye position of the observer. In most cases, the bird's-eye view was assumed. Weisbach and the Meyers all commented on the alien up-standing view accorded to isometrical projection. The early convention of parallel projections, oblique or isometric, held the observer at a distance, defining the object by a summary overview.
The up-view parallel projection evolved as a natural extension of axonometry's rotational freedom and the need to overtly posit a point of view. Axonometric space allowed architectural spaces to be technically scaled and materialised relative to a positioned observer. The geometric shift from the isometric cube to the axes of coordinates stimulated reinterpretations of all parallel projections, axonometric and oblique. The potential of this spatial, rotational freedom relative to architectural representation was first extensively investigated by the French engineer Auguste Choisy during the late nineteenth century. In his first published work, L'art de bâtir chez les Romains (1873), one can see the manipulation of axonometry's varied but specific axial revolution and its inherent reversibility.
Choisy had a clear intention in this book to express graphically the spatio-tectonic nature of Roman vaulted construction; however, he could not tectonically and spatially explicate the effect of Roman vaults from above. Choisy observed that the primary material structure of Roman vaulted construction consisted of an ‘encased framework in a mass of masonry’ (Choisy 1873: 3).10 Tectonically speaking, the lower, inside surface is where the embedded framework, this essential component, is structurally expressed, as well as the enclosing space of the vault itself containing the body of man. The necessitating nature of the Roman tectonic, combined with the spatio-geometric potential of axonometry, appears to have led Choisy to revolutionise the tectonic vision of parallel projection via a view from below.
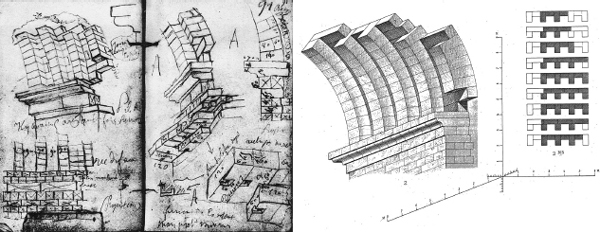
The Romains was the result of meticulous, measured, minute observation of physical and textual sources, from which evolved Choisy's theory of form. We gather an impression of Choisy's early field methods through his sketches in his ‘carnet de mission de 1867’: two pages depict the bridge of Narni in Umbria (Figure 1, left). The focus of the sheets seems to lie in the relation of the discrete stones to a composite whole. The individual travertine blocks are measured, carefully positioned within the scaled assembly, and shown rising into an arc. The stacked stones are seen from below, as undoubtedly seen by Choisy, from the ground. Written on the underside of the enlarged detail in the lower right corner is the word dessous, or underneath. Here one sees the tectonic origins of axonometry's worm's-eye view. The material matter of architecture rises to delineate a habitable space. The fully developed worm's-eye views will make that tectonic space manifest.
The compiled sketches essentially revolve around the springing of the arch, collecting views in a 180° rotation around the object. These views of the pier coalesce in the Romains into one pictorial, yet precisely scaled, oblique projection, and a diagram superimposing horizontal sections of the vault ribbing (Figure 1, right). The clean extraction of such tectonic fundaments will come to define Choisy's earliest work. In Choisy's sketches and drawing, we can see the relationship between this constructive logic and the worm's-eye view. The observer inhabits the space under the vaults of the Roman engineers; the structure builds from the earth to the sky to delimit architectural space. The up-view is phenomenally paramount.
Among the many graphic attributes, the most consistent device in the plates of the L'art de bâtir chez les Romains and its successor, L'art de bâtir chez les Byzantins (1883) is the use of the worm's-eye view parallel projection. In the Romains, the up-view is applied to all forms of parallel projection: isometric, dimetric and trimetric axonometrics, and oblique projections from the plan and elevation. There appears to be no system. The types and angles of projection are diverse. Perhaps following the recommendation by the Meyers, Choisy adjusted each viewing angle to that which best expressed the object to the observer. The up-view encloses the viewer in the space of the vault and Choisy's first step to achieve this is to establish the directions of the projections of the axes. Fundamentally, this subjective decision orients the viewing angle of the object. Subsequently, the relative reductions of the scales of each inclined axis are determined via projection. The resultant representation is a true measure of the object, and man, in space.

Figure 1 Left: bridge of Narni in Umbria from Choisy's sketchbook, 1867 (Royer 1960: Plate 2). Right oblique projection from the elevation (Choisy 1873: Plate XVI, detail).
Choisy suggests that his parallel projections serve an intentioned dialectical purpose by positing the vaulted artefacts as concrete realities and as a mental construct (Choisy 1873: ‘Note sur le mode de représentation adopté’). Multiple graphic qualities frame a dual reading of these images. The realm of the discovered, extant and documented ruin is upheld through the depiction of overgrown vegetation, shadows and, in a few instances, representations of sky or ground. The shadows evoke a picturesque variety expressing the remnant as a focal point and located to one moment in time. Such environmental renderings reflect one of Choisy's self-imposed rules, ‘to make known the antique construction by personal observation of the monuments’ (Choisy 1873: 84–5).11 Other graphic details also point towards the found condition of the monuments. The arches and vaults are limited to fragments, like the ruins themselves. In some cases, each side of an arch springs into the air, but is truncated, no longer connecting to its counterpart (Figure 2). Such shards evoke a complete entity, thus animating the past. The monuments are also depicted denuded of decoration, and so the material essence is excavated for study. The rendered surfaces of this material structure are shown with delaminating surfaces, protruding bricks and, in one or two cases, frayed, crumbled edges. Despite the fact that Choisy did not reproduce the actual state of the ruin, his drawings demonstrate through these atmospheric treatments an inherent natural beauty found in the structural remains of architectural form.
Concurrently, some of the same drawing components portray the core relic as a prospective model. The ideal realm of the structure of the past is scaled, in part, by Choisy's use of construction lines. The latent rational structure of the remnants of the past is delimited and extrapolated with such graphic tracings. These lines variously abstract geometric, material, graphic and quantitative information, and are also instrumental, constructive elements. The found remnant is largely dissected in a clean, pure manner; sectional cuts are typically blank voids delineated by hard edge lines. At times, the rendered material surface wraps into the sectioned plane, yet the material element, typically brick, is distilled to its outline. The graphic extension of the material is always partial, but each material element is always maintained by its standard dimension. Shadow lines banish ambiguity and embody qualitative space within the orthogonal constructs. Other lines, sometimes dashed, extend into space to render an outline of a complete tectonic structure. The materially ruptured vaults of the Palatine Hill are completed through delicate trajectory lines connecting across the spatial gap. These traces geometrically conceptualise the determinant growth of the particular constructive process. Still other lines circumscribe the pure circular geometries ordering many of the vaulted forms. Of course, each representation is accompanied by axial scales of measure. These intersecting lines correspond to and scale the three dimensions of the object. Pragmatically, the establishment of the three-dimensional scale is the initial act of the drawing's projection, but within the static frame of the finished drawing, the axes blatantly posit the architectural artefact as inseparable from its measured, material three-dimensionality. Juxtaposing these axial lines of infinite space with the essential tectonic core also advances a conceptualisation of a progressing constructive extension into three-dimensional space. The abstracting nature of these various regulating lines is instrumental in modelling the prospective, ideal constructive scale of the archaeological artefact.

Figure 2 An up-view, diametric axonometric projection (Choisy 1873: Plate I).
The drawn and traced boundaries of the artefact are informed by the necessary structure. The essence of the system exposes each building's pure core. Choisy individualises the graphic technique to overtly reveal the varied complex of constructive scales in the tectonic fundament: from individual material elements, combinatory systems, structured assemblages, to functional arrangement. The material element is an ideal unit. A tile or brick, measured and put into place by the hand of man, is always drawn as a complete constructive part. Even when the rendered material surfaces are delaminated, the peeled-away layers always respect the material unit. This accentuation of the essential material constituent is also manifest through selective, spatial protrusions, with small elements operating at a subsequent scale, structuring various constructive systems to fulfil formal arrangements. The extent of the represented core assembly is complete when the complete spatial order is inferred. The formal plates of the Romains and Byzantins offer a simultaneous vision of the structural fragment in a state of retrospect and prospect; the essential core is concurrently a sited ruin, as seen in the documentation of the extant, materially scaled remains, and a potential mechanism, as indicated by scalar units of construction and lines of abstraction, including first and foremost the fundamental axial scale of infinite measure.
After the 1873 and 1883 publications of the L'art de bâtir series, a great part of Choisy's research efforts were devoted to the development and production of his most noted work, the Histoire de l'architecture (1899), a historical account of architecture from prehistory to the early nineteenth century.
Choisy's sketches from 1885 reveal the nature of the evolution in his use of parallel projection for the Histoire. His travels that year are represented by sketches of the churches of Saint-Etienne of Nevers, Saint-Savin on the Gartempe and Notre-Damela-Grande of Poitiers. Within the pages of the Histoire, all three buildings similarly represent a stage in the formal progression of Romanesque architecture. However, there are noticeable differences among their sketched representations. The sketch from Nevers is raw. Both the textual and the graphical notations are smudged by an error and reflect a correction. The line work of the sketch is loose, perhaps even inaccurate. The viewpoint is from below and the view conveyed is of the apparent scene, like that of the visitor standing in the nave or perhaps sitting at a pew and looking up. The sketch shows an on-site impression of the structure.
The other, paired sketchbook pages from 1885 contain a study of Saint-Savin on the left page and Poitiers on the right, facing page; both sketches approximate to canonical isometrics. Furthermore, they are both up-views, like the sketch from Nevers. Unlike Nevers, the viewpoint is more analytical; it moves below the horizon line and the constructive elements are suspended in space. Under this aspect, these two sketches, of Saint-Savin and Poitiers, are unique. They clearly hint at the synthetic potential of the worm's-eye view as ultimately realised. There are no other extant sketches that so closely correspond to their future, final composition as published in the Histoire 14 years later. One can easily speculate that these juxtaposed sketches formed a prototype and reflect Choisy's proposed, and ultimate, comparative format for the Histoire. Between the sketch and the illustration, the chronological adjacency, viewing angle and level of detail remained virtually unchanged, whereas the form of parallel projection is changed, from isometric axonometric to oblique projection. One can reasonably draw the conclusion that Choisy's transition from axonometric to oblique projection in this case is fully intentional, and that each drawing system was to be used for particular ends in the Histoire de l'architecture.
One discerns different intentions behind Choisy's use of parallel projection in the L'art de bâtir chez les Romains versus L'histoire de l'architecture. Choisy's later drawings appear to challenge their instrumental, geometric, technical lineage and evince a modern view of the spatial simultaneity of architectural phenomena. The worm's-eye view oblique projections in the Romains and Byzantins typically sprang from a horizontal section above the ground plane, not from a plan. These up-view drawings detailed the technology of the fragment and were limited to explicating particular vaulted conditions built into space. The case of the particular was illustrated. It was not until the Histoire that the structural element was posited in direct relation to its composite structure, which is determinant of the whole form. This shift relates to the up-view moving from a more pictorial viewpoint to a completely imaginary position below the horizontal ground plane. Such worm's-eye views still examine structural elements in the Histoire, but with regard to their essential contribution within a system explicitly determinate of the whole space.
While the drawings of the Romains and the Byzantins overtly straddle the function of retrospect and prospect through their scientific control of graphic, analytic methods, so too do those of the Histoire. However, an evolved conformity of method was used to scale and discriminate essential differences. Different rendering techniques, more abstract in nature, aid the comparative reading of architectural form. Unlike Choisy's drawings in the Romains and Byzantins, the oblique and axonometric drawings in the Histoire are not projections. The drawing systems have been distilled almost exclusively to military oblique projections or canonical isometrics. This is subtly indicated by the disappearance of the axial, spatial scale for each dimension and its replacement with a single dimensional scale for all three. Furthermore, the illustrative, individualised representations of the Romains and Byzantins became necessarily abstracted to posit a conceptualised theory: rendered materiality is shifted to a structural framework, the temporal shadows are replaced by academic poché, the fragment of the ruin becomes a module of design, and the subjective orientation of three-dimensional axes is supplanted by the repeated system of the worm's-eye view oblique projections. The history of architectural form is all the more imaginatively scaled through rational and scientific techniques.
In using oblique projection, Choisy's new methods transformed the artefact into a graphic tectonic language (Figure 3, left). This was largely achieved when the measured uniformity of the conventional plan was combined with uniformly applied rendering techniques that reinforce the comparative nature of the similarly oriented, successive worm's-eye view oblique projections. With oblique projection, there is simultaneity between the geometric purity of the plan, and its proportions and geometry, as juxtaposed with the spatial organisation of the structure. Not only does the up-view animate the structure above our heads, but the worm's-eye view grounds the architecture to its organising plan. Though the ground plan is invisible to the inhabitant, it determines with precision the quality of the spaces we inhabit. The dissection and abstraction in the Histoire became an intellectual method of discursive thought, as a means of hypothesis. The deconstruction indicated construction. The scalar purification of parts, elements, modules, proportions, hierarchies, bays and systems indicates a reverse process, one of building. Thus, Choisy defied the general trend of separating the real from the imaginative. He used the synthetic simultaneity of the oblique projections symbolically, to represent building, in addition to buildings.

Figure 3 Left, worm's-eye view, plan-based, oblique projections convey the spatio-tectonic progression of Greek, Romanesque and Gothic architecture (Choisy 1899).Top: Paestum, Olympia, Selinunte, Parthenon (figs 7, 8, 10, 11). Middle: St Savin, Poitiers, Parthenay, Issoire (figs 11, 12, 13, 16).Bottom: Noyon, Paris, Bourges, Langres (figs 6, 7, 8, 10). Right, worm's-eye view, isometric drawing of Hagia Sophia, Constantinople (Istanbul) (Choisy 1899: Vol. II, 49).
Whereas the oblique projections are grounded by their scaled orthographic plans, the few axonometric projections show free, floating images, somewhat detached from the ground plane (Figure 3, right). The building in space and the space of the building are animated via the skewed view of the axonometric ground plan. The axonometric's explicit warped view was intentionally used by Choisy to animate his graphic visualisations. Isometric projections evidence the harmonic totality and uniform spatial extension of the unified structure of domed spaces, such as Hagia Sophia in Salonica and Constantinople. Choisy considered that the whole composition grouped itself around the dome (Choisy 1899: v. 2, 47–8). He wrote of Salonica, ‘the whole system of equilibrium is inside; all the dispositions are considered in light of supporting and accompanying the dome: the ensemble, in which each part is subordinate to this principal reason, produces an impression of striking clarity’ (Choisy 1899: v. 2, 48).12 The constructive ensemble and the space under the dome are impressed upon the viewer when the spatial simultaneity of the worm's-eye view axonometric brings us inside. One has the distinct sense that one is within the space, bounded by its concrete surfaces and held by the dome. Unlike the drawing, the body of man is not free-floating; it is relationally contained within the spatio-tectonic boundary by the worm's-eye view.
The axonometric drawing models the spatial and tectonic reality of architecture. The subjectivity of the worm's-eye view pulls the viewer into the space of the building. Such rational, scaled drawings denote the spirit of architecture's essence – the space of the structure and the space of man.
1 A more detailed, published explication of the distinct history of oblique and axonometric parallel projections can be found in my article, ‘Revolutions in space: parallel projections in the early modern era’ in arq, vol. 12, no. 3–4, 2008.
2 For example, see Pérez-Gómez and Pelletier (1997) and Bois et al. (1979).
3 Meyer and Meyer's work was first published serially between 1852 and 1855, Lehrbuch der Axonometrie: Lief. I (1852), Lief. II (1853), Lief. III (1855), and eventually published together in 1863.
4 ‘Dass man auch bei diesen Axensystemen eine Neigung nach hinten vornehmen kann, so dass der Beschauer gleichsam schräg von unten in das System sieht, bedarf seiner weiteren Erwähnung.’
5 ‘Die räumlichen Grössen (Linien, Flächen und Körper).’
6 ‘Malerperspective’ … ‘Bei welcher das Auge über jedem einzelnen Punkte stehend.’
7 As asserted by Loria (1921: 419).
8 Oblique projection is an older class of pictorial parallel projection. One trait that overtly divides oblique from axonometric projection is that oblique projection has both two-dimensional and three-dimensional space attributes. Oblique projection presents an aspect of two-dimensional geometric purity as one plane of the object lies parallel to the picture plane. Depth is indicated in an act of oblique extrusion.
9 See Maggi and Castriotto (1564).
10 ‘Cette ossature empâtée dans le corps des maçonneries.’
11 ‘Pour rester entièrement fidèle à la règle que je m’étais imposée, de faire connaître la construction antique par l'observation personnelle des monuments …’
12 ‘Tout le système d’équilibre est intérieur; c'est en vue de maintenir et d'accompagner la coupole que toutes les dispositions sont ménagées: l'ensemble, où toutes les parties se subordonnent à ce motif principal, produit une impression d'une saisissant netteté.’