Reverse Polish Notation (RPN), and it is also known as postfix notation. In RPN, the operators follow their operands, and mathematical operations such as 3 + 4 or 4 * 3 + 2 are written as 3 4 + and 4 3 * 2 +. At first glance, it might look counterintuitive, but it's really handy once you get used to it. One useful advantage of an RPN calculator is that it's easier to solve nested operations with it. It's easier because it doesn't need to use parentheses to resolve the logical priority between operations.
For example:
3 * ( 2 + 5) must be written as 3 2 5 + *
The mechanic is based on the concept of stacking: each operand is added to a stack. When an operator is inserted, like add, multiply, divide or subtract, it is applied to the two topmost operands. The result is put on the top of the stack.
Let's look at a graphical example for solving the previous operation. Before the first operator, we have the following stack:
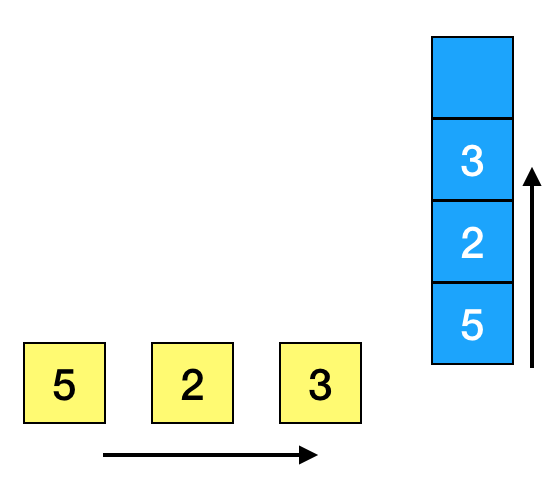
When we insert the +, we sum the two operands on top and push the result on the stack:

Then, for the multiplication, we do the same thing and we finally have our result on the top of the stack:
