CHAPTER 11

Data Sufficiency

Is the product of x, y, and z equal to 1?

(1)     x + y + z = 3

(2)     x, y, and z are each greater than 0.

Above is a typical Data Sufficiency question. In this chapter, we’ll look at how to apply the Kaplan Method to this question, discuss how to tackle this question type, and go over the basic principles and strategies that you want to keep in mind on every Data Sufficiency question. But before you move on, take a minute to think about what you see in this question and answer some questions about how you think it works:

PREVIEWING DATA SUFFICIENCY

How Is the Structure of This Question Different from That of a Typical “Math” Question?

The problem starts off with the question stem, which asks whether the product of x, y, and z equals the value of 1. But then there’s no other information in the question stem. So how are you supposed to answer the question? A Data Sufficiency question stem will never give you enough information to solve for an answer, which is very different from typical math problems. You’re probably used to having a lot of information presented up front, followed by the actual question. But Data Sufficiency works differently: the other data are presented after the initial question; these are called the “statements.” Your goal in a Data Sufficiency question is to determine whether the data in the statements are enough to allow you to answer the question.

Sound unusual? Absolutely. Data Sufficiency is unique to the GMAT—no other standardized test presents questions in this format. Confusing? It doesn’t have to be. As just noted, all you need to do is determine whether the data are sufficient to be able to answer the question. What is not your goal? To do a lot of time-consuming calculations. Business schools don’t care about how many advanced math classes you took. They care about something else: they want to know that you’re able to assimilate a lot of information and make deductions from that information. Many Data Sufficiency questions can be solved without finding the specific answer to the question presented in the stem.

What Mathematical Concepts Are Tested in This Question?

At first, it appears that this question tests only some fairly basic arithmetic concepts: namely, multiplication (in the question stem), addition (in the first statement), and inequalities (in the second statement). But as is often the case on GMAT Quantitative questions, what’s not stated is also important. This is not merely an arithmetic question. It’s testing number properties: how numbers with certain characteristics behave in predictable ways. A careless test taker might take for granted that x, y, and z are integers. But unless the question stem says so, never assume that variables must be integers—or even positive numbers, for that matter. Training your mind to think like this on the GMAT will take time and practice, but using the Kaplan Method for Data Sufficiency and remembering how to apply the Core Competencies will help you through even the toughest Data Sufficiency questions.

How Can You Use the Answer Choices to Your Advantage?

Earlier you read that Data Sufficiency questions don’t necessarily require you to solve the problem. This is because the answer choices are in a fixed format. All five of the answer choices have to do with the “sufficiency” or “insufficiency” of the statements. In other words, does one of the statements alone provide enough information to answer the question? Do both of them? Do both of them, but only when combined? Or is there just not enough information? Again, the answer choices will never give you actual values or expressions, such as “35,612” or “4x3 − 15y.” We’ll show you how to use this fixed format to your advantage.

What GMAT Core Competencies Are Most Essential to Success on This Question?

For all Data Sufficiency questions, Critical Thinking is crucial. Mastering the format and structure will put you at an advantage over your competition, since Data Sufficiency is notoriously one of the greatest challenges for most GMAT test takers. By understanding how these questions are constructed and what the potential traps are, you will know how to get at the heart of what the testmakers are asking you to do.

Attention to the Right Detail is also key to your success on Data Sufficiency. Most importantly, don’t fail to consider the details that aren’t mentioned or the restrictions that don’t exist. Never assume anything in a Data Sufficiency question.

Here are the main topics we’ll cover in this chapter:

QUESTION FORMAT AND STRUCTURE

The instructions for the Data Sufficiency section on the GMAT look like this:

Directions: In each of the problems, a question is followed by two statements containing certain data. You are to determine whether the data provided by the statements are sufficient to answer the question. Choose the correct answer based upon the statements’ data, your knowledge of mathematics, and your familiarity with everyday facts (such as the number of minutes in an hour or cents in a dollar). You must indicate whether

Note: Diagrams accompanying problems agree with information given in the question but may not agree with additional information given in statements (1) and (2).

All numbers used are real numbers.

The GMAT is the only test featuring Data Sufficiency questions, and beginners often misunderstand the format. On the Quantitative section, you’ll see about 15 Data Sufficiency questions, which ask you to assess whether certain statements provide enough information to answer a question. Often the question requires little or no mathematical work. The key to solving the question is understanding how the question type is structured and using that knowledge to work efficiently.

The directions may seem confusing at first, but they become clear with use. Let’s walk through a simple example:

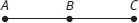
image

What is the length of segment AC?

(1)   B is the midpoint of AC.

(2)   AB = 5

The diagram tells you that there is a line segment AC with point B somewhere between A and C. You’re asked to figure out the length of AC.

Statement (1) tells you that B is the midpoint of AC, so AB = BC and AC = 2AB = 2BC. Since Statement (1) does not give an actual value for AB or BC, you cannot answer the question using Statement (1) alone.

Statement (2) says that AB = 5. Since Statement (2) does not give you any information about BC, the question cannot be answered using Statement (2) alone.

Using both of the statements together, you can find a value for both AB and BC; therefore you can solve for the length of AC, and the answer to the question is choice (C).

THE KAPLAN METHOD FOR DATA SUFFICIENCY

This Method is the essential systematic approach to mastering Data Sufficiency. Use this approach for every Data Sufficiency question. It will allow you to answer questions quickly and will guarantee that you avoid the common Data Sufficiency mistake of subconsciously combining the statements instead of considering them separately at first.

The Kaplan Method for Data Sufficiency

1.  Analyze the question stem.

  • Determine Value or Yes/No.

  • Simplify.

  • Identify what is needed to answer the question.

2.  Evaluate the statements using 12TEN.

Step 1: Analyze the Question Stem

There are three things you should accomplish in this step:

Don’t rush through this step, even for seemingly simple questions. The more you glean from the question stem, the easier it will be to find the right answer.

Step 2: Evaluate the Statements Using 12TEN

Since the answer choices depend on considering each statement alone, don’t let the information you learn from one statement carry over into your analysis of the other. Consider each statement separately, in conjunction with the question stem. Remember that each statement is always true. Don’t waste time verifying the statements; just evaluate whether this information lets you answer the question.

On Test Day, you don’t want to spend even a second reading the answer choices or thinking about which answer choice is which. They will never change, so you will save yourself much time and confusion by memorizing what the answer choices mean and working with them until you’ve fully internalized them.

A helpful way to remember how the answer choices are structured is to use the acronym 1-2-TEN.

1    Only Statement (1) is sufficient.

2    Only Statement (2) is sufficient.

T    You must put the statements together for them to be sufficient.

E    Either statement alone is sufficient.

N    Neither separately nor together are the statements sufficient.

In fact, it’s so important to memorize the answer choices that after this initial sample question, we will no longer print the choices along with the questions. For each practice question, you should follow the routine you will use on Test Day: write 12TEN in your scratchwork for each question and cross out the incorrect answer choices as you eliminate them. We’ll teach you patterns for eliminating answer choices later in this chapter.

Now, let’s apply the Kaplan Method for Data Sufficiency to the question you saw at the beginning of this chapter:

Is the product of x, y, and z equal to 1?

(1)   x + y + z = 3

(2)   x, y, and z are each greater than 0.

Step 1: Analyze the Question Stem

This is a Yes/No question. If xyz = 1, then the answer is “yes.” If xyz ≠ 1, then the answer is “no.” Either answer—“yes” or “no”—would be sufficient. There’s nothing that needs to be simplified in this step; all variables are in their simplest terms, and there are no common variables to combine. It’s often worth thinking about how you could get the “yes” or “no” that you’re looking for. For instance, if x, y, and z all equal 1, you would get an answer of “yes.” But is this the only way? This question is short but definitely not simple, since there may be many other possibilities to consider.

Step 2: Evaluate the Statements Using 12TEN

Picking Numbers for Statement (1), you can readily see how to get a “yes”: x = 1, y = 1, and z = 1. Can you Pick Numbers in such a way that the sum is 3 but the product is not 1? Not if you only consider positive integers. But if you consider different kinds of numbers, you can easily find some. Zero doesn’t alter a sum, but it forces a product to be 0. So x = 3, y = 0, and z = 0, while they follow the restrictions given in Statement (1), will give you an answer of “no” to the original question. Since you can get both a “yes” and a “no,” Statement (1) is insufficient. Eliminate (A) and (D)—or choices “1” and “E,” if you’ve written 12TEN in your scratchwork.

Now that you’ve reached a verdict on Statement (1) on its own, completely put Statement (1) out of your mind as you evaluate Statement (2) independently. Statement (2) rules out the possibility of using 0 but not the possibility of using fractions or decimals. So x = 1, y = 1, and z = 1 is also permissible here, but so is something like x = 100, y = 100, and z = 100. So xyz could equal 1, but it could also equal 1,000,000. So you can get both a “yes” and a “no” here, as well. Statement (2) is also insufficient, so you can eliminate (B)—which is the “2” of 12TEN.

Since each statement is insufficient on its own, you need to consider them together. Can you pick numbers that add to 3 and are all positive? Again, x = 1, y = 1, and z = 1 makes the cut and answers the question with a “yes.” Can you think of numbers that don’t multiply to 1 that also are consistent with both statements? Once again, you have to expand your thinking to include other types of numbers besides positive integers. Fractions and decimals make things bigger when added but smaller when multiplied. For example, x = 2.8, y = 0.1, and z = 0.1 fit the bill. They are all positive and sum to 3. Their product is 2.8(0.1)(0.1) = 0.028; this answers the question with a “no.” Since you can get both a “yes” and a “no” answer, the statements are insufficient to answer the question even when combined. The answer is (E)—which corresponds to the “N” of 12TEN.

Now take a few minutes and answer the questions in the following practice set. Don’t worry if they’re challenging at first; you’re only getting started working with this unique question type. For now, do not concentrate on speed—or even on getting the correct answer in the end—but rather on building your technique for approaching Data Sufficiency questions systematically using the Method. You’ll get much more practice with these questions throughout the chapter.

Practice Set: The Kaplan Method for Data Sufficiency

Answers and explanations at end of chapter

  1. If x > 0, what is the value of x?

    • (1)   x > 5

    • (2)   40 − x2 = 4

  2. If a > 0, b > 0, and 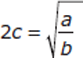image, what is the value of b?

    • (1)   a = 8 and c = 2

    • (2)   image

  3. Team X won 40 basketball games. What percent of its basketball games did Team X win?

(1)   Team X played the same number of basketball games as Team Y.

(2)   Team Y won 45 games, representing 2.5 percent of the basketball games it played.

  1. If 2b − a2 = 18, what is the value of b?

    • (1)   a2 = 1,156

    • (2)   a > 0

  2. A certain company produces exactly three products: X, Y, and Z. In 1990, what was the total income for the company from the sale of its products?

(1)   In 1990, the company sold 8,000 units of product X, 10,000 units of product Y, and 16,000 units of product Z.

(2)   In 1990, the company charged $28 per unit for product X and twice as much for product Z.

THE BASIC PRINCIPLES OF DATA SUFFICIENCY

Especially because this question type is more abstract than Problem Solving, it’s essential to have a strategic approach to every Data Sufficiency question. Don’t waste time or mental energy doing unnecessary calculations. A systematic approach will ensure that you find the most efficient solution to the problem and that you make as few careless and avoidable errors as possible. Here are some ways you can optimize your Data Sufficiency performance by using the Kaplan Method.

Know How to Eliminate Data Sufficiency Answer Choices

As you’ve already learned, the directions and answer choices for Data Sufficiency questions never change, so it’s to your advantage to memorize them. But you can take this approach one step further by learning how to eliminate answer choices as you work through Data Sufficiency problems.

As you evaluate the two statements, use your noteboard to keep track of which answer choices you have ruled out as incorrect. Use the following patterns to guide your elimination:

If Statement (1) is sufficient, the answer could only be (A) or (D). Eliminate (B), (C), and (E).

If Statement (1) is insufficient, the answer could only be (B), (C), or (E). Eliminate (A) and (D).

If Statement (2) is sufficient, the answer could only be (B) or (D). Eliminate (A), (C), and (E).

If Statement (2) is insufficient, the answer could only be (A), (C), or (E). Eliminate (B) and (D).

Using the mnemonic device 12TEN will help you keep track of these answer choices, allowing you to attack the question more efficiently and avoid considering an answer choice you’ve already ruled out.

You also want to avoid a common mistake on Data Sufficiency: choosing (C) when the answer is actually (A), (B), or (D). Remember: if either statement by itself is sufficient, then of course the two statements together will also be sufficient, since the statements are always true and never contradict each other. But (C) can be correct only when each statement alone is insufficient and combining the statements is necessary to obtain sufficiency.

You should consider the statements together only if each is insufficient on its own. When you evaluate the statements together, keep in mind that each statement is true. So if you’re Picking Numbers to evaluate the statements combined, you must choose values that are permitted by both statements.

Know the Two Types of Data Sufficiency Questions

There are two broad types of Data Sufficiency questions, and they play by slightly different rules. The two types are Value questions and Yes/No questions. During Step 1 of the Kaplan Method for Data Sufficiency, you need to determine which type of question you’re dealing with, since this will determine your approach.

Value Questions

A Value question will ask you for the exact value of something. If a statement narrows the possibilities down to exactly one number, then it is sufficient. Otherwise, it is not. Of the Data Sufficiency questions you’ll see on Test Day, approximately two-thirds will be Value questions.

Let’s take a closer look at how this question type functions using a sample question:

Example:

What is the value of x?

(1)   x2 − 7x + 6 = 0

(2)   5x = 30

Step 1: Analyze the Question Stem

This is a Value question, meaning you need to find the value of x to obtain sufficiency. There’s nothing that needs to be simplified in this step, since there’s just one variable: x. Before you evaluate the statements, remember that sufficiency is obtained when you can identify one, and only one, possible value for x.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) can be reverse-FOILed to (x − 1)(x − 6) = 0, which means that there are two possible values for x, either 1 or 6. But you don’t even need to calculate these two values; once you know there is more than one possible value, you know that Statement (1) must be insufficient.

Statement (2) is a linear equation, containing a single variable. Therefore, there can only be one possible result (in this case, x = 6), and it is sufficient.

Since Statement (1) is insufficient and Statement (2) is sufficient by itself, the answer is (B).

Practice Set: Value Questions

Answers and explanations at end of chapter

  1. What is the value of 4n − 5m?

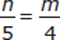
    • (1)   image

    • (2)   image

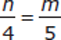
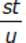  2. What is the value of image?

    • (1)   s = 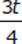image and u = 2t.

    • (2)   s = u − 10 and u = s + t + 2.

  3. If z is an integer, what is the units digit of z3?

    • (1)   z is a multiple of 5.

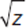    • (2)   image is an integer.

  4. What is the value of the integer p?

    • (1)   p is a prime number.

    • (2)   88 ≤ p ≤ 95

Yes/No Questions

Yes/No questions are, simply put, questions that call for a “yes” or a “no” answer. A key difference between Value questions and Yes/No questions is that a range of values can establish sufficiency for Yes/No questions. For example, if a question asks “Is x > 10?” a statement saying x < 9 will be sufficient.

Note that in this example, the answer to the question in the stem is, “No, x is never greater than 10.” Don’t confuse a “yes” to the question “Is Statement (1) sufficient?” with a “yes” to the question in the stem; they are not the same. This mistake is the most common pitfall test takers face on Yes/No questions. You can avoid this pitfall by remembering that any answer of “ALWAYS yes” or “ALWAYS no” is sufficient; only “sometimes yes, sometimes no” answers are insufficient. The definitiveness of your answer to the stem question is more important in determining sufficiency than whether the answer itself happens to be “yes” or “no.”

Sometimes Yes/No questions don’t appear to call for a “yes” or “no” answer. Suppose a Data Sufficiency question asks which employee, Jane or Sam, earned more in 2009. Ask yourself, “Do I absolutely need to know the specific values for Jane and Sam?” As it turns out, you don’t. You should handle this question the same way as you would a Yes/No question that asked, “Did Jane earn more than Sam last year?” In both cases you have sufficient information when you determine that only one answer is possible—Jane or Sam—even if you don’t know a precise value for either Jane’s earnings or Sam’s earnings. Again, you can determine sufficiency knowing only ranges of values (for example, it’s sufficient to know that Jane earned more than $20,000 and that Sam earned less than $16,000).

Let’s take a closer look at how this question type functions using a sample question:

Example:

If x is an integer, and 0 < x < 4, is x prime?

(1)   x > 1

(2)   x is even.

Step 1: Analyze the Question Stem

This is a Yes/No question, meaning you need to determine whether x is prime or not. According to the question stem, x could be 1, 2, or 3. You know that 2 and 3 are prime but 1 is not. In order to attain a definite “yes” answer, x must be either 2 or 3, and to obtain a definite “no” answer, x must be equal to 1. In other words, you could restate the question as “Does x equal 2 or 3?”

Step 2: Evaluate the Statements Using 12TEN

Start with Statement (1). Knowing that x is greater than 1 rules out 1, leaving only 2 and 3 as possible values of x. Since both 2 and 3 are prime, you have an answer: definitely “yes.” This statement is sufficient. Notice that you don’t know which of those two values x equals, but for a Yes/No question, knowing a precise value is irrelevant; you can still have sufficiency as long as you know the answer is “always yes” or “always no.” Eliminate choices (B), (C), and (E).

Now set aside Statement (1) and move on to Statement (2). Of the possible values of x—1, 2, and 3—only one of them is even. You’ve determined that x must be 2. Because 2 is prime, the statement gives you a definite “yes.” Statement (2) is also sufficient, so the answer is (D).

Practice Set: Yes/No Questions

Answers and explanations at end of chapter

  1. Is 4 + image an integer?

    • (1)   n is a multiple of 3.

    • (2)   n divided by 6 has a remainder of 0.

  2. If x and y are prime numbers, is y(x − 3) odd?

    • (1)   x > 10

    • (2)   y < 3

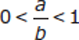  3. Is image?

    • (1)   ab > 1

    • (2)   a − b < 1

  4. If y > 0, is x less than 0?

    • (1)   xy = 16

    • (2)   x − y = 6

The Statements Are Always True

The statements are new pieces of data that apply to the problem and are always true. Don’t waste time trying to verify a statement.

The fact that the statements are always true has an important corollary that will help you catch careless errors: the statements will never contradict each other. Although they won’t always be sufficient to answer the question, they’ll never be mutually exclusive. If it appears that two statements are in disagreement with each other, you should recheck your work, because you have made an error.

Example:

What is the value of t?

(1)   t2 = t

(2)   t + 6 = 6

This is a straightforward Value question for which you need a value of t. Let’s say that you made an error in your analysis of Statement (1) and thought that t had to equal 1. You’d think that Statement (1) was sufficient.

Then you’d look at Statement (2). Simplifying, you’d learn that t equals 0. That’s also sufficient. So you’d think that the answer would be (D). However, according to your analysis, the statements contradict each other:

(1)   t = 1

(2)   t = 0

That isn’t possible. So you’d know to go back and recheck your work. Statement (2) pretty obviously says that t = 0, so you would recheck your work on Statement (1). Is 1 the only number that equals itself when squared? Substitute the 0 from Statement (2) and you get 02 = 0 × 0 = 0. So Statement (1) actually permits two values and is therefore insufficient.

(1)   t = 0 or 1

(2)   t = 0

The correct answer is (B), not (D).

It’s All About the Question Stem

On Data Sufficiency questions, if you rush past the question and dive into the statements, you risk doing a whole bunch of unnecessary—and possibly misleading—math. It’s essential that you understand the question stem before you analyze the statements. For one thing, there’s a huge difference between a Value question and a Yes/No question. Consider this identical pair of statements:

(1)   x3 = x

(1)   x3 = x

(2)   x2 = x

(2)   x2 = x

Here’s how they evaluate:

(1)   x = −1, 0, or 1

(1)   x = −1, 0, or 1

(2)   x = 0 or 1

(2)   x = 0 or 1

But you still have no idea what the answers are without seeing the question stems:

What is the value of x?

Is x < −1?

(1)   x = −1, 0, or 1

(1)   x = −1, 0, or 1

(2)   x = 0 or 1

(2)   x = 0 or 1

For the question on the left, a Value question, Statement (1) is insufficient because there are three possible values of x. Statement (2) is also insufficient because it permits two possible values. Even when the statements are considered together, x could be either 0 or 1. That’s two values, which is insufficient for a Value question. The answer is (E).

But the question on the right is a Yes/No question, so you will need to evaluate it differently. This question asks whether x is less than −1. First, look at Statement (1). Is −1 < −1? No. Is 0 < −1? No. Is 1 < −1? No. Always “no”: this statement is sufficient. The same for Statement (2): Both values answer the question with a “no,” so it’s sufficient, as well. The answer is (D).

That’s as different as two Data Sufficiency answers can be, and it had nothing to do with the statements, which were identical. It’s all about the question stem.

But during Step 1 of the Kaplan Method, you want to look for more than just whether the question is a Value or a Yes/No question. You saw how Problem Solving questions get much easier with some analysis and simplification before an approach is chosen. So too with Data Sufficiency.

Example:

If w ≠ x, w ≠ z, and x ≠ y>, is 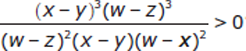image?

(1)   x > y

(2)   w > z

This is a Yes/No question that asks about a fraction containing multiple variable expressions as factors. At first glance, this may look like a scary question stem. But take a closer look at that fraction. There are a lot of shared terms in the numerator and the denominator. Using the laws of exponents, you can cancel the (w − z)2 and the (x − y) in the denominator:

If w ≠ x, w ≠ z, and x ≠ y, is 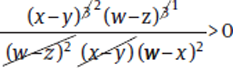image?

That simplifies the question to this:

If w ≠ x, w ≠ z, and x ≠ y, is 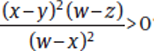image?

This is looking better already. You can simplify even further by thinking logically about the question. You aren’t asked for the value of anything, just whether this complicated fraction is positive. Without knowing anything about the values of w, x, y, and z, what can you already know about the answer to this question stem? Well, for one thing, you know that a squared term cannot be negative. So there’s no way that (x − y)2 or (w − x)2 is negative. In fact, since w ≠ x and x ≠ y, they can’t be zero, either. So those two terms are both positive, which is the only thing that matters to the question. You can simplify the question even further, to this:

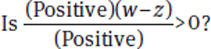
image

Since multiplying and/or dividing (w − z) by anything positive will not change its sign, you have this:

Is w − z > 0?

Now that’s a much simpler question. Look at how much easier the statements have become to evaluate:

(1)   x > y

(2)   w > z

Statement (1) is totally irrelevant to whether w − z > 0. This statement is insufficient.

Statement (2) tells you that w is bigger than z, so w − z must be positive. (Subtract z from both sides of the inequality, and you get w − z > 0.) That’s a definite “yes.” This is sufficient, so the answer is (B).

The more analysis and simplification you do with the question stem, the easier dealing with the statements will become.

Think About Sufficiency, Not Calculation

Get into the habit of thinking about what’s needed for sufficiency, rather than doing arithmetic calculations. One of the ways that the GMAT makes a Data Sufficiency question harder is to make the numbers scarier. But if you aren’t worrying about arithmetic, you won’t be fazed by this. Let’s take a look at two important math concepts that can help you avoid number crunching in Data Sufficiency.

The “N-Variables, N-Equations” Rule

Perhaps one of the most powerful tools to evaluate sufficiency is the n-variables, n-equations rule. If you have at least as many distinct, linear equations as you have variables, you will be able to solve for the unique numerical values of all the variables. If there are two variables, you need at least two equations to solve for all the values. If you have three variables, you need at least three equations. If you have four variables, you need at least four equations, and so on.

Note that when you apply the n-variables, n-equations rule, you must be alert to the exact definition of the word “distinct”: each equation must provide new, different information. For instance, even though the equations x + 3y = 5 and 2x + 6y = 10 look different, they are not in fact distinct—the second equation is merely the first equation multiplied by 2. Another example is the following system of equations: x + 2y − 3z = 8; 2y + 6z = 2; and x + 4y + 3z = 10. These may also initially seem to be distinct, but a closer look reveals that the third equation is merely the sum of the first two. It therefore adds no new information, so this system of equations cannot be solved for unique numerical values for each variable.

Example:

A souvenir shop made $2,400 in revenue selling postcards. If a large postcard costs twice as much as a small postcard, the shop sold 950 large postcards, and it sold no other type of postcard besides these two sizes, then how many small postcards did it sell?

(1)   A large postcard costs $2.

(2)   If the shop had sold 20% fewer small postcards, its revenue would have been reduced by 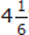image%.

There are four factors that affect the outcome of this problem: (1) the price of a small postcard, (2) the price of a large postcard, (3) the number of small postcards sold, and (4) the number of large postcards sold. That’s four variables, so four distinct, linear equations would enable you to solve for any of the variables. How many equations do you have already? Well, something-or-other equals $2,400 (that’s one), there’s a relationship between the prices (that’s two), and you get the number of large postcards (that’s three). With three equations for four variables, any new equation will be sufficient, as long as it is distinct and it doesn’t introduce a new variable.

Statement (1) is a new equation and is therefore sufficient. Statement (2) is a more complicated equation, and it would likely be time-consuming to calculate. But it is still a new, distinct equation, and it is therefore sufficient. The answer is (D).

Imagine how much time it would take to work through these equations. Using the n-variables, n-equations rule, it need take no longer than a minute.

One word of caution, though: having the same number of distinct, linear equations guarantees sufficiency, but having fewer does not guarantee insufficiency. The GMAT will set up equations so that you can sometimes solve for what’s asked even though you can’t solve for every variable individually.

Example:

A fruit stand sells apples, pears, and oranges. If oranges cost $0.50 each, then what is the cost of 5 oranges, 4 apples, and 3 pears?

(1)   The cost of 1 apple is $0.30.

(2)   The cost of 8 apples and 6 pears is $3.90.

There are three variables in this problem (the cost of an orange, the cost of an apple, and the cost of a pear), so three distinct equations could solve for everything. You’re given only one (the exact price of an orange). So two additional distinct equations will guarantee sufficiency. But you should keep your eyes open for a way to answer your question with fewer. Since you already know the price of an orange, the only thing you’d need to answer your question is the price of 4 apples and 3 pears.

Statement (1) is insufficient, as you still do not know anything about the price of a pear. Statement (2) is only one equation, but if you divided it by 2, you’d get the cost of 4 apples and 3 pears, which is exactly what you need. This statement is sufficient, so the correct answer is (B).

Proportions

Another common way that the GMAT allows you to get sufficiency without knowing all the individual values is to ask questions based on proportions (ratios, percents, averages, rates/speed, etc.). The goal of the following exercise is to get you to think about what kind of information can be sufficient to answer a question, even though you can’t calculate the exact value of every variable involved. Read the question stem and each of the following statements, asking yourself whether it gives you enough information to answer. Don’t waste time trying to come up with the actual value.

What was the percent increase in profits for Company X between 1991 and 1993?

Do the following statements provide sufficient information?

(1)   The company earned 20 percent less profit in 1991 than in 1993.

(2)   The average annual profit from 1991 to 1993 was 12.5% higher than the profit in 1991.

(3)   The average of the annual profits of 1991 and 1993 was 12.5% higher than the profit in 1991.

(4)   In 1991, the profit was $4.5 million less than in 1993.

Let’s evaluate each statement on its own:

Statement (1) is sufficient. You could “reverse” the math and figure out percent increase from the given decrease. Let the 1993 profit equal P1993 and the 1991 profit equal P1991. The statement can be translated to P1991 = 0.8 (P1993), which is P1991 = image(P1993). That means P1993 = imageP1991 = 1.25 (P1991). That’s 125% of 1991, or a 25% increase.

Statement (2) is insufficient because you don’t know anything about the profit in 1992, and this information would be necessary to set up the calculation.

Statement (3) is sufficient because you are given a proportional relationship between the two years’ profits: 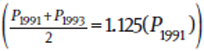image. The question asks you for a proportional relationship, so this is exactly what you need.

Statement (4) is insufficient because you aren’t given the total; you don’t know what percentage a $4.5 million difference represents.

TAKEAWAYS: THE BASIC PRINCIPLES OF DATA SUFFICIENCY

 

The basic principles of Data Sufficiency are the following:

DATA SUFFICIENCY STRATEGY

Now that you’re familiar with how Data Sufficiency questions are constructed, let’s look at two important strategic approaches to these questions. The first you’re already familiar with from the Problem Solving chapter: we’ll start by looking at how to effectively utilize the Picking Numbers strategy. After that, we’ll discuss in greater detail how to most effectively combine statements.

Picking Numbers in Data Sufficiency

You’ve already seen the power of the Kaplan strategy of Picking Numbers for Problem Solving questions. You can also use this strategy for many Data Sufficiency questions that contain variables, unknown quantities, or percents of an unknown whole. When using this strategy, you always pick at least two different sets of numbers, trying to prove that the statements are insufficient by producing two different results. It’s usually easier to prove insufficiency than sufficiency. But as you practice this strategy, the Core Competency of Pattern Recognition will also come into play. You will become adept at recognizing the types of numbers that can produce different results: positives vs. negatives, fractions vs. integers, odds vs. evens, and so on. Also, don’t hesitate to use the numbers 0 and 1, as they have unique properties that make them great candidates for the Picking Numbers strategy.

Applying the Kaplan Method: Picking Numbers in Data Sufficiency

Now let’s use the Kaplan Method on a Data Sufficiency question that involves Picking Numbers:

If a + b = 20, then what is the value of c − d?

(1)   ac − bd + bc − ad = 60

(2)   d = 4

Step 1: Analyze the Question Stem

Here’s a Value question, so you need one, and only one, value for the expression c − d. There’s nothing much to simplify here, but keep in mind that you are given a value for another expression, a + b. To obtain sufficiency, you’ll need values for both c and d or a way to relate the equation a + b = 20 to the expression c − d.

Step 2: Evaluate the Statements Using 12TEN

As always, think strategically. Since the GMAT doesn’t present the statements in any particular order, it’s sometimes wise to start by evaluating Statement (2) if it looks easier to evaluate than Statement (1). Here, Statement (2) gives you a value for d but not for c. There’s also no way to relate the equation a + b = 20 to the expression c − d. Eliminate (B) and (D). Notice that you’ve eliminated 50 percent of the wrong answer choices very quickly.

Now let’s tackle Statement (1), remembering to use the information it provides in conjunction with the question stem. You’re given a + b = 20, so let’s use Picking Numbers here. Pick a = 10 and b = 10.

Now, Statement (1) reads:

10c − 10d + 10c − 10d = 60

Combine the like terms:

20c − 20d = 60

Factor out the 20:

20(c −d) = 60

Divide out the 20:

c − d = 3

So, the expression c − d can equal 3. But you’re not finished yet. You have to pick a different set of numbers to see whether you can produce a different answer.

What permissible numbers might be likely to produce a different answer? Since Statement (1) involves subtraction, try negative numbers. Try a = 25 and b = − 5.

Now Statement (1) reads:

25c − (−5)d + (−5)c − 25d = 60

Move the common terms next to each other:

25c + (−5)c − (−5)d − 25d = 60

Simplify the positive and negative signs:

25c − 5c + 5d − 25d = 60

Combine like terms:

20c − 20d = 60

Factor out the 20:

20(c − d) = 60

Divide out the 20:

c − d = 3

After picking two sets of numbers that have different properties and receiving the same result, you can say with reasonable confidence that Statement (1) is sufficient. Eliminate (C) and (E). The correct answer is (A).

TAKEAWAYS: PICKING NUMBERS IN DATA SUFFICIENCY

 

Practice Set: Picking Numbers in Data Sufficiency

Answers and explanations at end of chapter

  1. If x is an integer with n distinct prime factors, is n greater than or equal to 3?

    • (1)   x is divisible by 6.

    • (2)   x is divisible by 10.

  2. If x3 < x, is x > x2?

    • (1)   x > −5

    • (2)   x < −2

  3. Is |15 − m| + |m − 15| > 15?

    • (1)   m > 6

    • (2)   m < 7

Combining Statements

If—and only if—each statement on its own is insufficient, you must then consider the statements together. The best way to do this is to think of the statements as one long sentence. At this stage, you can essentially approach the question as you would a Problem Solving question, using all the information you’re given to answer the question. The main difference is that, since this is still Data Sufficiency, you will stop solving as soon as you know that you can solve. The time saved by avoiding unnecessary calculations is better spent on questions later in the section.

As you’ve learned earlier in this chapter, information is always consistent between the statements. The statements never contradict each other. For example, you’ll never see a question in which Statement (1) says that x must be negative and Statement (2) says that x is positive. You might, however, learn from Statement (1) that x is greater than −5 and learn from Statement (2) that it’s positive. Learning to recognize how one statement does or does not limit the information in the other is the key in deciding between choices (C) and (E).

Combining Statements Exercise

Answers follow the exercises.

The following exercise contains a single question stem—“What is the value of x?”— and many sets of sample statements, which have already been simplified and evaluated for you. Imagine that you had analyzed the statements and gotten the possible values for x listed below: Which statements, either separately or combined, are sufficient to answer the question? Choose the appropriate Data Sufficiency answer choice—(A), (B), (C), (D), or (E)—for each pair of statements.

What is the value of x?

  1. (1)   x = −1, 0, 1

    (2)   x = 0, 1

  2. (1)   x < 3

    (2)   x > 3

  3. (1)   x = −1, 0

    (2)   x < 0

  4. (1)   x = −1, 1

    (2)   x = 1, 2

  5. (1)   x < 4

    (2)   x < 2

  6. (1)   x = −1, 0

    (2)   x = −1, 0

  7. (1)   x = −1, 1

    (2)   x = −1

  8. (1)   x ≥ 2

    (2)   x ≤ 2

  9. (1)   x is even.

    (2)   x is prime.

Combining Statements Exercise: Answers

  1. (E); x could be 0 or 1.

  2. (E); x could be any number between (but not including) 1 and 3. Don’t assume that variables are integers.

  3. (C); x = −1.

  4. (C); x = 1.

  5. (E); x could be any number smaller than 2.

  6. (E); x could be 0 or −1. Statements that give redundant information are never sufficient when combined.

  7. (B); Statement (2) is sufficient. Note that you would never combine statements in this case.

  8. (C); x = 2.

  9. (C); x = 2.

Applying the Kaplan Method: Combining Statements

Now let’s use the Kaplan Method on a Data Sufficiency question that involves Picking Numbers:

If x and y are positive integers, is 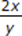image an integer?

(1)   Some factors of y are also factors of x.

(2)   All distinct prime factors of y are also prime factors of x.

Step 1: Analyze the Question Stem

First, this is a Yes/No question. Any statement that gives you a “sometimes yes; sometimes no” answer is insufficient. Now, how can you paraphrase the question in the stem? You can say either, “Is 2x a multiple of y?” or “Does 2x divide evenly by y?”

Step 2: Evaluate the Statements Using 12TEN

Use the Kaplan strategy of Picking Numbers. Pick permissible, manageable numbers. If you pick x = 5 and y = 5, that will give you a “yes” to the original question, since 2x, or 10, divided by y, or 5, will yield an integer. But if you pick a different set of numbers, say x = 2 and y = 42, that will yield a fraction. Statement (1) is insufficient; eliminate (A) and (D).

Pick numbers for Statement (2), making sure they’re permissible. For example, 36 and 6 have the same distinct prime factors: 2 and 3. Picking the numbers x = 36 and y = 6 gives you an integer; choosing x = 6 and y = 36, on the other hand, gives you a fraction. Therefore, Statement (2) is insufficient; eliminate (B).

Now, combining the statements, you will notice something interesting. Statement (2) is more restrictive than Statement (1). So as you combine the statements, ask yourself, “Will any numbers that satisfy Statement (2) also satisfy Statement (1)?” Yes, they will. For instance, x = 36 and y = 6, which you picked for Statement (2), also works for Statement (1): these numbers will again yield a “yes” answer. And x = 6 and y = 36 also works for Statement (1), yielding a “no” answer. Since combining the statements didn’t add any new information and the information presented was insufficient, the answer must be (E). Even combined, you get a “sometimes yes, sometimes no” answer to the question in the stem.

TAKEAWAYS: COMBINING STATEMENTS

 

Practice Set: Combining Statements

Answers and explanations at end of chapter

  1. What is the value of x?

    • (1)   x2 − 9 = 16

    • (2)   3x(x − 5) = 0

  2. Is y2 < 1?

    • (1)   y > −1

    • (2)   y < 1

  3. If a coffee shop sold 600 cups of coffee, some of which were large cups and the remainder of which were small cups, what was the revenue that the coffee shop earned from the sale of coffee?

(1)   The number of large cups sold was image the total number of small cups sold.

(2)   The price of a small cup of coffee was $1.50.

Answer Key

Practice Set: The Kaplan Method for Data Sufficiency

  1. B

  2. D

  3. C

  4. A

  5. E

Practice Set: Value Questions

  1. A

  2. C

  3. E

  4. C

Practice Set: Yes/No Questions

  1. B

  2. D

  3. E

  4. D

Practice Set: Picking Numbers in Data Sufficiency

  1. C

  2. B

  3. B

Practice Set: Combining Statements

  1. C

  2. C

  3. E

Answers and Explanations

Practice Set: The Kaplan Method for Data Sufficiency

1.    (B)

If x > 0, what is the value of x?

(1)   x > 5

(2)   40 − x2 = 4

Step 1: Analyze the Question Stem

In this Value question, sufficiency means finding one and only one value for x. We are told that x must be greater than 0.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that x > 5. While that certainly narrows down the options for x, there is no way to figure out one and only one value for x from that information alone, so this statement is insufficient. Eliminate (A) and (D).

Statement (2) provides an equation that allows us to determine the value of x2. Every positive number has two square roots, one positive and one negative, so this statement narrows the options down to two values for x. This would normally not be sufficient. However, the question stem states that x > 0, which eliminates the negative square root, leaving one and only one value for x. Statement (2) alone is sufficient, so (B) is correct.

2.    (D)

If a > 0, b > 0, and 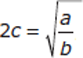image what is the value of b?

(1)   a = 8 and c = 2

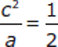
(2)   image

Step 1: Analyze the Question Stem

In this Value question, sufficiency means finding one and only one value for b. We are told that a and b are both positive and are given an equation. Let’s simplify the equation before proceeding to the statements.

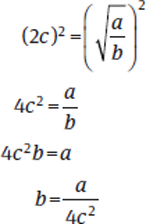
image

Solving for b means having either the values for both a and c or the value of 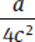image.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) provides the values of a and c. By plugging these provided values into the expression 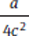image, we can solve for b, so Statement (1) is sufficient. Eliminate (B), (C), and (E).

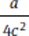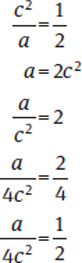
Statement (2) may not look sufficient at first glance, but we can actually change the left side of the equation to image:

image

Since 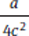image is also the value of b, this statement is sufficient. Eliminate (A).

Each statement alone is sufficient to answer the question, so (D) is the correct answer.

3.    (C)

Team X won 40 basketball games. What percent of its basketball games did Team X win?

(1)   Team X played the same number of basketball games as Team Y.

(2)   Team Y won 45 games, representing 2.5 percent of the basketball games it played.

Step 1: Analyze the Question Stem

In this Value question, the stem gives us the number of games won by Team X and asks for the percentage of games the team won. For sufficiency, we need to be able to determine the number of games Team X played. From that, we can determine Team X’s winning percentage.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that Team X played the same number of games as Team Y, but we know nothing of Team Y. This statement is insufficient, so we can eliminate (A) and (D).

Statement (2) tells us how many games Team Y won and gives us enough information to calculate how many total games Team Y played. Because we do not know the relevance of Team Y’s performance from this statement (remember not to combine the statements yet), the statement is insufficient. We can eliminate (B).

Because each of the statements is insufficient alone, we now combine the statements. From Statement (2), we could determine the number of games that Team Y played, and from Statement (1), we know that this is equal to the number of games that Team X played. Together, the statements are sufficient, so the correct answer choice is (C).

4.    (A)

If 2b − a2 = 18, what is the value of b?

(1)   a2 = 1,156

(2)   a > 0

Step 1: Analyze the Question Stem

This is a Value question, which means that sufficiency requires one and only one value for b. We need a value for a or a2 in order to solve for b.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) gives a value for a2. Therefore, it is sufficient, thus eliminating (B), (C), and (E).

Statement (2) gives a range of values for a. This is insufficient, eliminating (D).

Therefore, the correct answer is (A); Statement (1) alone is sufficient.

Note that using the Kaplan Method will keep you from falling into a trap laid by the testmaker. If you thought from the first statement that having two possible values—one positive and one negative—for a meant that the information was insufficient to get one value, you might have thought you needed the information in Statement (2) to get one value for a. However, by determining what you need for sufficiency before looking at the statements, you realized that it does not matter whether we have the positive or negative value of a, as long as we can solve for one and only one value for b.

5.    (E)

A certain company produces exactly three products: X, Y, and Z. In 1990, what was the total income for the company from the sale of its products?

(1)   In 1990, the company sold 8,000 units of product X, 10,000 units of product Y, and 16,000 units of product Z.

(2)   In 1990, the company charged $28 per unit for product x and twice as much for product Z.

Step 1: Analyze the Question Stem

In this Value question, we are told that a company makes three products and are asked to find the total income from the sale of these products. For sufficiency, we need to be able to determine the quantities and prices of all three products.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) gives us quantity information, by product, for each of the three products. Because it has no pricing information, the statement is insufficient. Eliminate (A) and (D).

Statement (2) gives us pricing information for one product and information to calculate the price of a second product. However, it has no quantity information and nothing about the pricing of the third product. The statement is therefore insufficient, and you can eliminate (B).

Because each of the statements is insufficient, we now combine the statements. When combined, we have quantity information for all three products but only have pricing information for two of them. Therefore, the two statements combined are insufficient to answer the question. Answer choice (E) is correct.

Practice Set: Value Questions

6.    (A)

What is the value of 4n − 5m?

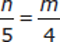
(1)   image

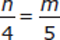
(2)   image

Step 1: Analyze the Question Stem

This Value question requires one and only one value for the expression 4n − 5m. We will either need to find the value for that expression or find the values of n and m individually.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) may not look like much help at first, but cross multiplying results in the equation 4n = 5m. Subtract 5m from both sides to find that 4n − 5m = 0. This is one and only one value for the expression in the question stem, so this statement is sufficient. Eliminate (B), (C), and (E).

Statement (2) looks very similar to Statement (1), but cross multiplying here results in the equation 5n = 4m. From this, there is no way to figure out the values of n or m (we would need two distinct equations to do that, given that there are two variables) and no way to isolate 4n − 5m. Statement (2) is therefore insufficient, so we can eliminate (D).

Statement (1) alone is sufficient, so the correct answer is (A).

7.    (C)

What is the value of 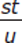image?

(1) 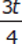  image and u = 2t.

(2)   s = u − 10 and u = s + t + 2.

Step 1: Analyze the Question Stem

This is a Value question. The stem for this item includes three variables. Specific values for each of the variables would be sufficient to get one value for the entire expression.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) gives us restatements of two of the variables—s and u—in terms of the third variable, t. If we take the expression in the stem and replace s and u with the expressions given in the statement, we can see that the variable t is not eliminated:

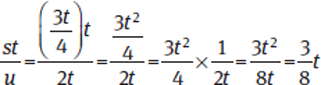
image

Therefore, Statement (1) is insufficient, and we can eliminate (A) and (D).

At first glance, Statement (2) appears to invite a similar conclusion to the one for Statement (1). However, further analysis of the information is worth a try. We are told that s = u − 10 and also that u = s + t + 2. Substituting u − 10 for s in the second equation, we find that

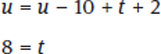
image

Substituting the value of 8 for t and substituting u −10 for s,

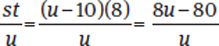
image

Unfortunately, this still doesn’t eliminate the variable u, so Statement (2) is insufficient and we can further eliminate (B).

Combining the statements, we determined from Statement (1) that the expression 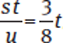image. If we substitute the value of 8 for the variable t—from Statement (2)—we see that we can get one value even without actually solving the math.

Therefore, the correct answer is (C): Neither statement alone is sufficient, but the statements combined are sufficient.

8.    (E)

If z is an integer, what is the units digit of z3?

(1)   z is a multiple of 5.

(2) 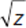  image is an integer.

Step 1: Analyze the Question Stem

In this Value question, to have sufficiency, we need to know either the value of integer z or something about z that would enable us to determine the units digit of its cube.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that z is a multiple of 5. Multiples of 5 have units digits of either 0 or 5. Cubes of numbers with units digits of 0 or 5 keep the same units digit (e.g., the cube of 10 is 1,000; the cube of 5 is 125). The statement is insufficient because it gives us two possible answers to the question stem. Eliminate (A) and (D).

Statement (2) tells us that the square root of z is an integer. This means that z is a perfect square. The statement is insufficient because there are perfect squares with many different units values. Eliminate (B).

Because each of the statements is insufficient on its own, we now combine the statements. Combined, we know that z is both a multiple of 5 and a perfect square. If we can find examples for z that are perfect squares ending in each of the values from Statement (1), then the combined statements are insufficient. If z = 25, it is a multiple of 5 and its square root is an integer, and the answer to the question stem is 5. If z = 100, then both statements are true, and the answer to the question is 0. Since more than one answer to the question is possible, the two statements taken together are insufficient. Eliminate (C). (E) is the correct answer.

9.    (C)

What is the value of the integer p?

(1)   p is a prime number.

(2)   88 ≤ p ≤ 95

Step 1: Analyze the Question Stem

This is a Value question, so we’ll need one exact value for p. There’s nothing to simplify in the question stem, but it’s worth noting that p is an integer—we won’t need to consider decimal values. So what we need is very clear—one specific numeric value for p.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) doesn’t give us one exact value, as there are many prime numbers. Eliminate (A) and (D).

Likewise, Statement (2) doesn’t give us one exact value, only a range with eight possibilities. Eliminate (B).

To choose between (C) and (E), we must consider these statements in combination. Treating (1) and (2) as one long statement, we know that p is between 88 and 95, inclusive, and that it’s prime. If you happen to have all the primes through 100 memorized, then you know right away that p can only equal 89 and that the answer is (C).

But what if you don’t have all those primes memorized? When evaluating a reasonably short list of numbers, it’s often beneficial to write out the possibilities on your noteboard. Then, instead of the abstract “88 ≤ p ≤ 95,” we have p = 88, 89, 90, 91, 92, 93, 94, or 95. A prime number is a number that is divisible only by 1 and itself. So any of these that are divisible by any other number can be crossed off the list. If we can cross off seven of these eight numbers, we’ll know p.

Any even number is divisible by 2, so that eliminates 88, 90, 92, and 94. Any number that ends in a 0 or a 5 is divisible by 5, so that eliminates 95 (and 90, if it weren’t already gone). We know that 93 is divisible by 3. (The divisibility test for 3 is to check whether the digits of a number sum to a multiple of 3; if so, that number is itself divisible by 3. The digits of 93 are 9 and 3. Since 9 + 3 = 12 and 12 is a multiple of 3, 93 is a multiple of 3.)

Now we’ve narrowed the possibilities down to p = 89 or 91. We’ve checked for divisibility by the primes 2, 3, and 5. What about the next prime, 7? There is a little-known way to test divisibility by 7. But the GMAT often rewards test takers who think about numbers in creative ways, so even if you don’t know the divisibility rule, you can still try to break 91 into multiples of 7 that you know. Because 91 is also 70 + 21, it’s 7(10) + 7(3), or 7(10 + 3), or 7(13). So, it’s definitely a multiple of 7 and can be eliminated. We have now determined that p must equal 89. The statements together are sufficient, so the answer is (C).

(Incidentally, that little-known divisibility test for 7 is this: separate the units digit from the rest of the number, then multiply that units digit by 2. Subtract that from what’s left of the original number. If the result is a multiple of 7, the original number is a multiple of 7. Here’s how that works for 91. Separate 91 into the digits 9 and 1. Multiply 1 by 2: 1 × 2 = 2. Subtract: 9 − 2 = 7. 7 is obviously a multiple of 7, so 91 is a multiple of 7. Try it out on other multiples of 7, and you’ll see that it works every time.)

Practice Set: Yes/No Questions

10.   (B)

Is 4 + image an integer?

(1)   n is a multiple of 3.

(2)   n divided by 6 has a remainder of 0.

Step 1: Analyze the Question Stem

This Yes/No question asks whether 4 + image is an integer. Sufficiency means showing that the value of the expression is definitely an integer or definitely not an integer. As 4 is an integer and will therefore have no effect on whether the entire expression is equal to an integer, we simply need to consider whether image is definitely an integer.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) narrows the value of n to multiples of 3. Picking Numbers can illustrate for us: if n = 6, image is an integer, but if n = 9, image is not an integer. There is no definite “yes” or “no” outcome for the given expression, so this statement is insufficient. Eliminate (A) and (D).

Statement (2) restricts n to values that leave a remainder of 0 when divided by 6. These are, by definition, multiples of 6, and any multiple of 6 for n will always make image an integer. This statement provides a definite “yes” answer, so it is sufficient. Eliminate (C) and (E).

Statement (2) alone is sufficient, so the correct answer is (B).

11.   (D)

If x and y are prime numbers, is y(x − 3) odd?

(1)   x > 10

(2)   y < 3

Step 1: Analyze the Question Stem

This is a Yes/No question. We are asked whether a particular expression is odd. For sufficiency, we need to be able to determine whether the solution to the expression is definitely odd or definitely even. Here, we should consider the rules of odds and evens: (odd × odd) = odd, (even × even) = even, and (odd × even) = even; (odd + odd) = even, (odd + even) = odd, and (even + even) = even. So if either y is even or if x is odd (making x − 3 even), we will be able to answer the question with a “no.” Note also that we’re told that x and y are prime numbers. Seeing that we’re asked about odd numbers, and seeing that we’re dealing with primes, we should expect that the question involves the fact that 2 is the only even prime number.

Step 2: Evaluate the Statements Using 12TEN

Statement (1): If x is a prime number greater than 10, then it must be odd. Therefore, x − 3 must be even. The statement is sufficient to answer the question stem with a “no,” which eliminates (B), (C), and (E).

Statement (2): If y is a prime number less than 3, y must equal 2, which is even. The statement is sufficient to answer the question stem with a “no.” That eliminates (A) and tells us that (D) is the correct answer.

Because at least one of the statements alone is sufficient to answer the question, we do not evaluate the statements combined.

12.   (E)

Is 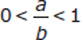image?

(1)   ab > 1

(2)   a − b < 1

Step 1: Analyze the Question Stem

This is a Yes/No question. For sufficiency, a definite “yes” would show that image is always a positive fraction less than 1, or a definite “no” would show that image is always something other than a positive fraction less than 1. Picking Numbers will help simplify this.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that ab is greater than 1. That means either that a and b are both positive or that they are both negative. Let’s pick some numbers to test out the possibilities:

Case 1:

a = −3, b = −2

(−3)(−2) > 1

Stem question: No

Case 2:

a = 2, b = 3

(2)(3) > 1

Stem question: Yes

Because we can pick numbers that follow the rules of the statement without giving a clear “yes” or “no” answer to the question stem, the statement is insufficient. We can eliminate (A) and (D).

Statement (2) tells us that a − b is less than 1. The same pairs of numbers we tested for Statement (1) apply here as well, making the statement insufficient.

Case 1:

a = −3, b = −2

(−3) − (−2) < 1

Stem question: No

Case 2:

a = 2, b = 3

2 − 3 < 1

Stem question: Yes

We can eliminate (B).

Because each of the statements is insufficient on its own, we now combine the statements. Since the same cases applied to both statements, combining the statements adds no new information to the analysis, and the combined statements are therefore insufficient. The answer must be (E).

13.   (D)

If y > 0, is x less than 0?

(1)   xy = 16

(2)   x − y = 6

Step 1: Analyze the Question Stem

This is a Yes/No question. What can we learn from the stem? It tells us that y is positive and asks us whether x is negative. What would constitute sufficiency? Learning that x is definitely negative or that x is definitely not negative. (Keep in mind that the number 0 is neither positive nor negative.)

Step 2: Evaluate the Statements Using 12TEN

Statement (1) tells us that xy = 16. To get a positive outcome when multiplying two variables, we need to have either two positive numbers or two negative numbers. Because the question stem tells us that y is positive, that means that x also has to be positive. Therefore, this statement is sufficient to answer the question with a “no” (x cannot be negative in this case), and we can eliminate (B), (C), and (E).

Statement (2) tells us that x − y = 6. Adding y to both sides of this equation shows that x is 6 greater than y. Since we already know that y is positive, Statement (2) is sufficient to answer the question with a “no,” and we can eliminate (A).

The correct answer is (D): Either statement alone is sufficient to answer the question.

Practice Set: Picking Numbers in Data Sufficiency

14.   (C)

If x is an integer with n distinct prime factors, is n greater than or equal to 3?

(1)   x is divisible by 6.

(2)   x is divisible by 10.

Step 1: Analyze the Question Stem

This is a Yes/No question, so we don’t need to know the exact value of n, just whether n ≥ 3.

There’s nothing to simplify, but it’s important to note the relationship between the variables: n is the number of distinct prime factors of x. (Every non-prime number can be rewritten as a series of prime numbers multiplied together; those are the number’s prime factors.)

To answer the question, we’ll need to know whether or not x has at least three distinct prime factors.

Step 2: Evaluate the Statements Using 12TEN

Let’s say that you weren’t sure how to evaluate the statements abstractly. Picking Numbers allows you to evaluate a Data Sufficiency statement when you aren’t comfortable with a more rules-based approach.

Statement (1): Let’s pick the simplest number that’s divisible by 6, namely x = 6 itself. We get 6 = 2 × 3. Since there are two prime factors, n = 2. Now test that number in the question: “Is 2 ≥ 3?” No, it isn’t.

But our work on Statement (1) isn’t done. We only know that Statement (1) can yield the answer “no.” We have no idea yet whether the answer is “definitely no,” because other permissible numbers might yield different results. Always test at least two sets of numbers when Picking Numbers in Data Sufficiency so that you can differentiate between the definite answers and the maybe answers.

Since we already got a “no” answer, our task is to see whether we can get a “yes,” thus proving that Statement (1) does not provide one definite answer. Could we think of a value for x that has three or more prime factors? Since 2 and 3 showed up as prime factors already, we can think of a value for x that has a different prime factor: 5, perhaps. So let’s pick x to be a multiple of 5 that is also divisible by 6 (otherwise it won’t be permissible). x = 30 fits the bill: 30 = 2 × 3 × 5. That’s three prime factors, so n = 3. Put that into the question: “Is 3 ≥ 3?” Yes, it is.

Because we’ve found both a “yes” and a “no” answer, Statement (1) answers the question “maybe yes, maybe no.” That’s not a definite answer, so Statement (1) is insufficient. Eliminate (A) and (D).

Statement (2): Now let’s pick the simplest number that’s divisible by 10, namely x = 10 itself. We get 10 = 2 × 5. Since there are two prime factors, n = 2. Now test that number in the question: “Is 2 ≥ 3?” No, it isn’t. Let’s see whether we can pick a number that yields a different answer. We’ve already seen a number that has three prime factors: 30. And it’s divisible by 10, so it’s permitted by Statement (2). We get 30 = 2 × 3 × 5. That’s three prime factors, so n = 3. Put that into the question: “Is 3 ≥ 3?” Yes, it is. As with Statement (1), we’ve produced a “maybe” answer, so Statement (2) is insufficient. Eliminate (B).

(C) and (E) still remain, so now we have to consider the statements together. We have to pick values for x that are divisible both by 6 and by 10. Happily, we already know one from our earlier work. If x = 30, then the answer to our question is “yes.” Can we find a number that’s divisible both by 6 and by 10 but has fewer than three prime factors? Let’s try x = 6 × 10, or x = 60. We get 60 = 6 × 10 = 2 × 3 × 2 × 5 = 22 × 3 × 5. That’s also three distinct prime factors. If you weren’t at this point confident that any number that’s divisible both by 6 and by 10 would have to have 2, 3, and 5 as prime factors (that’s at least three!), quickly testing one or two other possibilities (e.g., x = 90, x = 120) would confirm it. No matter what permissible numbers we pick, we get the same answer: “yes.” So considering the statements together, the answer is “definitely yes.” (C) is correct.

15.   (B)

If x3 < x, is x > x2?

(1)   x > −5

(2)   x < −2

Step 1: Analyze the Question Stem

This is a Yes/No question, so we don’t need to know the exact value of x, just whether x is definitely greater than x2 or definitely not greater than x2.

Is it possible to simplify the question? We’re told that x3 < x. When would a number be greater than its cube? Picking Numbers can help us understand the question. If x = 2, then x3 = 8; 8 is not less than 2, so x = 2 is not a permissible number according to the question stem. Neither is x = 1 nor x = 0, as in both cases x3 = x. What about other kinds of numbers, like fractions or negatives?

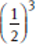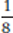If x = image, then x3 = image = image. Because 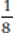image is less than 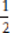image, x could be a fraction between 0 and 1. And if x = −2, then x3 = −8; −8 is less than −2, so x could be a negative number less than −1.

How would these different possible values affect the question “Is x > x2”? If x = 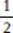image, then x2 = 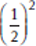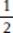image = image; image is greater than image. So if x is a fraction between 0 and 1, the answer to the question is “yes.” And if x = −2, then x2 = 4; −2 is not greater than 4, so if x is negative, then the answer to our question is “no.”

To answer the question, we’ll need to know definitely which of the two permitted types of number x is—a positive fraction or a number less than −1.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) permits any number greater than −5. Certainly x could be negative. And since there’s no upper limit provided on x, it could also be a positive fraction. We haven’t gotten a definite “yes” or “no” answer to our question, so Statement (1) is insufficient. Eliminate (A) and (D).

Statement (2) permits only negative numbers and excludes positive fractions. So the answer to our question is “definitely no.” Statement (2) is sufficient, so (B) is correct.

16.   (B)

Is |15 − m| + |m − 15| > 15?

(1)   m > 6

(2)   m < 7

Step 1: Analyze the Question Stem

In this Yes/No question, sufficiency means proving that |15 − m| + |m − 15| is either definitely greater than 15 or definitely less than or equal to 15. As the question stem is dealing with a range, Picking Numbers will help in evaluating the statements.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) restricts m to values greater than 6. When Picking Numbers to evaluate statements, remember to always pick at least two sets of numbers to see if you can get more than one possible answer to the question—in this case, let’s pick one number near the start of the range and one much farther away. Let’s first try m = 7.

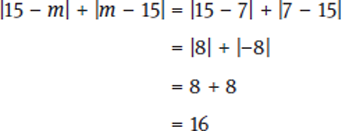
image

Since 16 is greater than 15, m = 7 results in a “yes” answer to the question. Let’s now try m = 15.

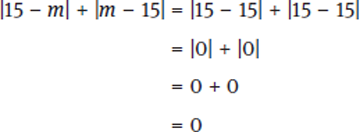
image

Since 0 is less than 15, m = 15 results in a “no.” As m > 6 sometimes means “yes” and sometimes means “no,” this statement is insufficient. Eliminate (A) and (D).

Statement (2) restricts m to values less than 7. We’ll need to pick at least two values once again, so let’s start with m = 6.

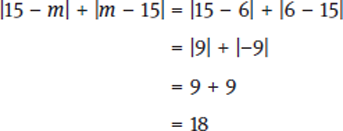
image

Because 18 is greater than 15, that’s a “yes.” Let’s try m = 0.

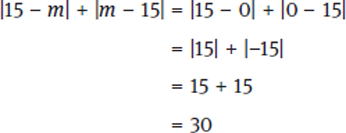
image

Not only is that also a “yes,” but the value is actually getting larger as m gets smaller, so this statement will always return an answer of “yes” to the question. Eliminate (C) and (E).

Statement (2) alone is sufficient, so the correct answer is (B).

Practice Set: Combining Statements

17.   (C)

What is the value of x?

(1)   x2 − 9 = 16

(2)   3x(x − 5) = 0

Step 1: Analyze the Question Stem

In this Value question, we must find one and only one value for x to have sufficiency.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) provides an equation that allows us to determine the value of x2. Every positive number has two square roots, one positive and one negative, so this statement narrows things down to two values for x: 5 and −5. Without further information, we cannot determine one and only one value for x, so this statement is insufficient. Eliminate (A) and (D).

Statement (2) provides an equation in which at least one of the expressions 3x or (x − 5) is equal to 0. That translates into two possible values for x: 0 and 5. We need one and only one value for sufficiency, so this statement is insufficient. Eliminate (B).

Combining the statements tells us that x is either 5 or −5 and either 0 or 5. The only way to satisfy both statements is for x to be 5. That is the one and only one possible value for x, so combining the statements leads to sufficiency, and the correct answer is (C).

18.   (C)

Is y2 < 1?

(1)   y > −1

(2)   y < 1

Step 1: Analyze the Question Stem

In this Yes/No question, sufficiency means determining that y2 is either definitely less than 1 or definitely greater than or equal to 1. All squares are non-negative—so how could it be that y2 is less than 1? The only way this could happen is if y fell somewhere between 1 and −1 on the number line. The square of 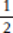image, for instance, is image; the square of −image is also image. Likewise, the square of 0 is 0. So the question stem can be simplified to “Is y less than 1 and greater than −1?”

Step 2: Evaluate the Statements Using 12TEN

Statement (1) states that y > −1. Picking Numbers will make this easier: y = 0 leads to a “yes” answer, as y2 would be less than 1. However, y = 2 leads to a “no” answer, as y2 would be greater than 1. This statement is insufficient, so we can eliminate (A) and (D).

Statement (2) states that y < 1. As we saw above, y = 0 leads to a “yes” answer. However, y = −2 would lead to a “no” answer, as y2 would be greater than 1. This statement is insufficient, so we can eliminate (B).

Combining the statements results in the inequality −1 < y < 1. That effectively limits the range of values for y to 0 and fractions whose absolute value is less than 1. Squaring any fraction whose absolute value is less than 1 will always result in a positive fraction less than 1, which produces a “yes” answer, and we’ve already seen that y = 0 produces a “yes” answer. Therefore, combining the statements will produce a definite “yes” to the question and the correct answer is (C).

19.   (E)

If a coffee shop sold 600 cups of coffee, some of which were large cups and the remainder of which were small cups, what was the revenue that the coffee shop earned from the sale of coffee?

(1)   The number of large cups sold was image the total number of small cups sold.

(2)   The price of a small cup of coffee was $1.50.

Step 1: Analyze the Question Stem

This is a Value question. Simplifying a word problem essentially entails understanding the situation, allowing us to figure out what variables would need to be calculated in order to answer the question. This coffee shop sells two sizes of coffee, and we are asked to determine its revenue. To answer this question, we need to ascertain both how many cups of each size were sold and the price of each size of cup.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) has no pricing information at all. We can eliminate (A) and (D) as potential answers. Even though we could create an equation that, when combined with the stimulus, would tell us the number of cups of each size that were sold, doing so would be a waste of time—we already know that Statement (1) is insufficient, so there’s no point in working further.

Statement (2) tells us the price of one size—small. This is insufficient because it tells us nothing about the price of the large cup or about the number of cups sold. We can now eliminate (B).

Because each statement alone is insufficient, we now combine both statements to determine whether they are sufficient together. Combined, we still know nothing about the price of a large cup. A crucial piece of data is missing, so the two statements combined are insufficient to answer the question. Eliminate (C). The correct answer is (E).

Strategic Guessing

When you run into a very complicated question, like the following, don’t forget to use a sound Data Sufficiency guessing strategy. That means perhaps skipping a statement that looks too daunting and trying to eliminate some answer choices by looking at the easier statement. Try your hand at the difficult question below. Don’t try to solve it; instead, see if you can narrow down the possibilities quickly.

Example:

What was the maximum temperature in City A on Saturday, May 14?

(1)   The average (arithmetic mean) of the maximum daily temperatures in City A from Sunday, May 8, to Saturday, May 14, was 72 degrees, which was 2 degrees less than the average (arithmetic mean) of the maximum daily temperatures in City A from Monday, May 9, to Friday, May 13.

(2)   The maximum temperature in City A on Saturday, May 14, was 5 degrees greater than the maximum temperature in City A on Sunday, May 8.

Step 1: Analyze the Question Stem

This is a Value question. To obtain sufficiency, you need an exact maximum temperature.

Step 2: Evaluate the Statements Using 12TEN

Statement (1) is long and complicated. Skip it and go straight to Statement (2); it’s much easier.

Statement (2) tells you that the value you’re looking for is 5 degrees more than the temperature on some other day. Without knowing the temperature on that other day, you don’t have the information you need. This statement is insufficient. You can eliminate (B) and (D) and give yourself a one-in-three chance to get the right answer without even evaluating Statement (1).

Perhaps you feel comfortable evaluating Statement (1). Perhaps you don’t. But let’s pretend for a moment that you aren’t sure how to evaluate Statement (1). Keep in mind that on the GMAT, complicated or hard-to-evaluate statements are more likely to be sufficient than insufficient. For this reason, you should avoid (E) and lean toward (A), unless you have a logical reason to suspect that Statement (1) alone is insufficient. Of course, this doesn’t guarantee you a correct answer, but if you’re falling behind on time, it will help you move through the Quantitative section most efficiently. Remember, no one particular question will make or break your GMAT score, but spending too much time on one question and having to rush through several others just to make up for the lost time will hurt your score. As it turns out, (C) is the right answer to this particular problem.

Fortunately, you’re unlikely to run into anything as complicated as Statement (1) on Test Day. The point of this exercise is to show you that even if you do encounter something this difficult, you’re still in control. If you work the odds and look for the strategic approach, you will increase your likelihood of picking up the points even for questions you’re not sure how to solve.

For the record, let’s analyze Statement (1). If the average maximum temperature from May 8 to May 14 was 72 degrees, then the sum of the maximum temperatures of those days is 7 × 72 = 504 degrees. If the average maximum temperature from May 9 to May 13 was 72 + 2, or 74 degrees, then the sum of the maximum temperatures of those days was 5 × 74 = 370 degrees.

The difference between those two sums is simply the sum of the maximum temperature on May 8, which you can call x, and the maximum temperature on May 14, which you can call y (since these two days were left out of the second time period). So x + y = 504 − 370 = 134. Statement (1) by itself is insufficient. But

Statement (2) tells you that y − x = 5. You have the two distinct linear equations, x + y = 134 and y − x = 5. These equations can be solved for a single value for y, so the statements taken together are sufficient: choice (C).

This example demonstrates how guessing can be a good alternative approach for certain questions. By looking at only one statement, you can narrow down the possibilities to two or three choices. This can be a great help, particularly on difficult or time-consuming problems for which you think you might have to guess. But you must be sure you know the rules for eliminating answer choices absolutely cold by Test Day.

GMAT BY THE NUMBERS: DATA SUFFICIENCY

Now that you’ve learned how to approach Data Sufficiency questions on the GMAT, let’s add one more dimension to your understanding of how they work.

Take a moment to try the following question. The next page features performance data from thousands of people who have studied with Kaplan over the decades. Through analyzing this data, we will show you how to approach questions like this one most effectively and how to avoid similarly tempting wrong answer choice types on Test Day.

image

In the figure above, a circle is inscribed in square ABCD. What is the area of ΔCDE?

(1)   The circle has a radius of length 3.

(2)   CDE is isosceles.

Explanation

You’re asked to find the area of triangle CDE. The area of a triangle is equal to image base × height. You can use CD as a base, and the height would be the length of a perpendicular drawn from point E to CD. Since that perpendicular line would be equal in length to BC, you only need to learn the length of the sides of square ABCD to know the length of both the base (CD) and the height (equal to BC) of triangle CDE.

Statement (1) says that the radius of the inscribed circle is 3, so you know that its diameter is 6. That diameter will equal the length of the sides of the square, which is what you need to answer the question. So Statement (1) is sufficient. Statement (2), however, gives you no measurements to work with at all. It does allow you to figure out that point E bisects AB, but that’s irrelevant to the question. Statement (2) is insufficient. Since Statement (1) is sufficient but Statement (2) is not, the correct answer is (A).

QUESTION STATISTICS
44% of test takers choose (A)
2% of test takers choose (B)
32% of test takers choose (C)
1% of test takers choose (D)
21% of test takers choose (E)
Sample size = 4,069

The question statistics reveal two very common habits that lead to wrong answers. Many test takers select (C), believing that the statements are sufficient only when combined. Statement (1) alone does not tell you the exact placement of point E. But you don’t need that information to know the triangle’s height, and therefore its area. You don’t always need to know everything to be able to answer the question that’s asked.

Also, some people struggle to relate the data about the circle to the square and then to the triangle. They look at Statement (1) and think, “I don’t know how to solve with this,” so they treat the statement as insufficient, leading in this question to choice (E). But to do so is to equate “I don’t know how to solve this” with “This can’t be solved”—not the same thing at all! You can see from the question statistics that this is a common line of thinking—and not one that the GMAT likes to reward. Be wary of guessing that a statement is insufficient unless you can see exactly why it doesn’t lead to a clear answer. If you don’t know how to deal with a statement, guessing that it’s sufficient is often the better strategy.

More GMAT by the Numbers …

To see more questions with answer choice statistics, be sure to review the full-length CATs in your online resources.