After parameter tuning, we can now run the model for maximum performance. In order to do so, we will make a few important changes to the model options. Ahead of making the changes, let's have a more in-depth review of the model options:
- hidden_node: These are the number of nodes in the hidden layer. We used a looping function to find the optimal number of nodes.
- out_node: These are the number of nodes in the output layer and must be set equal to the number of target classes. In this case, that number is 2.
- out_activation: This is the activation function to use for the output layer.
- num.round: This is the number of iterations we take to train our model. In the parameter tuning stage, we set this number low so that we could quickly loop through a number of options; to get maximum accuracy, we would allow the model to run for more rounds while at the same time dropping the learning rate, which we will cover soon.
- array.batch.size: This sets the batch size, which is the number of rows that are trained at the same time during each round. The higher this is set, the more memory will be required.
- learning.rate: This is the constant value applied to the gradient from the loss function that is used to adjust weights. For parameter tuning, we set this to a large number to move quickly along the cost surface in a small number of rounds. To achieve the best performance, we will set this to a lower number to make more subtle adjustments while learning new weights so we don't constantly overadjust the values.
- momentum: This uses the decaying values from previous gradients to avoid sudden shifts in movement along the cost surface. As a heuristic, a good starting value for momentum is between 0.5 and 0.8.
- eval.metric: This is the metric that you will use to evaluate performance. In our case, we are using accuracy.
Now, that we have covered the options included in our model using the mlp() function, we will make adjustments to improve accuracy. In order to improve accuracy, we will increase the number of rounds while simultaneously dropping the learning rate. We will keep the other values constant and use the node count that led to the best performance from our loop earlier. You can set the model for better performance using what we learned when parameter tuning using the following code:
model <- mx.mlp(data.matrix(train), train_target, hidden_node=90, out_node=2, out_activation="softmax",num.round=200, array.batch.size=32, learning.rate=0.005, momentum=0.8,eval.metric=mx.metric.accuracy)
preds = predict(model, data.matrix(test))
pred.label = max.col(t(preds))-1
acc = sum(pred.label == test_target)/length(test_target)
acc
After running this code, you will see a printout in your console with the accuracy score after running the model with the adjustments to the parameters. Your console output will look like this:
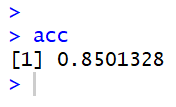
We can see that our accuracy has improved from our adjustments. Before, when we were testing parameters, the best accuracy we could achieve was 84.28%, and we can see that we now have an accuracy score of 85.01%.
After preparing our data so that it is in the proper format to model with MXNet, and then parameter tuning to find the best values for our model, we then made adjustments to further improve performance using what we learned earlier. All of these steps together describe a complete cycle of manipulating and transforming data, optimizing parameters, and then running our final model. We saw how to use MXNet, which offers a convenience function for simple MLPs and also offers the functionality to build MLPs with additional hidden layers using the activation, output, and feedforward functions.