© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_14

Speeding up Algebraic-Based Sampling via Permutations

Francesca Romana Crucinio1   and Roberto Fontana2  
(1)
Department of Statistics, University of Warwick, Coventry, CV4 7AL, UK
(2)
Dipartimento di Scienze Matematiche, Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129 Torino, Italy
 
 
Francesca Romana Crucinio (Corresponding author)
Email: F.Crucinio@Warwick.ac.uk
 
Roberto Fontana
Email: roberto.fontana@polito.it

Abstract

Algebraic sampling methods are a powerful tool to perform hypothesis tests on conditional spaces. We analyse the link of the sampling method introduced in [6] with permutation tests and we exploit this link to build a two-step sampling procedure to perform two-sample comparisons for non-negative discrete exponential families. We thus establish a link between standard permutation and algebraic-statistics-based sampling. The proposed method reduces the dimension of the space on which the MCMC sampling is performed by introducing a second step in which a standard Monte Carlo sampling is performed. The advantages of this dimension reduction are verified through a simulation study, showing that the proposed approach grants convergence in the least time and has the lowest mean squared error.

Keywords
Conditional testsDiscrete exponential familiesMarkov basisMarkov chain monte carlo

1 Introduction

Consider two samples $$\mathbf {Y}_1$$ and $$\mathbf {Y}_2$$ of size $$n_1$$ and $$n_2$$, respectively, coming from some non-negative discrete exponential family with natural parameter $$\psi (\cdot )$$, base measure $$H(\cdot )$$ and normalising constant $$G(\cdot )$$
$$\begin{aligned} f(y\mid \mu _i)=G(\mu _i)H(y)\exp \lbrace y\cdot \psi (\mu _i)\rbrace \qquad i=1,2. \end{aligned}$$
We are interested in conditional tests that exploit the joint sample $$\mathbf {Y}=(\mathbf {Y}_1, \mathbf {Y}_2)$$ of size $$N=n_1+n_2$$ to test
$$\begin{aligned} H_0: \mu =\mu _1=\mu _2\qquad \text {against} \qquad H_1: \mu _1\gtrless \mu _2. \end{aligned}$$
(1)
Specifically, there exists a uniformly most powerful unbiased (UMPU) procedure performed conditionally on the sum of the entries of the pooled sample $$T=\sum _{i=1}^{N} Y_i$$ [10]. Moreover, T is a sufficient statistic for the nuisance parameter of the test, the population constant $$\beta _0$$, if we assume the standard one-way ANOVA model for the means $$\psi (\mu _i)=\beta _0+\beta _i, \; i=1,2$$ [11].
The test statistic adopted in UMPU tests is $$U=\sum _{i=1}^{n_1} Y_i$$ and its conditional distribution given T under $$H_0$$ in (1) is
$$\begin{aligned} {f_U(u\mid T=t)=} \frac{\underset{\mathbf {y}_1\in \mathscr {F}_{n_1,u}}{\sum }\ \underset{i=1}{\overset{n_1}{\prod }}H(y_i)\cdot \underset{\mathbf {y}_2\in \mathscr {F}_{n_2,t-u}}{\sum }\ \underset{i=n_1+1}{\overset{n_1+n_2}{\prod }}H(y_i)}{\overset{t}{\underset{u=0}{\sum }}\ \underset{\mathbf {y}_1\in \mathscr {F}_{n_1,u}}{\sum }\ \underset{i=1}{\overset{n_1}{\prod }}H(y_i)\cdot \underset{\mathbf {y}_2\in \mathscr {F}_{n_2,t-u}}{\sum }\ \underset{i=n_1+1}{\overset{n_1+n_2}{\prod }}H(y_i)}, \end{aligned}$$
(2)
where H is the base measure of the non-negative discrete exponential family f. We denote by $$\mathscr {F}_{n,x}$$ the set of non-negative integer vectors of length n with sum of entries equal to x.

In order to perform the test (1), we can either find the critical values for any given risk of type I error or, alternatively, compute the p-value corresponding to the observed value $$u_{obs}$$ of U. Unfortunately, the distribution (2) can rarely be computed in closed form. In most cases, it is necessary to approximate (2) through Markov Chain Monte Carlo (MCMC).

MCMC sampling methods suffer two major drawbacks in the discrete setting: the construction of the Markov basis needed to build the chain is computationally expensive and the chain may mix slowly [8]. The idea of speeding-up the MCMC sampling is therefore not new in the Algebraic Statistics literature. In [7], the first drawback is addressed in the case of bounded contingency tables, instead of computing the entire Markov basis in an initial step, sets of local moves that connect each table in the reference set with a set of neighbouring tables are studied. A similar approach for bounded two-way contingency tables under the independence model with positive bounds is presented in [13]. A hybrid scheme using MCMC and sequential importance sampling able to address both drawbacks has been proposed in [8]. We propose a strategy that exploits the structure of the sample space for UMPU tests and does not require sequential importance sampling but only standard independent Monte Carlo sampling.

2 Markov Chain Monte Carlo Samplings

As a consequence of the conditioning on $$T=\sum _{i=1}^{n_1+n_2} Y_i$$, the sample space to be inspected under $$H_0$$, is the fibre of non-negative integer vectors of size $$N=n_1+n_2$$ and with entries which add up to t
$$\begin{aligned} \mathscr {F}_{N,t}=\lbrace (Y_1,\dots ,Y_{N})\in \mathbb {N}^{N}: \sum _{i=1}^N Y_i= \mathbf {1}_N^T \mathbf {Y}=t\rbrace , \end{aligned}$$
(3)
where $$\mathbf {1}_N=(1, \ldots , 1)$$ is the vector of length N with all entries equal to 1.
The distribution we are interested in is the cumulative distribution function of the test statistic $$U=\sum _{i=1}^{n_1} Y_i$$ given $$T=\sum _{i=1}^{N} Y_i=t$$ under $$H_0$$ as specified in (1)
$$\begin{aligned} F_U(u\mid \mathscr {F}_{N,t})=\mathbb {P}(U(\mathbf {y})\le u\mid \mathbf {y}\in \mathscr {F}_{N,t})=\sum _{\mathbf {y}\in \mathscr {F}_{N,t}}\mathbb {I}_{(U(\mathbf {y})\le u)}(\mathbf {y})f(\mathbf {y}\mid \mu ), \end{aligned}$$
(4)
where $$U(\mathbf {y})=\sum _{i=1}^{n_1}y_i$$ and $$\mathbb {I}_{(U(\mathbf {y})\le u)}(\mathbf {y})$$ is 1 if $$U(\mathbf {y})\le u$$ and 0 otherwise and $$f(\mathbf {y}\mid \mu ) = \prod _{i=1}^N f(y_i\mid \mu )$$ with a slight abuse of notation.
In the following, we describe two MCMC algorithms to sample from $$\mathscr {F}_{N,t}$$. The first one samples vectors $$\mathbf {y}\in \mathscr {F}_{N,t}$$, while the second one samples orbits of permutations $$\pi \subseteq \mathscr {F}_{N,t}$$. Both MCMC algorithms make use of a Markov basis, a set of moves allowing to build a connected Markov chain over $$\mathscr {F}_{N,t}$$ using only simple additions/subtractions [6]. Specifically, a Markov basis for a matrix A is a finite set of moves $$\lbrace \mathbf {m}_1,\ldots ,\mathbf {m}_K\rbrace $$ such that
  1. 1.

    $$\mathbf {m}_i$$ belongs to the integer kernel of A, $$1\le i\le K$$;

     
  2. 2.

    every pair of elements $$\mathbf {x}, \mathbf {y}$$ in $$\mathscr {F}_{N,t}$$ is connected by a path formed by a sequence $$(\mathbf {m}, \varepsilon )$$ of moves $$\mathbf {m}$$ and signs $$\varepsilon =\pm 1$$, and this path is contained in $$\mathscr {F}_{N,t}$$.

     

Markov bases can be found analytically [5, 6] or using the algebraic software 4ti2 [1].

2.1 MCMC—Vector-Based

The first MCMC we consider is an adaptation of the algorithm used in [2, 3, 6] for the fibre $$\mathscr {F}_{N,t}$$.
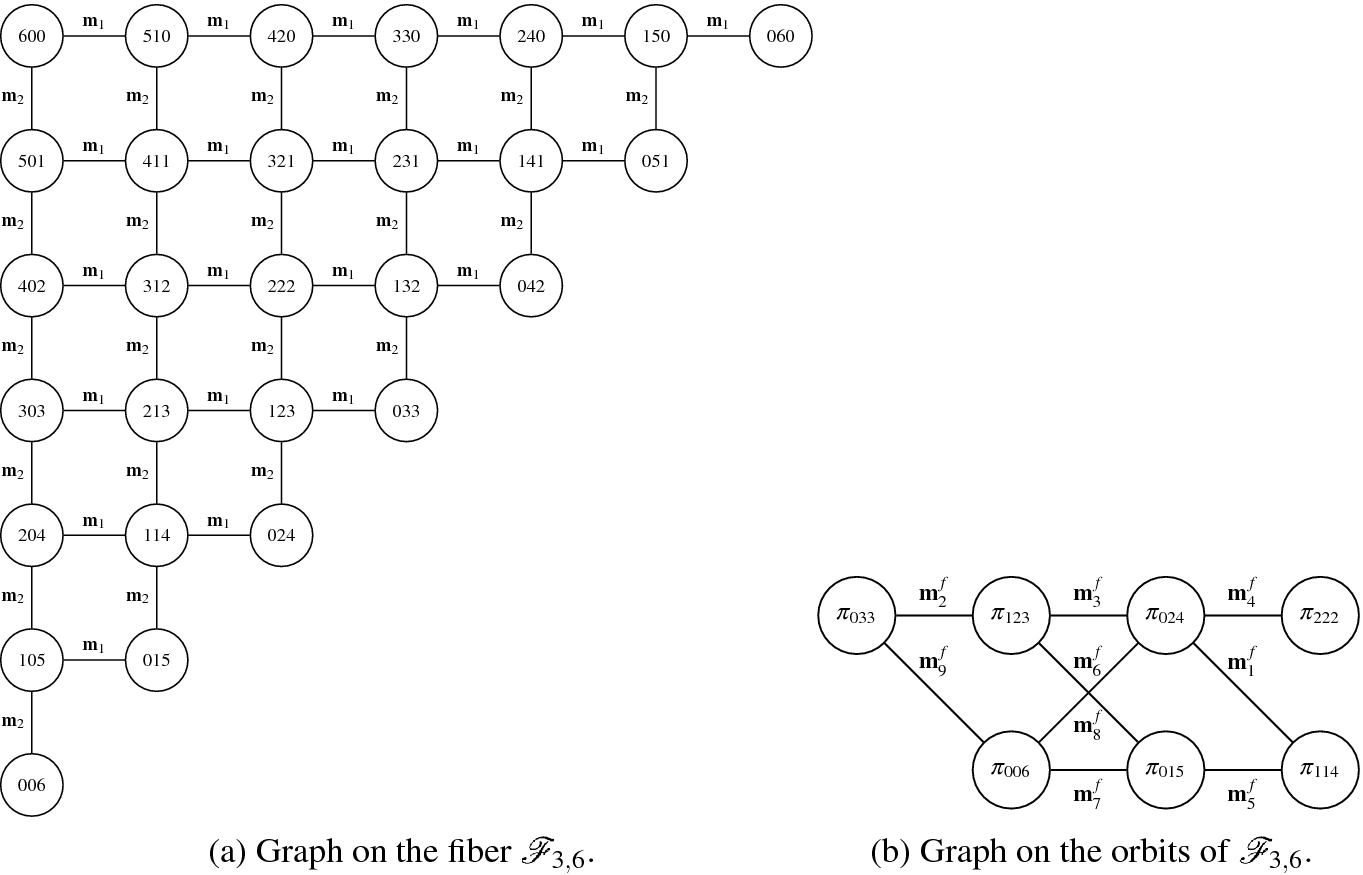
../images/461444_1_En_14_Chapter/461444_1_En_14_Fig1_HTML.png
Fig. 1

Vector-based and orbit-based parametrisation of the fibre $$\mathscr {F}_{N,t}$$

An example of the Markov chain over $$\mathscr {F}_{N,t}$$ is shown in Fig. 1a for $$N=3$$ and $$t=6$$. Each vertex of the graph represents a vector $$\mathbf {y}\in \mathscr {F}_{N,t}$$ and each edge represents an applicable move in the Markov basis. The number of states (i.e. vectors) and the number of edges is given by
$$\begin{aligned} \vert V\vert&=\left( {\begin{array}{c}t+N-1\\ N-1\end{array}}\right) \nonumber \\ \vert E\vert&=2(N-1)\left( {\begin{array}{c}t-1\\ N-1\end{array}}\right) + \sum _{z=1}^{N-1}(N-z)\left( {\begin{array}{c}t-1\\ N-1-z\end{array}}\right) \left( {\begin{array}{c}N-1\\ z-1\end{array}}\right) \left( \frac{2N-2}{z}\right) , \end{aligned}$$
respectively [5].
The target distribution of the Markov chain is the probability of sampling $$\mathbf {y}\in \mathscr {F}_{N,t}$$ under $$H_0$$ as specified in (1)
$$\begin{aligned} f(\mathbf {y}\mid \mu ) = \prod _{i=1}^N f(y_i\mid \mu )=G(\mu )^N \exp \lbrace \psi (\mu )t \rbrace \prod _{i=1}^N H(y_i)\propto \prod _{i=1}^N H(y_i). \end{aligned}$$
The estimator used to approximate (4) is the indicator function $$\mathbb {I}_{(U(\mathbf {y})\le u)}(\mathbf {y})$$, where the $$\mathbf {y}$$s are the sampled vectors.

2.2 MCMC—Orbit-Based

The second algorithm is built by exploiting the link of $$\mathscr {F}_{N,t}$$ with orbits of permutations $$\pi $$. Clearly, if $$\mathbf {y}\in \mathscr {F}_{N,t}$$, every permutation of $$\mathbf {y}$$ is an element of $$\mathscr {F}_{N,t}$$ too. Moreover, different orbits do not intersect. Therefore the orbits of permutations $$\pi \subseteq \mathscr {F}_{N,t}$$ form a partition of $$\mathscr {F}_{N,t}$$.

This partition is particularly interesting, as the elements which belong to the same orbit have the same probability of being sampled from $$\mathscr {F}_{N,t}$$, [12].

Therefore, it is possible to devise a two-step sampling procedure:  
Step 1:

Sample one orbit $$\pi $$ from the set of orbits $$\pi \subseteq \mathscr {F}_{N,t}$$.

Step 2:

Sample uniformly from $$\pi $$.

  The first step can be performed through a MCMC algorithm similar to the one described in Sect. 2.1 with target distribution the probability of sampling $$\mathbf {y}$$ in orbit $$\pi $$
$$\begin{aligned} {\sum _{\mathbf {y}\in \pi } f(\mathbf {y}\mid \mu )}, \end{aligned}$$
while the second one corresponds to a standard Monte Carlo sampling from $$\pi $$.
The number of orbits of permutation $$\pi $$ contained in the fibre is given by $$\text {part}(t,N)$$ [5], with $$\text {part}$$ defined in [9, 14]. The values of the partition function can be computed using the recurrence
$$\begin{aligned} \vert O\vert =\text {part}(t,N)=\text {part}(t,N-1)+\text {part}(t-N,N) \end{aligned}$$
and depend on both the sample size N and the sum of entries t.

To perform Step 1, we parametrise the fibre $$\mathscr {F}_{N,t}$$ in such a way that all the vectors in the same permutation orbit are mapped to the same element. To do so, we consider a frequency-based representation. In this representation the orbit $$\pi _{(0,2,4)}\subseteq \mathscr {F}_{3,6}$$ is mapped into $$\mathbf {f}_\pi =(1,0,1,0,1,0,0)$$. In this notation, vectors (0, 4, 2) and (2, 0, 4), which belong to the same orbit, correspond to the same frequency vector.

The target distribution in the frequency-based parametrisation is
$$\begin{aligned} \sum _{\mathbf {y}\in \pi } f(\mathbf {y}\mid \mu ) =\#\pi \cdot C\prod _{j=0}^t H(j)^{f_j}\propto \frac{N!}{f_0!\cdot \ldots \cdot f_t!}\prod _{j=0}^t H(j)^{f_j}, \end{aligned}$$
with $$\#\pi $$ being the number of distinct elements in the orbit $$\pi $$.
Because Step 2 corresponds to a standard permutation sampling, we consider the distribution of U given T over one orbit $$\pi $$, i.e. the usual permutation cdf,
$$\begin{aligned} F_U(u\mid \pi )=\mathbb {P}(U(\mathbf {y})\le u\mid \mathbf {y}\in \pi )=\frac{1}{\# \pi }\sum _{\mathbf {y}\in \pi }\mathbb {I}_{(U(\mathbf {y})\le u)}(\mathbf {y}). \end{aligned}$$
(5)

3 Comparison of Vector-Based and Orbit-Based MCMC

Dividing the sampling procedure into the two steps described in Sect. 2.2 has a clear computational advantage: Step 2 corresponds to a standard Monte Carlo sampling from the orbit $$\pi $$, which is faster than performing an MCMC sampling. On the other hand, Step 1 performs an MCMC sampling over the set of orbits $$\pi $$ contained in $$\mathscr {F}_{N,t}$$, whose cardinality is smaller than that of the set of vectors in $$\mathscr {F}_{N,t}$$:
$$\begin{aligned} \vert V \vert =\left( {\begin{array}{c}t+N-1\\ N-1\end{array}}\right)>\text {part}(t, N)=\vert O \vert \qquad \text {for } t,N>1. \end{aligned}$$
Table 1 shows the ratios between the cardinality of $$\pi \subseteq \mathscr {F}_{N,t}$$ and the cardinality of $$\mathbf {y}\in \mathscr {F}_{N,t}$$ for values of N and t between 5 and 100. Even for moderately sized samples, the number of orbits contained in $$\mathscr {F}_{N,t}$$ is about two orders of magnitude smaller than the number of vectors (e.g. for $$N=5$$ and $$t=5$$ $$\vert O\vert /\vert V\vert = 5.6\cdot 10^{-2}$$).
Hence, if we keep the number of iterations fixed and compare the number of vectors inspected by the two algorithms, the orbit-based algorithm gives the highest value, namely the number of iterations $$\times $$ the number of distinct vectors in the orbit sampled at iteration i.
Table 1

Ratio between the number of orbits $$\vert O\vert $$ and the number of vectors $$\vert V\vert $$ in $$\mathscr {F}_{N,t}$$ for several values of N and t

$$\mathbf {N\ \backslash \ t}$$

5

10

15

20

30

50

100

5

0.056

0.030

0.022

0.018

0.015

0.012

0.010

10

0.004

$$4.5\cdot 10^{-4}$$

$$1.3\cdot 10^{-4}$$

$$5.3\cdot 10^{-5}$$

$$1.7\cdot 10^{-5}$$

$$5.0\cdot 10^{-6}$$

$$1.5\cdot 10^{-6}$$

15

$$6.0\cdot 10^{-4}$$

$$2.1\cdot 10^{-5}$$

$$2.3\cdot 10^{-6}$$

$$4.4\cdot 10^{-7}$$

$$4.4\cdot 10^{-8}$$

$$2.9\cdot 10^{-9}$$

$$1.4\cdot 10^{-10}$$

20

$$1.6\cdot 10^{-4}$$

$$2.1\cdot 10^{-6}$$

$$9.5\cdot 10^{-8}$$

$$9.1\cdot 10^{-9}$$

$$2.9\cdot 10^{-10}$$

$$3.9\cdot 10^{-12}$$

$$2.0\cdot 10^{-14}$$

50

$$2.2\cdot 10^{-6}$$

$$6.7\cdot 10^{-10}$$

$$1.1\cdot 10^{-12}$$

$$5.4\cdot 10^{-15}$$

$$1.0\cdot 10^{-18}$$

$$4.0\cdot 10^{-24}$$

$$2.8\cdot 10^{-32}$$

We show how the reduction in the dimension of the space explored by the MCMC algorithm improves convergence and accuracy with respect to the truth (4) through the simulation study in the next section.

4 Simulation Study

Assume that the two samples $$\mathbf {Y}_1$$ and $$\mathbf {Y}_2$$ are Poisson distributed with mean $$\mu _1$$ and $$\mu _2$$, respectively. In this case, the exact distribution (4) under $$H_0$$ is the binomial distribution
$$\begin{aligned} F_U(u\mid \mathscr {F}_{N,t})=\mathbb {P}(\text {Binomial}(t,\theta _0)\le u)=\sum _{k=0}^u \left( {\begin{array}{c}t\\ k\end{array}}\right) \theta _0^k(1-\theta _0)^{t-k}, \end{aligned}$$
(6)
with $$\theta _0=n_1/(n_1+n_2)$$ [10, 11].

We compare the exact conditional cdf above with the approximated cdfs given by the vector-based algorithm, the orbit-based algorithm and the standard permutation cdf over the orbit of the observed pooled vector (this is the limit case of the orbit-based algorithm when only the observed orbit is sampled). A preliminary simulation study is presented in [4].

We consider 9 scenarios built taking three sample sizes $$(n_1,n_2)$$ and, for each sample size, three different couples of population means $$(\mu _1,\mu _2)$$.

The comparisons performed are two: first, we check the convergence behaviour on a fixed runtime (15 s) for both algorithms; then we compare their accuracy through the mean squared error (MSE).

4.1 Convergence Comparison

To compare how fast the two MCMC procedures converge to the true distribution (4), we draw one random sample $$\mathbf {y}_{obs}$$ for each scenario above and we run both algorithms for 15 s. Figure 2 shows four examples of the behaviour of the two MCMC procedures which are representative of the nine scenarios.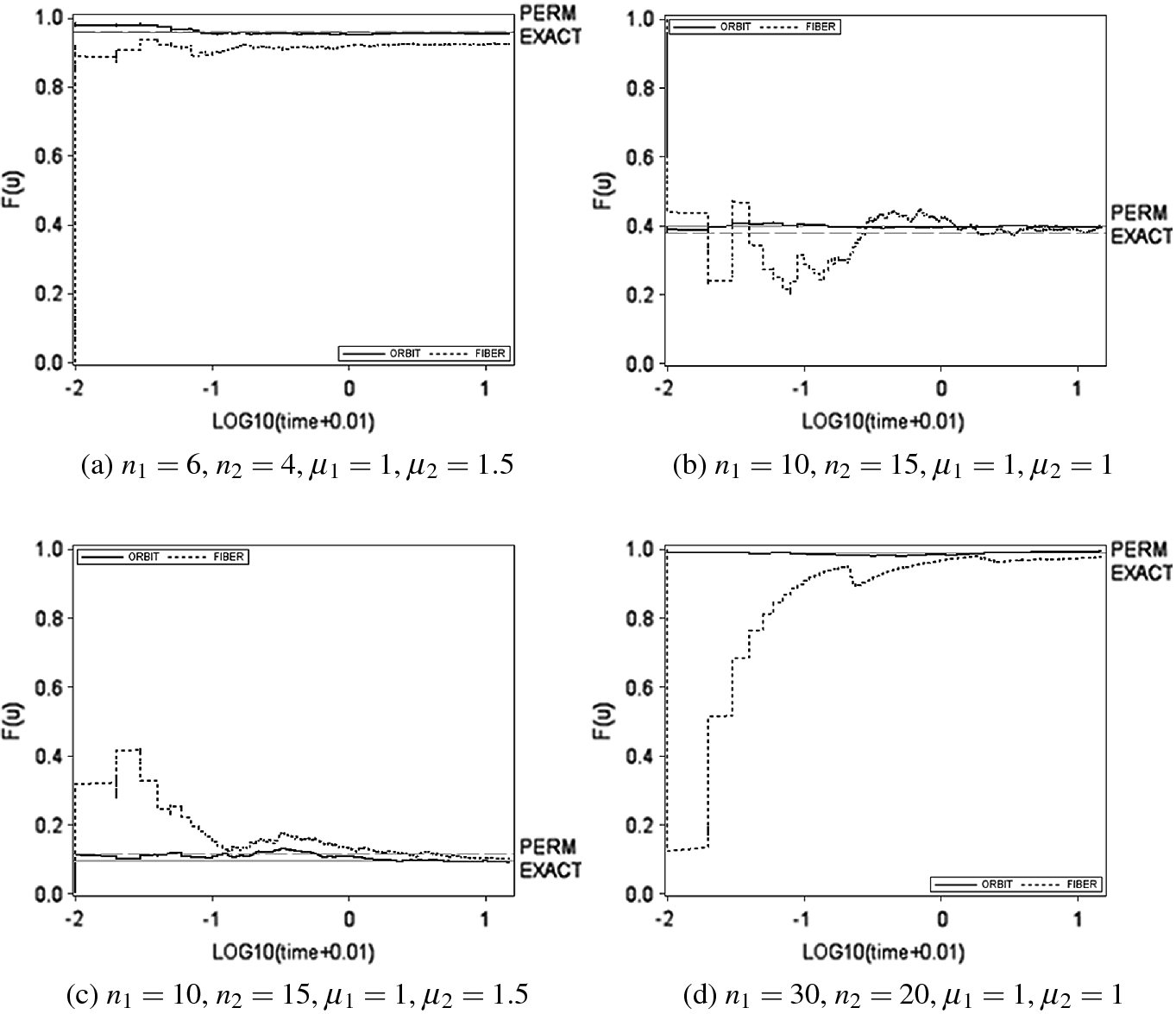
../images/461444_1_En_14_Chapter/461444_1_En_14_Fig2_HTML.png
Fig. 2

Comparison of the convergence to the exact value (solid horizontal line) in 15 s for the vector-based algorithm (dashed line) and the orbit-based algorithm (solid line). The Monte Carlo permutation estimate of $$F_U(u\mid \mathscr {F}_{N,t})$$ (dashed horizontal line) is reported too. The number of Monte Carlo permutations per orbit is 5, 000. The plots show the estimates achieved as functions of the log-time

The orbit-based algorithm is very fast and achieves good convergence in $$\sim 0.1$$ seconds. On the contrary, the vector-based algorithm is much less efficient, in fact, its convergence to the exact value is not always satisfactory even after 15 s (Fig. 2a, b).

Remark 1

It would be possible to further reduce the computational time required by the orbit-based algorithm by exploiting one of the key features of this new approach, namely the possibility of sampling from each orbit independently. The Monte Carlo samplings in Step 2 could be made in parallel: once the chain reaches an orbit $$\pi $$ the Monte Carlo sampling over $$\pi $$ can be performed while the chain keeps on moving on the set of orbits.

4.2 Accuracy Comparison

For each scenario, we randomly generate 1, 000 samples through which we compute the MSE of the distribution estimated by the three procedures under study
$$\begin{aligned} \text {MSE} = \frac{1}{1000}\sum _{j=1}^{1000}\left( \sum _{k=0}^{u_j} \left( {\begin{array}{c}t_j\\ k\end{array}}\right) \theta _0^k(1-\theta _0)^{t_j-k}\ -\ \hat{F}_U(u_j\mid \mathscr {F}_{N, t_j})\right) ^2. \end{aligned}$$
Both MCMC algorithms are run for 15 s with no burn-in steps. The resulting MSE for the nine scenarios is shown in Table 2. As a further comparison, we report the MSE given by the standard Monte Carlo permutation sampling over the observed orbit.
Table 2

Mean Squared Error (MSE) for the vector-based, the orbit-based and the Monte Carlo permutation sampling. Both MCMC algorithms were run for 15 s with no burn-in steps

$$n_1$$

$$n_2$$

$$\mu _1$$

$$\mu _2$$

Orbit-based

Vector-based

Permutation

6

4

1

1

0.00012

0.0016

0.00284

6

4

1

1.5

0.00012

0.00083

0.00212

6

4

1

2

0.00016

0.00043

0.00221

10

15

1

1

0.00034

0.00131

0.00077

10

15

1

1.5

0.00009

0.00046

0.00074

10

15

1

2

0.00007

0.00017

0.00057

20

30

1

1

0.00069

0.00132

0.00036

20

30

1

1.5

0.00006

0.00053

0.00027

20

30

1

2

0.00001

0.00011

0.00009

The orbit-based algorithm always give the smallest MSE apart from scenario $$n_1=20$$, $$n_2=30$$, $$\mu _1=1$$, $$\mu _2=1$$, where the standard Monte Carlo permutation sampling has the smallest MSE. Table 3 shows the ratio between the MSE of the vector-based algorithm and the MSE of the orbit-based algorithm (column 5) and the ratio between the MSE of the standard Monte Carlo permutation sampling and the MSE of the orbit-based algorithm (column 6). The MSE of the vector-based algorithm is at least 1.9 times bigger than that of the orbit-based algorithm, while the MSE of the standard Monte Carlo permutation sampling can be 22.7 times bigger than that of the orbit-based algorithm (scenario 1).
Table 3

Ratio between the MSE of the vector-based and the MSE of the orbit-based algorithm (column 5) and ratio between the MSE of the standard Monte Carlo permutation sampling and the MSE of the orbit-based algorithm (column 6).

$$n_1$$

$$n_2$$

$$\mu _1$$

$$\mu _2$$

MSE vector/MSE orbit

MSE perm/MSE orbit

6

4

1

1

12.82

22.7

6

4

1

1.5

6.98

17.79

6

4

1

2

2.67

13.82

10

15

1

1

3.9

2.31

10

15

1

1.5

4.96

8

10

15

1

2

2.45

8.27

20

30

1

1

1.9

0.52

20

30

1

1.5

9.03

4.58

20

30

1

2

15.9

12.77

The number of iterations made by the vector-based and the orbit-based algorithms in the allocated 15 s are reported in Table 4. The orbit-based algorithm performs better than the vector-based one even if the number of iterations made is lower: in 15 s, the ratio between the numbers of iterations increases from twice to almost 19 times. Despite this difference in the number of iterations, the orbit-based algorithm always achieves lower MSE than the vector-based algorithm.
Table 4

Number of iterations for 15 s

Scenario

N. iterations

Ratio

$$n_1$$

$$n_2$$

$$\mu _1$$

$$\mu _2$$

Orbit

Vector

Vector/Orbit

6

4

1

1

23,977

53,842

2.25

6

4

1

1.5

24,169

53,210

2.20

6

4

1

2

24,560

57,382

2.34

10

15

1

1

11,950

52,504

4.39

10

15

1

1.5

11,564

54,836

4.74

10

15

1

2

7326

53,492

7.30

20

30

1

1

4675

45,576

9.75

20

30

1

1.5

3174

44,817

14.12

20

30

1

2

2572

48,003

18.66

5 Conclusions

The orbit-based algorithm grants a faster convergence to the exact distribution if compared to the standard MCMC algorithm proposed in [6]. At the same time, it gives more reliable estimates by decreasing the MSE. This simulation-based observation can be proved by comparing the variance of the estimators used by the two algorithms (the indicator function in (4) and the permutation cdf (5) respectively) [5].

When permutation-invariant statistics are used, the orbit-based algorithm is dramatically simplified. In this case, it is only necessary to walk among orbits of permutations without performing the second-step sampling and thus the reduction in computational time is significant.

Finally, it is worth noting that the MCMC sampling procedure based on orbits of permutations establishes a link between standard permutation and algebraic-statistics-based sampling that, to the best of our knowledge, has not been previously noted.

A preliminary version of this work has been presented at the 4th ISNPS conference in June 2018 in Salerno, Italy. Extensions of the present work include hypothesis testing for $$K>2$$ groups and data fitting [5].

Acknowledgments

R. Fontana acknowledges that the present research has been partially supported by MIUR grant Dipartimenti di Eccellenza 2018–2022 (E11G18000350001). The authors thank the anonymous referee for his/her helpful comments.