1 Introduction
Due to its natural intermittency, the estimation of a non-uniform density can be described as a nonequispaced multiscale problem, especially when the density contains singularities. Indeed, when the number and the locations of the singularities remain unknown, then the estimation procedure is deemed to go through all possible combinations of locations and intersingular distances. Also, since a given bandwidth in a kernel-based method may be too small in a region of low intensity and too large in a region of high intensity, a local choice of the bandwidth can be considered as an instance of multiscale processing, where the bandwidth is seen as a notion of scale.
A popular class of multiscale methods in smoothing and density estimation is based on a wavelet analysis of the data. The classical wavelet approach for density estimation [3, 6] requires an evaluation of the wavelet basis functions in the observed data or otherwise a binning of the data into fine scale intervals, defined by equispaced knots on which the wavelet transform can be constructed. The preprocessing for the equispaced (and possibly dyadic) wavelet analysis may induce some loss of details about the exact values of the observations.
This paper works with a family of multiscale transforms constructed on nonequispaced knots. With these constructions and taking the observations as knots, no information is lost at this stage of the analysis. The construction of wavelet transforms on irregular point sets is based on the lifting scheme [11, 12]. Given the transformation matrix that maps a wavelet approximation at one scale onto the approximation and offsets at the next coarser scale, the lifting scheme factorizes this matrix into a product of simpler, readily invertible operations. Based on the lifting factorization, there exist two main directions in the design of wavelets on irregular point sets. The first direction consists of the factorization of basis functions that are known to be refinable, to serve as approximation basis, termed scaling basis in a wavelet analysis. The wavelet basis for the offsets between successive scales is then constructed within the lifting factorization of the refinement equation, taking into account typical design objectives such as vanishing moments and control of variance inflation. Examples of such existing refinable functions are B-spline functions defined on nested grids of knots [8]. The second approach for the construction of wavelets on irregular point sets does not factorize a scheme into lifting steps. Instead, it uses an interpolating or smoothing scheme as a basic tool in the construction of a lifting step from scratch. Using interpolating polynomials leads to the Deslauriers-Dubuc refinement scheme [2, 4]. To this refinement scheme, a wavelet transform can be associated by adding a single lifting step, designed for vanishing moments and control of variance inflation, as in the case of factorized refinement schemes. This paper follows the second approach, using local polynomial smoothing [5, Chapter 3] as a basic tool in a lifting scheme. For reasons explained in Sect. 2, the resulting Multiscale Local Polynomial Transform (MLPT) is no longer a wavelet transform in the strict sense, as it must be slightly overcomplete. Then, in Sect. 3, the density estimation problem is reformulated in a way that it can easily be handled by an MLPT. Section 4 discusses aspects of sparse selection and estimation in the MLPT domain for data from a density estimation problem. In Sect. 5, the sparse selection is finetuned, using information criteria and defining the degrees of freedom in this context. Finally, Sect. 6 presents some preliminary simulation results and further outlook.
2 The Multiscale Local Polynomial Transform (MLPT)
 be a sample vector from the additive model
be a sample vector from the additive model  , where the covariates
, where the covariates  may be non-equidistant and the noise
may be non-equidistant and the noise  may be correlated. The underlying function, f(x), is assumed to be approximated at resolution level J by a linear combination of basis functions
may be correlated. The underlying function, f(x), is assumed to be approximated at resolution level J by a linear combination of basis functions  , in
, in
 is a row vector containing the basis functions. The choice of coefficients
is a row vector containing the basis functions. The choice of coefficients  is postponed to the moment when the basis functions are specified. At this moment, one could think of a least squares projection as one of the possibilities.
is postponed to the moment when the basis functions are specified. At this moment, one could think of a least squares projection as one of the possibilities. in
in  , using a linear operation
, using a linear operation  . Just like in wavelet decomposition, the coefficient vector of several subvectors
. Just like in wavelet decomposition, the coefficient vector of several subvectors ![$$\textit{\textbf{v}} = [\begin{array}{ccccc} \textit{\textbf{s}}_L^T&\textit{\textbf{d}}_L^T&\textit{\textbf{d}}_{L+1}^T&\ldots&\textit{\textbf{d}}_{J-1}^T\end{array}]^T$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq11.png) , leading to the following basis transformation
, leading to the following basis transformation
 and
and  for the submatrices of the transformed basis
for the submatrices of the transformed basis  , corresponding to the subvectors of the coefficient vector
, corresponding to the subvectors of the coefficient vector  . The detail vectors
. The detail vectors  are associated to successive resolution levels through the decomposition algorithm, corresponding to the analysis matrix
are associated to successive resolution levels through the decomposition algorithm, corresponding to the analysis matrix  ,
,
Subsamplings, i.e., keep a subset of the current approximation vector,
 , with
, with  a
a  submatrix of the identity matrix.
submatrix of the identity matrix.Prediction, i.e., compute the detail coefficients at scale j as offsets from a prediction based on the subsample.

Update, the remaining approximation coefficients. The idea is that
 can be interpreted as smoothed, filtered, or averaged values of
can be interpreted as smoothed, filtered, or averaged values of  .
. 
Before elaborating on the different steps of this decomposition, we develop the inverse transform  by straightforwardly undoing the two lifting steps in reverse order.
by straightforwardly undoing the two lifting steps in reverse order.

Undo update, using
 .
.Undo prediction, using
 .
.
2.1 Local Polynomial Smoothing as Prediction

 is the bandwidth. While in (uniscale) kernel smoothing this is a smoothing parameter, aiming at optimal balance between bias and variance in the estimation, it acts as a user-controlled scale parameter in a Multiscale Kernel Transform (MKT). This is in contrast to a discrete wavelet transform, where the scale is inherently fixed to be dyadic, i.e., the scale at level j is twice the scale at level
is the bandwidth. While in (uniscale) kernel smoothing this is a smoothing parameter, aiming at optimal balance between bias and variance in the estimation, it acts as a user-controlled scale parameter in a Multiscale Kernel Transform (MKT). This is in contrast to a discrete wavelet transform, where the scale is inherently fixed to be dyadic, i.e., the scale at level j is twice the scale at level  . In an MKT, and also in the forthcoming MLPT, the scale can be chosen in a data adaptive way, taking the irregularity of the covariate grid into account. For instance, when the covariates can be considered as ordered independent realizations from a uniform density, it is recommended that the scale is taken to be
. In an MKT, and also in the forthcoming MLPT, the scale can be chosen in a data adaptive way, taking the irregularity of the covariate grid into account. For instance, when the covariates can be considered as ordered independent realizations from a uniform density, it is recommended that the scale is taken to be  [10]. The scales at fine resolution levels are then a bit larger, allowing them cope up with the non-equidistance of the covariates.
[10]. The scales at fine resolution levels are then a bit larger, allowing them cope up with the non-equidistance of the covariates. with
with  , where the row vector
, where the row vector  is given by
is given by
![$$\textit{\textbf{X}}^{(\tilde{p})}(x) = [1~~x~~\ldots ~~x^{\tilde{p}-1}]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq36.png) and the corresponding Vandermonde matrix at resolution level j,
and the corresponding Vandermonde matrix at resolution level j, ![$$ \mathbf {X}_j^{(\tilde{p})} = [\textit{\textbf{1}}~~\textit{\textbf{x}}_j~~\ldots ~~\textit{\textbf{x}}_j^{\tilde{p}-1}]. $$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq37.png) The diagonal matrix of weight functions is given by
The diagonal matrix of weight functions is given by 
The prediction matrix has dimension  . This expansive or redundant prediction is in contrast to lifting schemes for critically downsampled wavelet transform, such as the Deslauriers–Dubuc or B-spline refinement schemes. In these schemes, the prediction step takes the form
. This expansive or redundant prediction is in contrast to lifting schemes for critically downsampled wavelet transform, such as the Deslauriers–Dubuc or B-spline refinement schemes. In these schemes, the prediction step takes the form  , where
, where  , with
, with  the
the  subsampling operation, complementary to
subsampling operation, complementary to  . In the MLPT, a critical downsampling with
. In the MLPT, a critical downsampling with  and
and  would lead to fractal-like basis functions
[7]. The omission of the complementary subsampling leads to slight redundancy, where n data points are transformed into roughly 2n MLPT coefficients, at least if
would lead to fractal-like basis functions
[7]. The omission of the complementary subsampling leads to slight redundancy, where n data points are transformed into roughly 2n MLPT coefficients, at least if  is approximately half of
is approximately half of  at each scale. The corresponding scheme is known in signal processing literature as the Laplacian pyramid
[1]. With an output size of 2n, the MLPT is less redundant than the non-decimated wavelet transform (cycle spinning, stationary wavelet transform) which produces outputs of size
at each scale. The corresponding scheme is known in signal processing literature as the Laplacian pyramid
[1]. With an output size of 2n, the MLPT is less redundant than the non-decimated wavelet transform (cycle spinning, stationary wavelet transform) which produces outputs of size  . Nevertheless, the inverse MLPT shares with the non-decimated wavelet transform an additional smoothing occurring in the reconstruction after processing. This is because processed coefficients are unlikely to be exact decompositions of an existing data vector. The reconstruction thus involves some sort of projection.
. Nevertheless, the inverse MLPT shares with the non-decimated wavelet transform an additional smoothing occurring in the reconstruction after processing. This is because processed coefficients are unlikely to be exact decompositions of an existing data vector. The reconstruction thus involves some sort of projection.
2.2 The Update Lifting Step
The second lifting step, the update  , serves multiple goals, leading to a combination of design conditions
[8]. An important objective, especially in the context of density estimation, is to make sure that all functions in
, serves multiple goals, leading to a combination of design conditions
[8]. An important objective, especially in the context of density estimation, is to make sure that all functions in  have zero integral. When
have zero integral. When  , then any processing that modifies the detail coefficients
, then any processing that modifies the detail coefficients  , e.g., using thresholding, preserves the integral of
, e.g., using thresholding, preserves the integral of  , which is interesting if we want to impose that
, which is interesting if we want to impose that  for an estimation or approximation of a density function. Another important goal of the update, leading to additional design conditions, is to control the variance propagation throughout the transformation. This prevents the noise from a single observation from proceeding unchanged all the way to coarse scales.
for an estimation or approximation of a density function. Another important goal of the update, leading to additional design conditions, is to control the variance propagation throughout the transformation. This prevents the noise from a single observation from proceeding unchanged all the way to coarse scales.
2.3 The MLPT Frame
 and
and  . Also, as the detail functions form an overcomplete set, they are not basis functions in the strict sense. Instead, the set of
. Also, as the detail functions form an overcomplete set, they are not basis functions in the strict sense. Instead, the set of  and
and  for
for  is called a frame.
is called a frame.
Left panel: approximation function, i.e., one element of  . Right panel: detail or offset function, i.e., one element of
. Right panel: detail or offset function, i.e., one element of  . It holds that
. It holds that 

2.4 The MLPT on Highly Irregular Grids
The regression formulation of the density estimation problem in Sect. 3 will lead to regression on highly irregular grids, that is, grids that are far more irregular than ordered observations from a random variable. On these grids, it is not possible to operate at fine scales, even if these scales are a bit wider than in the equidistant case, as discussed in Sect. 2.1. In order to cope with the irregularity, the fine scales would be so wide that fine details are lost, and no asymptotic result would be possible. An alternative solution, adopted here, is to work with dyadic scales, but only processing coefficients that have sufficient nearby neighbors within the current scale. Coefficients in sparsely sampled neighborhoods are forwarded to coarser scales. The implementation of such a scheme requires the introduction of a smooth transition between active and non-active areas at each scale [9].
 , is replaced by a weighted form
, is replaced by a weighted form
 has values between 0 and 1. The value is 0 when a coefficient is not surrounded by enough neighbors to apply a regular local polynomial prediction
has values between 0 and 1. The value is 0 when a coefficient is not surrounded by enough neighbors to apply a regular local polynomial prediction  , and it gradually (not suddenly, that is) tends to one in areas with sufficiently dense observations to apply proper polynomial prediction.
, and it gradually (not suddenly, that is) tends to one in areas with sufficiently dense observations to apply proper polynomial prediction.3 A Regression Model for Density Estimation
Let  be a sample of independent realization from an unknown density
be a sample of independent realization from an unknown density  on a bounded interval, which we take, without loss of generality, to be [0, 1]. The density function has an unknown number of singularities, i.e., points
on a bounded interval, which we take, without loss of generality, to be [0, 1]. The density function has an unknown number of singularities, i.e., points ![$$x_0 \in [0,1]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq69.png) where
where  , as well as other discontinuities.
, as well as other discontinuities.
As in
[9], we consider the spacings  , i.e., the differences between the successive ordered observations
, i.e., the differences between the successive ordered observations  . Then, by the mean value theorem, we have that there exists a value
. Then, by the mean value theorem, we have that there exists a value ![$$\overline{\xi }_{n;i} \in [X_{(n;i-1)},X_{(n;i)}]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq73.png) for which
for which  , where
, where  . Unfortunately, the value of
. Unfortunately, the value of  cannot be used as such in the subsequent asymptotic result, due to technical issues in the proof. Nevertheless, for a fairly free choice of
cannot be used as such in the subsequent asymptotic result, due to technical issues in the proof. Nevertheless, for a fairly free choice of ![$$\xi _{n;i} \in [X_{(n;i-1)},X_{(n;i)}]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq77.png) , close to
, close to  , the theorem provides nonparametric regression of
, the theorem provides nonparametric regression of  on
on  . For details on the proof, we refer to
[9].
. For details on the proof, we refer to
[9].
Let  be an almost everywhere twice continuously differentiable density function on
be an almost everywhere twice continuously differentiable density function on ![$$x \in [0,1]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq82.png) . Define
. Define ![$$A_{M,\delta } \subset [0,1]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq83.png) as the set where
as the set where  and
and  , with
, with  arbitrary, strictly positive real numbers. Then there exist values
arbitrary, strictly positive real numbers. Then there exist values ![$$\xi _{n;i} \in [X_{(n;i-1)},X_{(n;i)}]$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq87.png) , so that with probability one, for all intervals
, so that with probability one, for all intervals ![$$[X_{(n;i-1)},X_{(n;i)}] \subset A_{M,\delta }$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq88.png) ,
,
 , given the covariate
, given the covariate  , converges in distribution to an exponential random variable, i.e.,
, converges in distribution to an exponential random variable, i.e.,
We thus consider a model with exponentially distributed response variable  and the vector of parameters
and the vector of parameters  with
with  , for which we propose a sparse MLPT model
, for which we propose a sparse MLPT model  , with
, with  the inverse MLPT matrix defined on the knots in
the inverse MLPT matrix defined on the knots in  .
.
The formulation of the density estimation problem as a sparse regression model induces no binning or any other loss of information. On the contrary, the information on the values of  is duplicated: a first, approximative copy can be found in the covariate values
is duplicated: a first, approximative copy can be found in the covariate values  . A second copy defines the design matrix. The duplication prevents loss of information when in subsequent steps some sort of binning is performed on the response variables.
. A second copy defines the design matrix. The duplication prevents loss of information when in subsequent steps some sort of binning is performed on the response variables.
4 Sparse Variable Selection and Estimation in the Exponential Regression model
 with
with  , and
, and  , the score is given by
, the score is given by  , so that the maximum
, so that the maximum  regularized log-likelihood estimator
regularized log-likelihood estimator  can be found by solving the Karush–Kuhn–Tucker (KKT) conditions
can be found by solving the Karush–Kuhn–Tucker (KKT) conditions
 were nonzero, the KKT would still be highly nonlinear. This is in contrast to the additive normal model, where
were nonzero, the KKT would still be highly nonlinear. This is in contrast to the additive normal model, where  . The estimator given the selection then follows from a shrunk least squares solution. Indeed, with
. The estimator given the selection then follows from a shrunk least squares solution. Indeed, with  the set of selected components, we have
the set of selected components, we have  where
where  is the soft-threshold function. In the case of orthogonal design, i.e., when
is the soft-threshold function. In the case of orthogonal design, i.e., when  is the identity matrix, and this reduces to straightforward soft-thresholding in the transformed domain. In the case of non-orthogonal, but still Riesz-stable, design, straightforward thresholding is still a good approximation and a common practice, for instance, in B-spline wavelet thresholding. For the model with exponential response, the objective is to find appropriate values of
is the identity matrix, and this reduces to straightforward soft-thresholding in the transformed domain. In the case of non-orthogonal, but still Riesz-stable, design, straightforward thresholding is still a good approximation and a common practice, for instance, in B-spline wavelet thresholding. For the model with exponential response, the objective is to find appropriate values of  , so that
, so that  can be used as an estimator. For this we need at least that
can be used as an estimator. For this we need at least that - (C1)
the expected value of
 is close to
is close to  , so that
, so that 
- (C2)
the MLPT decomposition
 is sparse,
is sparse,- (C3)
the MLPT decomposition of the errors,
 has no outliers, i.e., no heavy tailed distributions.
has no outliers, i.e., no heavy tailed distributions.
 , it may be interesting to start the search for appropriate fine scale coefficients
, it may be interesting to start the search for appropriate fine scale coefficients  from
from ![$$S_{J,i}^{[0]} = 1/Y_i$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq120.png) . Unfortunately,
. Unfortunately, ![$$S_{J,i}^{[0]}$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq121.png) is heavy tailed. Experiments show that the heavy tails cannot be dealt properly by truncation of
is heavy tailed. Experiments show that the heavy tails cannot be dealt properly by truncation of  in
in ![$$S_{J,i}^{[1]} = \min (1/Y_i,s_{\max })$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_IEq123.png) without loss of substantial information about the position and nature of the singular points in the density function.
without loss of substantial information about the position and nature of the singular points in the density function. through the covariate values in the design
through the covariate values in the design  . More precisely, let
. More precisely, let![$$\begin{aligned} \textit{\textbf{S}}_J = \varvec{\Pi }\mathbf {D}_{h_{J,0}}\widetilde{\varvec{\Pi }} \textit{\textbf{S}}_J^{[0]}. \end{aligned}$$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_Equ2.png)
 and
and  represent a forward and inverse, one coefficient at-a-time, unbalanced Haar transform defined on the data adaptive knots
represent a forward and inverse, one coefficient at-a-time, unbalanced Haar transform defined on the data adaptive knots  and
and  . An Unbalanced Haar transform on the vector of knots
. An Unbalanced Haar transform on the vector of knots  is defined by
is defined by
 and
and  . In the coefficient at-a-time version, the binning operation
. In the coefficient at-a-time version, the binning operation  takes place on a single pair
takes place on a single pair  and
and  , chosen so that
, chosen so that  is as small as possible. Finally, the diagonal matrix
is as small as possible. Finally, the diagonal matrix  in (2), replaces all details
in (2), replaces all details  by zero for which the scale
by zero for which the scale  is smaller than a minimum width
is smaller than a minimum width  . The overall effect of (2) is that small values in
. The overall effect of (2) is that small values in  are recursively added to their neighbors until all binned values are larger than
are recursively added to their neighbors until all binned values are larger than  . For values of
. For values of  sufficiently large, it can be analyzed that the coefficients of
sufficiently large, it can be analyzed that the coefficients of  are close to being normally distributed with expected value asymptotically equal to
are close to being normally distributed with expected value asymptotically equal to  and variance asymptotically equal to
and variance asymptotically equal to  [9]. Unfortunately, a large value of
[9]. Unfortunately, a large value of  also introduces binning bias. In order to reduce this bias and to let
also introduces binning bias. In order to reduce this bias and to let  be sufficiently large, the choice of
be sufficiently large, the choice of  is combined with a limit on the number of observations in one bin
[9].
is combined with a limit on the number of observations in one bin
[9].5 Fine-Tuning the Selection Threshold
The estimator  applies a threshold on the MLPT of
applies a threshold on the MLPT of  . The input
. The input  is correlated and heteroscedastic, while the transform is not orthogonal. For all these reasons, the errors on
is correlated and heteroscedastic, while the transform is not orthogonal. For all these reasons, the errors on  are correlated and heteroscedastic. In an additive normal model where variance and mean are two separate parameters, the threshold would be taken proportional to the standard deviation. In the context of the exponential model with approximate variance function
are correlated and heteroscedastic. In an additive normal model where variance and mean are two separate parameters, the threshold would be taken proportional to the standard deviation. In the context of the exponential model with approximate variance function  , coefficients with large variances tend to carry more information, i.e., they have a larger expected value as well. As a result, there is no argument for a threshold linearly depending on the local standard deviation. This paper adopts a single threshold for all coefficients to begin with. Current research also investigates the use of block thresholding methods.
, coefficients with large variances tend to carry more information, i.e., they have a larger expected value as well. As a result, there is no argument for a threshold linearly depending on the local standard deviation. This paper adopts a single threshold for all coefficients to begin with. Current research also investigates the use of block thresholding methods.
The threshold or any other selection parameter can be finetuned by optimization of the estimated distance between the data generating process and the model under consideration. The estimation of that distance leads to an information criterion. This paper works with an Akaike’s Information Criterion for the estimation of the Kullback–Leibler distance. As data generating process, we consider the (asymptotic) independent exponential model for the spacings, and not the asymptotic additive, heteroscedastic normal model for  . This choice is motivated by the fact that a model for
. This choice is motivated by the fact that a model for  is complicated as it should account for the correlation structure, while the spacings are nearly independent. Moreover, fine-tuning w.r.t. the spacings is not affected by the loss of information in the computation of
is complicated as it should account for the correlation structure, while the spacings are nearly independent. Moreover, fine-tuning w.r.t. the spacings is not affected by the loss of information in the computation of  .
.
 The first term is the empirical log-likelihood
The first term is the empirical log-likelihood![$$ \widehat{\ell }(\widehat{\varvec{\theta }}) = \sum _{i=1}^n \left[ \log (\widehat{\theta }_i) - \widehat{\theta }_iY_i\right] , $$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_Equ11.png)
![$$ \nu (\widehat{\varvec{\theta }}) = E\left[ \widehat{\varvec{\theta }}^T(\varvec{\mu }-\textit{\textbf{Y}})\right] . $$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_Equ12.png)
 as estimator of the expected log-likelihood has taken over the unknown data generating process. The expected log-likelihood in its turn is the part of the Kullback–Leibler distance that depends on the estimated parameter vector.
as estimator of the expected log-likelihood has taken over the unknown data generating process. The expected log-likelihood in its turn is the part of the Kullback–Leibler distance that depends on the estimated parameter vector.An estimator of the degrees of freedom is developed in [9],
![$$ \widehat{\nu }(\widehat{\varvec{\theta }}) = \mathrm {Tr}\left[ \mathbf {D}_{\lambda }\widetilde{\mathbf {X}} \overline{\mathbf {\Upsilon }}^{-2}\widetilde{\mathbf {Q}}\mathbf {\Upsilon } \widehat{\mathbf {\Theta }}^{-1}\mathbf {X}\right] , $$](../images/461444_1_En_23_Chapter/461444_1_En_23_Chapter_TeX_Equ13.png)
 is a diagonal matrix with slightly shifted versions of the observed values, i.e.,
is a diagonal matrix with slightly shifted versions of the observed values, i.e.,  . The matrix
. The matrix  is a diagonal matrix with the observations, i.e.,
is a diagonal matrix with the observations, i.e.,  . The diagonal matrix
. The diagonal matrix  has zeros and ones on the diagonal. The ones correspond to nonzero coefficients in the thresholded MLPT decomposition.
has zeros and ones on the diagonal. The ones correspond to nonzero coefficients in the thresholded MLPT decomposition.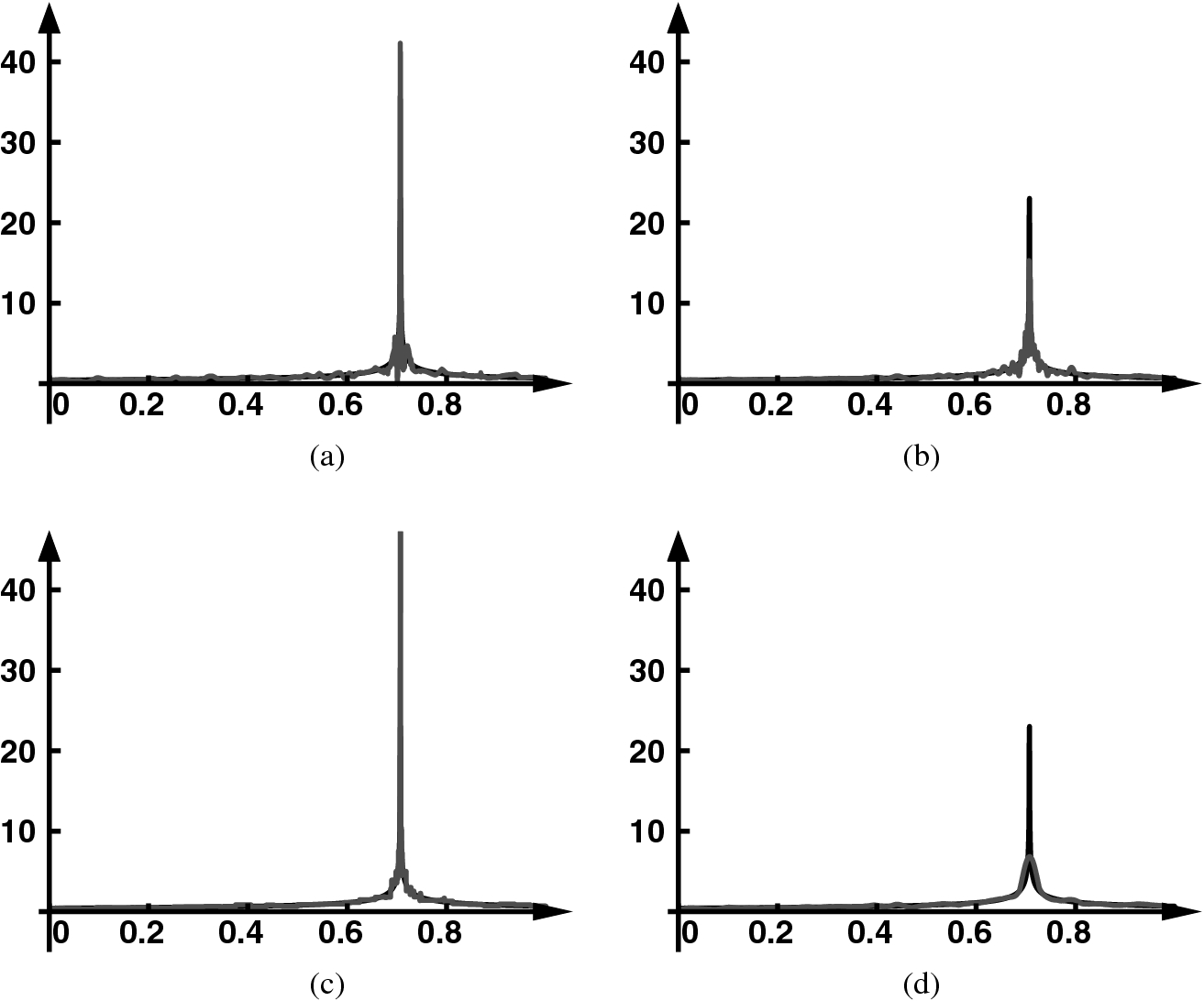
Panel (a): power law and its estimation from  observations using the MLPT procedure of this paper. Panel (b): estimation from the same observations using a probit transform centered around the location of the singularity, thus hinges on the knowledge of this location. Panel (c): estimation using the finest possible Haar wavelet transform. This transform involves full processing of many resolution levels. Panel (d): estimation using straightforward uniscale kernel density estimation
observations using the MLPT procedure of this paper. Panel (b): estimation from the same observations using a probit transform centered around the location of the singularity, thus hinges on the knowledge of this location. Panel (c): estimation using the finest possible Haar wavelet transform. This transform involves full processing of many resolution levels. Panel (d): estimation using straightforward uniscale kernel density estimation
6 Illustration and Concluding Discussion
Ongoing research concentrates on motivating choices for the tuning parameters in the proposed data transformation and processing. In particular, the data transformation depends on the choice of the finest resolution bandwidth  , the degree of the local polynomial in the prediction step, the precise design of the updated step. Also, the Unbalanced Haar prefilter is parametrized by a fine scale
, the degree of the local polynomial in the prediction step, the precise design of the updated step. Also, the Unbalanced Haar prefilter is parametrized by a fine scale  . Processing parameters include the threshold value, which is selected using the AIC approach of Sect. 5, and the sizes of the blocks in the block threshold procedure.
. Processing parameters include the threshold value, which is selected using the AIC approach of Sect. 5, and the sizes of the blocks in the block threshold procedure.
For the result in Fig. 2, the MLPT adopted a local linear prediction step. In the wavelet literature, the transform is said to have two dual vanishing moments, i.e.,  , meaning that all detail coefficients of a linear function are zero. The MLPT for the figure also includes an update step designed for two primal vanishing moments, meaning that
, meaning that all detail coefficients of a linear function are zero. The MLPT for the figure also includes an update step designed for two primal vanishing moments, meaning that  for
for  and
and  . Block sizes were set to one, i.e., classical thresholding was used.
. Block sizes were set to one, i.e., classical thresholding was used.
The density function in the simulation study is the power law  on the finite interval [0, 1], with a singular point
on the finite interval [0, 1], with a singular point  in this simulation study and
in this simulation study and  . The sample size is
. The sample size is  . The MLPT approach, unaware of the presence and location of
. The MLPT approach, unaware of the presence and location of  , is compared with a kernel density estimation applied to a probit transform of the observations,
, is compared with a kernel density estimation applied to a probit transform of the observations,  for
for  and
and  for
for  . This transform uses the information on the singularity’s location, in order to create a random variable whose density has no end points of a finite interval, nor any singular points inside. In this experiment, the MLPT outperforms the Probit transformed kernel estimation, both in the reconstruction of the singular peak and in the reduction of the oscillations next to the peak. With the current procedure, this is not always the case. Further research concentrates on the design making the MLPT analyses as close as possible to orthogonal projections, using appropriate update steps. With an analysis close to orthogonal projection, the variance propagation throughout the analysis, processing, and reconstruction can be more easily controlled, thereby reducing spurious effects in the reconstruction. Both MLPT and Probit transformation outperform a straightforward uniscale kernel density estimation. This estimation, illustrated the Fig. 2d, oversmooths the sharp peaks of the true density.
. This transform uses the information on the singularity’s location, in order to create a random variable whose density has no end points of a finite interval, nor any singular points inside. In this experiment, the MLPT outperforms the Probit transformed kernel estimation, both in the reconstruction of the singular peak and in the reduction of the oscillations next to the peak. With the current procedure, this is not always the case. Further research concentrates on the design making the MLPT analyses as close as possible to orthogonal projections, using appropriate update steps. With an analysis close to orthogonal projection, the variance propagation throughout the analysis, processing, and reconstruction can be more easily controlled, thereby reducing spurious effects in the reconstruction. Both MLPT and Probit transformation outperform a straightforward uniscale kernel density estimation. This estimation, illustrated the Fig. 2d, oversmooths the sharp peaks of the true density.