© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_28

Interval-Wise Testing of Functional Data Defined on Two-dimensional Domains

Patrick B. Langthaler1  , Alessia Pini2   and Arne C. Bathke1  
(1)
Department of Mathematics, Paris-Lodron University Salzburg, Hellbrunnerstraße 34, 5020 Salzburg, Austria
(2)
Department of Statistical Sciences, Università Cattolica del Sacro Cuore, Largo A. Gemelli, 1-20123 Milan, Italy
 
 
Patrick B. Langthaler (Corresponding author)
Email: PatrickBenjamin.Langthaler@stud.sbg.ac.at
 
Alessia Pini
Email: alessia.pini@unicatt.it
 
Arne C. Bathke
Email: arne.bathke@sbg.ac.at

Abstract

Functional Data Analysis is the statistical analysis of data sets composed of functions of a continuous variable on a given domain. Previous work in this area focuses on one-dimensional domains. In this work, we extend a method developed for the one-dimensional case, the interval-wise testing procedure (IWT), to the case of a two-dimensional domain. We first briefly explain the theory of the IWT for the one-dimensional case, followed by a proposed extension to the two-dimensional case. We also discuss challenges that appear in the two-dimensional case but do not exist in the one-dimensional case. Finally, we provide results of a simulation study to explore the properties of the new procedure in more detail.

Keywords
Functional Data AnalysisType I Error ControlRectangular Domain

1 Introduction

Functional Data Analysis is the statistical analysis of data sets composed of functions of a continuous variable (time, space, ...), observed in a given domain (see Ramsay and Silverman [8]). In this work, we focus on the inference for functional data, a particularly challenging problem since functional data are objects embedded in infinite-dimensional spaces, and the traditional inferential tools cannot be used in this case. The challenge of deriving inference for functional data is currently tackled by literature from two different perspectives: global inference involves testing a (typically simple) null hypothesis against an alternative extending over the whole (remaining) domain of the parameter space (see e.g. Benko et al. [1], Cuevas et al. [2], Hall and Keilegom [4], Horváth et al. [5], Horváth and Kokoszka [5]); local inference instead addresses the problem of selecting the areas of the domain responsible for the rejection of the null hypothesis, assigning a p-value to each point of the domain (see e.g. Pini and Vantini [6, 7]).

Here, we take the second line of research as a starting point. More precisely, Pini and Vantini [6] suggest performing inference on the coefficients of a B-spline basis expansion, while in extension of the previous work, the same authors propose the interval-wise testing procedure (IWT) which performs inference directly on the functional data (without requiring a basis expansion) [7]. Both methods propose to adjust local p-values in order to control the interval-wise error rate, that is, the probability of wrongly rejecting the null hypothesis in any interval.

In this paper, we extend the IWT to functional data defined in two-dimensional domains. Indeed, all current works addressing local inference deal with one-dimensional domains. Their extension to two (or more) dimensions is not trivial since it would require to define a proper notion of ‘interval’ in two dimensions. We start from a brief overview of the IWT and its properties (Sect. 2, then we discuss how to extend this approach to two-dimensional domains (Sect. 3). Finally, we report in Sect. 4 on a simulation study investigating the properties of this new method, and draw some conclusions (Sect. 5).

2 Previous Works: The IWT for Functional Data Defined on One-Dimensional Domains

We give here a brief overview of the IWT. For a thorough treatment of the method, see Pini and Vantini [6, 7]. The setting in which the IWT can be used is this: assume that for each unit of analysis (a subject, mechanical object, etc.) we have observed a function $$x_i(t)$$, $$i=1,\ldots ,N$$, $$t \in D = [a,b]$$, with $$a,b \in \mathbb R$$. For ease of notation, we assume here that functional data are continuous. However, this assumption can be relaxed (see Pini and Vantini [7]).

Assume that we aim at locally testing, for each point of the domain, a null hypothesis $$H_0^t$$ against an alternative $$H_1^t$$. For example, assume that the sample is divided into a different groups. We indicate our functional data as $$x_{ij}(t)$$, where $$j=1,\ldots ,a$$ denotes the group, and $$i=1,\ldots ,n_j$$ denotes the units in group j. We could be interested in testing mean differences between the groups:
$$\begin{aligned} H_0^t:\, \mu _1{(t)} = \mu _2{(t)} = \cdots =\mu _a{(t)}, \quad H_1^t = H_0^C, \end{aligned}$$
(1)
where $$\mu _j{(t)} = \mathbb E [x_{ij}(t)]$$. Testing each hypothesis (1) is straightforward since it involves univariate data. The challenge is to adjust the results in order to take the multiplicity of tests into account. The IWT executes this as follows: First, we test each hypothesis (1) separately, and denote the corresponding p-value as p(t). This is an unadjusted p-value function defined for all $$t\in D$$. Next, we test the null and alternative hypotheses over each interval $$\mathscr {I} = [t_1,t_2] \subseteq D$$ and the complementary set of each interval $$\mathscr {I}^C = D \setminus \mathscr {I}$$:
$$\begin{aligned} H_0^{(\mathscr {I})}&:\, \bigcap _{t \in \mathscr {I}} H_0^{(t)} : \, \mu _1{(t)} = \mu _2{(t)} = ... =\mu _a{(t)} \; \forall t \in \mathscr {I}; \; H_1^{(\mathscr {I})} = H_0^{(\mathscr {I})^C}; \end{aligned}$$
(2)
$$\begin{aligned} H_0^{(\mathscr {I}^C)}&:\, \bigcap _{t \in \mathscr {I}^C} H_0^{(t)} : \, \mu _1{(t)} = \mu _2{(t)} = ... =\mu _a{(t)} \; \forall t \in \mathscr {I}^C; \; H_1^{(\mathscr {I}^C)} = H_0^{(\mathscr {I}^C)^C}. \end{aligned}$$
(3)
Denote the p-values of test (2) and (3) as $$p^{\mathscr {I}}$$ and $$p^{\mathscr {I}^C}$$, respectively.
For each point $$t\in D$$, we now define an adjusted p-value for interval-wise testing as the maximum p-value of all tests including the point t:
$$\begin{aligned} \widetilde{p}_{IWT}(t) := \max \left\{ \max _{\mathscr {I} : t\in \mathscr {I}} p^\mathscr {I} ; \max _{\mathscr {I}^C : t\in \mathscr {I}^C} p^{\mathscr {I}^C} \right\} . \end{aligned}$$
(4)
These p-values provide interval-wise control of the type 1 error rate, that is,
$$\begin{aligned} \forall \alpha \in (0,1):\, \forall \mathscr {I}:\, P_{H_0^{\mathscr {I}}}\left( \bigcup _{t \in \mathscr {I}} \{\widetilde{p}_{IWT}(t) \le \alpha \}\right) \le \alpha . \end{aligned}$$
In practice, it is obviously not possible to perform a statistical test in every point of the domain, and in every interval and complementary interval. So, the implementation of the IWT requires discretizing functional data on a dense grid of p equally sized subintervals. Functional data are approximated with a constant in each subinterval. Then, the unadjusted p-value is computed on each subinterval, and the p-value of tests (2) and (3) is computed for every interval and the complementary interval that can be created as a union of the p subintervals. Finally, the adjusted p-value $$\widetilde{p}_{IWT}(t)$$ is computed applying formula (4) on the performed tests. For details, see Pini and Vantini [7].

3 Methods

The primary task in extending the IWT to functional data defined on two-dimensional domains is to find a suitable neighbourhood over which the tests are performed (corresponding to the intervals in the one-dimensional case). If one has decided on a neighbourhood, the very same principle of p-value adjustment as in the one-dimensional case applies. Instead of interval-wise control, we then get control for every neighbourhood of the specified type. What constitutes a good neighbourhood can depend on the specific data one wants to analyse. If there is reason to believe that the two-dimensional subset of the domain in which there is a significant difference between groups takes on a certain shape, then it is reasonable to take this kind of shape as the neighbourhood. The choice of neighbourhood might also depend on the shape of the domain of the functional data. In this contribution, we will try to stay as general as possible and make no assumptions about the area in which significant differences may be found. We do however have to make an assumption about the shape of the two-dimensional domain. We will assume that the data have been recorded on a rectangular grid. This shape makes the use of rectangles or squares as neighbourhoods plausible.

Before we continue, we would like to make one important remark: When using intervals as neighbourhoods in the one-dimensional case, the complement of an interval can be seen as an interval that wraps around. When using rectangles or squares in the two-dimensional scenario, this is not the case. A rectangle that leaves the domain on the right or top and comes in on the left or bottom can not necessarily be described as the complementary set of a rectangle fully contained in the domain. For ease of computation, we decided to test for all possible squares and the complements thereof and to not test squares that wrap around.

Here, we describe the extension of IWT to the two-dimensional domain D, starting from a general definition of neighbourhood. In the following subsection, we discuss instead different possible choices of neighbourhoods.

3.1 The Extension of the IWT to Functional Data Defined on Two-Dimensional Domains

Assume to observe functional data $$x_{i}(t)$$, with $$t\in D=[a_1,b_1]\times [a_2,b_2]$$, and $$i=1,\ldots ,n$$. Assume that the functions $$x_{i}(t)$$ are continuous on D. Also, in this case, we aim at locally testing a null hypothesis against an alternative, and selecting the points of the domain where the null hypothesis is rejected. For instance, assume again that units belong to a groups, and that we aim at testing mean equality between the groups (1).

The two-dimensional extension of the IWT requires defining a notion of ‘interval’ in two dimensions, or neighbourhood. Let us assume that a proper family of neighbourhoods has been defined (e.g. all rectangles and rectangles’ complements included in the domain), and denote as $$\mathscr {N}$$ a generic neighbourhood. Then, the two-dimensional IWT requires testing the null and alternative hypotheses on every possible neighbourhood, and on every complement of it, i.e. performing the tests
$$\begin{aligned} H_0^{(\mathscr {N})}&:\, \bigcap _{t \in \mathscr {N}} H_0^{(t)} : \, \mu _1{(t)} = \mu _2{(t)} = \cdots =\mu _a{(t)} \; \forall t \in \mathscr {N}; \; H_1^{(\mathscr {N})} = H_0^{(\mathscr {N})^C}; \end{aligned}$$
(5)
$$\begin{aligned} H_0^{(\mathscr {N}^C)}&:\, \bigcap _{t \in \mathscr {N}^C} H_0^{(t)} : \, \mu _1{(t)} = \mu _2{(t)} = ... =\mu _a{(t)} \; \forall t \in \mathscr {N}^C; \; H_1^{(\mathscr {N}^C)} = H_0^{(\mathscr {N}^C)^C} \end{aligned}$$
(6)
for all $$\mathscr {N} \in \mathscr {F}$$. Let us denote with $$p^{\mathscr {N}}$$ the p-value of such test. Then, the adjusted p-value at point $$t\in D$$ can be computed as
$$\begin{aligned} \widetilde{p}_{IWT} (t) := \max \left\{ \max _{\mathscr {N} : t \in \mathscr {N}}p^{\mathscr {N}} ; \max _{\mathscr {N}^C : t \in \mathscr {N}}p^{\mathscr {N}} \right\} . \end{aligned}$$
(7)
It is then straightforward to prove, extending the result of IWT for one-dimensional data, that such p-values provide interval-wise control of the type 1 error rate over all neighbourhoods, that is,
$$\begin{aligned} \forall \alpha \in (0,1):\, \forall \mathscr {N}:\, P_{H_0^{\mathscr {N}}}\left( \bigcup _{t \in \mathscr {N}} \{\widetilde{p}_{IWT}(t) \le \alpha \}\right) \le \alpha . \end{aligned}$$

3.2 The Problem of Dimensionality in the Choice of the Neighbourhood

In the one-dimensional case, we have two parameters that fully characterise an interval: the starting point of the interval and its length. There are p different starting points and p different lengths. There is, however, only one interval of length p, giving us a total of $$p^2 - p + 1$$ possible intervals for which p-values need to be computed. Thus, the computational cost is of order $$p^2$$. If we want to use rectangles as neighbourhoods in the two-dimensional case, we can first freely chose the lower left corner of the rectangle, giving us $$p_1 p_2$$ possibilities, where $$p_1$$ is the number of grid points on the x-axis and $$p_2$$ is the number of grid points on the y-axis. Once the lower left corner is chosen, the rectangle can then be fully characterised by its length in the x-direction and its length in the y-direction. These can however not be chosen freely since the rectangle has to remain inside the domain. Overall, this puts us as $$\frac{p_1(p_1-1)p_2(p_2-1)}{2}$$ possible neighbourhoods, setting the computational cost to the order of $$p_{1}^{2}p_{2}^{2}$$.

If we are content with only using squares, assuming for now that the domain D is observed on a square grid discretised in $$p \times p$$ points, we only need to test for $$\frac{p(p-1)(2p-1)}{6}$$ neighbourhoods. The computational cost is thus of the order $$p^3$$, an order lower than the one of the rectangle case.

What if we want to have the benefit of lower computational cost but our domain is a rectangular grid? In this case, we can simply rescale the grid: assume we start from a $$p_1 \times p_2$$ grid and assume $$p_1 \ne p_2$$. We fix $$p := \min \{p_1,p_2\}$$. Let, w.l.o.g, $$p_1 < p_2$$. We then rescale the axis with the $$p_2$$ observations by using new points with coordinates $$a_2 + \frac{i(b_2 - a_2)}{p-1}$$, $$i=0,...,p-1$$. If $$\frac{p_2 - 1}{p_1 - 1}$$ is not an integer, then the functions were not observed at the resulting new grid points. We can however use a simple nearest neighbour imputation, using only the nearest neighbour. Note that when we speak of squares and rectangles, we mean in terms of the grid, not in terms of the physical units of the observations. Accordingly, by the nearest neighbour, we mean the nearest observation, assuming that the distance between two adjacent grid points is the same for the two dimensions. Our squares thus can be thought of as rectangles whose sides have the same ratio as the sides of the original domain.

4 Simulation Study

We chose to conduct a simulation study looking at the following scenarios:

  • (S0) The grid is quadratic and the null hypothesis is true everywhere. In this case, we should see that we have weak control of the error rate.

  • (S1) The grid is quadratic and the null hypothesis is violated on a square region. In this case, we should have our square-wise control of the error rate.

  • (S2) The grid is quadratic and the null hypothesis is violated on a region that is not a square but a rectangle with unequal sides. Thus, we have no control of the FWER in this scenario.

  • (S3) The grid is rectangular and the null hypothesis is violated on a rectangular region, the ratio of the sides of which is the same as the ratio of the sides of the grid. If our rescaling works as is should, we should see the same results as in (S1).

4.1 Simulation Settings

For all our simulation scenarios, we followed the following scheme: First, we created two mean functions on some domain. We discretised the mean functions by evaluating them on a grid. We created observations by adding a realisation of a random variable
$$\begin{aligned} y = (y_{1,1}, y_{1,2}, \ldots , y_{1,p_{2}}, y_{2,1}, \ldots , y_{p_{1},1}, \ldots , y_{p_{1},p_{2}}) \end{aligned}$$
(8)
to each mean grid. This realisation was drawn from a multivariate Gaussian distribution with mean zero and covariance function
$$\begin{aligned} Cov(Y_{i,j}, Y_{i',j'}) = 0.1 \cdot e^{-10((i-i')^2 + (j-j')^2)}. \end{aligned}$$
(9)
This simulates data that come from an infinitely differentiable stochastic process (see Ramussen and Williams [9] pp. 83). Between subjects and groups, the errors were uncorrelated. We did this 10 times for the first mean function and 10 times for the second, giving us a sample of 20 observations divided into two groups. The hypothesis of interest was the equality of distribution between the two groups, and the specific test used was a permutation test by Hall and Tajvidi [3]. In scenarios (S0), (S1) and (S2), the domain was the square $$[0,1] \times [0,1]$$. In (S3), the domain was $$[0,2] \times [0,1]$$. The first mean function was always a constant zero. The second mean function was as follows:

  • (S0) The second mean function was also a constant zero.

  • (S1) The second mean function was defined as
    $$ f(x,y) = {\left\{ \begin{array}{ll} 0 &{}\text { if } x \le 0.25 \text { or } x \ge 0.75 \text { or } y \le 0.25 \text { or } y \ge 0.75 \\ \frac{x - 0.25}{0.25} &{}\text { if } 0.25< x \le 0.5 \text { and } x \le y \le 1-x \\ \frac{0.75 - x}{0.25} &{}\text { if } 0.5< x< 0.75 \text { and } x \le y \le 1-x \\ \frac{y - 0.25}{0.25} &{}\text { if } 0.25< y \le 0.5 \text { and } y \le x \le 1-y \\ \frac{0.75 - y}{0.25} &{}\text { if } 0.5< y < 0.75 \text { and } \le x \le 1-y \end{array}\right. } $$
    This is a quadratic pyramid of height 1 and with base $$[0.25,0.75] \times [0.25,0.75]$$.
  • (S2) The second mean function was defined as
    $$ f(x,y) = {\left\{ \begin{array}{ll} 0 &{}\text { if } y \le 0.25 \text { or } y \ge 0.75 \\ \frac{y - 0.25}{0.25} &{}\text { if } 0.25< y \le 0.5 \\ \frac{0.75 - y}{0.25} &{}\text { if } 0.5< y < 0.75 \end{array}\right. } $$
    This is a triangular prism of height 1 and with base $$[0,1] \times [0.25,0.75]$$.
  • (S3) The second mean function was defined as
    $$ f(x,y) = {\left\{ \begin{array}{ll} 0 &{}\text { if } x \le 0.5 \text { or } x \ge 1.5 \text { or } y \le 0.25 \text { or } y \ge 0.75 \\ 2x - 1 &{}\text { if } 0.5< x \le 1 \text { and } 0.5x \le y \le 1-0.5x \\ 3 - 2x &{}\text { if } 1< x< 1.5 \text { and } 0.5x \le y \le 1-0.5x \\ \frac{y - 0.25}{0.25} &{}\text { if } 0.25< y \le 0.5 \text { and } 2y \le x \le 2-2y \\ \frac{0.75 - y}{0.25} &{}\text { if } 0.5< y < 0.75 \text { and } 2y \le x \le 2-2y \end{array}\right. } $$
    This is a pyramid of height 1 with base $$[0.5,1.5] \times [0.25,0.75]$$.
As to the number of grid points, we used $$21 \times 21$$ grid points in scenarios (S0), (S1) and (S2), and $$41 \times 21$$ grid points in scenario (S3). The mean functions for the second group for the scenarios (S1), (S2) and (S3) are illustrated in Figure 1
../images/461444_1_En_28_Chapter/461444_1_En_28_Fig1_HTML.png
Fig. 1

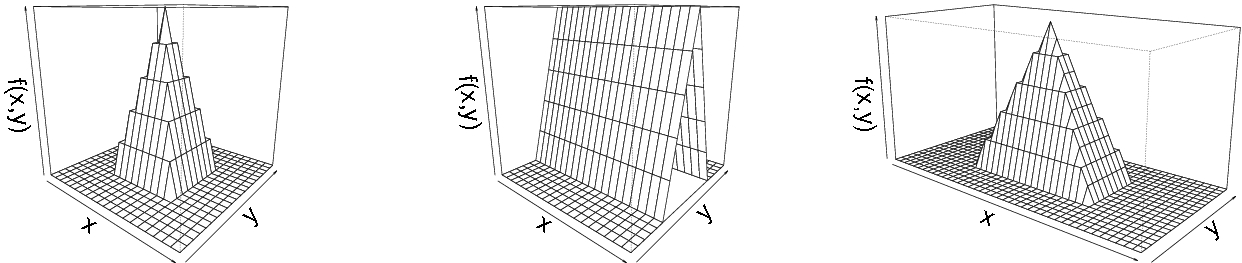
Perspective plots of the mean functions used in scenarios (S1), (S2) and (S3) (from left to right)

4.2 Results of Simulation Study

For each scenario, we estimated the FWER of the IWT and the pointwise probability of rejection over 1000 simulation runs. The nominal FWER level was set to $$\alpha =0.05$$. The estimated FWER is reported in Table 1, and the probability of rejection in Fig. 2. Since the estimated probability of rejection was zero in all points in (S0), we decided to show in the figure only the results of (S1), (S2) and (S3). Looking at the FWER, the simulations confirmed what was expected from the theory. When the null hypothesis was true over the whole domain (S0) when it was violated on a square (S1), and when it was violated on a rectangle with the same aspect ratio as the domain (S3), the FWER was controlled, and in fact, the procedure was conservative (the actual FWER was significantly lower than its nominal value in all three cases). However, when the null hypothesis was violated on a region that was different from a square (S2), the FWER was not controlled. Indeed, in this scenario, it was slightly higher than its nominal level.
Table 1

FWER estimated over 1000 runs in scenarios (S0), (S1), (S2) and (S3)

 

Scenario 0

Scenario 1

Scenario 2

Scenario 3

FWER

0.014

0.021

0.21

0.032

Regarding the power, we can see that the two-dimensional IWT was able to correctly detect the portions of the domain where the null hypothesis was false with a reasonably good power (see Figure 2). As expected, the power was relatively low at the boundary between the region where the null hypothesis was true and the region where it was false, but it reached the value 1 inside the latter region.
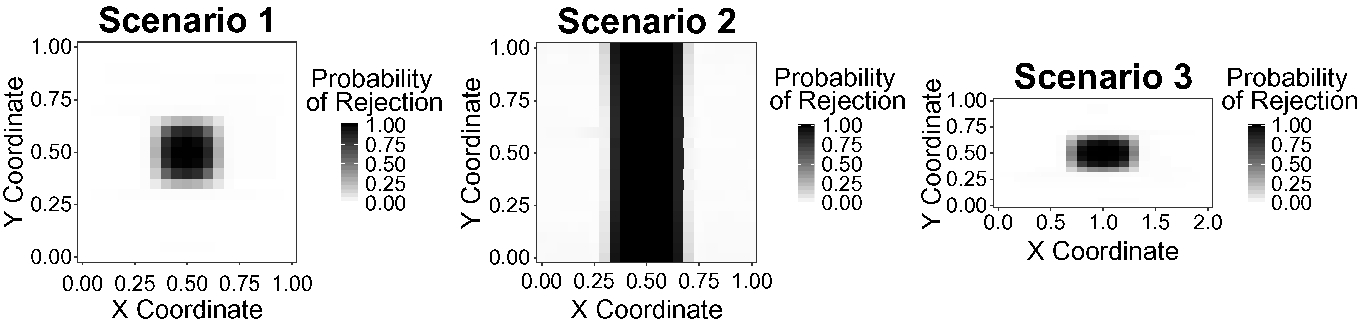
../images/461444_1_En_28_Chapter/461444_1_En_28_Fig2_HTML.png
Fig. 2

Probability of rejection of each grid point estimated over 1000 runs in scenarios (S1), (S2) and (S3) (from left to right)

5 Discussion

In this paper, we extended the IWT by Pini and Vantini [7] to two-dimensional functional data defined on a rectangular domain. We performed a simulation study to assess the performance of the method when using squares and/or rectangles with the same ratio of sides as the domain and the complement of such shapes as neighbourhoods. The results of the simulation study show that the FWER is controlled when the null hypothesis is true in such neighbourhoods, but not necessarily when it is true on neighbourhoods of a different shape. The simulation also shows that the method can be quite conservative in some instances. Future work will target further improving the respective performance of the method in these situations while keeping the computational complexity manageable.

Acknowledgements

The presented research was funded by the Austrian Science Fund (FWF): KLI657-B31 and I 2697-N31 and by PMU-FFF: A-18/01/029-HÖL.