© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_32

Correction for Optimisation Bias in Structured Sparse High-Dimensional Variable Selection

Bastien Marquis1   and Maarten Jansen1  
(1)
Universit libre de Bruxelles, Brussels, Belgium
 
 
Bastien Marquis (Corresponding author)
Email: bastien.marquis@ulb.ac.be
 
Maarten Jansen
Email: maarten.jansen@ulb.ac.be

Abstract

In sparse high-dimensional data, the selection of a model can lead to an overestimation of the number of nonzero variables. Indeed, the use of an $$\ell _1$$ norm constraint while minimising the sum of squared residuals tempers the effects of false positives, thus they are more likely to be included in the model. On the other hand, an $$\ell _0$$ regularisation is a non-convex problem and finding its solution is a combinatorial challenge which becomes unfeasible for more than 50 variables. To overcome this situation, one can perform selection via an $$\ell _1$$ penalisation but estimate the selected components without shrinkage. This leads to an additional bias in the optimisation of an information criterion over the model size. Used as a stopping rule, this IC must be modified to take into account the deviation of the estimation with and without shrinkage. By looking into the difference between the prediction error and the expected Mallows’s Cp, previous work has analysed a correction for the optimisation bias and an expression can be found for a signal-plus-noise model given some assumptions. A focus on structured models, in particular, grouped variables, shows similar results, though the bias is noticeably reduced.

1 Introduction

This paper falls under the scope of variable selection in high-dimensional data. The number of variables might then be larger than the number of observations, thus leading to difficulties in the computation of the models. Indeed, the classical tools for low-dimensional data can no longer be used. In order to find a solution, the assumption of sparsity is often made, meaning that the number of nonzero variables is supposed to be smaller than the number of observations. Besides an improvement in calculations, another benefit from sparsity results from the fact that the obtained models are more interpretable. Finding the nonzeros becomes the main objective. The obvious method would be to test all subsets; however, this proves to be unfeasible for more than a few dozen variables. More greedy algorithms exist, such as forward selection or backward elimination, but they are likely to miss the true model in addition to remaining computationally heavy. An other way to tackle the problem is to use regularisation on the sum of squared residuals. For a linear model $$\mathbf {Y} = \mathbf {X}\mathbf {\beta } + \mathbf {\varepsilon }$$ with $$\mathbf {Y}, \mathbf {\varepsilon } \in \mathrm{I\!R}^n$$ and $$\mathbf {\beta } \in \mathrm{I\!R}^m$$, this consists in finding the estimator $$\widehat{\mathbf {\beta }}$$ that solves an equation usually of the form:
$$\begin{aligned} \min _{\mathbf {\beta }} \frac{1}{n} \Vert \mathbf {Y}-\mathbf {X}\mathbf {\beta }\Vert ^2_2 + \lambda \Vert \mathbf {\beta }\Vert ^p_p, \end{aligned}$$
where the regularisation parameter $$\lambda $$ is a kind of ‘budget’: acting as a weight, it limits the norm of $$\widehat{\mathbf {\beta }}$$. Ridge regression and Lasso are special cases where $$p = 2$$ and $$p = 1$$, respectively, and their solutions can be calculated even when $$\mathbf {X}$$ is not of full rank.

Ideally, one would perform $$\ell _0$$ regularisation, i.e. penalising the sum of squared residuals by the number of nonzero variables, but this is a combinatorial problem, and therefore intractable from the computational point of view. On the other hand, Lasso [8] and other $$\ell _1$$-type regularisations (penalisation by the sum of the absolute values of the selected variables) offer a quadratic programming alternative whose solution is still a proper variable selection, as it contains many zeros.

Lasso has many advantages. First, it applies shrinkage on the variables which can lead to better predictions than simple least squares due to Stein’s phenomenon [7]. Second, the convexity of its penalty means Lasso can be solved numerically. Third, $$\ell _1$$ regularisation is variable selection consistent under certain conditions, provided that the coefficients of the true model are large enough compared to the regularisation parameter [6, 10, 14]. Fourth, Lasso can take into account structures; simple modifications of its penalisation term result in structured variable selection. Such variations among others are the fused lasso [9], the graphical lasso [3] and the composite absolute penalties [13] including the group-lasso [12]. Fifth, for a fixed regularisation parameter, $$\ell _1$$ regularisation has nearly the same sparsity as $$\ell _0$$ regularisation [2]. However, this does not hold anymore when the regularisation parameter is optimised in a data-dependent way, using an information criterion such as AIC [1] or Mallows’s Cp [5].

Mallows’s Cp, like many other information criteria, takes the form of a penalised—likelihood or—sum of squared residuals whose penalty depends on the number of selected variables. Therefore, among all models of equal size, the selection is based on the sum of squared residuals. Because of sparsity, it is easy to find a well-chosen combination of falsely significant variables that reduces the sum of squared residuals, by fitting the observational errors. The effects of these false positives can be tempered by applying shrinkage. The optimisation of the information criterion then overestimates the number of variables needed, including too many false positives in the model. In order to avoid this scenario, one idea could be to combine both $$\ell _1$$ and $$\ell _0$$ regularisation: the former to select the nonzeros and the latter to estimate their value. The optimal balance between the sum of squared residuals and the $$\ell _0$$ regularisation should shift towards smaller models. Of course, this change must be taken into account and the expression of the information criterion consequently adapted. The correction for the difference between $$\ell _0$$ and $$\ell _1$$ regularisation has been described as a ‘mirror’ effect [4].

In Sect. 2, we explain more the mirror effect. The main contribution of this paper follows and concerns the impact of a structure among the variables and how it affects the selection. More precisely, the behaviour of the mirror effect for unstructured and structured signal-plus-noise models is investigated in Sect. 3. A simulation is presented in Sect. 4 to support the previous sections.

2 The Mirror Effect

Consider the linear model
$$\mathbf {Y} = \mathbf {X}\mathbf {\beta } + \mathbf {\varepsilon }$$
where $$\mathbf {\varepsilon }$$ is a n-vector of independent and identically distributed errors with $$E(\varepsilon _i) = 0$$ and $$\mathrm {var}(\varepsilon _i) = \sigma ^2$$ for $$i = 1,\ldots ,n$$. The design matrix $$\mathbf {X}$$ has size $$n \times m$$ with n possibly smaller than m. We assume $$\mathbf {\beta } \in \mathrm{I\!R}^m$$ is sparse in the sense that the unknown number of nonzeros $$n_1$$ in $$\mathbf {\beta }$$ is smaller than n. For a given k, let $$\mathbf {S}^k$$ be a binary m-vector with $$m-k$$ zeros, provided by a procedure $$\mathcal {S}(\mathbf {Y},k)$$ which can be unstructured best k selection or any structured procedure. An example of such a procedure could be an implementation of Lasso with the regularisation parameter fine-tuned to obtain the appropriate model size. Also, define $$\mathbf {O}^k$$ as the selection found by an oracle knowing $$\mathbf {X}\mathbf {\beta }$$ without noise, using the same procedure as for $$\mathbf {S}^k$$, i.e. $$\mathbf {O}^k = \mathcal {S}(\mathbf {X}\mathbf {\beta },k)$$. The notations $$\mathbf {X}_{\mathbf {S}^k}$$ and $$\mathbf {X}_{\mathbf {O}^k}$$ are used for the $$n \times k$$ submatrices of $$\mathbf {X}$$ containing the k columns corresponding to the 1s in $$\mathbf {S}^k$$ and $$\mathbf {O}^k$$, respectively.
One way to look at the mirror effect comes from investigating the difference between the expected average squared prediction error and Mallows’s Cp criterion1. The quality of the oracle least squares projection, $$\widehat{\mathbf {\beta }}_{\mathbf {O}^k} = (\mathbf {X}^T_{\mathbf {O}^k}\mathbf {X}_{\mathbf {O}^k})^{-1} \mathbf {X}^T_{\mathbf {O}^k}\mathbf {Y}$$, is measured by the prediction error $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {O}^k})$$ which can be, in turn, estimated unbiasedly by $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {O}^k})$$, where, for a generic selection $$\mathbf {S}$$,
$$\begin{aligned} \mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}}) = \frac{1}{n}E\left( \Vert \mathbf {X}\mathbf {\beta } - \mathbf {X}_{\mathbf {S}}\widehat{\mathbf {\beta }}_{\mathbf {S}}\Vert ^2_2\right) \end{aligned}$$
(1)
and $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}})$$ is a non-studentised version of Mallows’s Cp
$$\begin{aligned} \Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}}) = \frac{1}{n}\Vert \mathbf {Y} - \mathbf {X}_{\mathbf {S}}\widehat{\mathbf {\beta }}_{\mathbf {S}}\Vert ^2_2 + \frac{2|\mathbf {S}|}{n}\sigma ^2 - \sigma ^2. \end{aligned}$$
(2)
The selection $$\mathbf {S}^k = \mathcal {S}(\mathbf {Y},k)$$, however, depends on $$\mathbf {Y}$$. Hence, for the corresponding least squares projection $$\widehat{\mathbf {\beta }}_{\mathbf {S}^k} = (\mathbf {X}^T_{\mathbf {S}^k}\mathbf {X}_{\mathbf {S}^k})^{-1} \mathbf {X}^T_{\mathbf {S}^k}\mathbf {Y}$$, the expectation of $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ will not be equal to $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$.

Among all selections of size k for k large enough so that the important variables are in the model, the procedure consisting of minimising (2), i.e. $$\mathcal {S}(\mathbf {Y},k) = \mathrm {arg}\min _{|\mathbf {S}|=k} \Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}})$$, adds seemingly nonzero variables—that should, in fact, be zeros—in order to fit the observational errors by minimising further the distance between $$\mathbf {X}_{\mathbf {S}^k}\widehat{\mathbf {\beta }}_{\mathbf {S}^k}$$ and $$\mathbf {Y}$$. The consequence is a better-than-average appearance of $$E\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ contrasting with the worse-than-average true prediction error: indeed the false positives perform worse in staying close to the signal without the errors than variables selected in a purely arbitrary way. This two-sided effect of appearance versus reality is described as a mirror effect [4].

Whereas information criteria have been designed to evaluate the quality of one specific model, the optimisation over the randomised $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ affects the statistics of the selected variables. Because the selection $$\mathbf {O}^k$$ does not depend on $$\mathbf {Y}$$, leaving the statistics of the selected variables unchanged, the oracle curve $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {O}^k})$$ acts as a mirror reflecting $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ onto $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$:
$$\begin{aligned} \mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k}) - \mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {O}^k}) \approx m_k \approx \mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {O}^k}) - E\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k}). \end{aligned}$$
(3)
Figure 1 plots $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ and $$\Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ in dashed and dotted lines, respectively, as functions of the model size k. Also, the mirror curve $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {O}^k}) \approx \Delta _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k}) + m_k$$ is represented as the solid curve. Details of the calculations can be found in Sect. 4.
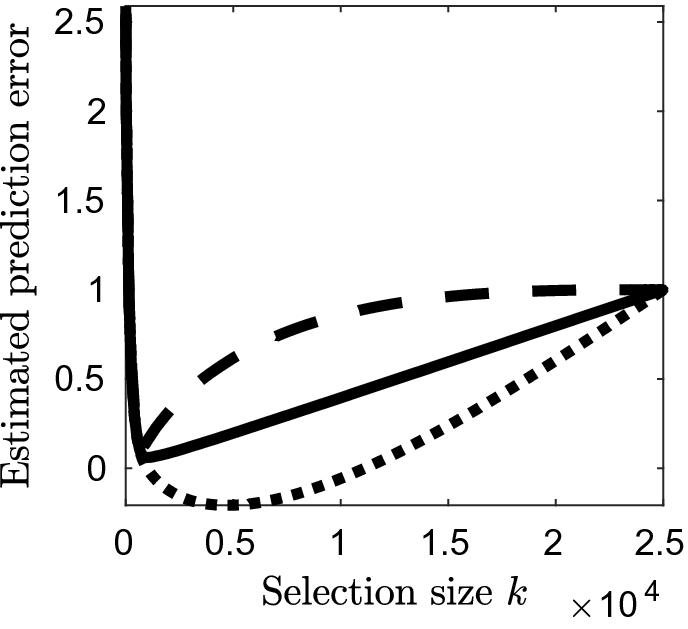
../images/461444_1_En_32_Chapter/461444_1_En_32_Fig1_HTML.png
Fig. 1

Illustration of the mirror effect. The mirror curve is plotted in solid line as a function of the model size and reflects the prediction error and Mallows’s Cp, represented as dashed and dotted curves, respectively

The Mirror and Degrees of Freedom
The mirror effect is closely related to the concept of generalised degrees of freedom [11]. Defining the residual vector $$\mathbf {e}_k = \mathbf {Y}-\mathbf {X}_{\mathbf {S}^k}\widehat{\mathbf {\beta }}_{\mathbf {S}^k}$$, the generalised degrees of freedom are given by
$$\begin{aligned} \nu _k = \frac{1}{\sigma ^2} E[\mathbf {\varepsilon }^T(\mathbf {\varepsilon }-\mathbf {e}_k)] = \frac{1}{n} E(\mathbf {\varepsilon }^T \mathbf {X}_{\mathbf {S}^k}\widehat{\mathbf {\beta }}_{\mathbf {S}^k}) \end{aligned}$$
(4)
and $$\Lambda _p(\widehat{\mathbf {\beta }}_{\mathbf {S}^k}) = n^{-1} \Vert \mathbf {Y}-\mathbf {X}_{\mathbf {S}^k}\widehat{\mathbf {\beta }}_{\mathbf {S}^k}\Vert ^2_2 + 2\nu _k n^{-1}\sigma ^2-\sigma ^2$$ is then an unbiased estimator of $$\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})$$ for any choice of the selection $$\mathbf {S}^k$$. Under sparsity assumptions [4], we have
$$\begin{aligned} \nu _k = E[\Vert \mathbf {P}_{\mathbf {S}_k}\mathbf {\varepsilon }\Vert ^2_2]\sigma ^{-2} + o[\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})] \mathrm {~as~} n \rightarrow \infty \end{aligned}$$
(5)
with the projection matrix $$\mathbf {P}_{\mathbf {S}^k} = \mathbf {X}_{\mathbf {S}^k} (\mathbf {X}^T_{\mathbf {S}^k}\mathbf {X}_{\mathbf {S}^k})^{-1}\mathbf {X}^T_{\mathbf {S}^k}$$. Given such a projection, the mirror correction $$m_k$$ is found to be
$$\begin{aligned} m_k = \frac{1}{n} E[\Vert \mathbf {P}_{\mathbf {S}^k}\mathbf {\varepsilon }\Vert ^2_2; \mathbf {\beta }]-\frac{k}{n}\sigma ^2, \end{aligned}$$
(6)
meaning that $$m_k = (\nu _k-k)\sigma ^2/n+o[\mathrm {PE}(\widehat{\mathbf {\beta }}_{\mathbf {S}^k})]$$. This expression explicitly writes the parametric dependence on $$\mathbf {\beta }$$. An unbiased estimator is given by
$$\begin{aligned} \widehat{m}_k = \frac{1}{n} E[\Vert \mathbf {P}_{\mathbf {S}^k}\mathbf {\varepsilon }\Vert ^2_2| \mathbf {S}^k; \mathbf {\beta }]-\frac{k}{n}\sigma ^2. \end{aligned}$$
(7)

3 Qualitative Description of the Mirror

Using (7) within the signal-plus-noise model $$\mathbf {Y} = \mathbf {\beta } + \mathbf {\varepsilon }$$, an estimator of the mirror effect $$m_k$$ can be written as
$$\begin{aligned} \widehat{m}_k = \frac{1}{n} E(\Vert \mathbf {\varepsilon }_{\mathbf {S}^k}\Vert ^2_2| \mathbf {S}^k; \mathbf {\beta })-\frac{k}{n}\sigma ^2 \end{aligned}$$
(8)
for any selection $$\mathbf {S}^k$$. The behaviour of this estimator is described in the two following subsections.

3.1 Unstructured Signal-Plus-Noise Models

The mirror effect can be decomposed into three stages depending on the model size k.  
Small selection sizes:

especially if $$k \le n_1$$ (the true number of nonzeros in $$\mathbf {\beta }$$), only nonzero variables should be selected. The errors associated with these variables have an expected variance equal to $$\sigma ^2$$ since they are randomly distributed among these variables. Hence, $$m_k$$ is close to zero.

Intermediate selection sizes:

the large errors are selected accordingly to their absolute value. Their expected variance is obviously greater than $$\sigma ^2$$, meaning that $$m_k$$ is increasing. Its growth is high at first and decreases to zero as smaller errors are added to the selection, leading to the last stage.

Large selection sizes:

finally, only the remaining small errors are selected. This has the effect of diminishing the (previously abnormally high) variance to its original expected value; $$m_k$$ drops to zero which is achieved for the full model.

 
The illustration of the mirror correction is depicted in Fig. 2 (dot-dashed line). The three stages appear approximately in the intervals [0, 1000], [1000, 8000] and [8000, 25000]. Details of the calculations can be found in Sect. 4.
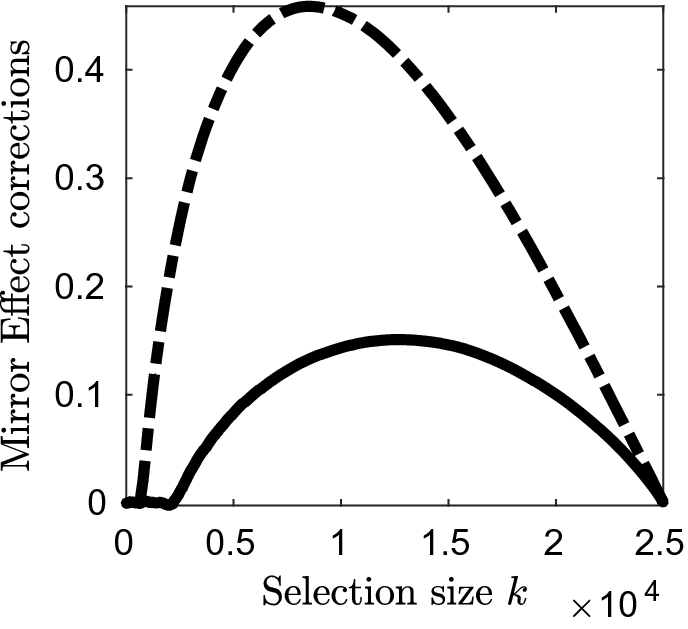
../images/461444_1_En_32_Chapter/461444_1_En_32_Fig2_HTML.png
Fig. 2

Illustration of the mirror correction behaviour for unstructured (dot-dashed line) and group selections (solid) as functions of the model size

3.2 Structured Models: Grouped Variables

We now focus on group selection where l groups are selected and variables that belong to the same group are added to the model altogether. Group-lasso may be the selection procedure used for the construction of the estimator $$\widehat{\mathbf {\beta }}_{\mathbf {S}^l}$$. See Sect. 4 for a more complete definition of $$\widehat{\mathbf {\beta }}_{\mathbf {S}^l}$$.  
Small selection sizes:

groups of nonzero variables are selected first as they have major effects on the linear regression. As before, the associated errors are randomly distributed, so their expected variance equals $$\sigma ^2$$ and $$m_l$$ is roughly zero.

Intermediate selection sizes:

the groups containing only errors are selected accordingly to their norms. These groups typically contain high value errors and some low value errors. Hence, their expected variance is greater than $$\sigma ^2$$ but smaller than in the case of unstructured selection as the latter just selects the largest errors. The consequence on $$m_l$$ is that it increases but its growth, although high at first, is smaller than for the unstructured case.

Large selection size:

groups of small errors are selected (although they can still contain some large errors), meaning that their expected variance decreases to $$\sigma ^2$$ which is achieved for the full model.

 

The explanations above hold for any type of structure, so we can deduce that the unstructured mirror has the largest amplitude in signal-plus-noise models. Indeed, as there is no constraint on the variables, once the nonzeros are selected, the errors are included in the model given their absolute value and more correction is needed in order to temper their effects.

This description is represented in Fig. 2 where the mirror corrections for group and unstructured selections can be visually compared as they are plotted in dot-dashed and solid lines, respectively. The three stages of group selection can be seen in the intervals [0, 2500], [2500, 125000] and [12500, 25000]. Details of the calculations can be found in Sect. 4.

4 Simulation

In this simulation, $$r = 2500$$ groups containing $$w = 10$$ coefficients $$\mathbf {\beta }_j$$ are generated so that $$\mathbf {\beta } = (\mathbf {\beta }_j)_{j = 1,\ldots ,2500}$$ is a n-dimensional vector with $$n = 25000$$. Within group j, the $$\mathbf {\beta }_j$$ coefficients have the same probability $$p_j$$ of being nonzero and, for each group j, a different value $$p_j$$ is randomly drawn from the set $$\mathbf {P} = (0.95,0.80,0.50,0.05,0)$$ with the respective probability $$\mathbf {Q} = (0.02,0.02,0.01,0.20,0.75)$$. The expected proportion of nonzeros is $$\langle \mathbf {P},\mathbf {Q}\rangle = 1/20$$ for the whole vector $$\mathbf {\beta }$$. The nonzeros from $$\mathbf {\beta }$$ are distributed according to the zero inflated Laplace model $$f_{\beta | \beta \ne 0}(\beta ) = (a/2)\exp (-a| \beta |)$$ where $$a = 1/5$$. The observations then are computed as the vector of groups $$(\mathbf {Y}_j)_{j = 1,\ldots ,r} = (\mathbf {\beta }_j)_{j = 1,\ldots ,r} + (\mathbf {\varepsilon }_j)_{j = 1,\ldots ,r}$$, where $$\mathbf {\varepsilon }$$ is an n-vector of independent, standard normal errors.

Estimates $$\widehat{\mathbf {\beta }}$$ are calculated considering two configurations: groups of size $$w = 10$$ (initial setting) and groups of size 1 (unstructured selection). In the latter scenario, $$\widehat{\beta }_i = Y_i S^k_i$$ where $$\mathbf {S}^k$$ is the binary n-vector selecting the k largest absolute values. The 10-group estimator is $$\widehat{\mathbf {\beta }}_j = \mathbf {Y}_j S^l_j$$ where $$\mathbf {S}^l$$ is the binary r-vector selecting the l groups whose $$\ell _2$$ norms are the largest. Using Lasso and group-lasso, respectively, would provide us with the same selections $$\mathbf {S}^k$$ and $$\mathbf {S}^l$$, because of the signal-plus-noise model. Mirror corrections for both configurations are found using (8).

A comparison of the false discovery rates (FDR) of nonzero variables for unstructured and group selections is presented in Fig. 3: because we allow groups to contain zeros and nonzeros in this simulation, at first the recovery rate of the nonzeros in the group setting is below the recovery rate of the unstructured nonzeros. However, the two rates quickly cross and we find the recovery of the nonzeros in the group setting to be better afterwards: particularly, this is the case for the selection that minimises the group-mirror-corrected Cp (marked with the vertical line in Fig. 3).

The FDR of the nonzero groups (groups containing at least one nonzero variable) suggests that the recovery of nonzeros in the group setting will be consistently superior to the recovery of unstructured nonzeros if groups are either fully nonzero or fully zero. In that case, the group-mirror-corrected Cp should perform really well as information criterion to obtain the optimal selection size.
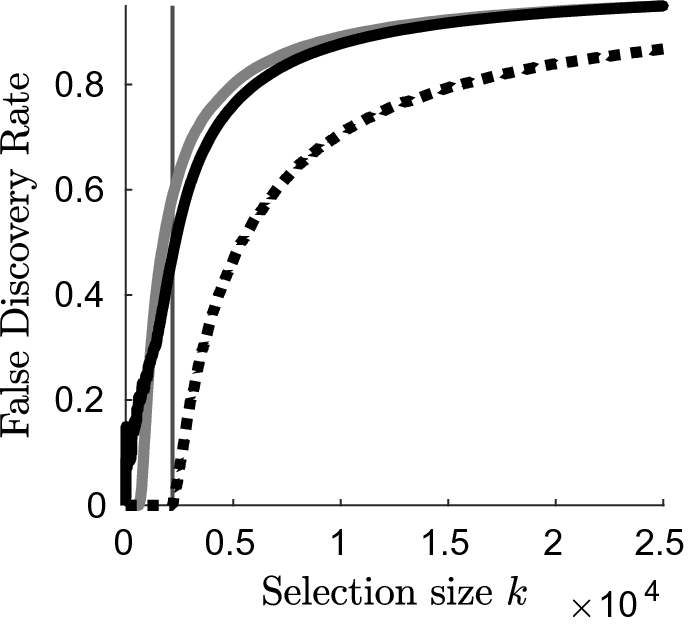
../images/461444_1_En_32_Chapter/461444_1_En_32_Fig3_HTML.png
Fig. 3

Illustration of the false discovery rate (FDR) of nonzero variables for unstructured (grey solid curve) and group selections (black solid curve) as functions of the model size. The vertical line represents the selection size of the best model found with the group-mirror-corrected Cp and the black dotted curve is the FDR of nonzero groups

5 Conclusion

During the optimisation of an information criterion over the model size, using both $$\ell _1$$ and $$\ell _0$$-regularisation for the selection and estimation of variables allows us to take advantage of quadratic programming for the former and least squares projection for the latter. This technique avoids an overestimation of the number of selected variables; however, it requires a corrected expression for the information criterion: the difference between $$\ell _0$$ and $$\ell _1$$ regularisation is compensated using the mirror effect.

In this paper, we described the behaviour of the mirror effect in signal-plus-noise models, observing three stages depending on the model size. This way we can distinguish the selection of nonzero variables, of large false positives and of small false positives for which the mirror is, respectively, close to zero, then increasing and finally decreasing to zero again. In the special case of structured selection, we note a similar behaviour for the mirror although its amplitude is smaller, meaning that the information criterion needs less correction.