© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_35

A Component Multiplicative Error Model for Realized Volatility Measures

Antonio Naimoli1   and Giuseppe Storti1  
(1)
University of Salerno, DISES, Via G. Paolo II, 132, 84084 Fisciano, SA, Italy
 
 
Antonio Naimoli (Corresponding author)
Email: anaimoli@unisa.it
 
Giuseppe Storti
Email: storti@unisa.it

Abstract

We propose a component Multiplicative Error Model (MEM) for modelling and forecasting realized volatility measures. In contrast to conventional MEMs, the proposed specification resorts to the use of a multiplicative component structure in order to parsimoniously parameterize the complex dependence structure of realized volatility measures. The long-run component is defined as a linear combination of MIDAS filters moving at different frequencies, while the short-run component is constrained to follow a unit mean GARCH recursion. This particular specification of the long-run component allows to reproduce very persistent oscillations of the conditional mean of the volatility process, in the spirit of Corsi’s Heterogeneous Autoregressive Model (HAR). The empirical performances of the proposed model are assessed by means of an application to the realized volatility of the S&P 500 index.

Keywords
Realized volatilityComponent Multiplicative Error ModelLong-range dependenceMIDASVolatility forecasting

1 Introduction

In financial econometrics, the last two decades have witnessed an increasing interest in the development of dynamic models incorporating information on realized volatility measures. The reason is that it is believed these models can provide more accurate forecasts of financial volatility than the standard volatility models based on daily squared returns, e.g. the GARCH(1,1).

Engle and Russell  [14] originally proposed the Autoregressive Conditional Duration (ACD) model as a tool for modelling irregularly spaced transaction data observed at high frequency. This model has been later generalized in the class of Multiplicative Error Model (MEM) by [10] for modelling and forecasting positive-valued random variables that are decomposed into the product of their conditional mean and a positive-valued i.i.d. error term with unit mean. Discussions and extensions on the properties of this model class can be found in [4–8, 18, 19], among others.

One of the most prominent fields of application of MEMs is related to the modelling and forecasting of realized volatility measures. It is well known that these variables have very rich serial dependence structures sharing the features of clustering and high persistence. The recurrent feature of long-range dependence is conventionally modelled as an Autoregressive Fractionally Integrated Moving Average (ARFIMA) process as in [3], or using regression models mixing information at different frequencies such as the Heterogeneous AR (HAR) model of [9]. The HAR model, inspired by the heterogeneous market hypothesis of [20], is based on additive cascade of volatility components over different horizons. This particular structure, despite the simplicity of the model, has been found to satisfactorily reproduce the empirical regularities of realized volatility series, including their highly persistent autocorrelation structure.

In this field, component models are an appealing alternative to conventional models since they offer a tractable and parsimonious approach to modelling the persistent dependence structure of realized volatility measures. Models of this type have first been proposed in the GARCH framework and are usually characterized by the mixing of two or more components moving at different frequencies. Starting from the Spline GARCH of [13], where volatility is specified to be the product of a slow-moving component, represented by an exponential spline, and a short-run component which follows a unit mean GARCH process, several contributions have extended and refined this idea. [12] introduced a new class of models called GARCH-MIDAS, where the long-run component is modelled as a MIDAS (Mixed-Data Sampling, [16]) polynomial filter which applies to monthly, quarterly or biannual financial or macroeconomic variables. [2] decomposed the variance into a conditional and an unconditional component such that the latter evolves smoothly over time through a linear combination of logistic transition functions taking time as the transition variable.

Moving to the analysis of intra-daily data, [15] developed the multiplicative component GARCH, decomposing the volatility of high-frequency asset returns into the product of three components, namely, the conditional variance is a product of daily, diurnal and stochastic intra-daily components. Recently [1] have provided a survey on univariate and multivariate GARCH-type models featuring a multiplicative decomposition of the variance into short- and long-run components.

This paper proposes a novel multiplicative dynamic component model which is able to reproduce the main stylized facts arising from the empirical analysis of time series of realized volatility. Compared to other specifications falling into the class of component MEMs, the main innovation of the proposed model can be found in the structure of the long-run component. Namely, as in [21], this is modelled as an additive cascade of MIDAS filters moving at different frequencies. This choice is motivated by the empirical regularities arising from the analysis of realized volatility measures that are typically characterized by two prominent and related features: a slowly moving long-run level and a highly persistent autocorrelation structure. For ease of reference, we will denote the parametric specification adopted for the long-run component as a Heterogeneous MIDAS (H-MIDAS) filter. Residual short-term autocorrelation is then explained by a short-run component that follows a mean reverting unit GARCH-type model. The overall model will be referred to as a H-MIDAS Component MEM model (H-MIDAS-CMEM). It is worth noting that, specifying the long-run component as an additive cascade of volatility filters as in [9], we implicitly associate this component to long-run persistent movements of the realized volatility process.

The model that is here proposed differs from that discussed in [21] under two main respects. First, in this paper, we model realized volatilities on a daily scale rather than high-frequency intra-daily trading volumes. Second, the structure of the MIDAS filters in the long-run component is based on a pure rolling window rather than on a block rolling window scheme.

The estimation of model parameters can be easily performed by maximizing a likelihood function based on the assumption of Generalized F distributed errors. The motivation behind the use of this distribution is twofold. First, nesting different distributions, the Generalized F results very flexible in modelling the distributional properties of the observed variable. Second, it can be easily extended to control the presence of zero outcomes [17].

In order to assess the relative merits of the proposed approach we present the results of an application to the realized volatility time series of the S&P 500 index in which the predictive performance of the proposed model is compared to that of the standard MEM by means of an out-of-sample rolling window forecasting experiment. The volatility forecasting performance has been assessed using three different loss functions, the Mean Squared Error (MSE), the Mean Absolute Error (MAE) and the QLIKE. The Diebold-Mariano test is then used to evaluate the significance of differences in the predictive performances of the models under analysis. Our findings suggest that the H-MIDAS-CMEM significantly outperforms the benchmark in terms of forecasting accuracy.

The remainder of the paper is structured as follows. In Sect. 2, we present the proposed H-MIDAS-CMEM model, while the estimation procedure is described in Sect. 3. The results of the empirical application are presented and discussed in Sect. 4. Finally, Sect. 5 concludes.

2 Model Specification

Let $$\{ v_{t,i} \}$$ be a time series of daily realized volatility (RV) measures observed on day i in period t, such as in a month or a quarter. The general H-MIDAS-CMEM model can be formulated as
$$\begin{aligned} v_{t,i}= \tau _{t,i} \, g_{t,i} \,\, \varepsilon _{t,i}, \qquad \varepsilon _{t,i}|\mathscr {F}_{t,i-1} \overset{iid}{\sim } \mathscr {D}^+(1,\sigma ^2) \, , \end{aligned}$$
(1)
where $$\mathscr {F}_{t,i-1}$$ is the sigma-field generated by the available intra-daily information until day $$(i-1)$$ of period t. The conditional expectation of $$v_{t,i}$$, given $$\mathscr {F}_{t,i-1}$$, is the product of two components characterized by different dynamic specifications. In particular, $$g_{t,i}$$ represents a daily dynamic component that reproduces autocorrelated movements around the current long-run level, while $$\tau _{t,i}$$ is a smoothly varying component given by the sum of MIDAS filters moving at different frequencies. This component is designed to track the dynamics of the long-run level of realized volatility.1 In order to make the model identifiable, as in [12], the short-run component is constrained to follow a mean reverting unit GARCH-type process. Namely, $$g_{t,i}$$ is specified as
$$\begin{aligned} g_{t,i} = \omega ^* + \sum _{j=1}^{r}\alpha _j \frac{v_{t,i-j}}{\tau _{t,i-j}} + \sum _{k=1}^{s}\beta _k \, g_{t,i-k}, \qquad \tau _{t,i}>0 \quad \forall _{t,i} \,\, . \end{aligned}$$
(2)
To fulfill the unit mean assumption on $$g_{t,i}$$, it is necessary to set appropriate constraints on $$\omega ^*$$ by means of a targeting procedure. In particular, taking the expectation of both sides of $$g_{t,i}$$, it is easy to show that
$$ \omega ^*=(1-\sum _{j=1}^{r}\alpha _j-\sum _{k=1}^{s}\beta _k). $$
Positivity of $$g_{t,i}$$ is then ensured by setting the following standard constraints: $$\omega ^*>0$$, $$\alpha _j\ge 0$$ for $$j=1,\ldots ,r$$, and $$\beta _k\ge 0$$ for $$k=1,\ldots ,s$$.2
On the other hand, the low-frequency component is modelled as a linear combination of MIDAS filters of past volatilities aggregated at different frequencies. A general formulation of the long-run component is given by
$$\begin{aligned} \begin{aligned} log (\tau _{t,i}) = \delta&+ \theta _s \sum _{k=1}^{K}\varphi _k(\omega _{1,s}, \, \omega _{2,s}) \, log \left( VS^{(k)}_{t,i} \right) \\&+ \theta _m \sum _{h=1}^{K^*} \varphi _{h}(\omega _{1,m}, \, \omega _{2,m})\, log \left( VM^{(h)}_{t,i} \right) , \end{aligned} \end{aligned}$$
(3)
where $$VS^{(k)}_{t,i}$$ and $$VM^{(h)}_{t,i}$$ denote the RV aggregated over a rolling window of length equal to $$n_s$$ and $$n_m$$, respectively, with $$n_s > n_m$$, while K is the number of MIDAS lags and $$K^* = K+n_s-n_m$$. In particular,
$$\begin{aligned} VS^{(k)}_{t,i} = \sum _{j=1}^{n_s} v_{t,i-(k-1)-j} \qquad \text{ for } k=1,\ldots , K \end{aligned}$$
(4)
and
$$\begin{aligned} VM^{(h)}_{t,i} = \sum _{j=1}^{n_m} v_{t,i-(h-1)-j} \qquad \text{ for } h=1,\ldots , K^* \, . \end{aligned}$$
(5)
In the empirical application, we choose $$n_s=125$$ implying a biannual rolling window RV and $$n_m=22$$, meaning that the RV is rolled back monthly. Furthermore, the long-run component is considered in terms of logarithmic specification since it does not require parameter constraints to ensure the positivity of $$\tau _{t,i}$$.
Finally, the weighting function $$\varphi (\underline{\omega })$$ is computed according to the Beta weighting scheme which is generally defined as
$$\begin{aligned} \varphi _k(\omega _1, \omega _2)=\frac{(k/K)^{\omega _{1}-1}(1-k/K)^{\omega _{2}-1}}{\sum _{j=1}^{K}(j/K)^{\omega _{1}-1}(1-j/K)^{\omega _{2}-1}}, \end{aligned}$$
(6)
where the weights in Eq. (6) sum up to 1. As discussed in [16], this Beta-specification is very flexible, being able to accommodate increasing, decreasing or hump-shaped weighting schemes, where the number of lags K need to be properly chosen by information criteria to avoid overfitting problems.

This multiple frequency specification appears to be preferable to the single-frequency MIDAS filter for at least two different reasons. First, the modeller is not constrained to choose a specific frequency for trend estimation, but can determine the optimal blend of low- and high-frequency information in a fully data-driven fashion. Second, as pointed out in [9], an additive cascade of linear filters, applied to the same variable aggregated over different time intervals, can allow to reproduce very persistent dynamics such as those typically observed for realized volatilities. We have also investigated the profitability of adding more components to the specification of $$\tau _{t,i}$$. However, this did not lead to any noticeable improvement in terms of fit and forecasting accuracy.

3 Estimation

The model parameters can be estimated in one step by Maximum Likelihood (ML), assuming that the innovation term follows a Generalized F (GF) distribution. Alternatively, estimation could be performed by maximizing a quasi-likelihood function based on the assumption that the errors $$\varepsilon _{t,i}$$ are conditionally distributed as a unit Exponential distribution that can be seen as the counterpart of the standard normal distribution for positive-valued random variables [10, 11]. To save space, here we focus on ML estimation based on the assumption of GF errors.

In particular, let X be a non-negative random variable, the density function of a GF random variable is given by
$$\begin{aligned} f(x;\underline{\zeta })=\frac{ax^{ab-1}[c+(x/\eta )^a]^{(-c-b)}\,c^c}{\eta ^{ab}\,\mathscr {B}(b,c)}, \end{aligned}$$
(7)
where $$\underline{\zeta }=(a,b,c,\eta )^\prime $$, $$a>0$$, $$b>0$$, $$c>0$$ and $$\eta >0$$, with $$\mathscr {B}(\cdot ,\cdot )$$ the Beta function such that $$\mathscr {B}(b,c)=[ \Gamma (b)\Gamma (c) ] / \Gamma (b+c)$$. The GF distribution is based on a scale parameter $$\eta $$ and three shape parameters a, b and c, and thus it is very flexible, nesting different error distributions, such as the Weibull for $$b=1$$ and $$c\rightarrow \infty $$, the generalized Gamma for $$c\rightarrow \infty $$ and the log-logistic for $$b=1$$ and $$c=1$$. The Exponential distribution is also asymptotically nested in the GF for $$a=b=1$$ and $$c\rightarrow \infty $$.

Note that in the presence of zero outcomes the Zero-Augmented Generalized F (ZAF) distribution [17] can be used.

In order to ensure that the unit mean assumption for $$\varepsilon _{t,i}$$ is fulfilled, we need to set $$\eta =\xi ^{-1}$$, where
$$\begin{aligned} \xi =c^{1/a}\left[ \Gamma (b+1/a)\Gamma (c-1/a)\right] \left[ \Gamma (b)\Gamma (c)\right] ^{-1}. \end{aligned}$$
The log-likelihood function is then given by
$$\begin{aligned} \begin{aligned} \mathscr {L}(\underline{v};\underline{\vartheta }) =&\sum _{t,i} \left\{ log \, a + (ab-1) \, log \left( \varepsilon _{t,i} \right) + c \, log \, c -(c+b) \, log \left[ c + \left( \xi \varepsilon _{t,i}\right) ^a \right] + \right. \\&\left. -log ( \tau _{t,i} \, g_{t,i} ) - log \, \mathscr {B}(b,c) + ab\,log( \xi ) \right\} , \end{aligned} \end{aligned}$$
(8)
where $$\varepsilon _{t,i}=\frac{v_{t,i}}{\tau _{t,i} \, g_{t,i}}$$ and $$\underline{\vartheta }$$ is the parameter vector to be estimated.

4 Empirical Application

To assess the performance of the proposed model, in this section, we present and discuss the results of an empirical application to the S&P 500 realized volatility series.3 The 5-min intra-daily returns have been used to compute the daily RV series covering the period between 03 January 2000 and 27 December 2018 for a total of 4766 observations. The analysis has been performed using the software R [23].

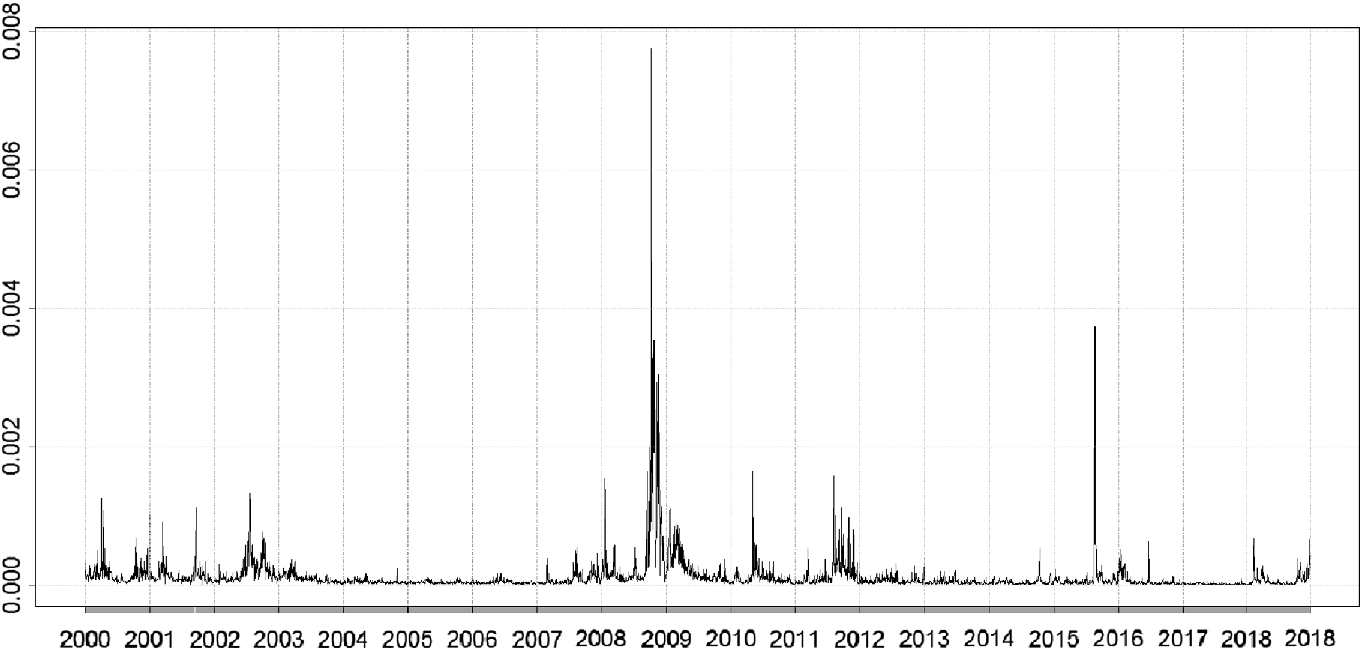
Graphical inspection of the S&P 500 realized volatility, displayed in Fig. 1, reveals several periods of high volatility. These essentially refer to the dot com bubble in 2002, the financial crisis starting in mid-2007 and peaking in 2008 and the crisis in Europe progressed from the banking system to a sovereign debt crisis with the highest turmoil level in the late 2011. More recently, the stock market sell-off that occurred between June 2015 and June 2016 is related to different events such as the Chinese stock market turbulence, but also to the uncertainty around FED interest rates, oil prices, Brexit and the U.S. presidential election. Finally, economic and political uncertainties are the most prevalent drivers of market volatility in 2018.
../images/461444_1_En_35_Chapter/461444_1_En_35_Fig1_HTML.png
Fig. 1

S&P 500 Realized Volatility

The model parameters have been estimated by ML, relying on the assumption of GF errors and, as a robustness check, by Exponential QML. Estimation results, based on the full sample 5-min RV, are reported in Tables 1 and 2, respectively. For ML, standard errors are based on the numerically estimated Hessian at the optimum, whereas for QML, we resort to the usual sandwich estimator. The performance of the H-MIDAS-CMEM has been compared to that of the standard MEM(1,1) specification, considered as benchmark model.
Table 1

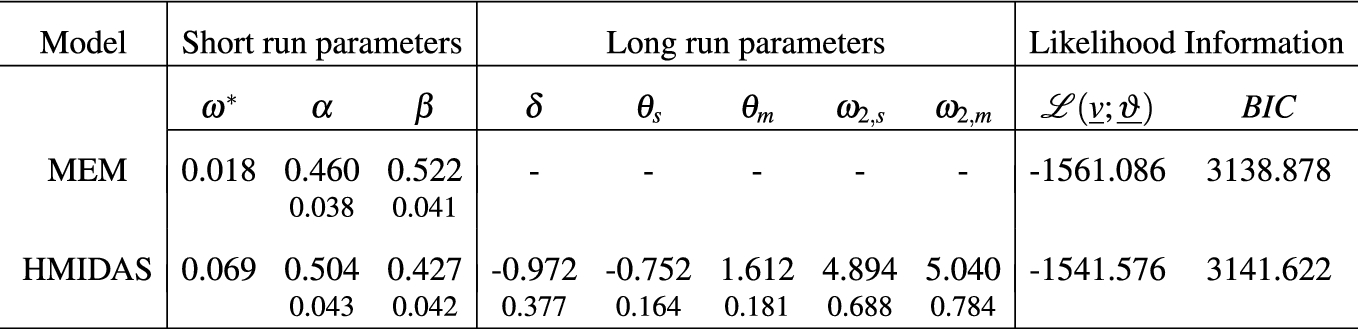
In sample parameter estimates for the Generalized F distribution

../images/461444_1_En_35_Chapter/461444_1_En_35_Figa_HTML.png
 

Parameter estimates for MEM and H-MIDAS-CMEM. Estimation is performed on the full sample period 03 Jan 2000–27 Dec 2018 using the GF distribution. Standard errors are reported in smaller font under the parameter values. All parameters are significant at 5%

Regarding the H-MIDAS-CMEM, the short-run component follows a mean reverting unit GARCH(1,1) process, while the long-term component is specified as a combination of two MIDAS filters moving at a semiannual ($$n_s=125$$) and a monthly ($$n_m=22$$) frequency, with K corresponding to two MIDAS lag years. It is worth noting that, although the Beta lag structure in (6) includes two parameters, following a common practice in the literature on MIDAS models, in our empirical applications, $$\omega _{1,s}$$ and $$\omega _{1,m}$$ have been set equal to 1 in order to have monotonically decreasing weights over the lags.

The panel of the short-term component in Table 1 shows that the intercept $$\omega ^*$$ is slightly higher for the H-MIDAS-CMEM than the standard MEM. Furthermore, standard errors for $$\omega ^*$$ are missing since it is estimated through the expectation targeting procedure. The parameter $$\alpha $$ takes values much larger than those typically obtained fitting GARCH models to log-returns, while the opposite holds for $$\beta $$. The analysis of the long-run component reveals that all the involved parameters in $$log(\tau _{t,i})$$ are statistically significant. In particular, the slope coefficient $$\theta _s$$ of the biannual filter is negative, while $$\theta _m$$ associated to the monthly filter is positive. Moreover, the coefficients $$\omega _{2,s}$$ and $$\omega _{2,m}$$ defining the features of the Beta weighting function take on values such that the weights slowly decline to zero over the lags. Finally, the panel referring to the error distribution parameters indicates that the GF coefficients are similar between MEM and H-MIDAS-CMEM.

From a comparison of the log-likelihoods, it clearly emerges that the value recorded for the H-MIDAS-CMEM is much larger than that of the competing model. In addition, the BIC reveals that there is a big improvement coming from the inclusion of the heterogeneous component in the MIDAS trend which allows to better capture the changes in the dynamics of the average volatility level.

In the QML case (Table 2), the estimated short-run component parameters are reasonably close to those reported for ML estimation. This is, however, not true for the parameters of the long-run component. As expected, the BIC values are always larger than the ones obtained under the GF distribution.
Table 2

In sample parameter estimates for the Exponential distribution

../images/461444_1_En_35_Chapter/461444_1_En_35_Figb_HTML.png
 

Parameter estimates for MEM and H-MIDAS-CMEM. Estimation is performed on the full sample period 03 Jan 2000–27 Dec 2018 using the Exponential distribution. Robust standard errors are reported in smaller font under the parameters value. All parameters are significant at 5%

The out-of-sample predictive ability of the models, for the S&P 500 RV time series, has been assessed via a rolling window forecasting exercise leaving the last 500 observations as out-of-sample forecasting period, that is, 30 December 2016–27 December 2018.

The predictive performance of the examined models is evaluated by computing the Mean Squared Error (MSE), Mean Absolute Error (MAE) and QLIKE [22] loss functions, using the 5-min RV as volatility proxy, namely,
$$\begin{aligned} MSE&= \sum _{t=1}^{T}\sum _{i=1}^{I}(v_{t,i} - \hat{v}_{t,i})^2; \\ MAE&= \sum _{t=1}^{T}\sum _{i=1}^{I}|v_{t,i} - \hat{v}_{t,i}|; \\ QLIKE&= \sum _{t=1}^{T}\sum _{i=1}^{I} log(\hat{v}_{t,i}) + \frac{v_{t,i}}{\hat{v}_{t,i}}. \end{aligned}$$
The significance of differences in forecasting accuracy is assessed by means of the two-sided Diebold-Mariano test under the null hypothesis that MEM and H-MIDAS-CMEM exhibit the same forecasting ability.
Table 3

S&P 500 out-of-sample loss functions comparison

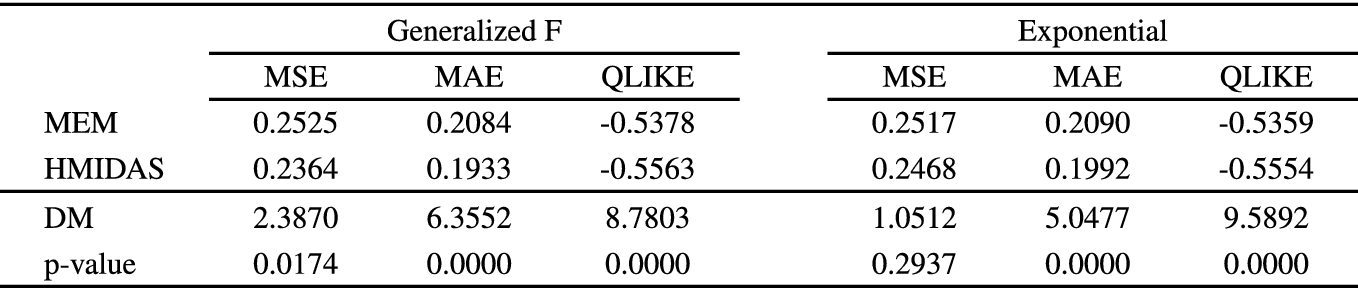../images/461444_1_En_35_Chapter/461444_1_En_35_Figc_HTML.png
 

Top panel: loss function average values for Mean Squared Error (MSE), Mean Absolute Error (MAE) and QLIKE. Bottom panel: Diebold-Mariano test statistics (DM) with the corresponding p-values. Positive statistics are in favour of the H-MIDAS-CMEM model. Values in the table refer to models fitted using the Generalized F distribution (left panel) and the Exponential distribution (right panel). Better models correspond to lower losses

The out-of-sample performance of the fitted models is summarized in Table 3, reporting the average values of the considered loss functions (top panel) and the Diebold-Mariano (DM) test statistics, together with the associated p-values (bottom panel). The empirical results suggest that the H-MIDAS-CMEM always returns average losses that are significantly lower than those recorded for the benchmark MEM. The only exception occurs for the MSE when models are fitted by Exponential QML. In this case, the H-MIDAS-CMEM still returns a lower average loss, but the null of equal predictive ability cannot be rejected. Finally, comparing forecasts based on models fitted by MLE and QMLE, respectively, we find that there are no striking differences between these two sets of forecasts, with the former returning slightly lower average losses.

5 Concluding Remarks

This paper investigates the usefulness of the application of the Heterogeneous MIDAS Component MEM (H-MIDAS-CMEM) for fitting and forecasting realized volatility measures. The introduction of the heterogeneous MIDAS component, specified as an additive cascade of linear filters which take on different frequencies, allows to better capture the main empirical properties of the realized volatility, such as clustering and memory persistence. The empirical analysis of the realized volatility series of the S&P 500 index points out that the H-MIDAS-CMEM outperforms the standard MEM model in fitting the S&P 500 volatility. At the same time, the out-of-sample comparison shows that, for all the loss functions considered, the H-MIDAS-CMEM significantly outperforms the benchmark in terms of predictive accuracy. These findings appear to be robust to the choice of the error distribution. Accordingly, gains in predictive ability are mainly determined by the dynamic structure of the H-MIDAS-CMEM, rather than from the estimation method (MLE versus QMLE).

Finally, although the model discussed in this paper is motivated by the empirical properties of realized volatility measures, our approach can be easily extended to the analysis of other financial variables sharing the same features, such as trading volumes, bid-ask spreads and durations.