© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_45

Monte Carlo Permutation Tests for Assessing Spatial Dependence at Different Scales

Craig Wang1   and Reinhard Furrer1, 2  
(1)
Department of Mathematics, University of Zurich, Zurich, Switzerland
(2)
Department of Computational Science, University of Zurich, Zurich, Switzerland
 
 
Craig Wang (Corresponding author)
Email: craig.wang@math.uzh.ch
 
Reinhard Furrer
Email: reinhard.furrer@math.uzh.ch

Abstract

Spatially dependent residuals arise as a result of missing or misspecified spatial variables in a model. Such dependence is observed in different areas, including environmental, epidemiological, social and economic studies. It is crucial to take the dependence into modelling consideration to avoid spurious associations between variables of interest or to avoid wrong inferential conclusions due to underestimated uncertainties. An insight about the scales at which spatial dependence exist can help to comprehend the underlying physical process and to select suitable spatial interpolation methods. In this paper, we propose two Monte Carlo permutation tests to (1) assess the existence of overall spatial dependence and (2) assess spatial dependence at small scales, respectively. A p-value combination method is used to improve statistical power of the tests. We conduct a simulation study to reveal the advantages of our proposed methods in terms of type I error rate and statistical power. The tests are implemented in an open-source R package variosig.

Keywords
Spatial dataCombining p-valuesEmpirical Brown’s methodVariogramNonparametric

1 Introduction

Independent and identically distributed residuals are a key assumption in many statistical analysis models. When analyzing spatial, i.e. geolocated data, this assumption is violated if one fails to account for the existence of spatial dependence in the modelling components. Such violation can lead to biased parameter estimates and spurious associations between the dependent variable and its covariates. Therefore, it is important to take spatial dependence into modelling consideration when it exists. Spatially dependent data arise in many research domains, for example in spatial epidemiology where researchers are interested in the relationship between disease prevalence and risk factors [9, 23], in economics where it is of interest to identify regions of housing externalities [15] or in ecological studies where species distribution needs to be mapped [10, 17]. The scales of spatial dependence also play an important role in understanding the underlying physical and biological processes [10, 17].

The assessment of spatial dependence and its scales is often done by plotting and modelling the empirical semi-variogram estimates, based on extracted residuals after first-stage statistical modelling. If the empirical semi-variogram indicates spatial dependence, then the model needs to be adjusted to account for the remaining dependence. However, semi-variogram estimates can be sensitive to outliers, choice of distance binning and sampling design. Several robust variogram estimators [4, 7] and methods to quantify uncertainty of variogram estimates [3, 5, 12] are available. One can use a maximum likelihood estimator and its uncertainty estimate to assess the spatial dependence, or use parametric bootstrap [16] by firstly fitting a variogram model and simulate new values based on the estimated model to obtain additional variogram estimates hence an uncertainty estimate. However, both approaches require a pre-defined variogram model and a sufficient sample size. An alternative approach to assess the existence of spatial dependence is to use a Monte Carlo permutation test. The permutation test is a nonparametric approach that does not make any assumptions on the distribution of residuals. Walker et al. [21] introduced a permutation test to permute the residual values across spatial locations, in order to simulate under the null hypothesis of complete spatial randomness. Diblasi and Bowman [5] compared the performance of a permutation test on their proposed test statistics based on the assumption of normally distributed residuals. Viladomat et al. [20] used a permutation method in a two-step procedure to test the correlation of two variables when they both exhibit spatial dependence.

In this paper, we propose two Monte Carlo permutation tests to assess the existence of overall spatial dependence and spatial dependence specifically at small scales, respectively. We demonstrate that our proposed methods have more accurate type I error rate compared to the standard permutation test in [21] and achieve good statistical power at the same time.

2 Assessing Spatial Dependence at Different Scales

We assume that trend components have been taken out of data, so we work with residuals. Let $${Y(s):s \in D \subseteq R^2}$$ be a zero-mean second-order stationary spatial process that is observed at coordinates s, then the semi-variogram is defined as
$$\begin{aligned} \gamma (h) = \frac{1}{2}\text {Var}\left( Y(s+h) - Y(s)\right) , \end{aligned}$$
(1)
where h is the spatial lag, with an estimator as the empirical semi-variogram
$$\begin{aligned} \hat{\gamma }(h) = \frac{1}{2\vert N(h)\vert }\sum _{N(h)}(Y(s_i) - Y(s_j))^2, \end{aligned}$$
(2)
where N(h) denotes the set of all pairs whose spatial locations are separated by distance between $$[h - \delta ,h + \delta ]$$. In practice, different distance binnings $$h_1,\dots ,h_k$$ are used to obtain empirical semi-variogram estimates $$\hat{\gamma }(h_d)$$ for $$d=1,\dots ,k.$$

2.1 Permutation Test for Overall Spatial Dependence

The permutation test for overall spatial dependence has been described in [21]. Under the null hypothesis of complete spatial randomness, residuals are permuted randomly over all locations. With such permutation, the spatial dependence at any scale is destroyed. There are n! number of possible permutations for n locations, hence the Monte Carlo method with a fixed number of permutations is often used to save computation time. Pointwise p-values based on semi-variogram estimates can be computed as
$$\begin{aligned} p_d = \frac{1}{n_{mc}}\sum _{i=1}^{n_{mc}} I_{\{\hat{\gamma }_i(h_d) \le \hat{\gamma }(h_d)\}} \end{aligned}$$
(3)
for the dth distance binning, where $$n_{mc}$$ is the number of Monte Carlo iterations and $$\hat{\gamma }_i(h_d)$$ is the dth semi-variogram estimates from the ith permuted samples. Walker et al. [21] compared the p-values in Eq. (3) with a type I error rate $$\alpha $$, and deemed that the null hypothesis is rejected if any p-value is below $$\alpha $$. This approach implicitly used the p-value combination method proposed in [19], which takes the overall p-value $$\varPsi _T = \min (p_d)$$ and compares it with $$\alpha $$. When the evidence of spatial dependence is relatively strong, the p-values tend to be small. In such cases, the null hypothesis will be rejected as long as one of the p-values is smaller than $$\alpha $$. However, when none of the p-values are smaller than $$\alpha $$ under settings of weak spatial dependence, the rejection region of using overall p-value $$\varPsi _T$$ is smaller than using other p-value combination methods (e.g. [6, 11]). This will lead to smaller statistical power. In addition, using the minimum p-value can inflate the type I error which leads to spurious spatial dependence. To mitigate these problems, we propose a modified permutation test for overall spatial dependence.

2.2 Modified Permutation Test for Overall Spatial Dependence

We describe a modified version of the permutation test, which still uses p-values obtained via Monte Carlo permutations but combines them more appropriately. Under the null hypothesis of no spatial dependence, p-values are uniformly distributed. Fisher’s method [6] was proposed to combine p-values based on independent test statistics into a single $$\chi ^2$$-distributed test statistic. If we assume the test statistics $$\gamma (h_d)$$ are mutually independent, then the Fisher’s method states
$$\begin{aligned} \varPsi _F = -2 \sum _{d=1}^{k} \log (P_d) \sim \chi ^2_{2k}. \end{aligned}$$
(4)
However, the semi-variogram estimates are not mutually independent since each estimate is based on an overlapping set of residual values from the same data. Failing to account for positive correlation between test statistics tends to give under-estimated combined p-value. Conversely, failing to account for negatively correlated test statistics gives an over-estimated combined p-value.
We propose a modified version of the permutation test for overall spatial dependence using the empirical Brown’s method [13], an extension of the Fisher’s method, for combining dependent p-values from multivariate normal test statistics. Under the null hypothesis of no spatial dependence, we assume that the residual value at each location is normally distributed as $$Y(s) \sim N(0, \sigma ^2)$$. For locations $$s_1,\dots ,s_n$$, let $$\mathbf {Y} = (Y(s_1),\dots ,Y(s_n))^\top $$. The dth semi-variogram then follows a scaled $$\chi ^2$$-distribution with $$r_d$$ degrees of freedom, i.e.
$$\begin{aligned} \gamma (h_d) = \frac{1}{N(h)}\mathbf {Y}^\top \mathbf {A}_d \mathbf {Y} \sim \chi ^2_{r_d}/N(h), \end{aligned}$$
(5)
if the matrix $$\mathbf {A}_d$$ is idempotent and has rank $$r_d$$ [1]. The matrix $$\mathbf {A}_d$$ is the spatial design matrix of the data at lag d [7]. For non-gridded locations, the matrix is close to idempotent if the number of semi-variogram estimate is not too small, which yields Eq. (5) as a good approximation. For moderate to large ranks, $$\chi ^2_{r_d}/N(h) \xrightarrow {d} N(r_d/N(h),2r_d/N(h)^2)$$. Therefore, we can approximate the vector of test statistics $$[\gamma (h_1), \gamma (h_2), \dots , \gamma (h_k)]^\top $$ with a multivariate normal distribution. The Brown’s method [2] allows us to derive a scaled $$\chi ^2$$-distribution to replace $$\chi ^2_{2k}$$ from the Fisher’s method. The overall test statistic stays as $$\varPsi _F$$; however, the distribution under the null hypothesis becomes a scaled chi-squared distribution $$c\chi ^2_{2f}$$, with
$$\begin{aligned} \displaystyle f&= \frac{2k^2}{2k + s},\qquad c = 1 + \frac{s}{2k}, \text {~~where}\nonumber \\ s&= \sum _{i<j} \text {cov}(-2\log P_i, -2\log P_j). \end{aligned}$$
(6)
The evaluation of the covariance terms in Eq. (6) requires numerical integration, and can be approximated using either a polynomial regression based on the correlation between test statistics [8] or the empirical Brown’s method to obtain approximated samples of $$P_i$$ and $$P_j$$ [13]. The latter has been shown to be more robust compared to polynomial approximation when there is deviation from normality in the test statistics. In our modified permutation test, we use the empirical Brown’s method to combine the p-values generated by Monte Carlo permutations into an overall test statistic and compare it with $$c\chi ^2_{2f}$$.

2.3 Permutation Test for Spatial Dependence at Small Scales

Sometimes the existence of scale-specific spatial dependence is a more meaningful hypothesis to test against. We propose a permutation test to permute the residuals in a way such that only small-scale dependence is destroyed.

Instead of randomly permuting the residuals over all spatial locations, we first apply a clustering algorithm on the locations to divide them into small clusters. The clustering algorithm should not result in clusters that have a high variance in size. Popular algorithms such as k-means or hierarchical clustering can be used, or simply hex-binning when the locations are evenly distributed over the spatial domain. After clusters are defined, the residuals are randomly permuted only within each cluster. The null hypothesis then concerns only the first few semi-variogram estimates at small scale. The clustering algorithm should be tuned depending on the scale of interest. Since there are still correlations among the pointwise p-values, we use the empirical Brown’s method to combine them to get an overall test statistic.

Figure 1 shows semi-variogram estimates based on a simulated set of residuals in 200 locations in a unit square and an exponential covariance function $$\gamma (h) = 0.5\exp (-0.05h) + 0.5$$. In this case, spatial dependence only exists at small scales. The 95% confidence band shown in light blue is based on random permutation where all of the spatial dependence is destroyed. The 95% confidence band in red is based on cluster permutation where only the small-scale spatial dependence is destroyed. The latter allows more powerful hypothesis testing focusing only on a small scale, as we will show in the simulation results.
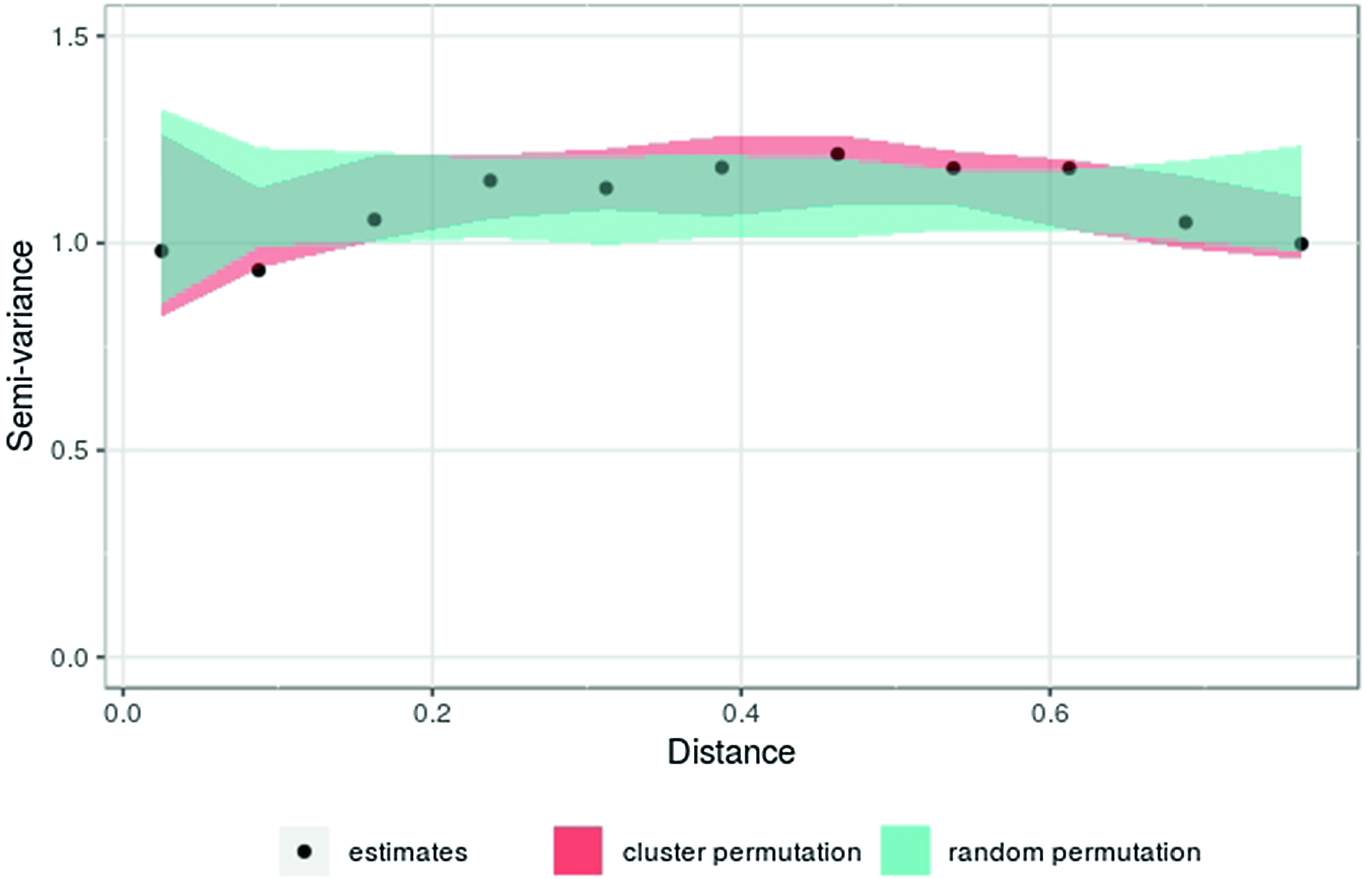
../images/461444_1_En_45_Chapter/461444_1_En_45_Fig1_HTML.png
Fig. 1

Semi-variogram estimates based on simulated residuals. Ribbons indicate 95% confidence band of permutation samples. The original and modified permutation test for overall spatial dependence provided p-values of 0.001 and 0.078, respectively, while the cluster permutation method provided an overall p-value of 0.027

3 Simulation Study

We conduct a simulation study to compare the permutation tests in terms of type I error rate and statistical power of detecting spatial dependence. The null hypothesis of random permutation is that there is no spatial dependence, while the null hypothesis of cluster permutation is that there is no spatial dependence at small scales.

3.1 Simulation Setup

We simulate a Gaussian process on n uniformly distributed locations within a $$[0,1]\times [0,1]$$ domain. Without loss of generality, we assume the Gaussian process has an exponential covariance function from the Matérn family, i.e. $$\text {Cov}(Y(s_i), Y(s_j)) = \sigma ^2\exp (||s_i - s_j||/\phi ) + \tau ^2$$, where $$||s_i - s_j||$$ denotes the Euclidean distance between locations $$s_i$$ and $$s_j$$. The magnitude of spatial covariance is represented by $$\sigma ^2$$, the magnitude of noise is $$\tau ^2$$. The spatial range $$\phi $$ controls the covariance decay over distance, which corresponds to an effective range of $$3\phi $$ for the exponential covariance function. Hence, 95% of the spatial correlation disappears at distance $$3\phi $$.

We simulate a total of 10 different spatial dependence structures each with 5 different sample sizes, where $$n = \{50,100,200,300,500\}$$, $$\phi = \{0.05, 0.2\}$$ and $$\sigma ^2/\tau ^2 = \{0/0.5,0.25/1,0.5/1,0.5/0.5,1/0.5\}$$. Different $$\sigma ^2/\tau ^2$$ represents differing strengths of spatial dependence. We choose $$n_{mc} = 1000$$ and repeat each scenario 1000 times. For the cluster permutation, we use k-means clustering with 5 clusters when $$n = 50$$, and with 10 clusters for all other sample sizes. The null hypothesis is that the first two semi-variogram estimates are 0, which corresponds to no spatial dependence at a distance smaller than approximately 0.1. All the simulation results are obtained in R version 3.5 [14].

3.2 Simulation Results

Figure 2 shows the simulation results. The permutation test for overall spatial dependence (denoted as random+min) using minimum p-value is shown in solid lines; the modified permutation test for overall spatial dependence with empirical Brown’s method (denoted as random+ebm) is shown in dotted lines; the permutation test for spatial dependence at small scales with empirical Brown’s method (denoted as cluster+ebm) is shown in dashed lines.

The first permutation test has the highest power, since it uses the minimum p-value across semi-variogram estimates without any adjustment. This makes the null hypothesis easy to reject. As a result of this, the type I error rate is inflated to around 37% at a nominal level of 5%. After combining the individual p-values using empirical Brown’s method, our proposed modified permutation test obtained close-to-nominal type I error rate. This comes at a cost of losing some statistical power. When the main interest is to test the existence of spatial dependence at small scale, the clustering-based permutation test boosts the statistical power compared to the modified permutation test while maintaining the correct type I error rate. It can be observed from the first row, where spatial dependence exists at small scales with $$\phi = 0.05$$, the power of the clustering-based permutation test is higher than the modified permutation test.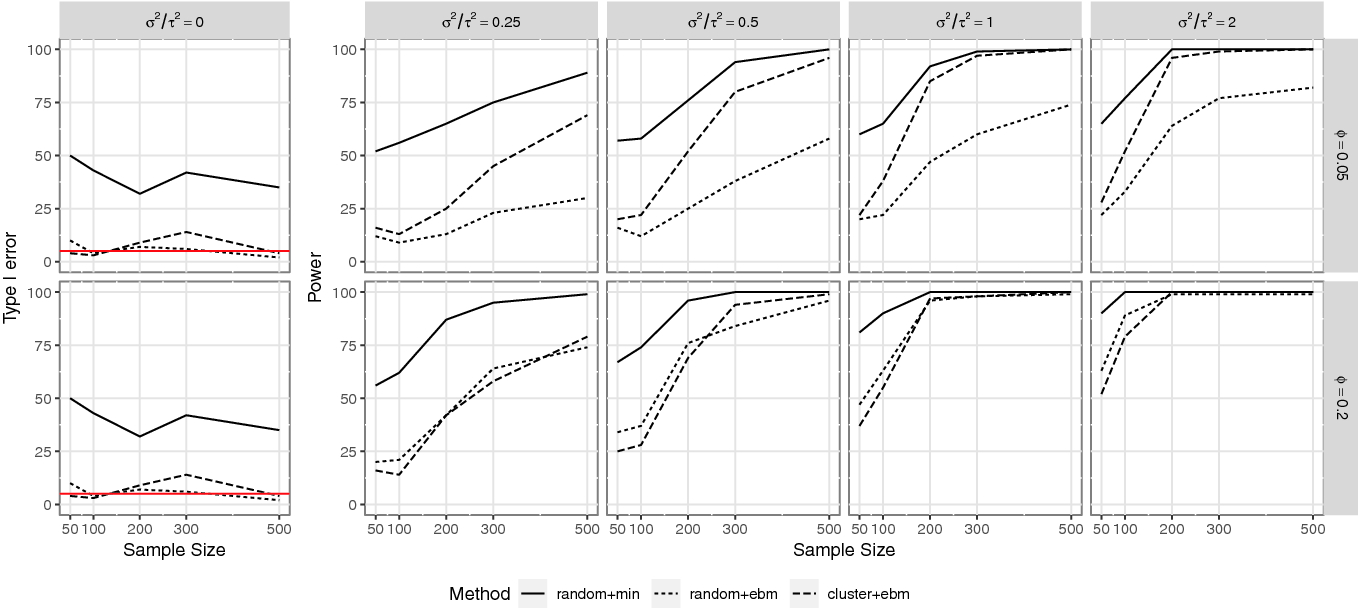
../images/461444_1_En_45_Chapter/461444_1_En_45_Fig2_HTML.png
Fig. 2

Simulation results showing type I error rate (first column) and statistical power (other columns) of three different permutation tests for different scenarios. The horizontal red line in the first column shows the nominal type I error rate at 5%

4 Discussion and Outlook

This paper presents two new approaches of testing spatial dependence using Monte Carlo permutation tests. The first is a modified version of the permutation test for overall spatial dependence. Instead of using the minimum p-values at different distance binnings as the overall p-value, we propose a modified version that uses empirical Brown’s method to combine the p-values into a new test statistic. The second is a clustering-based permutation test for spatial dependence at small scales. Instead of the null hypothesis of complete spatial randomness, sometimes it is of interest to focus only on the existence of spatial dependence at small scales. In such a situation, our proposed approach can improve the statistical power compared to using an overall permutation test. Both approaches are implemented in the open-source software package variosig [20] available on the Comprehensive R Archive Network (CRAN, https://​cloud.​r-project.​org/​).

Our simulation study shows that the type I error rate is maintained by the modified permutation test for overall spatial dependence and the clustering-based permutation test for spatial dependence at small scales. The clustering-based permutation test has increased statistical power compared to the modified permutation test when the sample size is not too small. When the interest is spatial dependence at small scales, the clustering-based permutation test should be used.

In addition to permutation tests, our proposed clustering-based permutation method can also be used in conjunction with a functional boxplot [18] to obtain a visual inspection of the spatial dependence at small scales. The permutation tests can also be applied to large spatial datasets, since it is computationally efficient and can be tuned using the number of permutations. Finally, the result of our permutation tests can help to inform about subsequent analysis such as spatial interpolation, scale decomposition and regression modelling.

Acknowledgements

This work was supported by the Swiss National Science Foundation (grant no. 175529).