© Springer Nature Switzerland AG 2020
M. La Rocca et al. (eds.)Nonparametric StatisticsSpringer Proceedings in Mathematics & Statistics339https://doi.org/10.1007/978-3-030-57306-5_7

A Kernel Goodness-of-fit Test for Maximum Likelihood Density Estimates of Normal Mixtures

Dimitrios Bagkavos1   and Prakash N. Patil2
(1)
Department of Mathematics, University of Ioannina, 45100 Ioannina, Greece
(2)
Department of Mathematics and Statistics, Mississippi State University, Starkville, Mississippi, USA
 
 
Dimitrios Bagkavos
Email: dimitrios.bagkavos@gmail.com

Abstract

This article contributes a methodological advance so as to help practitioners decide in selecting between parametric and nonparametric estimates for mixtures of normal distributions. In order to facilitate the decision, a goodness-of-fit test based on the integrated square error difference between the classical kernel density and the maximum likelihood estimates is introduced. Its asymptotic distribution under the null is quantified analytically and a hypothesis test is then developed so as to help practitioners choose between the two estimation options. The article concludes with an example which exhibits the operational characteristics of the procedure.

Keywords
Goodness-of-fitNormal mixturesKernel smoothing

1 Introduction

The choice between parametric and nonparametric density estimates is a topic frequently encountered by practitioners. The parametric (maximum likelihood, ML) approach is a natural first choice under strong evidence about the underlying density. However, estimation of normal mixture densities with unknown number of mixture components can become very complicated. Specifically, misidentification of the number of components greatly impairs the performance of the ML estimate and acts incrementally to the usual convergence issues of this technique, e.g., [11]. A robust nonparametric alternative, immune to the above problems is the classical kernel density estimate (kde).

The purpose of this work is to investigate under which circumstances one would prefer to employ the ML or the kde. A goodness-of-fit test is introduced based on the Integrated Squared Error (ISE) which measures the distance between the true curve and the proposed parametric model. Section 2 introduces the necessary notation and formulates the goodness-of-fit test. Its asymptotic distribution is discussed in Sect. 3 together with the associated criteria for acceptance or rejection of the null. An example is provided in Sect. 4. All proofs are deferred to the last Section.

2 Setup and Notation

Let $$\phi $$ denote the standard normal density and $$\phi _\sigma (x) = \sigma ^{-1} \phi (x \sigma ^{-1})$$ its scaled version. Let $$\varvec{\mu }= (\mu _1, \dots , \mu _k)$$ where for each $$\mu _i \in \varvec{\mu }$$, $$-\infty< \mu _i < +\infty $$ and $$\varvec{\sigma }= (\sigma _1, \dots , \sigma _k)$$ where each $$\sigma _i>0$$. Let also $$\textit{\textbf{w}} = (w_1, w_2, \dots , w_k)$$ be a vector of positive parameters summing to one. The finite positive integer k denotes the number of mixing components. Then,
$$\begin{aligned} f(x; \varvec{\mu , \sigma , w}) = \sum _{l=1}^k w_l \phi _{\sigma _l}(x- \mu _l) \end{aligned}$$
(1)
is a normal mixture density with location parameter $$\varvec{\mu }$$, scale parameter $$\varvec{\sigma }$$, and mixing parameter $$\textit{\textbf{w}}$$. The number of mixing components k is estimated prior and separately to estimation of $$(\varvec{\mu , \sigma , w})$$. Thus it is considered as a fixed constant in the process of ML estimation. Popular estimation methods for k include clustering as in [14] or by multimodality hypothesis testing as in [6] among many others. Regarding $$\varvec{\mu , \sigma , w}$$, these are considered to belong to the parameter space $$\Omega $$ defined by
$$\begin{aligned} \Omega = \left\{ \varvec{\mu }, \varvec{\sigma }, \textit{\textbf{w}}: \sum _{i=1}^k w_i = 1, w_i \ge 0, \mu _i \in \mathbb R, \sigma _i \ge 0 \text { for } i =1,\dots , k \right\} . \end{aligned}$$
The analysis herein assumes that all estimates are based on a random sample $$X_1, X_2, \dots , X_n$$ from $$f(x; \varvec{\mu , \sigma , w})$$. The parametric MLE is denoted by
$$\begin{aligned} \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) = \sum _{l=1}^{k} \hat{w}_l \phi _{\hat{\sigma }_l}(x- \hat{\mu }_l) , \end{aligned}$$
(2)
where $$(\varvec{ \hat{\mu }, \hat{\sigma }, \hat{w}})$$ denote the estimates of $$(\varvec{ \mu , \sigma , w})$$ resulting by maximization of
$$\begin{aligned} l(\varvec{\mu , \sigma , w}) = \sum _{i=1}^n \log \left\{ \sum _{j=1}^k w_l\phi _{\sigma _l}(X_i- \mu _l) \right\} , \end{aligned}$$
(3)
subject to $$(\varvec{ \mu , \sigma , w}) \in \Omega $$. Direct estimation of the density parameters by maximum likelihood is frequently problematic as (3) is not bounded on the parameter space, see [3]. In spite of this, statistical theory guarantees that one local maximizer of the likelihood exists at least for small number of mixtures, e.g., [8] for $$k=2$$. Moreover this maximizer is strongly consistent and asymptotically efficient. Several local maximizers can exist for a given sample, and the other major maximum likelihood difficulty is in determining when the correct one has been found. Obviously all these issues, i.e., correct estimation of k, existence and identification of an optimal solution for (3), result in the ML estimation process to perform frequently poorly in practice. A natural alternative is the classical kernel estimate of the underlying density which is given by
$$\begin{aligned} \hat{f}(x; h) = (nh)^{-1}\sum _{i=1}^n K \left\{ (x-X_i)h^{-1}\right\} , \end{aligned}$$
(4)
where h called bandwidth controls the amount of smoothing applied to the estimate and K, called kernel, is a real function integrating to 1. Attention here is restricted to second-order kernels as from [10], and it is known that using higher order kernels bears little improvement for moderate sample sizes. In estimating $$f(x; \varvec{ \mu , \sigma , w})$$ by $$\hat{f}(x;h)$$, especially when $$K=\phi $$, the MISE of the estimate can be quantified explicitly. The purpose of this research is to develop a goodness-of-fit test for
$$\begin{aligned} H_0: f(x) = f(x; \varvec{\mu , \sigma , w}) \text { vs } H_1: f(x) \ne f(x; \varvec{\mu , \sigma , w}). \end{aligned}$$
Its construction is based on the integrated square error of $$f(x; \varvec{\tilde{\mu }, \tilde{\sigma }, \tilde{w}})$$ given by
$$\begin{aligned} I_n = \int \left( f(x) - f(x; \varvec{\tilde{\mu }, \tilde{\sigma }, \tilde{w}}) \right) ^2\,\mathrm{d}x, \end{aligned}$$
where $$\{\varvec{ \mu , \sigma , w}\} =\{\varvec{ \tilde{\mu }, \tilde{\sigma }, \tilde{w}}\} $$ under $$H_0$$. Estimation of f(x) by a kernel estimate and $$f(x; \varvec{\tilde{\mu }, \tilde{\sigma }, \tilde{w}})$$ by $$\hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})$$ yields the estimate, $$\hat{I}_n$$ of $$I_n$$, defined by
$$\begin{aligned} \hat{I}_n&= \int \left( \hat{f}(x;h) - f(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})\right) ^2\,dx \nonumber \\&\equiv \int \hat{f}^2(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) \,\mathrm{d}x - 2 \int \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})\hat{f}(x;h) \,dx + \int \hat{f}^2(x;h)\,\mathrm{d}x . \end{aligned}$$
(5)
For $$K=\phi $$ by Corollary 5.2 in [1],
$$\begin{aligned} \int \hat{f}^2(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) \,dx = \sum _{l=1}^{ k} \sum _{r=1}^{ k} \hat{w}_l \hat{w}_r \phi _{(\hat{\sigma }_l^2 +\hat{\sigma }_r^2)^{\frac{1}{2} }}( \hat{\mu }_l - \hat{\mu }_r).\end{aligned}$$
(6)
$$\begin{aligned} \int \hat{f}^2(x; h)\,dx = \int \left\{ (nh)^{-1}\sum _{i=1}^n \phi (x-X_i) \right\} ^2 \,dx = (nh)^{-2} \sum _{i=1}^n \sum _{j=1}^n \phi _{\sqrt{2}}( X_i - X_j). \end{aligned}$$
(7)
Similarly,
$$\begin{aligned} \int \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) \hat{f}(x;h)\,dx = (nh)^{-1}\sum _{i=1}^n \sum _{l=1}^{k} \phi _{(\hat{\sigma }_l^2+1)^\frac{1}{2}} ( X_i - \mu _l) . \end{aligned}$$
(8)
Using (6), (7), and (8) back to (5) gives
$$\begin{aligned} \hat{I}_n&= \sum _{l=1}^{ k} \sum _{r=1}^{ k} \hat{w}_l \hat{w}_r \phi _{(\hat{\sigma }_l^2 +\hat{\sigma }_r^2)^{\frac{1}{2} }}( \hat{\mu }_l - \hat{\mu }_r) - 2 (nh)^{-1}\sum _{i=1}^n \sum _{l=1}^{k} \phi _{(\hat{\sigma }_l^2+1)^\frac{1}{2}} ( X_i - \hat{\mu }_l) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad + (nh)^{-2} \sum _{i=1}^n \sum _{j=1}^n \phi _{\sqrt{2}}( X_i - X_j), \end{aligned}$$
(9)
which is an equivalent expression for $$\hat{I}_n$$ that does not require integration.

3 Distribution of $$\hat{I}_n$$ Under the Null

This section establishes the null distribution of the test statistic $$I_n$$. First, the following assumptions are introduced,
  1. 1.

    $$h\rightarrow 0$$ and $$nh^2 \rightarrow +\infty $$ as $$n\rightarrow +\infty $$.

     
  2. 2.

    The density $$f(x; \varvec{\mu , \sigma , w})$$ and its parametric estimate $$\hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})$$ are bounded, and their first two derivatives exist and are bounded and uniformly continuous on the real line.

     
  3. 3.
    Let $$\textit{\textbf{s}}$$ be any of the estimated vectors $$\varvec{\mu , \sigma , w}$$ and let $$\varvec{\hat{s}}$$ denote its estimate. Then, there exists a $$\textit{\textbf{s}}^*$$ such that $$\textit{\textbf{s}} \rightarrow \textit{\textbf{s}}^*$$ almost surely and
    $$\begin{aligned} {\textit{\textbf{s}}} - \textit{\textbf{s}}^*= n^{-1} A(\textit{\textbf{s}}^*) \sum _{i=1}^n D \log f(X_i; \textit{\textbf{s}}^*) + o_p(n^{-1/2}) \end{aligned}$$
    where $$D \log f(X_i; \textit{\textbf{s}}^*) $$ is a vector of the first derivatives of $$\log f(X_i; \textit{\textbf{s}}^*) $$ with respect to $$s_j$$ and evaluated at $$s_j^*$$ while
    $$\begin{aligned} A(\textit{\textbf{s}}^*) = \mathbb E \left( \frac{\partial ^2 \log f(X_i; \textit{\textbf{s}}^*) }{\partial s_j \partial s_j'} \Big |_{ \textit{\textbf{s}} = \textit{\textbf{s}}^*}\right) . \end{aligned}$$
     
Theorem 1
Under assumptions 1–3 and under the null hypothesis,
$$\begin{aligned} d(n)\left( \hat{I}_n - c(n) \right) \rightarrow {\left\{ \begin{array}{ll} (\sigma _1^2 - \sigma _{30}^2)^\frac{1}{2} Z &{} \text { if } \;\; nh^5 \rightarrow \infty \\ 2^{1/2}\sigma _2 Z &{} \text { if } \;\; nh^5 \rightarrow 0\\ \left\{ \lambda ^{\frac{1}{2}}(\sigma _1^2 - \sigma _{30}^2)\lambda ^\frac{4}{5} + 2\lambda ^{-\frac{1}{5}} \sigma _2^2 \right\} ^\frac{1}{2} Z &{} \text { if } \;\;nh^5 \rightarrow \lambda \end{array}\right. } \end{aligned}$$
(10)
with $$0<\lambda <+\infty $$,
$$\begin{aligned} c(n)&= \frac{1}{nh}\frac{1}{2\sqrt{\pi }} + \frac{h^4}{4} \left\{ \sum _{l=1}^k\sum _{r=1}^k w_lw_r \phi _{(\sigma _l^2+\sigma _r^2 )^\frac{1}{2}}^{(4)}(\mu _l- \mu _r) \right\} +o(h^4)\\ \sigma _1^2&= \int \{ f''(x)\}^2 f(x)\,dx - \left\{ \int f''(x) f(x)\,dx\right\} ^2 = \mathrm {Var}\{f''(x)\}\\ \sigma _2^2&= \frac{1}{2 \sqrt{2\pi }}\sum _{l=1}^k \sum _{r=1}^k w_lw_r \phi _{(\sigma _l^2 +\sigma _r^2)^{\frac{1}{2} }}( \mu _l - \mu _r) \\ \sigma _{30}^2&= \sigma _{30}^2(\varvec{\mu , \sigma , w}) = \left[ \int D'f_0(x,\varvec{\mu , \sigma , w})f''(x)\,dx \right] A(\varvec{\mu , \sigma , w})^{-1} \\&\phantom { = \sigma _{30}^2(\varvec{\mu , \sigma , w}) =} \times \left[ \int Df_0(x,\varvec{\mu , \sigma , w})f''(x)\,dx \right] \end{aligned}$$
and
$$\begin{aligned} d(n) = {\left\{ \begin{array}{ll} nh^{1/2} &{} \text { if } nh^5 \rightarrow 0 \\ n^{1/2}h^{-2} &{} \text { if } nh^5 \rightarrow +\infty \\ n^{9/10} &{} \text { if } nh^5 \rightarrow \lambda \ne 0. \end{array}\right. } \end{aligned}$$
Thus, in testing $$H_0$$ against $$H_1$$ with significance level $$\alpha $$ we have
$$\begin{aligned} \hat{I}_n/\sqrt{\mathbb V \mathrm {ar}(\hat{I}_n)} \rightarrow N(0,1), \end{aligned}$$
where
$$\begin{aligned} \mathbb V \mathrm {ar}(\hat{I}_n) = {\left\{ \begin{array}{ll} \sigma _1^2 - \sigma _{30}^2 &{} \text { if } \;\; nh^5 \rightarrow \infty \\ (2^{1/2}\sigma _2 )^2 &{} \text { if } \;\; nh^5 \rightarrow 0\\ \lambda ^{\frac{1}{2}}(\sigma _1^2 - \sigma _{30}^2)\lambda ^\frac{4}{5} + 2\lambda ^{-\frac{1}{5}} \sigma _2^2 &{} \text { if } \;\;nh^5 \rightarrow \lambda . \end{array}\right. } \end{aligned}$$
Consequently, the test suggests rejection of $$H_0$$ when
$$\begin{aligned} \hat{I}_n \left\{ \mathbb V \mathrm {ar}(\hat{I}_n) \right\} ^{-1/2}>z_{\alpha }, \end{aligned}$$
where $$z_\alpha $$ is the standard normal quantile at level $$\alpha $$. Of course rejection of $$H_0$$ advises for using a kernel estimate instead of (2) for estimation of the underlying density.
../images/461444_1_En_7_Chapter/461444_1_En_7_Fig1_HTML.png
Fig. 1

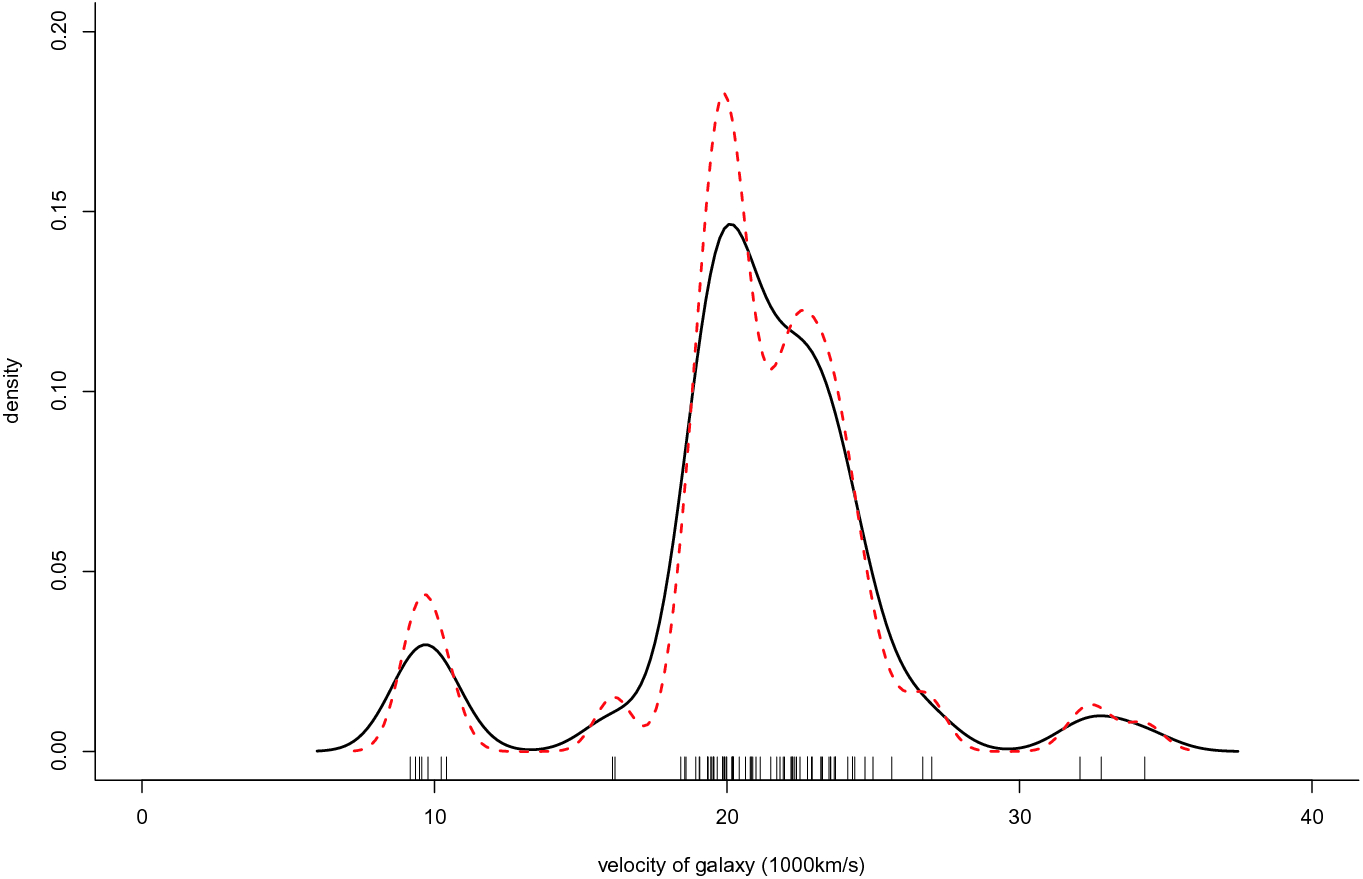
Variable bandwidth and ML estimates for the Galaxies data

4 An Example

As an illustrative example, the Galaxies data of [14] are used. The data represent velocities in km/sec of 82 galaxies from 6 well-separated conic sections of an unfilled survey of the Corona Borealis region. Multimodality in such surveys is evidence for voids and superclusters in the far universe.

The hypothesis that $$k=6$$ is also verified by the multimodality test of [6] and thus it is adopted in the present example as well. Figure 1 contains the ML (solid line) and kernel (dashed red line) estimates after scaling the data by 1000. The null hypothesis of goodness-of-fit of the ML estimate was tested at 5% significance level, using as variance the third component of the variance expression. The test procedure gives
$$\begin{aligned} \hat{I}_n \left\{ \mathbb V \mathrm {ar}(\hat{I}_n) \right\} ^{-1/2} = 1.98 >z_{0.95} = 1.64 \end{aligned}$$
and therefore suggests rejection of the null. This is also supported by Fig. 1 where it is seen that two distinctive patterns around $$x=18$$ and $$x=24$$ (and one less distinctive at around $$x=28)$$ are masked by the ML estimate. On the contrary, the fixed bandwidth estimate $$\hat{f}(x; h)$$ implemented with the Sheather–Jones bandwidth can detect the change in the pattern of the density. It is worth noting that the variable bandwidth estimate $$\tilde{f}(x)$$ has also been tested with the specific data set and found to perform very similarly to $$\hat{f}(x;h)$$.

5 Proof of Theorem 1

Write
$$\begin{aligned} \hat{I}_n&= \int \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - \hat{f}(x;h) \right\} ^2\,dx\nonumber \\&= \int \left\{ \hat{f}(x; \varvec{\mu , \sigma , w}) - f(x; \varvec{\mu , \sigma , w}) + f(x; \varvec{\mu , \sigma , w})- \hat{f}(x; h) \right\} ^2\,\mathrm{d}x\nonumber \\&= \int \left\{ \hat{f}(x;h) - f(x; \varvec{ \mu , \sigma , w}) \right\} ^2\,\mathrm{d}x \nonumber \\&\phantom {=} -2 \int \left\{ \hat{f}(x;h) - f(x; \varvec{\mu , \sigma , w}) \right\} \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x\nonumber \\&\phantom {=}+ \int \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - f(x; \varvec{\mu , \sigma , w}) \right\} ^2\,\mathrm{d}x \nonumber \\&\equiv I_1 - 2I_2 + I_3. \end{aligned}$$
(11)
Now, under $$H_0$$,
$$\begin{aligned} I_3&= \int \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - f(x; \varvec{\mu , \sigma , w}) \right\} ^2\,\mathrm{d}x \nonumber \\&= \int \Bigg \{\sum _{i=1}^k \frac{ w_i}{2 \sigma _i^3} \Bigg [ (x- \mu _i)^2 - (x- \hat{\mu }_i)^2 \Bigg ] (1+o_p(n^{-1}))\Bigg \}^2\,\mathrm{d}x = o_p(n^{-1}), \end{aligned}$$
(12)
since under the null the parameters of the normal converge to the true values. Also,
$$\begin{aligned} I_2&= \int \left\{ \hat{f}(x;h) - f(x; \varvec{\mu , \sigma , w}) \right\} \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})- f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x\nonumber \\&= \int \left\{ \hat{f}(x;h) - f(x; \varvec{\mu , \sigma , w}) \right\} \left\{ \mathbb E \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x + o_p(n^{-1}) \nonumber \\&\equiv J_{2} + o_p(n^{-1}). \end{aligned}$$
(13)
In (13), we used that under the null
$$\begin{aligned} \sup _x| \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})- \mathbb E \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}})| = o_p(n^{-1}). \end{aligned}$$
Thus, using (12) and (13) back to (11) yields the asymptotically equivalent expression for $$I_n$$
$$\begin{aligned} \hat{I}_n \equiv I_1 -2J_2 + o_p(n^{-1}). \end{aligned}$$
(14)
Now,
$$\begin{aligned} I_1&= \int \left\{ \hat{f}(x; h) - \mathbb E\hat{f}(x;h) +\mathbb E\hat{f}(x;h) - f(x; \varvec{\mu , \sigma , w}) \right\} ^2\,\mathrm{d}x \nonumber \\&= (nh)^{-2}\sum _{i=1}^n \sum _{j=1}^n H(X_i, X_j) + \frac{h^4}{4}\mu _2(K)R(f'') \nonumber \\&\phantom {=} -2 \int \left\{ \hat{f}(x; h) - \mathbb E\hat{f}(x; h) \right\} \left\{ \mathbb E\hat{f}(x; h)- f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x \end{aligned}$$
(15)
after using the squared bias expression of $$\hat{f}$$ from [10], and
$$\begin{aligned} H(X_i, X_j) = \\ \int \left\{ K\left( \frac{x-X_i}{h}\right) - \mathbb E K\left( \frac{x-X_i}{h}\right) \right\} \left\{ K\left( \frac{x-X_j}{h}\right) - \mathbb E K\left( \frac{x-X_j}{h}\right) \right\} \,\mathrm{d}x. \end{aligned}$$
Using the fact that K is a symmetric kernel and separating out the diagonal terms in the double sum in (15) we can write
$$\begin{aligned} (nh)^{-2}\sum _{i=1}^n \sum _{j=1}^n H(X_i, X_j) = (nh)^{-2}\underset{1\le i <j \le n}{\sum \sum } H(X_i, X_j) + (nh)^{-1}R(K) . \end{aligned}$$
(16)
By (15) and (16),
$$\begin{aligned} I_{1n} - \frac{h^4}{4}\mu _2(K)R(f'')-\frac{1}{nh}R(K) \equiv I_{1n} - c(n) = (nh)^{-2}\sum _{i=1}^n \sum _{j=1}^n H(X_i, X_j)\end{aligned}$$
(17)
$$\begin{aligned} -2 \int \left\{ \hat{f}(x;h ) - \mathbb E\hat{f}(x; h) \right\} \left\{ \mathbb E\hat{f}(x; h)- f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x . \end{aligned}$$
(18)
Combining (14) and (18) and rearranging yields
$$\begin{aligned} \hat{I}_{n} -c(n) = (nh)^{-2}\underset{i < j}{\sum \sum } H(X_i, X_j) \end{aligned}$$
(19)
$$\begin{aligned} +2 \int \left[ \left\{ \hat{f}(x;h ) - \mathbb E\hat{f}(x; h) \right\} - \left\{ \hat{f}(x; \varvec{\hat{\mu }, \hat{\sigma }, \hat{w}}) - f(x; \varvec{ \mu , \sigma , w}) \right\} \right] \times \end{aligned}$$
(20)
$$\begin{aligned} \left\{ \mathbb E\hat{f}(x; h)- f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x \end{aligned}$$
(21)
$$\begin{aligned} = 2 (nh)^{-2} \underset{i < j}{\sum \sum } H(X_i, X_j) +2k_2h^2n^{-1}\sum _{i=1}^n Z_i , \end{aligned}$$
(22)
where $$Z_i$$ is a term (see [5]) such that
$$\begin{aligned} h^2n^{-1}\sum _{i=1}^n Z_i = O_p(h^2 n^{-1/2}). \end{aligned}$$
Moreover, under the null and when $$nh^5\rightarrow \infty $$, this term determines the limiting distribution of the right-hand side of (22). Now, under the null, the fact that
$$\begin{aligned} \sqrt{n}h^{-2}\int \left\{ \hat{f}(x; h) - \mathbb E\hat{f}(x; h) \right\} \left\{ \mathbb E\hat{f}(x; h)- f(x; \varvec{\mu , \sigma , w}) \right\} \,\mathrm{d}x \rightarrow k_2\sigma _1 Z \end{aligned}$$
is a standard result. Taking into account that $$d(n)=n^{1/2}h^{-2}$$ and by applying the Lyapunov Central Limit Theorem yields
$$\begin{aligned} n^{1/2} \sum _{i=1}^n Z_i \rightarrow N(0, \sigma _1^2 - \sigma _{30}^2) \end{aligned}$$
which proves the first leg of (10). For proving the second leg, we have that under the null and for $$nh^5\rightarrow 0$$, $$d(n)=n\sqrt{h}$$. In this case
$$\begin{aligned} h^2n^{-1}\sum _{i=1}^n Z_i = O_p( (n h^5)^{1/2}) = o_p(1). \end{aligned}$$
Hence the limit distribution of $$d(n)(I_n - c(n))$$ has the same distribution as the first term on the right-hand side of (22). By a direct application of Theorem 1 of [7] and taking into account also the proof of Theorem 3.2 in [5], it is straightforward to deduce that
$$\begin{aligned} n\sqrt{h}\left\{ (nh)^{-2}\underset{1\le i <j \le n}{\sum \sum } H(X_i, X_j) \right\}&\rightarrow \sqrt{2}\sigma _2 Z\end{aligned}$$
, and thus establish the middle part on the right-hand side of (10). For the remaining part of (10), note that when $$nh^5\rightarrow \lambda , d(n) = n^{9/10}$$ and hence no term on the right-hand side of (22) dominates the other since both are of the same order. Therefore, in this case, the limiting distribution of $$d(n)(I_n - c(n))$$ is given by the sum of the limit distribution of the two terms since, both terms are uncorrelated to each other.