XII
Zeno: Paradox and Plurality

(a) The Eleatic Palamedes

According to Coleridge, ‘the few remains of Zeno the Eleatic, his paradoxes against the reality of motion, are mere identical propositions spun out into a sort of whimsical conundrums’. Depreciatory judgments of that character excited a splendid retort from Russell: ‘In this capricious world, nothing is more capricious than posthumous fame. One of the most notable victims of posterity’s lack of judgment is the Eleatic Zeno. Having invented four arguments, all immeasurably subtle and profound, the grossness of subsequent philosophers pronounced him to be a mere ingenious juggler, and his arguments to be one and all sophisms.’¹

Philosophers have been driven to repentance by Russell’s lashes. Zeno now stands as the most celebrated of Presocratic thinkers; and his paradoxes are again vivacious philosophical issues. Yet of Zeno himself our knowledge is exiguous: the surviving fragments count barely two hundred words; the doxography is slight and repetitious; and the structure and impetus of Zeno’s thought remain dark and controversial.

We know surprisingly little of Zeno’s life and history;² and most of our information comes from the celebrated but suspect story in Plato’s Parmenides. The passage is worth quoting at length; Pythodorus is describing the visit of Parmenides and Zeno to Athens:

…They came to Athens, as he said, at the great Panathenaea: the former was, at the time of his visit, about 65 years old, very white with age, but well favoured. Zeno was nearly 40 years of age, tall and fair to look upon: in the days of his youth he was reported to have been beloved by Parmenides. He said that they lodged with Pythodorus in the Ceramicus, outside the wall, whither Socrates, then a very young man, came to see them, and many others with him: they wanted to hear the writings of Zeno, which had been brought to Athens for the first time on the occasion of their visit. These Zeno himself read to them in the absence of Parmenides, and had very nearly finished when Pythodorus entered, and with him Parmenides and Aristoteles who was afterwards one of the Thirty, and heard the little that remained of the dialogue. Pythodorus had heard Zeno repeat them before.

When the recitation was completed, Socrates requested that the first thesis of the first argument might be read over again, and this having been done, he said: What is your meaning, Zeno? Do you maintain that if entities are many, they must be both like and unlike, and that this is impossible, for neither can the like be unlike, nor the unlike like—is that your position?

Just so, said Zeno.

And if the unlike cannot be like, or the like unlike, then according to you, entities could not be many; for this would involve an impossibility. In all that you say have you any other purpose except to disprove the existence of the many? and is not each division of your treatise intended to furnish a separate proof of this, there being in all as many proofs of the non-existence of the many as you have composed arguments? Is that your meaning or have I misunderstood you?

No, said Zeno; you have correctly understood my general purpose.

I see, Parmenides, said Socrates, that Zeno would like to be not only one with you in friendship but your second self in his writings too: he puts what you say in another way, and would fain make believe that he is telling us something which is new. For you, in your poems, say The All is one, and of this you adduce excellent proofs; and he on the other hand says there is no many: and on behalf of this he offers overwhelming evidence. You affirm unity, he denies plurality. And so you deceive the world into believing that you are saying different things when really you are saying much the same. This is a strain of art beyond the reach of most of us.

Yes, Socrates, said Zeno. But although you are as keen as a Spartan hound in pursuing the track, you do not fully apprehend the true motive of the composition, which is not really such an artificial work as you imagine; for what you speak of was an accident; there was no pretence of a great purpose: nor any serious intention of deceiving the world. The truth is that these writings of mine were meant to protect the arguments of Parmenides against those who make fun of him and seek to show the many ridiculous and contradictory results which they suppose to follow from the affirmation of the one. My answer is addressed to the partisans of the many, whose attack I return with interest by retorting upon them that their hypothesis of the existence of many, if carried out, appears to be still more ridiculous than the hypothesis of the existence of one. Zeal for my master led me to write the book in the days of my youth, but someone stole the copy: and therefore I had no choice whether it should be published or not: the motive, however, of writing was not the ambition of an elder man, but the pugnacity of a young one. This you do not seem to see, Socrates; though in other respects, as I was saying, your notion is a very just one.

I understand, said Socrates, and quite accept your account (172:127A-128E, trans. Jowett).

The details of the story, and the chronology implicit in it, are not my concern. What matters is the central core of Plato’s account, which most scholars accept as historical truth. According to that core, Zeno in his youth, incensed by the ignorant attacks on his master’s monism, wrote a collection of arguments designed to reduce pluralism to absurdity and so to defend monism. The story thus ascribes a plan, an aim and a method to Zeno; let us take them in turn.

Zeno’s tract contained many arguments (127E). Proclus, in his commentary on the Parmenides, says that there were forty logoi in all (29 A 15; so too Elias, A 15); and there is no reason to reject his testimony. All those logoi attacked the hypothesis of pluralism: of the eight Zenonian arguments that we possess, two certainly were numbered among those forty. The standing of the four paradoxes on motion is uncertain: they can be pressed into a suitable form for membership of the forty; but Elias (A 15) says that in addition to the forty logoi there were five arguments against motion.³ Moreover, it is clear from Aristotle’s account that the paradoxes of motion were customarily treated as a special unity; and that may reflect a special origin. For the rest, antiquity supplies four Zenonian book-titles;⁴ but they do not enable us to say anything about the original format of Zeno’s publications.

Some scholars are not content with the information that Zeno’s tract contained forty logoi: they attempt to discern a grand architectonic structure uniting several of the logoi into a complex and sophisticated argument against pluralism. Thus Zeno is bent on attacking pluralism: if the world is divisible into parts, then it is finitely or infinitely divisible; if finitely divisible, then its parts are separated by other bodies or by gaps (which B 3 rules out), or else they abut one another (which the Arrow rules out); if infinitely divisible, then either the division is completable (which B 2 rules out) or it is not (which the Dichotomy and the Achilles rule out). By a happy chance, the logoi we possess form a single integrated construction.⁵

Such architectonic interpretations have a certain attraction. But closer inspection reveals gaps and botches in the building: if Zeno did build thus, he was not a particularly skilful builder. Moreover, those interpretations are wholly products of the scholarly fancy. There is not a jot of evidence in any ancient text that Zeno’s logoi ever formed such an integrated and interdependent whole; no ancient author knows anything of Zeno the logical master-builder. On the contrary, there is some evidence against the interpretation; for Plato asserts that each logos itself constituted a proof against pluralism. And if the fragments and reports of Zeno’s arguments have been supposed to suggest an overall structure, that supposition is, in my view, quite illusory; and my discussion of the paradoxes will give no hint of a systematic interdependence among Zeno’s different arguments.

So much for the plan of Zeno’s arguments. Their aim, according to the Parmenides, was to defend Parmenides against those who were attempting to make fun of him (128C). Modern scholars have tried to identify those anonymous mockers, but without success. Many have invoked the Pythagoreans: a curious philosophy, called ‘unit-pointatomism’, has been ascribed to the sect; the philosophy has been judged a consciously anti-Parmenidean invention; and Zeno’s arguments have then been interpreted as a rejection of the philosophy and hence as a defence of Parmenides. But that account is the merest fantasy: ‘unit-point-atomism’, if it existed, would not constitute a peculiarly incisive and mocking rejection of Parmenides; it is pluralistic, but so is every non-Eleatic theory. And in any case, the doctrine never existed: there is no direct evidence for it; and in order to infer its existence from Zeno’s paradoxes we must subject those arguments to a gratuitously tortuous interpretation. For many years scholars have campaigned for and against a Pythagorean opposition to Parmenides; by now the campaign should be over.⁶

Did Zeno defend Parmenides against philosophical attack from some other quarter? I doubt it. Plato implies that the attacks on Parmenides were satirical rather than philosophical, and the Eleatic position is an obvious target for satire and ridicule. We can be sure that Parmenides, like all later metaphysicians of any originality, was an object of popular mirth: where his doctrines were known—or half-known—they will have been jeered at. It is to such receptions, and not to philosophical opposition, that Plato refers.⁷

Was it Zeno’s aim to defend Parmenides against mockery? I am inclined to doubt Plato’s suggestion that it was. First, I doubt that Parmenides was a monist at all. Second, even in the Parmenides Zeno does not claim to have been defending monism in any straight-forward way. He asserts that the defence of monism which Socrates has read into his logoi was only incidental; his aim was to show that pluralism suffers ‘still greater absurdities’ than monism. That is hardly the language of an ardent monist. Third, even if pluralism is absurd, monism is not thereby defended; Plato is wrong in saying that a proof of monism and a refutation of pluralism come to the same thing. Zeno’s pupil Gorgias was well aware of that: he was, notionally at least, a nihilist.⁸ Fourth, more than one of Zeno’s arguments seem to bear with equal force against pluralism and against monism. I shall note these cases as I discuss the paradoxes; here I observe that they make it hard to envisage Zeno as a self-conscious monist.

Those considerations seem to be supported by a strand in the doxographical tradition. The thesis that Zeno attacked ‘the One’ is discussed, and rejected, by Simplicius (in Phys 97.9–99–3; 138.3–139.23); and it originated with Eudemus.⁹ Unfortunately, Eudemus offered only weak support for his opinion, citing an anecdote and preparing a collage of three Zenonian arguments. The arguments, as Simplicius observes, are taken from Zeno’s logoi against pluralism, and I shall consider them later; whatever their force, they do not reveal Zeno as a formal opponent of monism. The anecdote runs like this:

They say that Zeno used to say that if someone would tell him what on earth the one (to hen) is, he would be able to talk about the things that exist (173: Eudemus, fr. 37aW=A 16=L 5).¹⁰

Nothing can be based on this second-hand story: ‘to hen’ may, I suppose, mean ‘the [Eleatic] One’, and Zeno may have meant to cast doubt on its credentials; but ‘to hen’ may equally mean ‘a unit’, and refer to the units that construct the pluralist world.¹¹ Eudemus’ evidence does not establish that Zeno overtly attacked monism; but the four preceding considerations do at least show that he was not greatly concerned to defend it.

I turn to the question of Zeno’s logical method. In the Parmenides (127E), Socrates gets Zeno to agree that each of his arguments is intended to have the form of a reductio ad impossible; and later writers dutifully expound them in that form (cf. Proclus, A 15). Aristotle called Zeno the father of ‘dialectic’, and ‘dialectic’ may mean ‘logic’. Modern scholars often regard Zeno as the first self-conscious logician, or at least as the inventor of argument by reduction.¹²

A pinch of sceptical snuff will clear the mind. Zeno was not the first thinker to use reductio, nor was he the first logician to reflect upon reductio; others had argued reductively before Zeno, and no one studied logic before Aristotle. Moreover, it is improbable that Zeno himself used reductive arguments. Indeed Plato almost says as much; for he represents Socrates as extracting from Zeno the realization that his arguments are reductive and not as finding a reductive form in the logoi themselves. Socrates is bringing to fictional consciousness what was at best latent in historical reality. Zeno’s surviving fragments contain no reductio: he takes an hypothesis and infers an absurdity from it; but he never makes the characteristic move of reductio, the inference to the falsity of the hypothesis. He argues ‘If P, then Q’, where Q states some absurdity; but he does not explicitly infer the falsity of P. In other words, he does not use reductio ad absurdum as a technique for disproof. ₁₃

In the Parmenides Zeno presents himself, or at least his juvenile self,¹³ as an eristic debater, a sophist out to impress an audience; and in the Phaedrus he is called an antilogikos or logic-chopper.¹⁴ I do not suggest that Zeno was a charlatan, a purveyor of arguments which he knew to be fallacious; nor do I mean that he had no philosophical interest in Eleaticism. But I do suggest that Zeno was not a systematic Eleatic solemnly defending Parmenides against philosophical attack by a profound and interconnected set of reductive argumentations. Many men had mocked Parmenides: Zeno mocked the mockers. His logoi were designed to reveal the inanities and ineptitudes inherent in the ordinary belief in a plural world; he wanted to startle, to amaze, to disconcert. He did not have the serious metaphysical purpose of supporting an Eleatic monism; and he did not adopt a ponderous logical precision in his method.

That conclusion has some slight .importance. Many modern interpreters of Zeno have argued that such and such an account of a paradox is wrong because it attributes a silly fallacy to a profound mind. Zeno was not profound: he was clever. Some profundities did fall from his pen; but so too did some trifling fallacies. And that is what we should expect from an eristic disputant. If we meet a deep argument, we may rejoice; if we are dazzled by a superficial glitter, we are not bound to search for a nugget of philosophical gold. Fair metal and base, in roughly equal proportions, make the Zenonian alloy.

(b) Large and small

It is appropriate to begin with those of Zeno’s surviving arguments which specifically attack pluralism. They account for all that we possess of Zeno’s own words; they were certainly a part of his collection of logoi; and some of the issues they raise underlie the subtler paradoxes of motion.

The hypothesis under attack, pluralism, simply says that ‘there exist many things’. I shall abbreviate this to P. It is, I take it, a moderately clear and unambiguous hypothesis. If Zeno is out to show the absurdity of pluralism, we may expect his attacks on P to conclude to propositions of the form:

(Z*) If P, then Q and not-Q.

That is equivalent to:

(Z) If P, then Q; and if P, then not-Q,

and the surviving evidence shows that, in some cases at least, Zeno did set himself to demonstrate a conjunctive proposition of the form

(Z); and his procedure was the obvious one of arguing independently for each conjunct of the conjunction.¹⁵

According to the Phaedrus, Zeno made ‘the same things seem like and unlike, and one and many, and at rest and in motion’ (261D=A 13). To those three pairs of opposites we may add at least two others: large and small (B 1–2), and finite and infinite (B 3). Such pairs can all readily be accommodated to the schema (Z). Doubtless there were more pairs; but it is hardly likely that the forty arguments used forty distinct pairs of opposites.¹⁶

The first logos in Zeno’s treatise used the pair ‘like and unlike’ (172: Parm 127D-E). Zeno’s first conclusion, then, will have been:

(Z1) (a) If P, then everything is alike, and (b) if P, then everything is unlike.

We do not know how Zeno argued for (Z1), nor what he meant by ‘everything is alike’.¹⁷ The word for ‘alike’ is ‘homoios’. Perhaps: ‘If a and b are distinct existents, then they are similar (homoios) in so far as each exists—hence they are alike; and they are dissimilar (anhomoios) in so far as each is different from the other—hence they are unlike.’ Or perhaps rather: ‘If a and b are distinct existents, then as existent each will be homogeneous (homoios)—hence they are alike; and yet being distinct, they are heterogeneous and hence unlike’.

Neither argument has any power; for neither conclusion is more than an apparent absurdity: the consequents of (Z1) do not together amount to anything of the damning form ‘Q and not-Q’. The first argument is sound and harmless; the second, even if it were sound, would cause no pluralist any loss of sleep. For all that, it is worth starting with (Z1), for two reasons. First, it may finally kill the desire to find a subtle argument behind Zeno’s every dictum. Second, it exhibits an interesting feature of Zeno’s technique: P contains the two notions of existence and of plurality. In (Z1), conjunct (Z1a) makes use of the notion of existence in P, and conjunct (Z1b) turns to that of plurality. P is absurd (Zeno urges) because it conjoins two notions with contradictory implications.

I turn now to the logos of ‘large and small’; we know that it preceded the logos of ‘finite and infinite’ (Simplicius, in Phys 140.34), but we do not know its absolute position among the forty logoi. For this logos we possess some of Zeno’s own words. Simplicius, who preserves them, quotes them in the course of a piece of commentatorial controversy; and it is necessary to reconstruct the original argument from two passages in Simplicius’ text. Since scholars have not agreed on the reconstruction, I shall begin by displaying the two passages.¹⁸

In the first passage, Simplicius is concerned to refute the opinion of Alexander and Eudemus that Zeno ‘rejected the One’:

In the treatise of his which contains many arguments, he proves in each one that anyone who asserts that there exist many things is committed to asserting opposites. One of these is an argument in which he proves that [i] if there exist many things, they are both large and small—large so as to be unlimited in magnitude, small so as to have no magnitude. Now in this he proves that [ii] what has neither magnitude, nor mass, nor bulk, would not even exist. ‘ [iii] For’, he says, ’if it were attached to something else that exists, it would not make it larger; [iv] for if it is of no magnitude but is attached, that thing cannot increase at all in magnitude, [v] And in this way what is attached will thereby be nothing, [vi] And if, when it is detached, the other thing is no smaller, and, when it is attached again, it will not grow, it is clear that what is attached is nothing, and likewise what is detached.’ And Zeno says this not in order to reject the One, but [vii] to show that each of the many things has a magnitude—and an unlimited one at that (for there is always something in front of what is taken, because of the unlimited division). [viii] And he proves this having first proved that each of the many things has no magnitude from the fact that each is the same as itself and one (174: in Phys 139.5–19; cf. B2= 9L).¹⁹

In the second passage, which is part of the same long note on Physics 187a1, Simplicius is arguing against Porphyry’s view that the ‘dichotomy’ argument to which Aristotle refers belongs to Parmenides rather than to Zeno:

And why should we waste words when [the argument] is actually produced in Zeno’s own treatise? For in proving that if there exist many things the same things are unlimited and limited Zeno writes in these words: [ix] ‘If there exist many things, it is necessary that they be as many as they are and neither more than themselves nor less. But if they are as many as they are, they will be limited. If there exist many things, the things that exist are unlimited. For there are always other things in the middle of the things that exist, and again others in the middle of those. And thus the things that exist are unlimited.’ And in this way he proved their numerical unlimitedness from the dichotomy. Their quantitative unlimitedness [he proved] earlier by the same method of argument, [x] For having proved beforehand that if what exists had no magnitude it would not even exist, he continues: ‘[xi] and if there exist [many things], it is necessary for each to have a certain magnitude and mass, [xii] and for the one part of it to be separate from the other, [xiii] And the same argument holds of what protrudes; for that too will have a magnitude, and some part of it will protrude, [xiv] Now it is all one to say this of one case and to say it of every case; for no such part of it will be last, nor will there not be another part related to another.²⁰ [xv] Thus if there exist many things, it is necessary for them to be both small and large—so small that they have no magnitude, so large that they are unlimited’ (175: in Phys 140.27–141.8: cf. B3=11L; B1=10 L).

Sentence [ix] (=B 3) contains the logos of ‘finite and infinite’; since it appeared in Zeno’s treatise after the ‘large and small’, I shall postpone discussion of it. Sentence [x] shows that the argument in [xi]–[xiv] was preceded by the argument in [iii]–[vi]; and sentences [vii] and [viii] show that the argument in [xi]–[xiv] was preceded by the argument briefly retailed in [viii]. Simplicius does not state explicitly that the argument of [viii] preceded that of [iii]–[vi]; but the content of the two arguments, and the form of Zeno’s antinomy, make that precedence clear.

[i] and [xv] give the conclusion of the logos of ‘large and small’; it is striking:

(Z2) (a) If P, then everything has no magnitude, and (b) if P, then everything has infinite magnitude.

Given (Z2a), Zeno need only argue that everything has some positive magnitude; given (Z2b) he might rest content with a proof that everything has a finite magnitude: to urge both (Z2a) and (Z2b) is logically excessive; and Zeno’s urging is a tour de force.

Zeno’s argument for (Z2a) is given in sentence [viii]; the argument for (Z2b) is stated in [xi]–[xiv], and it is prepared for in [iii]–[vi]. These latter sentences argue for the lemma: (L) If a exists, then a has a positive magnitude.

Thus from Simplicius’ text we can reconstruct the following account of Zeno’s logos:

(Z2a)=[viii];

lemma (L)=[iii]–[vi],

whence (Z2b)=[xi]–[xiv]:

hence (Z2)=[xv].

I shall accordingly discuss the logos in the order (Z2a); (L); (Z2b).²¹

(c) Existence

(Z2a) need not detain us long. Zeno appears to have moved from ‘a is self-identical and one’ to ‘a is without magnitude’. Scholars mediate the move by ‘a is partless’, and refer to Melissus, 171, and to Plato’s Parmenides, 137CD.²² I have already commented briefly on this argument (above p. 227). I am not sure that it was Zeno’s (it makes no use of the premiss of self-identity); but I have no alternative to offer. It may be observed that the hypothesis, P, plays no pan in the derivation of (Z2a); as we shall see, P is similarly inactive in the derivation of (Z2b): the antinomy works impartially against P and against monism.

What of the argument for (L)? Some scholars feel that it prevaricates upon the word ‘nothing’²³ but I do not share the feeling, and I shall ignore Zeno’s use of the word in [v] and [vi]. The logical articulation of [iii]–[vi] is not wholly clear: if we use ‘a+b’ to mean ‘the result of attaching a to b’; and ‘mag: a’ for ‘the magnitude of a’, then [iii], I think, expresses the following proposition:

(1) If mag: a=0, then if b exists and a is attached to b then mag: a +b=mag: b.
As far as I can see, [iv] merely repeats [iii]. As for [v], that states:

(2) If, if b exists and a is attached to b, then mag: a+b=mag: b, then a does not exist.
[vi] repeats the matter of [v] and adds to it a parallel clause about ‘detachment’. I assume that [vi], which Aristotle calls ‘Zeno’s axiom’ (Met 1001b7=A 21), is an improved or completed version of [v]; a similarly improved version of [iii] is needed, if any inference is to be made from [vi]. (1) and (2) immediately yield:

(3) If mag: a=0, a does not exist.

If we make the harmless assumption that nothing can have a negative magnitude, then (3) yields (L).

Is (2), Zeno’s unimproved axiom, true? The words ‘prosgignesthai’ and ‘apogignesthai’, which I translate ‘be attached to’ and ‘be detached from’, are standardly rendered by ‘be added to’ and ‘be subtracted from’. That rendering gives encouragement to those who see a geometrical base to Zeno’s paradox and construe (L) as a theorem about geometrical points;²⁴ but it is mistaken: Zeno is thinking of the collocation and dislocation of physical objects; and ‘a +b’ denotes the complex object formed by juxtaposing, intermixing, fusing or otherwise uniting the two objects a and b. The term ‘magnitude’ in (2) is generally taken to mean ‘size’ or ‘volume’. It is apparent, then, that (2) is not a logical truth; indeed, it turns out to be a contingent falsehood. It plainly presupposes that, in general, mag: a+b=mag: a+mag: b; but that presupposition, as every schoolboy knows, is false: a pint of alcohol mixed with a pint of water does not yield a quart of liquor. Moreover, (2) itself, I am told, is false: one of the peculiarities of the stuff zeolite is that, when added to water, it does not increase the volume of the water: mag: z+w= mag: w.

Zeno might attempt to escape from this objection in either of two ways. First, he might abandon the physical interpretation of ‘attachment’ and tell us that it is, after all, a mathematical operation that he has in mind. Alternatively, he might prefer to have ‘magnitude’ understood as ‘mass’. (According to Simplicius, he uses megethos, pachos, and onkos indiscriminately.) On both readings, the presupposition that mag: a+b=mag: a+mag: b turns out true: on the first reading, it is a tautology; on the second, a primitive version of the Law of Conservation of Matter.

Yet neither of those defences will save Zeno. (2) carries a second, more general, presupposition, namely that if a is attached to b then a must be the sort of thing to have a magnitude—a volume or a mass, Surely, though, I can ‘attach’ my shadow to a wall, or ‘attach’ a picture to a cinema screen: shadows and pictures occupy no volume and have no mass; the shadowy wall and the coloured screen have precisely the same magnitude as the sunlit wall and the vacant screen; yet for all that cast shadows and projected pictures exist. And that appears to refute (2).

Aristotle anticipated and answered this objection: Zeno advances his axiom

clearly assuming that what exists is a magnitude—and if a magnitude, corporeal (sômatikon); for that is what exists in all ways [i.e. is three-dimensional] (176: Met 1001b9=A 21).

(2) holds only if a and b are three-dimensional physical objects: I
objected to (2) by citing cases in which a is a two-dimensional object; Aristotle suggests the simple retort: ‘restrict a and b to threedimensional objects’. It makes no odds whether we say that (2) is false but open to simple emendation; or rather that (2) is true when properly understood. The important fact is simply this: (2) is true if a and b are three-dimensional. And Zeno is surely entitled to that 11hypothesis: any pluralist will be proclaiming a world populated by fairly ordinary middle-sized objects; and it is such a pluralism that Zeno is out to attack. The commentators say as much in connexion with a later logos.

If (2) is true, so is (1); and thus Zeno has his conclusion. Moreover his conclusion need not decide between the two interpretations of ‘magnitude’; for three-dimensional physical objects—bodies, for short—have both volume and mass. But victory is won at a price; and the price is triviality. The lemma (L), which reads like a strong ontological thesis, asserting that only things with magnitude can exist, turns out on examination to state no more than the analytic truth that all existent bodies occupy space and have a positive mass. From (L) nothing follows about the ontological status of shadows, of numbers, of points, of abstract entities—or of anything else.

The triviality of (L) may prove unimportant; what matters is whether it can function in the main argument for (Z2b). Yet it is, in a sense, distressing: the argumentative apparatus in [iii]–[vi] seems singularly pointless if (L) is as trifling as I claim; and some may still think that Zeno has stronger meat to cook. I can only say that no stronger conclusion will emerge from [iii]–[vi]; that there is no positive harm in impressing the truth of (L) by what is, after all, a sound argument; and that the interest of (L) lies in any case in its application to (Z2b), an application to which I now turn.

(d) Infinite division

The argument in [xi]–[xiv] is peculiarly difficult to grasp; and my presentation will, I fear, be both laborious and unconfident. First, let me offer a somewhat more precise version of its component sentences.

Sentence [xi] says that ‘if there exist many things, it is necessary for each to have a certain magnitude and mass’; that, I assume, amounts to:

(1) If there exist objects a1, a2, . . ., an, then for each i, mag: ai>0.

That is simply an application of the lemma (L). Sentence [xii] reads: ‘. . . and for the one part of it to be separate from (apechein) the other’; i.e.:

(2) If a_i exists, then there exist distinct parts of ai, b, and c_i.

I assume that the word apechein connotes nothing stronger than distinctness: that assumption is all that Zeno needs. Sentence [xiii]—‘And the same argument holds of what protrudes’—applies (1) and (2) to one of the parts of ai, say bi. (I see no special significance in Zeno’s label, ‘what protrudes’.) And [xiv] asserts that (1) and (2) can be applied again to the parts of bi, to the parts of the parts of bi, and so on.

All that seems innocuous enough: how on earth are we to extract from it the lethal poison of (22b)? How can we generate, or seem to generate, infinitely large elephants from the little mice that play before us?

The rough answer to this question is not difficult to discover. By (2), every existent object contains infinitely many existent parts; and by (1) each of those parts has a positive magnitude. Now the magnitude of any object is equal to the sum of the magnitudes of its parts; and since any object has infinitely many parts, its magnitude is equal to the sum of the magnitudes of that infinity of parts. But the sum of infinitely many positive magnitudes is infinite; hence the magnitude of any object is infinite.

That, I think, is an uncontroversial expansion of Zeno’s argument. The only premiss it requires which is not found in the Greek text is the thesis that the sum of an infinite set of magnitudes is infinite; and all scholars agree that some such thesis must be ascribed to Zeno. But the argument is still imprecise and impressionistic. I shall now attempt a more rigorous presentation. The ferociously technical aspect of what follows is, I believe, indispensable: if an argument is worth stating, it is worth stating precisely; and I cannot find a less unattractive route to precision than the one I follow here.

First, I need the notion of a Zeno-set or Z-set. Roughly speaking, a Z-set of an object a is any collection of all its parts: four legs and a top are a Z-set of the table I write upon; a few hundred pages, a spine, and two boards are a Z-set of the book you are reading; take a motor-mower engine to bits and beside you on the lawn you will have, if you are fortunate, a Z-set of the engine. Formally:

(D) {x₁, x₂…, x_n} is a Z-set of y if and only if (a) every x, is a proper part of y, (b) no x_i is a part of any other xi, and (c) no part of y is not a part of the sum of all the x,s.

In place of Zeno’s premiss (1) we can employ the simpler:

(3) If a exists, then mag: a>0.

And in place of (2) we must use the more complex:

(4) If mag: a>0, then there is aZ-set of a, {x1, x2,…}, such that for every i mag: xi > 0.

A further premiss is now required:

(5) If {x₁₁, x₁₂,…} is a Z-set of x₁, and {x₁₁, x₂₂,…} is a Z-set of x₂, and . . . and {x_n1, x_n2…} is a Z-set of x_n, and {x₁, x₂,…x_n} is a Z-set of a, then {x₁₁, x₁₂,…x₂₁, x₂₂,…, …x_n1, x_n2…} is a Z-set of a.

That is formidable in appearance; but it only expresses, in formal dress, the mundane truth that any object is made up of the parts of its parts.

From (3)–(5) I infer:

(6) If a exists, then for any n there is a Z-set of a, {x₁, x₂,…, x_m}, such that m>n, For suppose that the most numerous Z-set of a is k, or {x₁, x₂,…, x_k}. Then mag: x_k>0, and hence there is a Z-set of x_k, say {x_k1, x_k2, …, x_kj}. But then there will be a Z-set of a {x₁, x₂,…, x_k–1, x_k1, x_k2,…, x_kj}; and that will be more numerous than k. Hence k is not the most numerous Z-set of a.

In effect, (6) says that a is infinitely divisible, or contains infinitely many parts. A further premiss, of self-evident truth, is now needed:

(7) If {x₁, x₂,…x_n,…} is a Z-set of a, then mag: a=mag: x₁+ mag: x₂+…+mag: x_n+… I use the sign 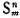to name the set {x_n, x_n+1,…,x_m}; and ‘’ for infinity. By (6), then, there is a Z-set of a ; and hence, by (7):

(8) If a exists, then mag: a=mag: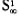

Finally, we need a premiss concerning the summing of infinite sets, viz:

(9) If for every x_i in mag: xi > 0, then mag: =
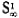
It is now a simple inference to:

(10) If a exists, mag: a=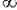
And (10) is equivalent to (Z2b).

Evidently, the argument is unsound; and it has found no serious defenders. Yet its opponents are in disarray, and there is no agreement on just where the flaws—or the chief flaws—are to be found. In the next section I shall discuss five objections against Zeno.

(e) The toils of infinity

First, and most obviously, Zeno’s opponents may deny (2) or (4): it is simply not true that every part of a has parts; it is simply not true that partition may continue ad infinitum. Physical bodies have minimal parts; and, being composed of a finite number of finite parts, they are felicitously finite in magnitude. In 174 and 175 Zeno is speaking of physical bodies: there is no reason to believe what he says in (2) and good reason to disbelieve it.²⁵

That atomistic answer has left most Zenonians unmoved. No doubt Zeno is talking of the physical parts of physical bodies; but he need not be construed as talking of physical operations of division or splitting. Behind the physical façade of proposition (2) there lies a mathematical substance; and (2) rests not upon false or dubious physical theory but on a truth of stereometry: every geometrical solid s has a Z-set {s1, s2,…} all of whose members are geometrical solids; and since the magnitude of a physical body is determined by the volume of the geometrical solid which its spatial co-ordinates describe, if the volume is infinitely large, so too is the magnitude.

Some Greek thinkers were moved by that argument to posit indivisible geometrical magnitudes: just as physical division stops somewhere, so, they supposed, geometrical division has a terminus. Xenocrates, a pupil of Plato’s, ‘gave in to this argument about the dichotomy and accepted that everything divisible is many…for he said that there are atomic lines of which it is no longer true that they are many’ (fr. 44 H=Simplicius, in Phys 138.10–6). Doubtless Xenocrates also postulated indivisible geometrical solids.²⁶ If a stereometrical atomism thus backs up physical atomism, premiss (2) may still be rejected.

Ancient critics observed, truly enough, that geometrical atomism emasculated their geometry (cf. Xenocrates, fr. 43 H); and they opined that Zeno’s argument was bought off at suicidal expense. Modern critics need not at once concur; for they can propose a subtler version of the atomic objection: physical atomism, they allow, is irrelevant to Zeno’s argument; and Euclidean solids are infinitely divisible. But between physical bodies and geometrical solids lies space. Zeno presupposes that space is infinitely divisible or continuous; i.e., he tacitly assumes that the geometry of space is, in that respect at least, Euclidean. But that assumption is unwarranted; indeed, the moral to be drawn from Zeno’s paradoxes is precisely this: that space (and time) are not continuous.²⁷ Physical bodies have smallest physically separable parts; but that is no serious objection to Zeno. Euclidean geometry allows infinite division to its solids; but that is no help to Zeno. Physical bodies occupy space; and in maintaining that bodies are infinitely divisible, Zeno is maintaining that space is infinitely divisible, that space has no minimal quanta. If we care to reject that assumption, we do not fall foul of geometry: we merely imply that the geometry of space is non-continuous. And we may reject premiss (2).

That sophisticated atomism is a tempting hare; but I shall not indulge in pursuit. For it seems to me that none of the arguments in favour of spatial atomism, and none of the arguments against spatial atomism, is cogent; and I incline to regard the question of the structure of space as an empirical one—to be settled, no doubt, by the abstract theorizings of the physicist rather than by microscopic inspection of pieces of space. If that is right, then we may say at least that Zeno’s proposition (2) is not a truth of logic; but for all that, (2) may be true: it may be a truth of physical theory. And of course, almost all physicists hold that it is true. Further speculation on this topic would be idle: let us grant Zeno (2) and (4).

The second objection to Zeno’s argument attacks proposition (9), his ‘hidden premiss’: ‘(9) proposes a principle for summing infinite series which is simply false; Zeno’s arithmetic was naive, and a sophisticated mathematician will immediately refute his paradox. Z-sets of a are created by dichotomy: the first operation yields {b₁, b₂}, where mag: b_i=½ mag: a; the second operation yields {b₁, c₁, c₂}, where mag: c_i=½ mag: b_i. And so on. Thus the magnitude of the infinite Z-set {b₁, c₁, d₁,…} is equal to ½ mag: a+1/4 mag: a 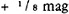: a+…. The infinite series to be summed is:

(S)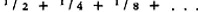

Evidently, the sum of S does not exceed 1; and arithmeticians now make it 1 by definition. Zeno’s infinite series is convergent; and the sum of a convergent series is finite. The principle enunciated in (9) is falsified by the very series Zeno means to apply it to: Zeno’s hidden premiss was accepted by most ancient thinkers, with the honourable exception of Aristotle; but it is tediously false.’²⁸

That objection is horribly confused; rather than anatomize its imperfections I shall show that it is undisturbing to any competent Zenonian. The text of B 1 does, I think, lend plausibility to the claim that Zeno imagined his Z-sets as being generated in the way I have just described; but not all ancient commentators understood the generation in that light. Thus Porphyry restates the argument as follows:

If it is divisible, he²⁹ says, let it be divided in half, and then each of the parts in half. And if this happens in every case, it is clear, he says, that either there will remain some smallest, atomic magnitudes, infinite in number, and the whole will consist of smallest magnitudes infinite in number [sc. and so will be infinitely large], or else it will vanish and be dissolved into nothing and will consist of nothing. And both alternatives are absurd…. (175: Simplicius, in Phys 139, 27–32).

Porphyry’s argument was known to Aristotle (see GC 316a14–34; 325a8–12). Some scholars suppose it to be a Zenonian argument, related to but not identical with the argument of B 1; but Porphyry and Simplicius both treat it as a version of B 1, and I am inclined to take it as an ancient modification or interpretation of our argument.

The important point in Porphyry is this: the dichotomy does not yield Z-sets the magnitudes of whose members form a convergent series; the partitions are ‘through and through’. Each part of a is divided, and every division produces a set whose members are equal in magnitude. Thus the second Z-set of a will not be {b₁, c₁, c₂} but rather {c₁, c₂, c₃, c₄}, where each d has the same magnitude as each of its fellows. Let us define a Z*-set as a Z-set all of whose members are equal in magnitude; and let us replace premiss (4) by:

(4*) If mag: a>0, then there is a Z*-set of a, {x₁, x₂,…} such that for every i mag: xi>0.

Premisses (5) and (7) must be correspondingly emended (the emendation of (7) is trifling, that of (5) more complicated); and the argument will proceed felicitously to (8). To reach (10), we need not

(9) but:

(9*) If S 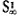is a Z*-set and for every i in S mag: xi>0, then mag: S =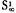

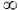
Unlike (9), (9*) is true; for the sum of an infinite series whose members each have the same finite magnitude is indeed, and evidently, infinite. I suppose that those later Greeks who adopted the ‘hidden premiss’ were in fact embracing (9*), on the tacit assumption that the elements to be summed were all of equal magnitude. I doubt if Zeno himself made that assumption; but it is enough that the assumption is readily superadded to his argument, and that the superaddition destroys the arithmetical objection.³⁰

The third objection has Aristotelian roots. According to an Aristotelian dictum, the infinite exists only potentially: potentially, bodies may be divided infinitely often; actually, such a division is impossible. Infinite division cannot be actualized; the dichotomizing always comes to a finite stop; partition ad infinitum cannot be completed. Now Zeno’s argument implies at (4) that infinite division is completable; and it is just there that Zeno goes astray.

Such an objection is worth pondering in connexion with the paradoxes of motion; but here it is readily dismissed. The premisses of the logos on ‘large and small’ contain no reference, explicit or implicit, to any process of dividing: Zeno is not enjoining us to cut, carve or chop up a; nor is he asking us to divide a ‘in thought’. Like Leibniz, he holds that ‘each portion of matter is not only infinitely divisible…but is also actually subdivided without end, each part into further parts’ (Monadology, §65); but he does not say that every body has been, or could be, divided into parts—he asserts that it has parts. He is talking of a characteristic or state of bodies, not of an operation upon bodies. Since Zeno says nothing about dividing, he says nothing about dividing ad infinitum; and reflexions on the possibility of completed divisions are not germane to his argument.

Potentiality, too, is only a toy sword; it is not clear what application that notion has in the context of Zeno’s argument. Aristotle applies his dictum to infinite processes and not to an infinity of parts; the dictum is, in Aristotle at least, a mere ukase; and in any event appropriate injections of the term ‘potentially’ into Zeno’s argument would leave it with its force unimpaired.

The fourth objection comes from Thomas Hobbes. Hobbes had Zeno’s Achilles in mind; but the considerations which led him to reject the Achilles as a ‘sophistical caption’ apply equally to our present argument. Hobbes accuses Zeno of mishandling the concept of infinity: ‘The force of that famous argument of Zeno… consisted in this proposition, whatsoever may be divided into parts, infinite in number, the same is infinite: which he, without doubt, thought to be true, yet nevertheless is false. For to be divided into infinite parts is nothing but to be divided into as many parts as any man will. But it is not necessary that a line should have parts infinite in number, or be infinite, because I can divide and subdivide it as often as I please: for how many parts so ever I make, yet their number is finite’ (De Corpore V.13).

Hobbes appears to vacillate between two objections. On the one hand, he seems to deny that a in fact has infinitely many parts; it has as many parts ‘as you please’, but your pleasure stops short of infinity. If that is his real intention, then he is, in effect, denying the validity of the move from (6) and (7) to (8): the introduction of the sign ‘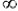’ in (8) is illegitimate. But Hobbes does not explain why this is illegitimate, simply asserting that Zeno argues sophistically.

On the other hand, Hobbes appears to allow that a can be divided into infinitely many parts, but to draw the teeth of his admission by claiming that ‘infinitely many’ here simply means ‘as many as you please’. If that is his real intention, then in effect he allows Zeno to proceed as far as (8) but no further; for on Hobbes’s understanding of ‘infinite’, premiss (9*) is no more true than (9): the sum of as many finite parts as you like need not be infinite. Now Zeno must certainly allow that, given Hobbes’s equation of infinity and the ad lib, premiss (9*) is false; but he is under no obligation to accept the Hobbesian equation. And indeed, that equation is false: there are infinitely many natural numbers; but that is not to say that there are as many numbers as you like; however many you like, there are more (indeed, infinitely many more).

Hobbes, I think, did not grasp the flaw in Zeno’s argument; but his fingers came close to it, and he saw where the argument must be attacked, namely in its handling of the concept of infinity. My fifth and final objection to Zeno owes much to Hobbism; and I preface my remarks with a few elementary reflexions upon the notion of infinity.

It is peculiarly tempting to suppose that the phrase ‘infinitely many’ stands, so to speak, at the very end of the natural number series. If we start counting from 1, the numbers get bigger and bigger, until we pass from the large to the monstrously large, and from the monstrously to the incredibly large—and eventually, if only we went on for ever, we should reach the infinitely large. Thus ‘There are infinitely many Fs’ may seem to have the same logical structure as ‘There are seventeen Fs’; and ‘a can be divided infinitely many times’ is, so to speak, the last member of a series which starts, modestly, with ‘a can be divided once’.

That is all wrong: ‘infinitely many’ does not function like ‘seventeen’; it does not specify a number of Fs or a fixed set of divisions. ‘Infinitely many’ is, on that score, more like ‘as many… as you like’ or ‘more…than you could imagine’. Those latter phrases are not indefinite numerical adjectives like ‘many’ or ‘a lot of’; but nor are they definite in the sense of specifying some particular number. ‘Have as many chestnuts as you like’ does not mean ‘Have lots of chestnuts’, nor ‘Have n chestnuts’ (for some determinate n); rather, it means something like: ‘For any n, if you want n chestnuts, have n chestnuts’.

In a not wholly dissimilar fashion, ‘infinitely many’ is neither an indefinite modifier, like ‘hundreds of’, nor a specifying modifier, like ‘seventeen’. To that extent Hobbes was right. But he erred when he went further and defined ‘infinitely many’ as ‘as many as you please’: the infinite contains as much as you please—and then more; it is inexhaustible, its contents are never used up. To say that a set contains infinitely many members is to say that, however many of its members you have picked out or enumerated, there are still more to count; more precisely, it is to say that for any positive integer n the set contains more than n members. Thus as a first definition of infinity I offer:

(Di) S contains infinitely many members if and only if for every n S contains more than n members.

Now the paradigm of an infinite set is the set of natural numbers or positive integers, {1, 2, 3,….}. However many natural numbers you have taken, more remain; for if you have abstracted k numbers, at least k+1, the successor to k, remains to be abstracted. Pretty clearly, we might use that fact to give a second definition of infinity, viz:

(Dii) S contains infinitely many members if and only if S contains as many members as there are positive integers.

Definition (Di) is not technical; definition (Dii) leaves the infinity of the positive integers unaccounted for; a better definition is sought for. And one can be found (thanks mainly to the work of the German mathematician Dedekind) by way of the notion of a one-to-one correlation. Take any two sets of things, S and S′: a relation, R, will set up a one-to-one correlation between S and S′ if it pairs each member of S with exactly one member of S' and each member of S’ with exactly one member of S. Consider a monogamous society, and let S be the set of husbands and S′ the set of wives. Then the relation of being married to sets up a one-to-one correlation between husbands and wives; for each husband is married to exactly one wife, and every wife has exactly one husband married to her. Again, let S be the set of even positive integers, {2, 4, 6,…}, and S′ the set of positive integers, {1, 2, 3,…}. Then the relation of being double sets up a one-to one correlation between S and S′; for every even positive integer is the double of exactly one positive integer, and every positive integer has exactly one even positive integer that is its double.

The new definition of infinity also requires the notion of a proper subset. That is readily explained: S is a proper subset of S′ if and only if every member of S is a member of S′ and not every member of S′ is a member of S. Thus the set of husbands is a proper subset of the set of married people; for all husbands are married, but not all married people are husbands. And the set of even positive integers is a proper subset of the set of positive integers; for every even positive integer is a positive integer, but not every positive integer is even.

Now we can offer:

(Diii) S has infinitely many members if and only if there is a proper subset of S, S′, and a relation R, such that R sets up a one-to-one correlation between S and S′.

Clearly, the set of natural numbers is infinite by (Diii); for the relation double of will set up a one-to-one correlation between the set of even integers and that set. Hence any set which is infinite by (Di) or (Dii) is infinite by (Diii).

Is any set that is infinite by (Diii) also infinite by (Di) and (Dii)? Suppose that S is infinite by (Diii) but not by (Dii). Then S contains fewer members than there are natural numbers. (I disregard, as irrelevant to Presocratic concerns, the higher infinities or the ‘transfinite’ numbers.) Hence for some k, S contains exactly k members; hence every subset of S contains less than k members; hence no subset of S can be correlated one-to-one with S; hence S is not, after all, infinite by (Diii). Any set infinite by (Diii) is infinite by (Dii), and by (Di); and since (Diii) is precise and explanatory, it is preferable to (Di) and (Dii) as a definition of infinity.

What is all that to Zeno? It helps us to show that Zeno’s argument breaks down at the move from (6) and (7) to (8)—or rather, at the move from (6*) and (7*) to (8). I attempted to ease that move by suggesting that ‘by (6)…there is a Z-set of a 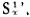, i.e. a Z-set containing infinitely many members. Let us make that into an explicit inference from (6*), thus:

(11*) If a exists, then there is a Z*-set {x1, x2…} of a containing infinitely many xis.

From (7*) and (11*), (8) is validly inferred; but without (11*) Zeno has no way of attaining (8); his argument turns on there being a Z*-set with infinite members.

Yet Zeno has no title to (11*). (11*) does not follow from (6*), nor from any other Zenonian premiss. (6*) does indeed show that a possesses infinitely many Z*-sets: the Z*-sets of a can be placed in one-one correspondence with the natural numbers; and Zeno’s ‘dichotomy’ shows how that is so. But each Z*-set contains finitely many members. Thus let the Z*-sets be generated by successive dichotomies. Then the first Z*-set contains 2 members, the second 4, and so on: in general, the nth Z*-set contains 2n members; and for every n, 2n is finite. There are infinitely many Z*-sets of a. That is to say, for any integer n, there are more than n Z*-sets of a; the Z*-sets of a are as numerous as the integers; certain relations (e.g., having twice as many members as) set up a one-to-one correlation between proper subsets of the set of Z*-sets of a (e.g., the set of Z*-sets whose members are multiples of 4) and the set of Z*-sets itself. There are infinitely many Z*-sets of a. But the number of elements in any Z*-set is finite: for any Z*-set S, there is a natural number k such that there are just k members of S.

It does not follow that no set of parts of a has infinitely many members; indeed, the fact that there are infinitely many Z*-sets of a suggests a way of constructing just such a set. A super-Z-set of a {x1, x2,…} takes x1 from the first Z*-set of a; x2 from the second Z*-set of a, where x2 has no part in common with x1; x3 from the third Z*-set, having no part in common either with x1 or with x2; and so on. Clearly, super-Z-sets will have infinitely many members, since each super-Z-set of a has as many members as there are Z*-sets of a. Equally clearly, super-Z-sets are not Z*-sets; for the members of a super-Z-set are not all equal in magnitude. On the contrary, the magnitudes of members of any super-Z-set form a convergent series: ½, ¼, 1/8…Thus if Zeno were to retreat from Z*- sets to super-Z-sets the traditional arithmetical objection would hold: the sum of the magnitudes of the elements of a super-Z-set is not infinite.

But if Zeno remains with ordinary Z*-sets, his paradox disappears. What follows from his argument about the magnitude of a? Nothing of any interest. By (7) and the principle that if m and n are finite, m +n is finite, we can infer that mag: a is finite. If the Z*-sets are the products of dichotomy, then the magnitude of an element of the nth Z*- set of a will be equal to mag: a/2n. Since the nth Z*-set of a has 2n members, we may conclude, by (7*), that mag: a= 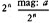And that is an unexciting conclusion to Zeno’s logos.

(f) The totality of things

I turn now to the logos of ‘finite and infinite’, which is contained in sentence [ix] of 175. The logos concludes to the following antinomy: (Z3) (a) If P, then there are finitely many existents, and (b) if P, then
there are infinitely many existents.

The argument for (Z3a) is short: ‘it is necessary that they be as many as they are…But if they are as many as they are, they will be limited’. I paraphrase: ‘If there are many As, then there is some true proposition of the form: ‘There are as many As as Bs”. Hence there is an answer to the question: “How many As are there?” Hence there is some true proposition of the form “There are n As”, where n is a natural number.’

The argument has been called ‘beautiful in its simplicity’,³¹ but it is merely simpliste. Zeno’s final move supposes that a set S is finite if there is a set S′ such that every member of S can be paired uniquely with a member of S′ and vice versa; in other words, if we can set up a one-to-one correlation between S and S′ . But as we have seen, that is not so: the set of even integers can be correlated one-to-one with the set of integers, though both sets are infinite. Zeno’s argument is at once destroyed. Indeed, I find the ‘proof an uninstructive sophism.

The argument for (Z3b) is puzzling: ‘There are always other things in the middle of the things that exist (metaxu tôn ontôn)’. Zeno is usually taken to mean that between any two existents there is always a third. And if Simplicius is reporting Zeno in unabbreviated form, that assertion stood bare of argument. Now between any two points on a line, there is indeed a third; and some scholars take Zeno to be speaking of geometrical points, and thus give his argument a happy gloss. Unfortunately, Zeno’s text does not encourage that interpretation. Others suppose the following train of reasoning: ‘If a and b were contiguous, they would be one object, not two. Hence they must be separated; and since, by Eleatic argument, there cannot be an empty space between them, they must be separated by a third object.’ According to Aristotle, the Pythagoreans said that ‘the void divides nature, the void being a sort of separation and dividing of contiguous things’ (Phys 213b22–7=58 B 30). Perhaps Zeno was implicitly rejecting their view? But that interpretation too requires us to read a great deal into a very plain text.

Perhaps ‘metaxu tôn ontôn’ means not ‘between the things that exist’ but rather ‘in the middle of any existent’. Then ‘there are always other things metaxu tôn ontôn’ means:

(1) For any x, if x exists there exists something distinct from and in the middle of x.

Now Zeno might surely have argued for (1) by appealing to an argument entirely analogous to that in B 1: if a exists, then a has some positive magnitude; and if a has a positive magnitude, then a is divisible into three parts, two ‘outside’ parts and a ‘middle’. Simplicius, I think, took Zeno’s argument in this way; at least, I can think of no other reason why he should have thought that the argument used the ‘dichotomy’. The interpretation is linguistically permissible; and it gives Zeno the conclusion he requires without calling upon any extraneous Eleatic attitudes. Philosophically, of course, this reading of the logos of finite and infinite supplies no food for thought that has not already been digested in considering B 1.

(g) One and many

The fourth logos is the ‘one and many’. Plato mentions it, and we have no reason to doubt that Zeno argued for:

(Z4) (a) If P, then everything is one, and (b) if P, then everything is many.

Zeno’s own words have not survived; nor has any explicit doxographical account of the logos. But we can, I think, reconstruct at least part of Zeno’s argument on the basis of some remarks of Simplicius and Philoponus.³² The remarks go back to Eudemus, who gives the closest approximation to (Z4) that we possess:

Zeno, the friend of Parmenides, tried to prove that it is not possible for what exists to be many because [i] nothing among the things that exist is one, and [ii] the many are a quantity of ones (plêtbos henadôn)³³ (178: fr. 37aW=A 21).

Here [i], I take it, derives from (Z4b), [ii] from (Z4a).³⁴

For (Z4b) we may again call upon Eudemus. Having retailed the anecdote of Zeno and the One (above, p. 235), he continues:

He was puzzled, as it seems, by the fact that each of the perceptible things is called many both by way of predication (katêgorikôs)³⁵ and by partition, while the point cannot even be posited as one (for what neither increases when added nor diminishes when subtracted he thought not to be an existent)…. But if points are of that character, and each of us is said to be many things (e.g., white, musical, etc.) and similarly with a stone (for each one can be infinitely split), how will there be any one? (179: fr. 37aW=Simplicius, in Phys 97.13–21; cf. A 21).

Eudemus’ argument runs as follows: ‘If there are many things, each is either [a] a perceptible object or [b] a point. If [b], then the object has no existence, and a fortiori is not “one” thing. If [a] then [i] the object is infinitely divisible and so is “many” not one; and [ii] the object, having many predicates true of it, is “many” not one.’

Eudemus’ reconstruction is his own: he is not pretending to report an argument of Zeno’s, but to discover why he should have been puzzled by ‘the One’. But Eudemus bases himself firmly on Zenonian soil: [b] comes from B 2, and [a] [i] repeats the familiar move of B 1. [a] [ii] is a novelty to us; but I think we are entitled to trust Eudemus and to regard it too as Zenonian; and I suppose that it constituted Zeno’s argument for (Z4b).³⁶

The argument rests on the truism that everything has more than one property: Socrates is both pale and snub-nosed; Socrates possesses the property of pallor and also the distinct property of snubnosedness. In general:

(1) (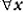) ()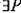. () (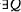P is distinct from Q, and x has P, and x has Q). How did Zeno infer from (1) that ‘everything is many’?

Most of the commentators suppose that he indulged in a naive and archaic confusion: muddling together predication and identity, Zeno managed to construe ‘Socrates has pallor’ as though it were ‘Socrates is pallor’; and he thus read (1) as though it were:

(2) (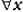) () (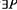)(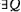P is distinct from Q, and x=P and x=Q). Given (2) we can see how ‘everything is many’; for everything is identical with at least two distinct things.

The confusion which encourages us to move from (1) to (2) was not unknown to the Greeks. According to Aristotle, in order to avoid the paradox of ‘one and many’ ‘some did away with “is” (e.g., Lycophron), and others emended the language, saying that the man (not is pale but) has paled, and (not is walking but) walks’ (Phys 185b27–30=83 A 2). Aristotle reports a diagnosis and a prophylactic. The diagnosis has it that our confusion between identity and predication is brought about by the word ‘is’: if we take ‘Socrates is the Chairman’ to assert an identity between Socrates and the Chairman, we may be seduced into taking ‘Socrates is pale’ to assert an identity between Socrates and pallor. The prophylactic is simple: abolish ‘is’; instead of’Socrates is pale’ write ‘Socrates pale’ or ‘Socrates has paled’.

The ‘paradox’ which worried Lycophron and the others seems trifling to us; but it clearly seemed serious to Zeno’s contemporaries, and we may well imagine that (Z4b) trades upon it. (Note that Eudemus reported Zeno’s argument in his Physics: Eudemus’ Physics corresponds closely to Aristotle’s, and the Eudemian fragment happens to answer to Phys 185b27–30.) For all that, I am not entirely happy in ascribing (2) to Zeno: (2) is contradictory in itself (for if x= P and x=Q, then P=Q), and therefore not an ideal component in an antinomy. At all events, it is worth casting about for an alternative interpretation.

Let us return to Eudemus. According to him, ‘Plato thought that “is” [sc. in “Socrates is pale”] does not signify what it does in the case of man, but that just as “is thoughtful” signifies to think and “is seated” to sit, so it is in the other cases too, even if there are no ready-made names for them’ (fr. 37aW=Simplicius, in Phys 97.25–8). Plato’s answer to a puzzle of predication distinguished, in effect, between the ‘is’ of essential and the ‘is’ of accidental predication. If that answer was appropriate, then it suggests a paradox about essence, rather than one about identity: ‘[a] Each thing is just one thing, i.e., has a unique essence, [b] If a has P, then having P is what a is; i.e., is the essence of a. Hence, by (1), each thing has more than one essence or is many. ‘If that Platonic puzzle seems anachronistic, let me double the offence by adverting to a peculiarly Aristotelian concern: the unity of definition. Thus: ‘[a] Each thing is a unity, [b] If a has P and Q, and having P does not involve having Q, nor vice versa, then a is a diversity; hence by (1), a is a diversity or “many”.’³⁷

These three diagnoses of Zeno’s problem, the traditional one, the Platonic, the Aristotelian, are all unsatisfactory in one way or another; and it may be that no precise interpretation is possible. In his paradox of ‘one and many’, Zeno raised, in a vague and indeterminate fashion, several issues that were to excite and perplex his successors; he himself merely saw, or imagined, a conflict between ‘being one’ and ‘being many’, which properties all objects surely possess. It was left to Zeno’s successors to distinguish particular knots in that tangled skein, and to pose plain puzzles to the adherents of pluralism. But note, again, that pluralism is not peculiarly vulnerable to this antinomy: Zeno’s arguments, however they are elucidated, work whether a is a member of a numerous plurality or the sole inhabitant of the world: the ‘one and many’ is an antinomy of being, not a paradox of plurality.

(h) The paradox of place

I shall end the chapter by looking at two minor arguments which seem only loosely connected with the main theme of Zeno’s logoi. These arguments are the paradox of place, and the paradox of the millet seed.

The paradox of place is twice adverted to by Aristotle (Phys 209a23; 210b22=A 24=13–14 L), and it is discussed by Aristotle’s commentators. Zeno’s actual words do not survive; but an argument in Simplicius (in Phys 563.1–33) persuades me that the closest approximation to authenticity is achieved by Philoponus:

For if everything that exists is somewhere, he used to say, and place too is something, then place too will be somewhere. Hence place will be in a place; and so ad infinitum (180: Philoponus, in Phys 510.4–6=16 L; cf. Simplicius, in Phys 534.6–15).³⁸

Zeno’s immediate conclusion was, presumably, that there is no such thing as place. Conceivably, he then inferred that existent things are not in any place, and aimed to construct an antinomy:

(Z5) (a) If P, then everything is somewhere; and (b) if P, then everything is nowhere. Here (Z5b) is the ultimate conclusion of the paradox of place; and (Z5a) will have been inferred along the lines of B 2: if a exists, it has magnitude; if it has magnitude, it is spatially extended; hence it is ‘somewhere’.³⁹ (Note again that in (Z5) the pluralist hypothesis is idle.)

The kernel of Zeno’s argument is his assertion that everything that exists is ‘somewhere’ or occupies some place:

(1) If a exists, then for some x a occupies x.

The second premiss, that ‘place too is something’, may be construed as:

(2) If a occupies b, then b exists.

From (1) and (2) Zeno hopes to generate an infinite regress of places. Let us make the innocuous assumption that the relation of occupation is irreflexive, asymmetrical, and transitive; i.e., that:

(3) Nothing occupies itself.

(4) If a occupies b, b does not occupy a.

(5) If a occupies b and b occupies c, then a occupies c.

Now it is easy to prove from (1)—(5) that any existent body occupies infinitely many distinct places:

(6) If a exists, then for any n there are more than n distinct places occupied by a.

According to Zeno, (6) is absurd; hence (Z5b).

Is (6) absurd? Well, how can places be distinct other than by having distinct boundaries? And how can one and the same object, a, have more than one set of boundaries?

If (6) is unacceptable, does Zeno’s argument for it fail? The ancient critics attack (1). According to Aristotle, the term ‘occupy’ is ambiguous: everything must indeed be ‘in’ something, but not all ways of being ‘in’ a thing are cases of occupying a place. Heat, say, is ‘in’ a body; but the body is a substrate, not a place, for heat (Phys 210b22–30). Thus (1) does not state any one truth because it does not state any one thing at all; and if it is made explicit that occupation in (1) is a matter of being in a place, then (1) is false, as Eudemus says: ‘now if [Zeno] assumes that what exists is in a place, his assumption is incorrect; for neither health nor courage nor ten thousand other things would be said to be in a place’ (fr. 78 W=A 24).⁴⁰

I am, I confess, inclined to side with Zeno here, and to support some version of (1): if existents need not occupy places, then they exist in so far as they are related to some place holder, and they exist only in a derivative sense. But it is unnecessary to develop that line of thought here; for (1) is easily repaired against the Aristotelian attack. Zeno need only restrict a and b in (1) and (2) to things of a sort capable of being located in space; for surely anything that can occupy a place exists only so long as it actually does occupy a place. Premiss (1) then asserts, uncontroversially, that any potential occupant of space does, if it exists, actually occupy a place.

Premiss (1) is true. Is (2) false? If (2) is true, then places are themselves capable of being located. It might be said that an object a occupies a place p if and only if the coordinates defining p determine the surfaces of a; and since places do not have surfaces, they are not locatable in space. But that is pedantry; why should we not say that a place p occupies a place p′ if and only if the co-ordinates of p′ determine the co-ordinates of p? In general, a occupies b if and only if the determining co-ordinates of a are the same as those of b. Necessarily, places have places: (2) is necessarily true. But the truth of (2) is bought at a price. For on that account of occupation, (3) and (4) are both false: occupation is neither irreflexive nor asymmetrical; for places are their own locations. As Newton put it: Times and spaces are, as it were, the places as well of themselves as of all other things’.

I do not insist on the Newtonian answer; for nothing, I think, hangs upon it. Some will accept Zeno’s (1) and (2), rejecting (3) and (4). Others may prefer a weaker notion of existence, and deny (1); yet others will contrive reasonable grounds for rejecting (2). Zeno’s argument certainly fails: it is interesting to observe that it fails even if we grant Zeno both of his explicit premisses.

(i) The millet seed

The paradox of the millet seed is reported by Simplicius:

In this way [Aristotle] solves the problem which Zeno the Eleatic set for Protagoras the Sophist. ‘Tell me, Protagoras,’ he said, ‘does a single millet seed make a sound when it falls? Or the ten thousandth part of a seed?’ Protagoras said that it didn’t. ‘What about a bushel of millet seed’, he said, ‘does that make a sound when it falls, or not?’ He said that the bushel did make a sound. ‘Well’, said Zeno, ‘isn’t there a ratio between the bushel and the single seed, or the ten-thousandth part of a single seed?’ He agreed. ‘Well then,’ said Zeno, ‘won’t the sounds too stand in the same ratios to one another? For as the sounders are, so are the sounds. And if that’s so, then if the bushel makes a sound, the single seed and the ten-thousandth part of a seed will make a sound too’ (181: A 29=38 L).

Simplicius is reporting a later dramatization of the paradox; but Aristotle’s testimony ensures that the argument itself is genuinely Zenonian (Phys 250a19=A 29=37 L).

The argument is sometimes supposed to be an attack on sense-perception: reason proves the millet seed to make a sound, even though our ears detect none. Archytas later asserted, conceivably with Zeno’s millet seed in mind, that ‘many sounds are not apprehensible by creatures of our nature, some because of the weakness of the blow [which produces them], others…’ (47 B 1). The millet seed might, I suppose, illustrate a problem in the philosophy of perception; yet interest in such problems is not Eleatic. Nor will the millet seed argue for an Eleatic scepticism: at most it might persuade us of the uncontroversial fact that many things elude our perception even though they are intrinsically perceptible.

Imagine that one of Zeno’s forty logoi aimed to prove:

(Z6) (a) If P, then each existent makes a sound, and (b) if P, then each existent is mute.

The millet seed argues for (Z6a); and we might easily concoct an inverted version of the same argument to support (Z6b). The suggestion is purely speculative and not worth developing; but the millet seed itself warrants another page.

The Megarian philosophers of the early fourth century, who are often spoken of as the successors to the Eleatic school, invented a series of logical puzzles. Two of them, the heap (sôreitês) and the bald man (phalakros) are near cousins to the millet seed. One grain of sand is not a heap, and the addition of one grain cannot turn what is not a heap into a heap; a man with a full head of hair is not bald, and the extraction of a single hair cannot make what is not bald bald: hence there are no heaps, and no bald men. The puzzles are jocular but the point they make is serious. They seem to provide counterexamples to the powerful logical tool of mathematical induction. The general formula for such an induction is this: Take an ordered sequence <a₁, a₂,…, a_n,…>; if a₁, is F, and if, if a_n is F then 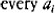is F, then every ai is F. The millet seed and the Megarian puzzles can be formulated as mathematical inductions: the ais are bags of millet seed, each ai containing exactly i seeds; and for ‘F’ read ‘makes no audible sound on falling to the ground’. The conclusion, that every ai is F, states the absurdity that no amount of millet seed makes a noise on falling.

It is often said that puzzles of this sort essentially use ‘vague’ concepts; and the moral is drawn that precise logical manoeuvres, such as mathematical induction, do not work for vague concepts. We might accept that and still worry about the Megarian puzzles: first, have they not shown a decisive logical flaw in such common notions as those of ‘a heap’ and of ‘baldness’? And second, how are we to define the conditions a concept must satisfy if it is to be amenable to precise logical deployment?

Consideration of the millet seed thus opens some fairly large questions about the connexion between formal logic and ordinary language. Yet I am not sure that Zeno’s paradox depends for its solution on an answer to those questions. After all, the predicate ‘makes an audible sound’ is not particularly vague: either I can hear the seed or I cannot; there is no halfway house between hearing and not hearing, in the way in which there seems to be between being bald and not being bald. Aristotle offers an answer to Zeno which in no way turns on the notion of vagueness: in effect, he challenges Zeno’s implicit claim that if an makes no sound, then an+1 makes no sound (cf. Phys 250a9–28). There is, for each of us, a threshold of audibility: the addition of a single seed to a parcel of millet may indeed make all the difference between audibility and inaudibility—even though that seed, falling alone, is not audible. Zeno, according to Aristotle, supposes that if n grains make a sound of volume V, that can only be because each grain makes a sound of volume V/n. And that assumption, which is not a logical but an empirical proposition, is false. Aristotle’s diagnosis of Zeno’s error, and his answer to Zeno’s puzzle, seem to me to be correct.